Impact of vibrations to the human fatigue and manual assembly performance

1. Introduction

Production system efficiency is the main indicator defining the performance of the manufacturing company. Even some advanced manufacturing systems omits efficiency as the main criteria [1], the majority of manufacturing companies, especially in the automotive industry perceive efficiency as the major competitiveness factor. Therefore, companies apply a lot of measures to increase the efficiency. In general, manufacturing system efficiency is based on a many different factors. Many manufacturing companies apply robotic and other automatic equipment for production processes, thus efficiency becomes based on maintenance of this equipment, planning of operations and etc. In such a process operators control the process and improve the efficiency only indirectly. On the other hand, still there are many industries where manual assembly is being performed by operators at the assembly lines and working cells. In such companies, efficiency is mostly based on worker operational performance, i.e. time of the manual assembly operations. Manual assembly time of the operators is based on variety of factors such as motivation, working skills, working environment, quality of tools, work organization and ergonomic aspects.

Human factors and ergonomics encompass many different aspects such as workplace pollution, mechanical oscillations and vibrations, noise, lightning, work posture, workplace design and etc. These subjects are widely studied by a scientific researchers and practitioners [2, 3]. Also it is reported, that good ergonomic situation leads to increased productivity and profit [4]. Many ergonomic factors can be quite easily provided to make work place safe and comfortable, but regarding manual and semi-automatic assembly, the most dangerous factors for the operator health remain vibrations and repetitive motions, due to the fact that they directly affect operator body and its parts [5]. What is more, a global competition in the manufacturing industries demands for an increased production capacity and lower production costs. Thus assembly operators receive increased work rate i.e. they are required to produce more during the same period of time or/and are forced to work overtime to complete production orders. Gooyers and Stevenson [6] reported that an increased work rates demand for increased muscular effort which leads to elevated risk of musculoskeletal injury. Companies competing for each customer order often omit the most important ergonomic factors and then they are forced to pay compensation costs for employees for damaged health and work related traumas [7]. On the other hand, many authors claim [2, 3, 5, 8, 9] that traumas caused by vibrations and repetitive motions can be avoided if they are measured and correctly distributed between assembly operators, although there are still lack of accurate measurement tools and models to evaluate the risk of vibrations for the operator health and especially operation time.

In this paper the mathematical model interconnecting exposure to vibrations and manual assembly time is presented. Presented model enables to monitor operational improvement and to predict an assembly time increment and ultimate operator disability to perform the manual assembly task. In order to evaluate and prove the adequacy of proposed model the model was tested on a production data from the manufacturer performing manual assembly of the automotive wiring harnesses. This manufacturer is encountering major global marked challenges for cost reduction; therefore, the operational efficiency is the major factor defining company’s competitiveness. This situation results increased working rates, increased working time (operators have to work overtime in order to complete deliveries on time) and finally leads to boosted occurrence of hand-arm vibration syndrome. A specific product with vibration press used in assembly was selected form company’s environment. Appropriate tool vibration and human health measurements were performed.

2. Implications of vibrations and repetitive motions on human performance – a review

In the manual assembly process due to the fact, that parts and components of assembly need to be manipulated and variety of hand tools should be applied, two major risk factors exist: segmental vibrations and repetitive motion injuries (RMI) or cumulative trauma disorders (CDT) [3]. In the most cases these two risk factors both affect human body simultaneously and both lead to the same injuries and professional diseases.

In manual assembly segmental vibration occurs for the operators which manipulate the power tools by hands such as drills saws, heaters, hammers and similar equipment which vibrate and transmit the vibration to hand [5]. The most common injury in such case is white finger disease. This disease occurs due to prolonged usage of hand tools vibrating at 20-100 Hz frequency. Such tools include the major power tools (drills, impact wrenches and etc.). If such a vibration continues, this leads to permanent damage of nerves and blood vessels in the hand [3]. A prolonged segmental vibration also leads to other injuries such as hand-arm vibration syndrome and carpal tunnel syndrome [10]. Regarding the manual assembly performance this mean temporal or even permanent impairment of hand functions.

RMI and CTD are being widely recognized in manufacturing ergonomics for last 30 years [2, 7, 11, 12] and they come as a result from these operational activities [3]: repetitive hand movements with high force; flexion and extension of hand; high force pinch grip.

The particular operations causing these factors include: grinding, working with press, assembly of small components (wrapping, wiring etc.), belt conveyor assembly, packing operations and etc. To sum up, these operations encompass the most of activities performed in the manual assembly especially in high volume production and if repetitive motions continue for a longer time interval they lead to CTD. The major RMI are carpal tunnel syndrome, cubital tunnel syndrome and tenosynovitis. More specific RMI and CTD can be found in scientific literature [2, 3, 11]. The symptoms of these RMI include numbness, inflammation of tendons, swelling and similar injuries that prevent operator from working.

The significance of repetitive motions and vibration effects to human work is reported by many researchers. The major parameter defining the risk of vibrations and CTD is time on which exposure to risk factors lasts. Therefore, there are plenty of calculation methods available to measure an optimal exposure time to risk factors [13-16]; however, most of them suffer from uncertainty and accuracy problems and some recent research address this issue [17, 18]. It is not enough to solely know that vibration effects human work, it is also important to measure direct impact of risk factors to assembly time of the operator. Therefore, the main idea of this research is to connect the vibration caused disorders with the human performance in terms of processing time.

3. Vibration used in manual assembly and its effect on human health

A specific product with vibration press used in assembly was selected form company’s environment. This product has high volumes (up to 35000 per year) and is being mass produced in the certain production department by manual assembly operators. This particular product is the vehicle’s windshield washer nozzles for heated system. Typical example of such wiring harness product is depicted in Fig. 1.

Fig. 1Windshield washer nozzles for heated system

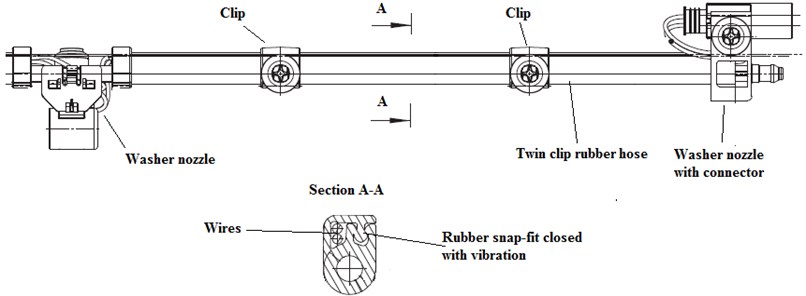
The product assembly constitutes of certain standard operations. Some of these operations have no risk for an operator health (inserting of wires, assembly of connector, nozzles, clips and etc.). In addition to this, during the assembly of this product, the hand manipulated vibrating press is used to close the snap-fit connection along twin hose after the insertion of wires. This operation is depicted in Fig. 2.

Fig. 2Assembly with vibrating press

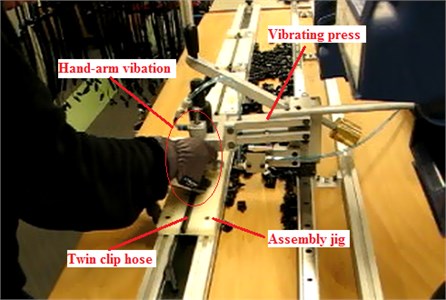
During the assembly twin clip hoses of the washer nozzle system are placed onto the assembly jig. Manually manipulated moving vibrating press is applied and dragged along the whole length of the washer nozzle system to close the twin clip hose to secure wires inserted inside. The total assembly time of the product is 1.75 min and 0.8 min is dedicated for the working with vibrating press only. This is significant number and also it can be concluded that the half of the assembly time causes hand-arm vibration and results risk to the operator health.

In order to evaluate impact of the vibrations to the human operator via hand-arm vibration, vibrations of the tool (vibrating press) were measured. The results are represented in Fig. 3.

Fig. 3Vibration measurements of the vibrating press

Graphical representation of spectral analysis is presented in Fig. 4. Spectral analysis shows that vibration frequency is almost constant and equals to 66.67±2 Hz and average of the amplitude is 0.5 mm. These values indicate that this press exposes the working operator to the risk [5].

Fig. 4Spectral analysis of vibration

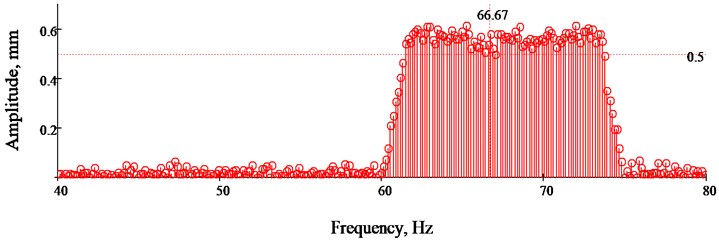
Fig. 5Measured production data

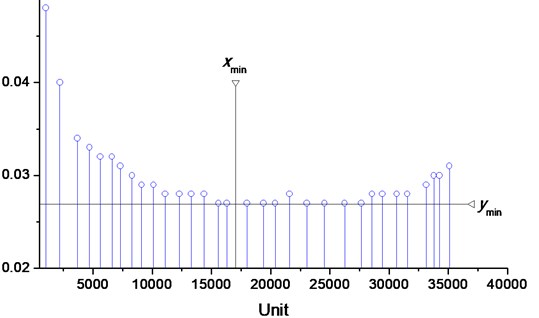
The production data monitoring was performed in the particular assembly department where operators assemble several different products in high volume. Need to emphasize that in this particular department are working only unqualified assembly operators. The production time was monitored for a year period. In the most of the cases monitored assembly time after initial improvement, starts to climb up as the assembly operation continues.

Please note that many different measurements were performed i.e. many statistical data collected and then summarized to one average data set. The data analysis show that there is a certain breaking point, which denotes the end of the performance progress, i.e. there exist a certain number of the production cycle $x_{\mathrm{m}\mathrm{i}\mathrm{n}}$ in which the minimal assembly time $y_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is reached. (see Fig. 5).

To evaluate the status of the human body, heart rate variability (HRV) measurements were performed as well. During the learning process when healthy operator is performing manual assembly tasks HRV measurements show normal HRV. After the clear indications that human working time starts to decrease (this indication is pictured from the production data monitoring), measurements indicate abnormal HRV. These findings in the change of HRV diagrams proposed the idea that there is a certain breaking point of the operator’s health state and this breaking point corresponds to the assembly time progress breaking point (i.e. worker is already at the state of slight illness). Therefore, additional measurements were performed addressing the very point of this health state and assembly time change. Summarizing many different statistical measurements ultimate result was disclosed that indeed this point actually exists. This point is presented in Fig. 6.

Fig. 6HRV respect to produced parts

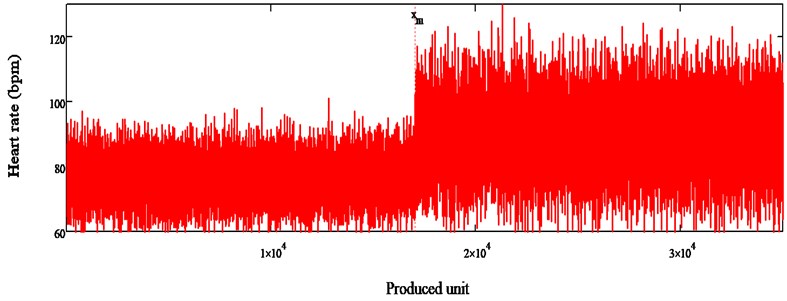
Since this point corresponds to the assembly time breaking point, the minimal assembly time $y_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and the certain product number $x_{\mathrm{m}\mathrm{i}\mathrm{n}}$ can be determined form the production data measurements.

4. Proposed analytical model to analyze manual assembly time

The well-known method in the manual assembly to analyze production time improvement is the learning curve [19]. Learning curve (in this article classical learning curve (CLC)) shows time decrement as the argument (number of units) increases. However, CLC cannot encompass any risk factors, due to the fact that it is monotonously decreasing function. In order to include vibration exposure to the learning curve CLC must be treated as solution of the differential equation. Since the CLC [19] is defined as $y(x,\alpha ,\beta )=\beta x^{-\alpha }$, $\beta >0$,$\mathrm{}0<\alpha <1$, $x\ge \text{1}$ CLC is the solution of Cauchy problem:

where $L_{\alpha }\left[y\right]=y\mathrm{\text{'}}+\alpha x^{-1}y$. Let the solution:

of the problem Eq. (1) be a definition of CLC. Let as consider the more general Cauchy problem:

which solution is:

then $\beta =y(1,\alpha )$. All classical learning curves [19] satisfy following properties:

Obviously, the bundle Eq. (4) (with respect to $\alpha$) satisfies properties Eqs. (5)-(7).

To connect assembly time and exposure to vibrations a small additive fraction of time to define injury development to each repetitive cycle should be added. Thus assembly time decreases as the learning phase is completed, but starts to climb up slightly as the injury starts to develop due to exposure to vibrations and repetitive motions. Let us analyze Cauchy problem with small perturbation parameter (injury development):

and its solution:

where $s(x_1,w_1,\alpha ,\epsilon )=x_1^{\alpha }\left[(1+\alpha )w_1-\epsilon x_1\right]$.

We will state sufficient conditions for parameters $\alpha$, $\epsilon$, $x_1$ and $y_1$ such that solution Eq. (9) satisfy Eq. (5) and:

Such solutions are called the ALC [20]. Note that under conditions $x\in [1,+\mathrm{\infty })$, $\alpha \in \left(\mathrm{0,1}\right)$ and $\epsilon \in (0,+\mathrm{\infty })$ the solution Eq. (9) exists and is unique [21], because $\alpha /x$, $\epsilon /x\in C^{\left(0\right)}[1,+\mathrm{\infty })$.

Proposition. Under the conditions:

the solution Eq. (9) of Cauchy problem Eq. (8) satisfies conditions Eq. (5), Eqs. (10)-(12).

Proof. Under the conditions Eq. (13) number $s(x_1,w_1,\alpha ,\epsilon )>0$ and the function $w(x,x_1,w_1,\alpha ,\epsilon )>0$, hence the second derivative:

i.e. solution Eq. (9) is a positive and convex function:

is strictly monotone increasing and equation:

have a unique solution:

hence minimum time for the $x_{\mathrm{m}\mathrm{i}\mathrm{n}}$ cycle is:

In this way we proved that positive and convex solution Eq. (9) is a unimodal function and reaches its minimum at the point $x_{\mathrm{m}\mathrm{i}\mathrm{n}}\in (1,\mathrm{\infty })$. If $x_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is known, then the dependency of $\epsilon$ on $\alpha$ follows from Eq. (15) and Eq. (17):

and the separate dependency of $\epsilon$ on $\alpha$ follows from Eq. (9) and Eq. (16):

After inserting Eq. (19) to Eq. (20) equation for parameter $\alpha$ is derived:

Let the solution of Eq. (21) is ${\alpha }_0$, then the parameter ${\epsilon }_0=\epsilon \left({\alpha }_0\right)$. Therefore, the solution of Eq. (8) $w=w(x,x_1,w_1,{\alpha }_0,{\epsilon }_0)$ is unique, if the additional condition $w_x^{\text{'}}(x_{\mathrm{m}\mathrm{i}\mathrm{n}},x_1,w_1,\alpha ,\epsilon )=0$ is satisfied.

Now, the proposed ALC model is applied to the measured production data from Fig. 5. Monitored production data is presented in such a form:

where $x^{\left(i\right)}$ is number of unit, $y^{\left(i\right)}$ is processing time of the $x\text{th}$ unit. Let ${\mathbf{W}}_{cal}=\left(w(x^{\left(1\right)},x_1,w_1,\alpha ,\epsilon ),...,w(x^{\left(N\right)},x_1,w_1,\alpha ,\epsilon )\right)$ are recovered results by using ALC model Eq. (8) and Eq. (9).

With the known parameters minimum point ($x_{\mathrm{m}\mathrm{i}\mathrm{n}}$, $y_{\mathrm{m}\mathrm{i}\mathrm{n}}$) and initial condition for Cauchy problem ($x_1$, $y_1$) the Eq. (8) is solved and the solution is unique (as it is proved). Then the ALC model is fully defined. The accuracy of the production data approximation is measured by norm ${\delta }_{abs}=‖{\mathbf{W}}_{cal}-\mathbf{W}‖$ and relative norm [22] ${\delta }_{rel}=‖{\mathbf{W}}_{cal}-\mathbf{W}‖/‖{\mathbf{W}}_{cal}‖$, where:

is Hilbert-Schmidt norm.

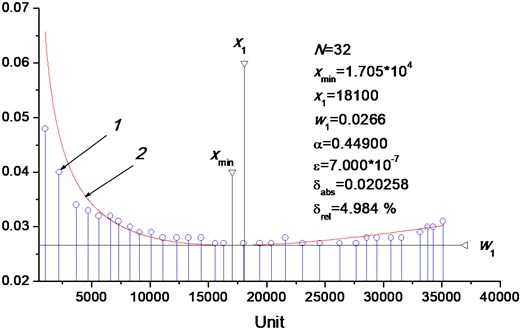
It is clear from the graph in the Fig. 7 that ALC approximates manual assembly performance quite accurately. The relative error is quite small, only 4.98 %. What is more, analytical calculation confirms that there is a minimal assembly time after which, operator improves no more due to injury development. Moreover, if the manual assembly with vibration used is considered, by using determined model, the assembly time decrement and injury development can be predicted from the initial production data. This can be practically applied to the manufacturing situations to prevent hand-arm vibration syndrome by worker rotation.

Fig. 7Production data and ALC for performance prediction. 1 – monitored production data, 2 – function calculated by Eq. (8)

5. Conclusions

In this paper the manual assembly with vibrating press used is considered. Production time monitoring and operator health state analysis by HRV measurements were performed. These measurement indicates that there exists a minimum point after with human performance starts to decline due to development of hand-arm vibration syndrome. This data was further used for mathematical analysis to develop mathematical model for assembly time development.

The mathematical model based on almost learning curves as the solutions of perturbed differential equation is presented. These solutions give relationship between operation times and number of produced units. Perturbation parameter represents the impact of the vibrations to human performance in the learning curve. Application results show that the proposed model approximates manual assembly time development quite accurately, the relative error is quite small, i.e. 4.98 %.

Proposed model has a unique practical importance since in enables to predict occurrence of hand-arm vibration syndrome and prevent it before it starts to effect human health.