Parameters identification of a cannon counter-recoil mechanism based on PSO and interval analysis theory

2.1. Mathematical model

An manual recoil motion was carried out on the counter-recoil mechanism of the cannon. After the manual recoil motion, the recoiling parts of the cannon return to the in-battery position under the action of the force from the recuperator. According to working principle of counter-recoil mechanism, the forces from the recuperator and recoil brake can be expressed as follows:

The motion differential equation of cannon recoil process is:

In Eqs. (1-3), $F_f$ is the recuperator force, $F_z$ is recoil brake force, $x$ is the recoil displacement of the cannon, $u$ is the recoil velocity, $\lambda$ is the maximum recoil length, $P_{f0}$ is the initial pressure of the recuperator, $n$ is the gas nonlinear exponential of the recuperator, $k_1$ is the main stream hydraulic resistance coefficient of recoil brake, $k_2$ is the tributary hydraulic resistance coefficient of recoil brake, $a_x$ is the area of flow hole, $A_f$ is the piston working area of the recuperator, $A_{fi}$ is the gauge working area of the recuperator, $a_f$ is the groove area, $D_T$ is the inner diameter of the drawing cylinder, $d_T$ is the outer diameter of the drawing cylinder.

2.2. Parameter classification of the counter-recoil mechanism

According to the mathematical model established above, there are many parameters in the counter-recoil mechanism which can be divided into three types. (a) The first type contains the parameters that are certain and can be determined by calculating or measuring. (b) The second type contains parameters that are unknown or hard to be measured. However, they are certain during a certain action cycle due to the short time of the cycle. This type of parameters can be obtained by identification methods. The two unknown parameters need to be identified in this paper are the initial pressure $P_{f0}$ and the gas nonlinear exponential $n$ of the recuperator. (c) The third type contains parameters that are uncertain, and the true values of this type parameters are changing even in a certain action cycle. The present cognitive means can only determine the range of the third type of parameters instead of an exact value or the definite distribution rules. The two interval uncertain parameters are the mainstream hydraulic resistance coefficient of $k_1$ and the tributary hydraulic resistance coefficient $k_2$ of recoil brake.

In order to identify the second and third type parameters above, the entire identification process is divided into two parts. First, identifying $P_{f0}$ and $n$ when the uncertain parameters $k_1$ and $k_2$ are changing in their interval ranges. Then, identifying the uncertain parameters $k_1$ and $k_2$ after determining the values of $P_{f0}$ and $n$.

3.1. Description of the identification problem

The parameters identification problem of the recuperator can be solved by regarding it as an optimization problem: seeking out an optimum $P_{f0}$ and $n$ that make the outputs of the mathematic model agree best with the objective function when the uncertain parameters $k_1$ and $k_2$ are changing in their interval ranges. The mathematical model is expected as follows:

where, $\mathbf{X}$ is the unknown vector that need to be identified, $\mathbf{X}=(P_{f0},n)$. $\mathbf{D}$ is the uncertain vector, $\mathbf{D}=(k_1,k_2)$. $f$ is the objective function. Because the possible values of $\mathbf{D}$ constitute an interval, the results of the objective function is an interval number. In this paper, the interval uncertain identification was turned to a certain optimization problem by interval sequence conversion model, and PSO algorithm was proposed to identify the parameters.

Interval sequence relation is used to evaluate the interval numbers quality. According to the interval number theory, an interval number can be denoted by midpoint $A^c$ and radius $A^w$:

We expect to seek the best unknown parameters that can make the objective function has the largest midpoint and radius. First, the optimization problem with uncertain interval expressed by Eq. (4) is converted into a certain optimization problem. Then, with the linear weighting method, transforming it into a certain single-objective optimization problem [3]:

where, $f_d$ is the single-objective evaluation function, $\beta$ is the weight value with range [0, 1], $\xi$ is a parameter to ensure that $f^c\left(\mathbf{X}\right)+\xi$ and $f^w\left(\mathbf{X}\right)+\xi$ are nonnegative, here $\xi =0$ due to the nonnegative similarity degree. $\varphi$ and $\psi$ are regularization factors of the multi-objective function, they can be obtained by Eq. (7):

Fig. 1Sensor installation figure

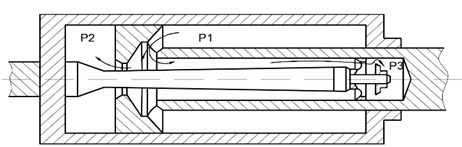
Fig. 2Recoil brake structure and pressure test chamber figure

In this paper, the similarity degree of the time-series data is used to evaluate the identification results. The objective function is the similarity degree $S$ between the simulated curve or test curve and identification curve and it is comprised of the numerical similarity $S_1$ and the shape similarity $S_2$. The range of $S$ is [0, 1], $S=$0 denotes that the two systems are completely alien, $S=$1 denotes that the two systems are identical, and $0<S<1$ denotes the level of similarity of the two systems [4]. According to multi-attribute and multi-index synthesis theory, when calculating the similarity degree, it is better to use multiplication relation than addition relation between numerical similarity and shape similarity [5]. The numerical similarity is represented by the weighted average of the relative errors and the shape similarity is evaluated by landmark dividing method.

The simulated curve is the pressure of chamber P3 in the recoil brake and it is obtained by virtual model simulation while the test curve is obtained during the manual recoil process using a piezoresistive pressure sensor PN3000.

3.2. Parameters identification results

The unknown parameters of the counter-recoil mechanism are identified by PSO in this paper [6]. During the identification process, the parameters of PSO are as follows: the population size is 50, the maximum iteration step is 80, $c_1=\text{1.2}$, $c_2=\text{1.7}$, and the inertia weight $\delta$ is linearly decreasing, $\delta \left(k\right)={\delta }_{\mathrm{m}\mathrm{i}\mathrm{n}}+({\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\delta }_{\mathrm{m}\mathrm{i}\mathrm{n}})(T_{\mathrm{m}\mathrm{a}\mathrm{x}}-k)/T_{\mathrm{m}\mathrm{a}\mathrm{x}}$, where $k$ is the current iteration step, $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum iteration step, ${\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}=\text{0.9}$,${\delta }_{\mathrm{m}\mathrm{i}\mathrm{n}}=\text{0.4}$. The range of the parameters needed to be identified are as follows: the range of the initial pressure of counter-recoil mechanism $P_{f0}$ is [2.08, 3.12], and the gas nonlinear exponential of counter-recoil mechanism $n$ is [1.04, 1.56]. The range of the uncertain parameters $k_1$ and $k_2$ are [1.2, 1.76] and [1.8, 2.64].

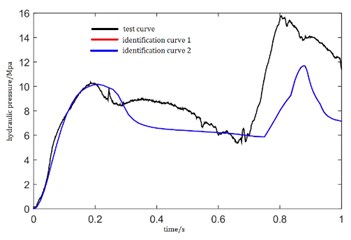
Table 1 and Table 2 give the identification results of the simulation data and test data. Comparing with the theoretical values, the mean error of the identification results of two simulations are 0.360 % and 0.865 %. we can see that the identification accuracy is relatively high, and the model can be used for parameters identification of the real system.

Fig. 3Pressure curves identified by mathematical model

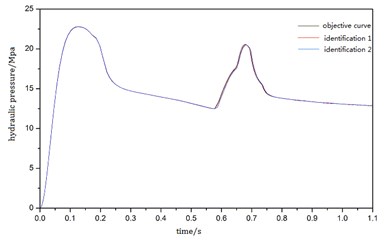
Fig. 4Pressure curves identified by test data

4.1. Description of the identification problem

The mathematical model used for identification is still the mathematical model of the manual recoil process of the cannon established above. In this section, the two parameters to be optimized are respectively the mainstream hydraulic resistance coefficient of recoil brake $k_1$ and the tributary hydraulic resistance coefficient of recoil brake $k_2$. The basic idea of interval analysis theory is to represent the real value by an interval including real value, and then to narrow the range of the interval by a series of interval operations. For the third type of parameters $k_1$ and $k_2$, a method combining PSO algorithm and interval analysis theory Krawczyk algorithm was proposed for identification. The identification process is as follows:

1) Giving the initial interval of uncertain parameters and sampling within the interval. Then the sampling values are substituted into the model to obtain the corresponding output, and the relative error between it and the target value is calculated.

2) Selecting the corresponding sampling value with the minimum relative error in the first step and taking it as the midpoint of the new interval. The middle point is subtracted from the upper and lower bounds of the original interval, and the result with small absolute value is taken as the radius of the new interval to generate the new interval of uncertain parameters.

3) If the midpoint calculated in the second step happens to be the midpoint of the original interval, reducing the original interval by 10 % and returning to the first step.

4) Repeat steps 1-3 until the relative errors of all the output values meet the accuracy requirement.

On the basis of identification in the above section, after determining the values of $P_{f0}$ and $n$, identifying the uncertain parameters $k_1$ and $k_2$ according to the above steps. The initial value of $k_1$ and $k_2$ are set to [1.2, 1.76] and [1.8, 2.64]. After setting the value of each parameter in the model, the iterative calculation can be conducted according to the Krawczyk algorithm process. After each iteration, choose new sample within the new range generated. The simulation is carried out according to the sample values and calculating the similarity degree of chamber P3 pressure between simulated data and target data. Finally, the iterative process is terminated according to whether the similarity meets the requirements.

4.2. Parameters identification results

Table 3 and Table 4 give the identification results of the simulation data and test data. The results of identification are evaluated by the uncertainty level of interval $\gamma \left(A^I\right)=A^w/\left|A^c\right|$ and relative error.