Nonlinear dynamic analysis for high speed gear-rotor-bearing system of the large scale wind turbine

1. Introduction

Gears system is considered to be one of the most important power transmission systems and has a widely applications such as wind turbine, automobiles, aircrafts, marine vehicles and other industries. Along with improvement of the gear rotational speed and increasing of transmission power, the gear vibration and noise have great influence, which not only is caused the deteriorative working environment, but also is caused by the nonlinearity such as the gear backlash, the variation in tooth mesh stiffness, the different support types and looseness. The mesh impact is also presented when the gear drive is under the conditions of the time-variable excitation. These nonlinear factors have a detrimental effect on dynamics of gear system.

It is well known that the gear mesh coupled influence and transmission error excitations cause the dynamic behaviors of gear rotor bearing system different from the general rotor system. Under the effects of internal and external excitations, the dynamic characteristics of the gear rotor bearing system might become more complicated, and some new vibrational features might be found. In order to understand dynamic characteristics of gear drives and enhanced load carrying capacity and reliability, it is very important to establish exact dynamic model and to analyze coupled lateral-torsional vibration of a geared rotor system. In recent years, a great number of theoretical researches have been carried out in order to reveal the dynamic characteristics of the vibration system due to interaction effects of internal excitation and external excitation. Wang [1] detailedly reviewed the mathematical models and the solving methods for the non-linear dynamics of geared systems and discussed the critical issues for further research on the nonlinear vibration in gear system.

In earlier studies, a great number of torsional dynamic models have been proposed in order to reveal the dynamic characteristics of the gear system. Kahraman [2] analyzed non-linear frequency response characteristics of a spur gear pair considering backlash for both external and internal excitations with harmonic balance method (IHBM). Huang [3] presented a time-varying model to investigate dynamic responses of spur gear and time-varying damping was directly used to account for the lubrication film of tooth pairs. The lubricant damping factor and its effects on gear dynamics was also discussed, and the effects of the lubricant viscosity and applied torque on the gear dynamics were thoroughly investigated. Wang [4] presented a generalized nonlinear time-varying dynamic model of a hypoid gear pair with backlash nonlinearity. The effects of mean load and mesh damping were analyzed and jump discontinuities, sub-harmonic and chaotic behaviors were obtained. Velex [5] established a relation between dynamic tooth loads and quasi-static transmission errors of helical gear sets based on both single and multi-degree of freedom models. Cheon [6] used four different analysis models to identify the effects of hydrodynamic force and friction force on the dynamic behaviors of gear. The results indicated that the viscosity had a strong effect on the behavior of gear pair systems, friction had very little effect on torsional behavior. Osman [7] studied a specific 3D dynamic gear model, which is combined to contact fatigue model accounting for crack initiation and propagation. The numerical findings compare well with the experimental evidence from a back-to-back test rig. Ma [8] analyzed the nonlinear dynamic and vibration characteristics of spur gear pair with local spalling defect to investigate the effect of spalling defect on mesh stiffness and dynamic response and obtained four different stages analytical solutions with the time-variant stiffness in a mesh period. Rincon [9] described an advanced model for the analysis of contact forces and deformations of spur gear by using a finite element model and an analytical approach. And discussed the quasi-static behaviour of a single stage spur gear system. Hu [10] studied the effect of mesh stiffness on the dynamic response of 6-DOF face gear transmission system combining with backlash nonlinearity. The effect of mesh stiffness on the dynamic characteristics of the face gear drive system was analyzed with two patterns as time-varying form and time-invariant form. Chen [11] used the introduction of fractal theory to evaluate the gear backlash, and combined with the tradition gear torsional model, and the effect of gear dynamics were studied by changing backlash based on fractal theory. Farshidianfar [12] studied the global homoclinic bifurcation and transition to chaotic behavior of a nonlinear spur gear pair by means of Melnikov analytical analysis, and predicted the threshold values of the control parameter for the occurrence of homoclinic bifurcation and onset of chaos. Zhou [13] analyzed the nonlinear characteristics of gear transmission system under the action of external and internal excitations by the IHBM, and the vibration response obtained by IHBM compared very well with the results obtained by Newmark method. Wei [14] investigated the dynamic responses of a torsional vibration geared system with uncertain parameters by using the Chebyshev interval method. The effects of those uncertain parameters on the frequency response of the dynamic mesh force were discussed in detail, and the results show that parameter uncertainties might be propagated in the vibration system and leaded to relatively large uncertainties of the dynamic response of system. Zhu [15] used the HBM to investigate the nonlinear dynamics of a purely rotational nonlinear dynamic model of a typical Ravigneaux compound planetary gear sets. The nonlinear dynamic characteristics of the gear sets were researched, and the effect of nonlinearities on the frequency response characteristic were investigated by changing parameters. Yoon [16] established a simplified purely torsional concentrated parameter model of wind turbine gearbox and investigated the vibro-impact energy of unloaded gears using the HBM.

In order to preferably investigate the nonlinearity of the spur gear rotor bearing system, many researchers develop coupled lateral-torsional models and perform a lot of experiment works. Choi [17] studied the coupled lateral-torsional vibration of a geared rotor-bearing system by the transfer matrix method. The natural frequencies and corresponding mode shapes, and whirl frequencies under different spin speeds were analyzed. Lee [18] examined the coupled vibration characteristics of a turbo-chiller rotor bearing system having a bull-pinion speed increasing gear, using a coupled lateral and torsional vibration finite element model of a gear pair, and compared the uncoupled and coupled natural frequencies and their mode shapes with varying gear mesh stiffness. Chaari [19] proposed to quantify the reduction of gear mesh stiffness with two common tooth faults: spalling and breakage taking into account bending, fillet-foundation and contact deflection and the vibration signatures of each tooth fault was identified. Kim [20] analyzed the dynamic response of a pair of spur gears due to bearing deformation, which regarded the pressure angle and the contact ratio as time-varying variables. Zhou [21] developed a modified mathematical model for simulating gear crack from root with linear growth path in a pinion. And a 16-DOF dynamic model of a one-stage spur gear system was used to study the response of the system considering time-varying meshing stiffnesses and different levels of crack growing in the pinion. Chen [22] established a dynamic lumped-parameter gear model, which was employed to examine the effects of engine torque fluctuations and tooth surface friction on the gear rattle response and the corresponding tooth impact behavior. Wang [23] investigated the effects of random perturbation of a low-frequency excitation caused by torque fluctuations, gear damping ratio, gear backlash, meshing frequency and meshing stiffness, which had different effects. Jiang [24] proposed a 6-DOF analytical helical gear model by incorporating the time-varying sliding friction and mesh stiffness based on the changes of friction force and mesh stiffness. The results show that the oscillations of the dynamic responses became more significant at both the beginning and the end of the spalling area, especially with the growth of the spalling size. Cui [25] established nonlinear dynamic model of gear-flexible shaft-bearing system considering backlash, time-varying mesh stiffness and radial clearance of bearing, and studied the effects of backlash, crack in shaft and tooth wear faults. Mohmmed [26] modelled a one-stage reduction gear using three different dynamic models (with 6, 8 and 8 reduced to 6 DOF), as well as the developed model (with 12 DOF). The dynamic simulation was performed for different crack sizes, and time domain scalar indicators were applied for fault detection analysis. Ma [27] investigated the dynamic behaviors of a perforated gear system considering effects of the gear crack propagation paths and focused on the effects of a crack propagating through the rim on the time-varying mesh stiffness and vibration responses.

Eccentricity, which is caused by installation and manufacturing in the design of gears is one of the sources inducing the nonlinear dynamic behaviors. Based on the finite element approach, Lee [28] analyzed the unbalance response orbit of a gear-coupled two-shaft rotor-bearing system, and bumps were observed at the first torsional natural frequency because of the coupling between the lateral and torsional dynamics due to gear meshing. Zhou [29] proposed the wind turbine gearbox system, which was divided into three-class gear transmission, and the dynamical models of spur gear, helical gear and planetary gear were established. But it did not dynamics simulation. Dou [30] established a coupled flexural and torsional model of a spur geared rotor system and studied the influence of gear geometric eccentricity on the dynamic responses of the system. Cui [31] presented a dynamic model of the geared rotor oil journal bearing system considering the nonlinear gear mesh force, nonlinear oil film force and eccentricity, and investigated the effect of oil film force on system. Wan [32] presented a series of investigations into the dynamic behavior of a gear-bearing system with nonlinear suspension, nonlinear oil-film force, nonlinear gear mesh force and eccentricity. The results provided an understanding of the operating conditions under which undesirable dynamic motion took place in a gear-bearing system. Zhang [33] presented a general 3-D dynamic model of a multi-shaft helical geared rotor system with geometric eccentricity and the transmission error, and analyzed geometric eccentricity and the coupling between gear geometric eccentricity and rotor mass unbalance. Han [34] analyzed the dynamic behaviors of a geared rotor system under time-periodic base motions, and utilized the numerical method to obtain the lateral and torsional responses of the system under transmission error, unbalanced mass excitations and tooth root cracks. Compared with the pitching and yawing motions, the rolling base motion had the greatest impact on the dynamic behaviors of the geared system. Gao [35] studied the nonlinear vibration characteristics of geared rotor bearing system with the interactions among gears, shafts eccentricity, and plain journal bearings. The nonlinear oil-film forces were computed with the Reynolds equation for finite-length journal bearings, and the responses of meshing vibration and bearing vibration were discussed.

It should be noted that in all the above researches, the nonlinear dynamic behaviors of the gear system are analyzed under internal or external excitation respectively. It is noteworthy that the dynamic excitations in gear systems are composed of internal and external excitations. Eccentricity, which is caused by installation and manufacturing in the design of gears is one of the sources which induces the strong nonlinear dynamic behaviors. In addition, gravity is a fundamental vibration source in spur gear system and plays an important role in the system dynamic response compared to excitations from tooth meshing alone. The nonlinear dynamic characteristics of the system with backlash, eccentricity, gravity, time-variant meshing stiffness and transmission errors have been scarcely studied. In this paper, an 8-DOF, coupled lateral-torsional vibration dynamic model of high-speed gear rotor bearing system is proposed, which belongs to a part of a wind gearbox. In addition, the fluctuation characteristic of input/output torque should be considered in this model due to the random fluctuation of the wind load and electromagnetic excitation. The effects of error fluctuation and load fluctuation on the dynamic characteristics are analyzed, providing a fundamental understanding of the dynamic features of coupled lateral-torsional vibration of gear rotor bearing system.

The rest of this paper is organized as follows: after this introduction, in Section 2, the nonlinear dynamic model of an 8-DOF coupled lateral-torsional vibration dynamic model is established with backlash, eccentricity and time varying stiffness. In addition, the transmission error is also considered in the system as a parametric excitation. The influences of the key parameters are studied with 3-D frequency spectrum, bifurcation map, respectively. In the last section, some conclusions are presented.

2. Dynamic model of the spur gear rotor bearing system

2.1. The lumped mass model of the gear system

An 8-DOF lumped parameter dynamic model taking into account the coupled lateral-torsional vibration is developed to investigate the coupled multi-body dynamics of the spur gear-rotor-bearing system in Fig. 1. The gears are modeled as rigid bodies attached to torsionally flexible shaft that is supported by rolling bearing represented by a set of discrete stiffnesses and dampings, respectively. Fig. 1(a) presents a schematic illustration of the dynamic model considered between driving gear and driven gear. Fig. 1(b) shows a simple mechanical model, retaining the essential characteristics which arise from the interaction of spur gear mesh and the bearing nonlinearities.

In Fig. 1, the bearings, gears and input/output are simulated by four lumped mass points and the corresponding points are connected by stiffnesses and dampings. In addition, the movements of the input/output in lateral direction are negligible and the torsional direction is considered (${\theta }_d$ and ${\theta }_l$). Each gear rotor has three DOFS including two lateral DOFS (${\theta }_{xi}$ and ${\theta }_{yi}$ ($i=$1, 2)) and one torsional DOF (${\theta }_1$ ($i=$1, 2)).

According to the principle of the gear mesh, the torsional angular displacements of gears, input/output are defined as follow:

1

${\phi }_d={\omega }_{1}t+{\theta }_d,\mathrm{}\mathrm{}\mathrm{}{\phi }_1={\omega }_{1}t+{\theta }_1,\mathrm{}{\phi }_2={\omega }_{2}t+{\theta }_2,\mathrm{}\mathrm{}\mathrm{}{\phi }_l={\omega }_{2}t+{\theta }_l,$

where, ${\omega }_1$ and ${\omega }_2$ represent the angular velocities of driving and driven gears

Taking the eccentricity into account, the relationship of the center of rotational $O_i$ ($x_i$, $y_i$) and center of mass $G_i$ ($x_{gi}$, $y_{gi}$) ($i=$1, 2) can be expressed:

2

$x_{g1}=x_1+{\rho }_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1,\mathrm{}\mathrm{}\mathrm{}{y}_{g1}=y_1+{\rho }_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1,x_{g2}=x_2+{\rho }_2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2,\mathrm{}\mathrm{}\mathrm{}{y}_{g2}=y_2+{\rho }_2\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2.$

Fig. 1Dynamic model of spur gear rotor bearing system

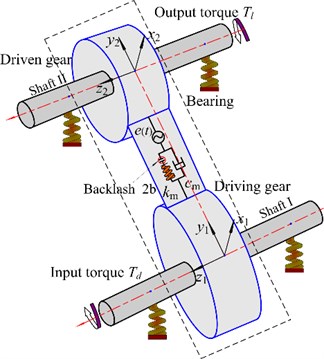
a) Schematic illustration of system

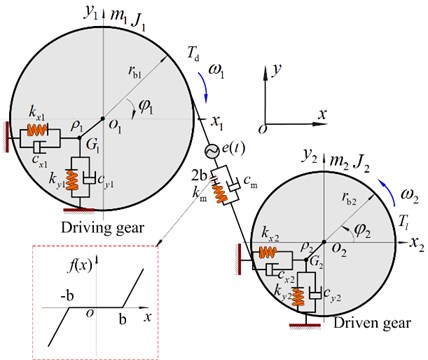
b) Dynamic model of system

With the consideration of backlash nonlinearity, the dynamic mesh force $F_m$ between driving gear and driven gear can be written as:

3

$F_m=\left\{\begin{array}{ll}{c}_m\dot{\delta }+k\left(t\right)\left(\delta -b\right),& \delta >b,\\ 0,& -b<\delta <b,\\ c_m\dot{\delta }+k\left(t\right)\left(\delta +b\right),& \delta <-b,\end{array}\right.$

where, $c_m$ is the mesh damping, $b$ is the half of the gear backlash, $k\left(t\right)$ represents the time-variant mesh stiffness and.

Fig. 2Time-varying mesh stiffness

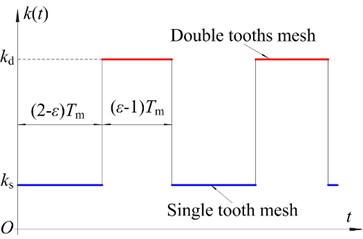
Time-varying mesh stiffness is an important high frequency harmonic excitation in gear system, which is caused by the alternation of single and double teeth mesh. As shown in Fig. 2, it contained two parts: the minimum value of stiffness ($k_s$) is in the one pair of tooth contact zone and the maximum value of stiffness ($k_d$) is corresponding to two pairs of tooth contact zone. In addition, the time varying gear mesh stiffness is a periodic excitation with the contact ratio $\epsilon$ ($\epsilon <$ 2) and a mesh period $T_m$ ($T_m=2\pi /z_1{\omega }_1=2\pi /z_2{\omega }_2$).

Considering the coupled lateral-torsional vibration of gear rotor bearing system, the dynamic transmission error $\delta \left(t\right)$ along the line of action can be written:

4

$\delta \left(t\right)=\left(r_{b1}{\phi }_1-r_{b2}{\phi }_2\right)+\left(x_{g1}-x_{g2}\right)\mathrm{s}\mathrm{i}\mathrm{n}\alpha +\left(y_{g1}-y_{g2}\right)\mathrm{c}\mathrm{o}\mathrm{s}\alpha -e\left(t\right),$

here, $r_{b1}$ and $r_{b2}$ are the base radii of driving gear and driven gear, $\alpha$ is the pressure angle of the gears. And $e\left(t\right)$ is the static transmission error:

5

$e\left(t\right)=e_m+e_r\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_m+{\phi }_m\right),$

in which, $e_m$ represents the mean and $e_r$ indicates the fluctuation of transmission, respectively. ${\phi }_m$ represents the initial phase angle.

3. Analysis of the dynamic responses

In this section, the model parameters about the spur gear rotor bearing system are listen in Table 1, and the dynamical simulation of gear drives, considering different kinds of work conditions and influence factors, will be analyzed. In order to understand the vibration characteristics of the gear rotor bearing system intuitively, the detailed simulation condition schematic is shown in Fig. 3.

Fig. 3Simulation condition schematic

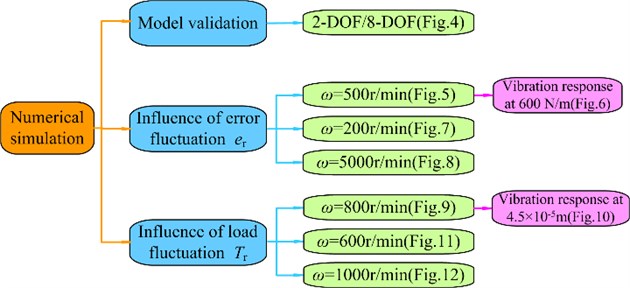
3.1. Model validation

In order to verify the accuracy of mathematical model with 8-DOF gear system, the time response obtained from the proposed equations is compared to the time response from the equations of Shen [36]. The Eq. (8) presents by Shen [36] the mathematical model of 2-DOF gear system, which can be expressed as follow:

8

$J_a\frac{d^2{\theta }_a}{d{t}^2}+c\left(R_a\frac{d{\theta }_a}{dt}-R_b\frac{d{\theta }_b}{dt}-\frac{de}{dt}\right)\cdot R_a+R_{a}K\left(t\right)f\left(R_a{\theta }_a-R_b{\theta }_b-e\left(t\right)\right)=T_a,$
$J_b\frac{d^2{\theta }_b}{d{t}^2}-c\left(R_a\frac{d{\theta }_a}{dt}-R_b\frac{d{\theta }_b}{dt}-\frac{de}{dt}\right)\cdot R_b-R_{b}K\left(t\right)f\left(R_a{\theta }_a-R_b{\theta }_b-e\left(t\right)\right)=-T_b.$

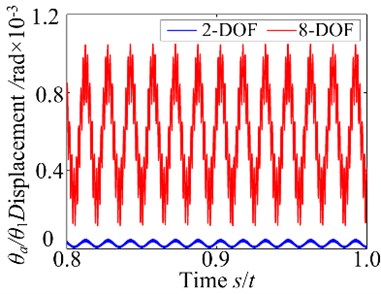
In this section, the models (2-DOF and 8-DOF) are simulated by the same parameters. The torsional vibration waveforms of 2-DOF (blue line) and 8-DOF (red line) are shown in Fig. 4.

It can be seen that there is obvious difference between the vibration responses obtained by two different spur gear models. Comparing the results of Shen [36] with the results of the presenting study, the vibration amplitudes of the presenting study are relatively larger than those of Shen [36], which shows some differences in the magnitudes of vibration. The reason is that the presenting study includes the effects on eccentricity, gravity, elastic deformation of shaft, the fluctuation of input/output torque and coupled lateral-torsional vibration, which is not considered in Shen [36]. It is also observed from Fig. 4 that the harmonic component has significantly changed due to the influence of bearing. Therefore, the spur gear model in this study is more realistic than the model of Shen [36].

For better analysis the dynamic characteristics of gear rotor bearing system, more numerical computations are carried out and the dynamic responses of gear system are obtained. Due to the effects of external environment and gear mesh, the loads and transmission error have the time-variant characteristic, which represent the internal and external excitations. Therefore, in the following analysis, the influences of error fluctuation ($e_r$) and load fluctuation ($T_r$) will be analyzed of the spur gear rotor bearing system. Only vibration responses of the driving gear are shown by 3-D frequency spectrums, bifurcation diagrams, time-domain waveform, phase diagram and Poincaré map.

Fig. 4Vibration waveform (at ω= 4000 r/min)

3.2. Effect of the error fluctuation on dynamic response

Transmission error is one of a key parameters affecting the dynamic behaviors of the gear rotor bearing system, which is caused by installation and manufacture error. Because transmission error is contained in the relative displacement and the backlash is a piecewise function of relative displacement. In addition, the transmission error exists alternate characteristics, which affects the degree of nonlinearity of the gear rotor bearing system and the vibration response. In order to illustrate the influence on the error fluctuation $e_r$, the 3-D frequency spectrum and bifurcation diagram of the gear system $\omega =$800 r/min, are illustrated in Fig. 5. The 3-D frequency spectrum, as shown in Fig. 5(a), is presented in y direction. It can be observed that the rotational frequency $f_r$ and mesh frequency $f_m$ are the main frequency components, and complicated combination frequency and multiplication frequency components about 3$f_r$, $f_m-$2$f_r$, $f_m+$2$f_r$, $\text{2}{f}_m-f_r$, 2$f_m$, etc. appear. Besides, the amplitude of the $f_m$ is the second largest after that of the $f_r$ in the range of $e_r\in$[0, 0.7]×10^-5 m and the amplitudes of $f_r$ and $f_m$ increase markedly with the increasing error fluctuation. The quasi-periodic motion is correspondingly shown in the bifurcation diagram Fig. 5(b). With the increase of the error fluctuation, the amplitude of $f_m$ is the largest than those of other combination frequency components and the gear system transforms to $n$T-periodic motion from quasi-periodic motion. The amplitude $f_r$ increases obviously, and the amplitude of $f_m$ keeps constant in the range of $e_r\in$[0.7, 3.2]×10^-5 m. For the system with higher error fluctuation from 3.2×10^-5 m to 5.0×10^-5, the high frequency harmonic and continuous frequency components appear, and the amplitude of $f_m$ increases obviously. Combined with the related bifurcation diagram, the system shows chaotic motion. The $n$T-periodic motion, quasi-periodic motion and chaotic behavior appear in the spur gear rotor bearing system from a light error fluctuation to high error fluctuation condition. According to the analysis of the 3-D frequency spectrum and bifurcation diagram of the gear system, a path to chaotic motion though periodic and quasi-periodic is observed.

Above all, the gear system presents complex dynamic characteristics and strong nonlinearity. In order to analyze the dynamic behaviors more deeply, Fig. 6 shows the vibration responses at $e_r=$4.8×10^-5 m. It can be observed that the system exists non-periodic motion in Fig. 6(a). The continuous frequency components present in Fig. 6(b), and the phase diagram is highly disordered. Furthermore, the chaotic motion can be proved through irregular points in Poincaré map in Fig. 6(d).

Fig. 53-D frequency spectrum and bifurcation diagram of the gear system at 800 r/min

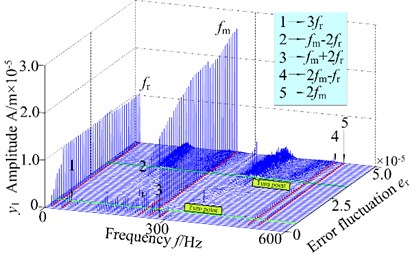
a) 3-D frequency spectrum

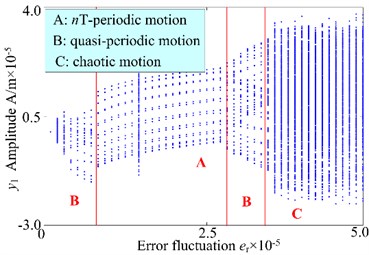
b) Bifurcation diagram

Fig. 6Vibration response of the gear system at 800 r/min

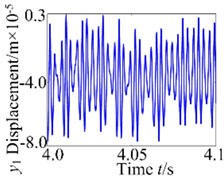
a) Vibration waveform

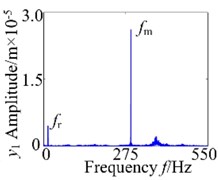
b) Frequency

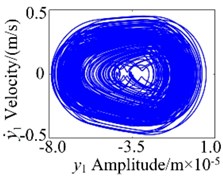
c) Phase diagram

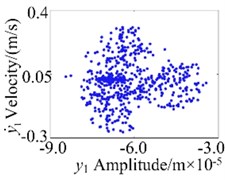
d) Poincaré map

In order to analyze more deeply, the dynamic response of the system under $\omega =$600 r/min and 1000 r/min are investigated and the dynamic responses are shown in Fig. 7 and Fig. 8. The gear system presents strong nonlinearity with the periodic motion, quasi-periodic motion, chaotic behavior and jump phenomenon. According to the comparison of 3-D frequency spectrum and bifurcation diagram of the gear system with the different rotational speed, it can be seen from Fig. 5, Fig. 7 and Fig. 8 that the $f_r$ and $f_m$ are the demined responses under different rotational speed. The amplitude of $f_m$ exists jump phenomena turns backward ($e_r=$0.7×10^-5 m at $\omega =$800 r/min $e_r=$1.1×10^-5 m at $\omega =$800 r/min) and the chaotic region of the gear system narrows down ($e_r\in$[3.2, 5.0]×10^-5 m at $\omega =$800 r/min $e_r\in$[3.5, 5.0]×10^-5 m at $\omega =$800 r/min) with the increasing of the rotational speed. Furthermore, the amplitudes of the frequency components increase slightly. The above analysis shows that the error fluctuation has an important of the dynamic characteristics of the spur gear rotor bearing system. The increase of the error fluctuation increase the vibration amplitude and narrows the region of the chaotic motion.

3.3. Effect of the load fluctuation on dynamic response

Based on the above analysis, it is clear that the load fluctuation $T_r$ is an important parameter affecting the stability of the spur gear rotor bearing system. In this section, keeping other parameters remain the same, and the corresponding 3-D frequency spectrum and bifurcation diagram and of the system with $\omega$ as control parameter in the range of $T_r\in$[0, 900] N/m are illustrated in Fig. 9. It can be seen from Fig. 9(a) that the rotational frequency $f_r$ and mesh frequency $f_m$ components are obvious and the amplitude of $f_m$ is largest than others in the range of $T_r\in$[0, 120] N/m, which indicates the internal excitation is dominated excitation in the system, because the external excitation relatively lesser. In addition, the quasi-periodic motion is correspondingly shown in the bifurcation diagram for every load fluctuation in Fig. 9(b). However, as $T_r$ increases from 120 N/m to 560 N/m, the amplitude of $f_r$ increases markedly compared with those of other frequency components. The amplitude of $f_m$ nearly keeps constant with increasing load fluctuation in the range of $T_r\in$[120, 160] N/m and the $f_m$ increases slightly at $T_r\in$[160, 560] N/m. However, the amplitude of $f_r$ exceeds $f_m$ at $T_r=$ 325 N/m. It can be observed that the external excitation has larger influence than internal excitation. In addition, the frequency components of the gear system in different load fluctuation appears complicated frequency and continuous frequency components. In bifurcation diagram, it is clear that the gear system presents chaotic motion, which shows that the gear system motion becomes more complicated and unstable with the increasing load fluctuation. At higher values of the load fluctuation, i.e. $T_r\ge$560 N/m, the frequency components in the 3-D frequency spectrum in different ranges of load fluctuation include complicated multiplication frequency about 11$f_r$, 13$f_r$, 14$f_r$, 15$f_r$, 16$f_r$… and combination frequency components such as $f_m-$3$f_r$, $f_m-f_r$, $f_m+f_r$, $f_m+$2$f_r$, $f_m+$3$f_r$, etc. And the rotational frequency $f_r$ is much higher than those of synchronous vibrations. Furthermore, Fig. 1(b), the system motion is from $n$T-periodic motion in the range of $T_r\in$ [560, 610] N/m, through quasi-periodic motion at 610 N/m $<T_r<$670 N/m, to $n$T-periodic motion in the range of $T_r\in$[670, 780] N/m. Finally, the system exhibits quasi-periodic motion through periodic motion.

Fig. 73-D frequency spectrum and bifurcation diagram of the gear system at 600 r/min

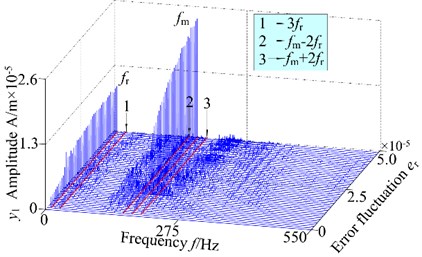
a) 3-D frequency spectrum

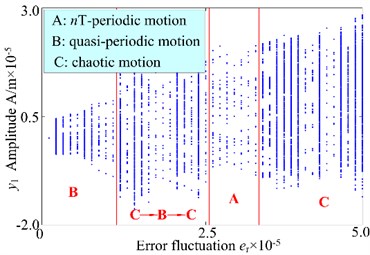
b) Bifurcation diagram

Fig. 83-D frequency spectrum and bifurcation diagram of the gear system at 1000 r/min

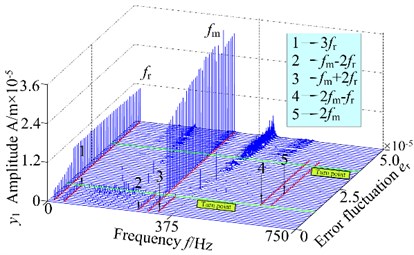
a) 3-D frequency spectrum

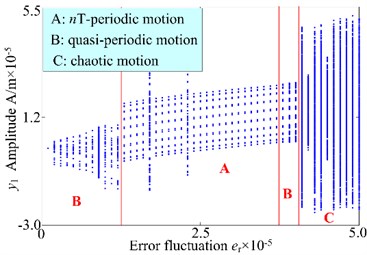
b) Bifurcation diagram

The vibration responses of the gear rotor bearing system at $T_r=$600 N/s are shown in Fig. 10. From the figures, it indicated that the system motion is $n$T-periodic motion, and the amplitude of $f_m$ is the second largest after that of the $f_r$, in addition, combination frequency and multiplication frequency components about $f_r$ and $f_m$ can also be observed, as is shown in Fig. 10(b). The phase diagram of the system in $y$ direction shows regular motion in Fig. 10(c). The system $n$T-periodic motion can also be verified by several discrete points in the projection of Poincaré map, as shown in Fig. 10(d).

Fig. 93-D frequency spectrum and bifurcation diagram of the gear system at 500 r/min

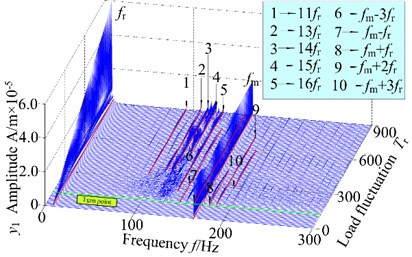
a) 3-D frequency spectrum

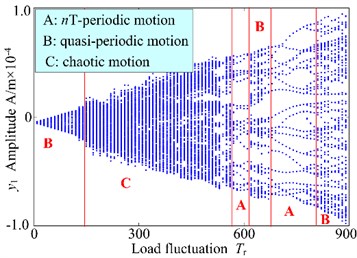
b) Bifurcation diagram

Fig. 10Vibration response of the gear system at 600 N/s

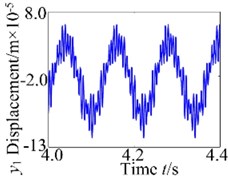
a) Vibration waveform

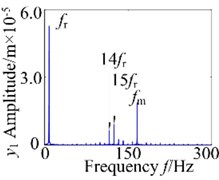
b) Frequency

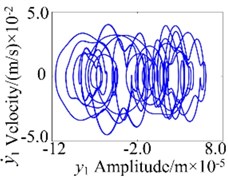
c) Phase diagram

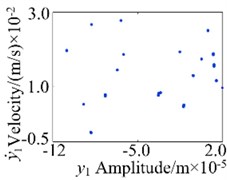
d) Poincaré map

Due to the load fluctuation, it is an important parameter affecting the dynamic behaviors of the spur gear rotor bearing system. In this section, the vibration responses of the gear system will be investigated at two constant rotational speed of 200 r/min and 1500 r/min, and 3-D frequency spectrums and bifurcation diagrams are illustrated in Fig. 11 and Fig. 12, respectively. Comparing Fig. 9, Fig. 11 and Fig. 12, the responses of the gear system exhibit some different dynamic phenomena. The 3-D frequency spectrums indicate that the rotational frequency and mesh frequency are the dominated responses. In addition, the amplitude of $f_r$ increase obviously and the amplitude $f_m$ increases slightly with increasing load fluctuation under internal and external excitations. Furthermore, complicated frequency components appear with different rotational speed. When the rotational speed of the system is $\omega =$200 r/min, the multiplication frequency of $f_m$ with other combination frequency components exist, while, the multiplication frequency of $f_m$ vanishes when the rotational speed increases to 500 r/min. With the increase of rotational speed, the continuous frequency components lag and corresponding the chaotic motion also demonstrates the same phenomenon. In addition, the region of the chaotic motion relative to the whole range of load fluctuation broadens, and the extent of the chaotic motion also strengthen.

Take into consideration the 3-D frequency spectrum and bifurcation diagram of the dynamic system, the influences of load fluctuation on the dynamic behaviors are obvious. For the system with the low rotational speed, the chaos behavior turns out more easily, and the vibration intensity relatively weak. With the increase rotational speed, the vibration amplitude obvious increase, and the characteristics of the chaos strengthen.

Fig. 113-D frequency spectrum and bifurcation diagram of the gear system at 200 r/min

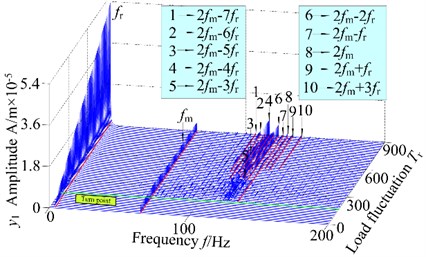
a) 3-D frequency spectrum

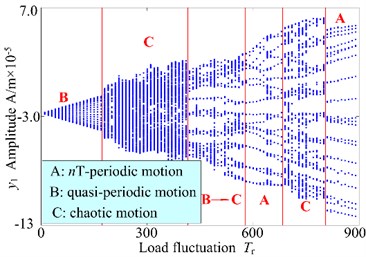
b) Bifurcation diagram

Fig. 123-D frequency spectrum and bifurcation diagram of the gear system at 1500 r/min

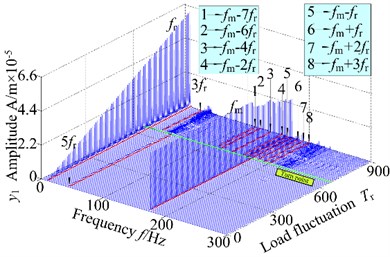
a) 3-D frequency spectrum

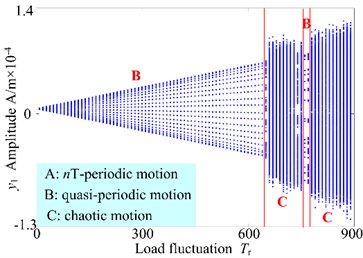
b) Bifurcation diagram

4. Conclusions

In this paper, an 8-DOF model of gear rotor bearing system is presented in which the dynamic behaviors of the structure is coupled with the vibration of the driving/driven gear. The dynamic model considers backlash, transmission error, eccentricity, gravity and external excitation, which are the main sources of the vibration excitation. The effects of the different parameters have been studied and the conclusions can be summarized as follows:

1) The results presented in this study provided a detailed understanding of nonlinear dynamic response of the gear rotor bearing system under error fluctuation (internal excitation) and load fluctuation (external excitation) conditions, which enable suitable values of the key parameters to be specified such that chaotic behavior can be avoided and reducing the vibration amplitude of the gear system.

2) The error fluctuation has significant influence on the nonlinear dynamic characteristics of gear rotor bearing system. The system exhibits different motions such as periodic motion, quasi-periodic motion and chaotic motion under different error fluctuation conditions. At relatively low error fluctuation, the rotational frequency amplitude is dominated response, which indicates the external excitation is main excitation in the system. With the increase of the error fluctuation, the meshing frequency’s amplitude is larger than others and the error fluctuation obviously has effect on the system’s vibration, the internal excitation plays the leading role, which makes the system undergo chaotic behavior.

3) It can be seen that, with the increase of load fluctuation, the amplitude of $f_r$ increases obviously. The results indicate that the excitation force amplitude has an influence on the nonlinear dynamic characteristics and the increase of the excitation force amplitude makes the vibration amplitude increase but it may restrict the chaotic motion at some extent.

4) For the spur gear rotor bearing system, the dynamic behaviors are analyzed in light, middle and high rotational speed conditions. For error fluctuation, with the increase rotational speed, the vibration amplitude increase markedly and the region of the chaotic motion become narrow gradually. For loader fluctuation, at the low rotational speed, the chaos behavior turns out more easily, and the vibration intensity relatively weak. With the increase rotational speed, the vibration amplitude obvious increase, and the characteristics of the chaos strengthen and turns backward.