Ground-penetrating radar time-frequency analysis method based on synchrosqueezing wavelet transformation

2.1. SST algorithm

In practical engineering, one signal contains multiple components, and each of the components represents one feature. A signal is composed of a group of harmonics, and the remainder is expressed as follows:

where $A_i\left(t\right)$ is the amplitude and $r\left(t\right)$ is the residue.

The SST algorithm is based on wavelet analysis theory. In this study, $f\left(t\right)$ is processed with the following wavelet transform:

where $a$ is the scale factor, $b$ is the time shift, ${\phi }^{\mathrm{*}}\left(t\right)$ is the complex conjugate of the mother wavelet.

According to Plancherel theorem, $W_f\left(a,b\right)$ is the wavelet coefficient $f\left(t\right)$. The equation can be written as follows:

where $\widehat{\phi }\left(t\right)$ and $\widehat{f}\left(t\right)$ are the mother wavelet function $\phi \left(t\right)$ and signal $f\left(t\right)$, respectively, after Fourier transform is performed.

In ${\left(W_x\left(a,b\right)\right)}^{-1}{\partial }_b{W}_x\left(a,b\right)=i\omega$, the instantaneous frequency of $f\left(t\right)$ can be preliminarily estimated as follows:

In the synchrosqueezing phase, where $\left(a,b\right)\to \left({\omega }_x\left(a,b\right),b\right)$, the energy is converted from a time-scale plane to a time-frequency plane. The synchrosqueezing value of wavelet coefficients are obtained by determining the wavelet coefficients in the central frequency domain:

where $T_f\left(\omega ,b\right)$ is the wavelet synchrosqueezing coefficient.

When the signal is discrete, the wavelet synchrosqueezing coefficients are expressed as follows:

where ${\omega }_l$ is the central frequency in $[{\omega }_l-(∆\omega /2),{\omega }_l+(∆\omega /2\left)\right]$.

2.2. Comparative analysis of the continuous electromagnetic signal sample

We apply conventional wavelet transform, short-time Fourier transform, and SST algorithm to analyze the transient electromagnetic wave signal and to determine the solution of the SST algorithm for time-varying signal processing. The time-varying signal $f\left(t\right)$ of analytical expressions is represented as follows [18]:

Fig. 1a) Synthetic signal of time-varying electromagnetic signal, b) conventional wavelet transform, c) short-time Fourier transform, d) SST results

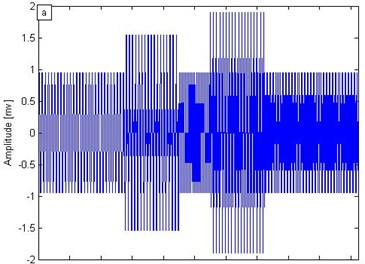
a)

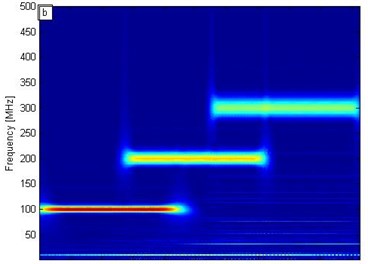
b)

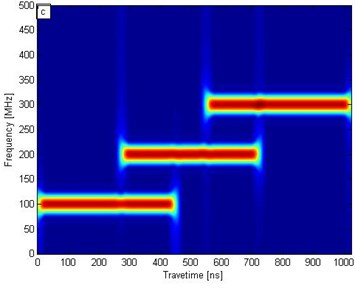
c)

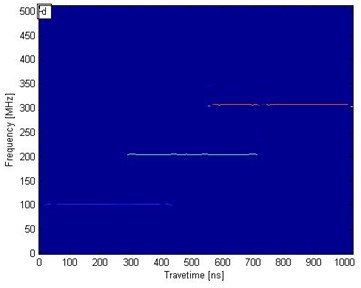
d)

The signal $f\left(t\right)$ mainly contains three main frequency components: 100, 200, and 300 MHz. The respective time sections are 0-499, 274-723, and 550-1024 ns. In the continuous signal $f\left(t\right)$ sampling, the sampling rate is 1000 and the time window is 1024 ns. Fig. 1(a) illustrates $f\left(t\right)$.

To analyze the effect of the SST algorithm on electromagnetic signal processing, we transformed $f\left(t\right)$ with SST, conventional wavelet transform, and short-time Fourier transform. Figs. 1(b), 1(c), and 1(d) correspond to the conventional wavelet transform, short-time Fourier transform, and SST frequency distribution contour, respectively. In Fig. 1(b), the wavelet transform results show that the frequencies of 100 and 300 MHz are detected at the highest and lowest resolutions, respectively; the resolution time-frequency decreases as the frequency increases. In Fig. 1(c), the short-time Fourier transform results demonstrate that frequency slightly influences resolution. In Fig. 1(d), the SST results reveal three straight lines corresponding exactly to three different frequencies: 100, 200, and 300 MHz. In Figs. 1(b), 1(c), and 1(d), the conventional wavelet transform and short-time Fourier transform results indicate an evident banded range, whereas the SST results accurately display the frequency and time location. Therefore, SST can distinguish time-frequency more precisely and yield a higher resolution than the two conventional conversion methods.

3.1. Forward numerical simulation model

GPR forward is its data interpretation basis. The finite-difference time-domain method (FDTD) is the most common numerical technique for solving the problems of the electromagnetic field. The FDTD method can be applied directly to the finite differential instead of Maxwell local field differential equations in order to get the field components of the finite difference formula. We use space grid to simulate purpose body having the same electrical parameters and set the appropriate initial and boundary conditions for field computing space to obtained the numerical solution of variables in Maxwell’s equations [19].

We use a three-layer structure model. The uppermost layer is air, the middle layer is concrete, and the bottom layer is dry sand. A rectangular void is placed in the dry sand layer. The model size and location are shown in Fig. 2. Both the concrete and sand layers have thicknesses of 0.15 m, while the internal hole size is 0.05×1.3 m. The GPR signal of the model can be obtained through numerical simulation.

Fig. 2Schematic of geometric model

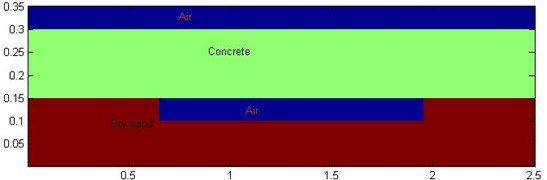
In the forward process, the parameters are dry sand permittivity Eq. (3), conductivity (0.0001 S/m), and concrete permittivity Eq. (6), conductivity (0.005 S/m). The set calculation area is 2.5 m×0.35 m, the computational grid size is 0.0025 m, and the time window is 12 ns. Ricker wave is employed as excitation, the dominant frequency is at 900 MHz, the transceiver antenna distance is 0.025 m, and the analogue sampling is 125 traces. The result was simulated by FDTD, as shown in Fig. 3. The FDTD method is performed for GPR signals of time series at all traces. Fig. 3 shows the GPR signal at first trace. The measurement line direction is the $x$-axis, and time is the $y$-axis in ordinate. The time-series signal of 125 traces is synthesized, and the result is displayed using image mode in Fig. 4.

Fig. 3GPR signal at first trace

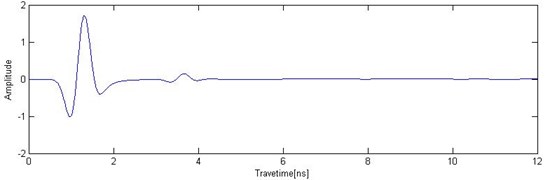
Fig. 4Forward numerical simulation signal of GPR

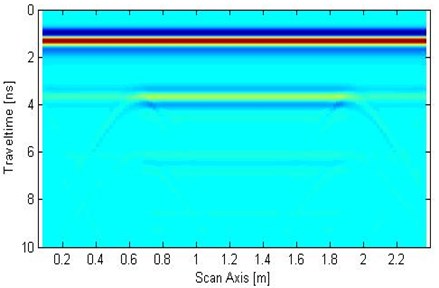
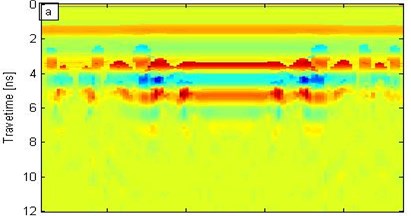
The wavelet modulus is obtained in the time-frequency domain and is synchrosqueezed for the wavelet synchrosqueezing modulus in the central frequency domain by utilizing the SST algorithm of the forward signal transform. Four frequency moduli, namely, 500 MHz, 900 MHz, 1.5 GHz, and 3.0 GHz are then analyzed (Fig. 5).

Fig. 5Different frequency wavelet synchrosqueezing moduli

a) 500 MHz

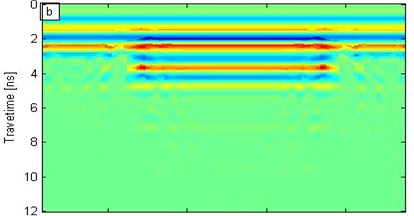
b) 900 MHz

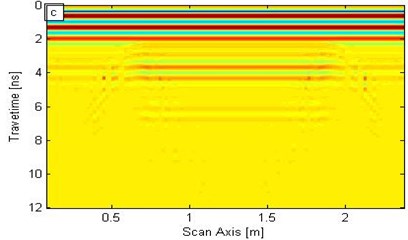
c) 1.5 GHz

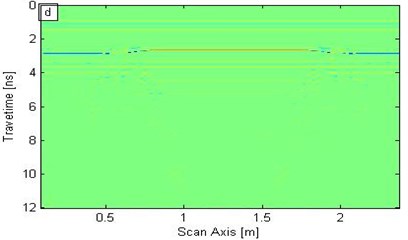
d) 3.0 GHz

In Fig. 5, the synchrosqueezing modulus exhibits low resolution when the frequency is relatively low; by contrast, the frequency is relatively high, the synchrosqueezing modulus yields high resolution, but the modulus strength is weak. Figs. 5(b) and 5(c) correspond to the frequencies of 900 MHz and 1.5 GHz, respectively; the void significantly affected the synchrosqueezing modulus. Figs. 5 (b) and 5(c) show that the modulus within a certain frequency range can identify the interface and defects. Therefore, the SST transformation can distinguish different interfaces and exceptions; furthermore, resolution increases as frequency increases. However, the modulus strength decreases as frequency increases.

3.2. Application analysis of tunnel lining detection

A tunnel lining detection signal is used as an example to evaluate the denoising effect of SST on practical engineering. The tunnel detection site is shown in Fig. 6(a). During the tunnel lining survey, there were three are three detection lines respectively located at the vault and the left and right waist. The three survey lines were arranged along the tunnel in the longitudinal direction. The three survey lines and the lining thickness for detecting defects, as well as the survey line layout are shown in Fig. 6(b).

Fig. 6GPR tunnel lining detection

a) GPR measurement on the spot

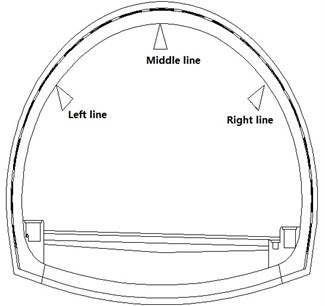
b) Measurement line sketch

The instrument employed in this analysis is LTD2100 GPR. The sampling center frequency is 0.4 GHz, the time window is 35 ns, and the trace spacing is 0.015 m. The chosen length of the target section is 8 m in left survey line. The detection results are shown in Fig. 7(a). The reflected signal of the secondary lining bottom interface appears within 10 ns of the simulation. The reflected signal is also a steel arch, which is shown in the initial lining. In general, the containing noise signal is denoising data minus original noiseless data, and the ratio of signal to noise energy is regarded as signal to noise ratio (SNR). We can use this parameter to measure the denoising effect. The formula is as follows:

where $S_{NR}$ is $SNR$, ${‖\cdot ‖}_2^2$ is square norm, $M$ is original noiseless data, and $S$ is containing noise data.

In the SST filtering process, referred to as SNR in this study, is 0.290 (−5.369 dB). The original signal in Fig. 7(a) joins the strong interference. White noise is added, and the result is shown in Fig. 7(b). With white noise interference, the interface between the second lining and the initial lining is extremely fuzzy, and the steel arch reflection signal in the primary lining is also not evident. The signal of the GPR is processed through SST filtering to verify whether the noise effect is removed [Fig. 7(b)].

In the SST filtering process, the signal is conducted through the SST conversion [Fig. 7(b)] is based on the SST theory in Section 2.1. A low-pass filter is used to separate more than 0.7 GHz signal. Then, the wavelet synchrosqueezing modulus is subjected to SST inverse transform [Fig. 8(b)]. In addition, the ‘db4’ wavelet is also adopted during conventional wavelet denoising for comparison to SST. Fig. 8(a) illustrates the result of the wavelet denoising function in MATLAB.

Fig. 7Detection section of GPR tunnel lining

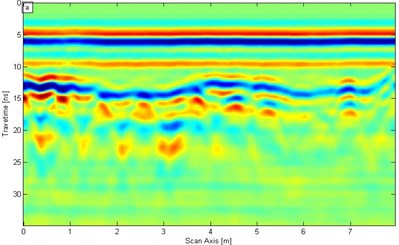
a) Original signal

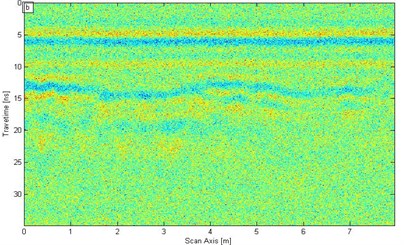
b) Addition of white noise signal

Fig. 8Signals after a) wavelet denoising and b) SST filter denoising

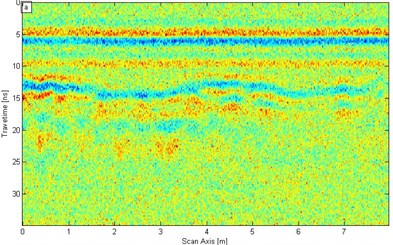
a)

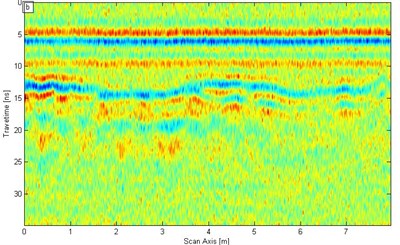
b)

We improve the signal resolution by using the two methods on the basis of the analysis of the results in Fig. 8. The lining structure, such as the interface between the second lining and the initial lining and the steel truss in the second lining are showed clearly in Fig. 8. However, the SST filtering effect is much clearer than conventional wavelet. After wavelet denoising is applied, according to Eq. (7) the SNR is 1.048 (0.203 dB); the SNR then increases 3.6138 times. After SST filter denoising is performed, the SNR is 3.261 (5.133 dB); the SNR then increases 11.2448 times. Therefore, the denoising effect of SST is much better than that of the conventional wavelet transform.