Abstract
The signal of electro-hydraulic servo system is non-stationary and time-varying due to the influence of vibration, noise and mechanical impact. The traditional digital filter always suffers delay in time domain and the delay increases along with the increasing of frequency. Considering the features of electro-hydraulic servo system, the Hilbert-Huang transform method is an effective method to decompose the original signal and obtain the noise components. Some improvements are made based on Hilbert Huang transform method and a new real time on-line filtering method is proposed in this paper. This improved filter is able to decompose out the noise components and other interference components from original signal, and remove them off in real time. Based on this new on-line filter, a new controller is also designed. Compared the filtering result with the traditional digital filter, this new controller’s control performance is much better.
1. Introduction
Due to the influence of the hydraulic transmission medium’s flow ability, compressibility, viscosity, and the influence of working environment such as temperature and pressure, the hydraulic cylinder sometimes works at some unusual states such as vibration, noise and impact [1]. The signal of electro-hydraulic servo system is non-stationary and time-variation. To filter these noise signals, the general solution is adding a digital filter into system. However, this solution also brings some problems such as phase delay and amplitude attenuation.
Hilbert-Huang transform (HHT) method [2] is proposed by Norden E. Huang et al. in 1998. This method is suitable for nonlinear and non-stationary signal analysis. At present, HHT technology has been used widely in the field of fault diagnosis, signal processing [3-5], oceanography [6] and so on [7, 8], and has obtained some good results. Considering the characters of electro-hydraulic servo system, HHT method can decompose out the noise components and other interference components from original signal, therefore, we are able to remove any unnecessary noise component. But the empirical mode decomposition (EMD) method which is a part of HHT method has some disadvantages when using in real time on-line filter, such as end point effect and computation efficiency. If we want to use the HHT method in electro hydraulic servo control system, some improvements on the EMD method are essential. Also, it is necessary to design a new controller based on this improved method.
2. Improvements of EMD method
2.1. Brief introduction of EMD process
EMD method can decompose out every single intrinsic mode function (IMF) from high frequency to low frequency, which is self-adaption. Most of these IMFs have their own physical meaning. The process of EMD method is described in the following steps 1-3.
Step 1: Find out all the local maximum and minimum points. The local maximum and minimum points of original signal is defined in Eq. (1) and Eq. (2):
Step 2: Select a kind of interpolation method and employ it between all extreme points, then get the envelope curve and .
Step 3: Calculate the difference according to Eq. (3). If does not satisfy Eq. (4), then repeat steps 1-3:
The first satisfied Eq. (4) is the first IMF, let , , be the original signal of next process round. Repeat steps 1-3, the rest of other IMF, , , …, will be decomposed out. When is a monotonic or constant series, this decomposition process will be terminated.
2.2. Optimizations of decomposition process
Review the whole process of EMD, the envelope curve is the key of decomposition. But the end point effect has significant influence on the decomposition [3], especially when the length of data is short. Many researchers have done a lot of work [9-12] to restrain the end point effect. To get a better filtering performance of short data, we make optimization of the EMD from four aspects as stated below.
Optimization 1: If the end point is the maximum or minimum point of the whole data section, then the end point will be treated as a local maximum or minimum point:
Optimization 2: The decomposition process may miss some turning points if the process follows the Eq. (1) and Eq. (2) strictly. And these missed turning points will reduce the effect of envelop curve as shown in Fig. 1. In this figure, and are two turning points, and they are not treated as local extreme points, so the envelop curves at point and are not complete: the max envelope curve is missed at point and the min envelop curve is missed at point . At next process round, the value of point will change to :
and the same thing will happen to point .
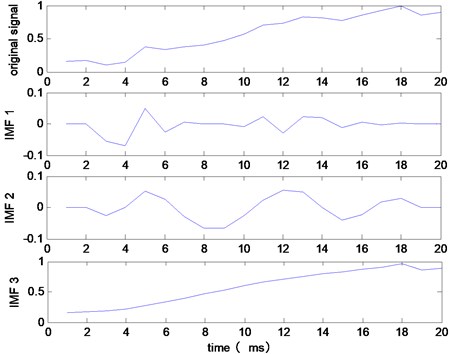
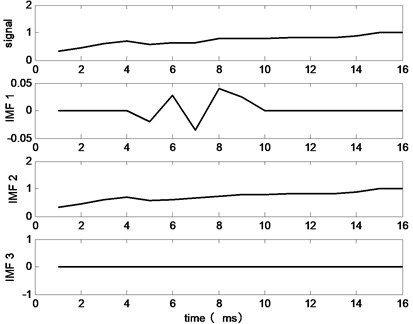
The decomposition result of Fig. 1 is shown in Fig. 2. We notice that the noise at point and is missed. Along with the further development of this decomposition process, and will also become 0. This effect will diffuse to the data center, then the data will be changed from to . This means that the filtering effect only works in the data’s center area. The decomposition result under this situation is shown in Fig. 3, from this figure it’s easy to see that all the noise components (IMF1-IMF3) are not ideal.
Therefore, the turning points should be included in the definition of local extremely points. The maximum point of turning point is redefined as Eqs. (5)-(6), and the minimum point of turning point is redefined as Eqs. (7)-(8);
Fig. 1Effect of turning point on envelope (a)
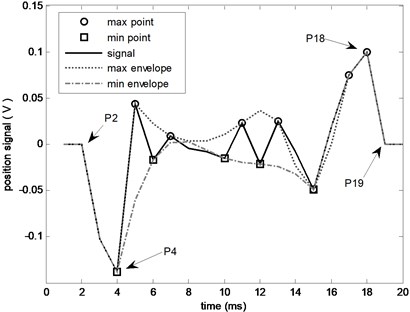
Fig. 2Effect of turning point on envelope (b)
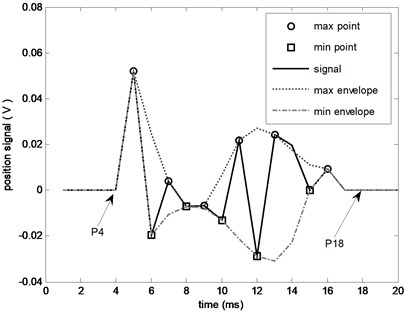
Fig. 3The decomposition result without considering turning points
After extending the definitions of local maximum and minimum points, the new max points, min points and envelope curves in Fig. 1 are shown in Fig. 4 and Fig. 5. The envelope curves can be obtained by using three spline interpolation method. With considering the point and , the max envelop curve and min envelope curve become complete. The value of point changes to : . At next process round, the decomposition result is shown is Fig. 5. In Figs. 4 and 5, we can notice that the diffusion effect of data changing into 0 no longer exists.
After using these revised definitions, the decomposition result of the signal in Fig. 3 is shown in Fig. 6. In this result, IMF1 and IMF2 are the noise components, IMF3 is the useful signal. Compared Fig. 6 with Fig. 3, the new filter works better, which means the optimization 2 is necessary and effective.
Optimization 3: The envelop curve may have overshoot or undershoot when the span between two local extreme points is too larger than others. This situation is shown in Fig. 7. As shown in this figure, the span between point and is , 53251. The other spans are to , , ,, the average value of these spans is , 23.75, . The undershoot (between point and ) of envelope curve will have a significant impact on the results. In this example, the value of local max points’ envelope curve is smaller than local min points’ envelope curve, which will introduce errors into final result. In this undershoot section, the envelope curve is ought to be the signal itself, the correct calculation process should be:
implying that there is no noise in the data of this section. But due to this undershoot, the calculation result becomes , indicating that the process will introduce some error noises into result.
Fig. 4The envelope effect with considering turning points (a)
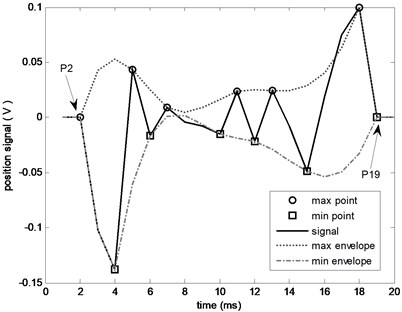
Fig. 5The envelope effect with considering turning points (b)
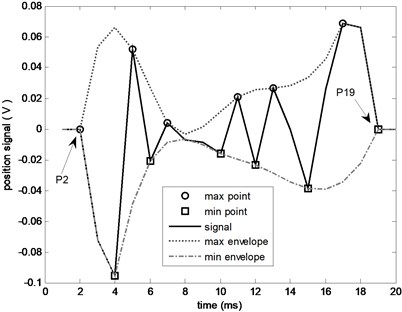
Fig. 6The decomposition result with considering turning points
In order to avoid this situation, interpolation method could be an outstanding solution. Firstly, the average span of can be calculated by Eq. (9), in which represents the span between two local extreme points and , . Secondly, find out the maximum span according to Eq. (10) and (11). Thirdly, insert points in the data section which has the maximum span. If the data is and local extreme points are , and the max span is between and , , so the exteme points will change to after interpolation, in which , :
in which is the length of data, is the number of span.
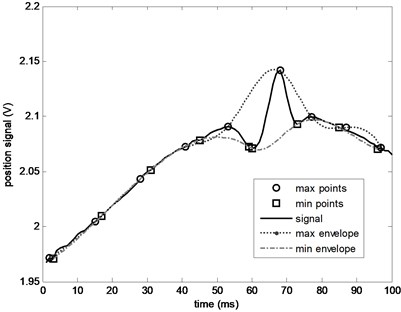
After applying this interpolation method, the envelop curve in Fig. 7 has been improved which is shown in Fig. 8.
Fig. 7The decomposition result after considering turning points
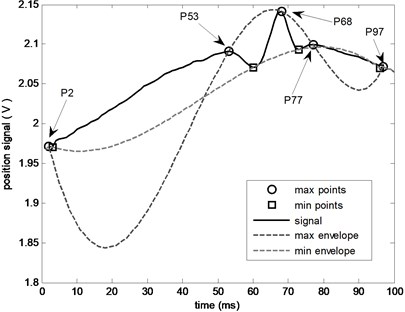
Fig. 8The envelop curve after interpolation
Optimization 4: In order to improve calculation efficiency and reduce operation time, a termination condition Eq. (12) is added. Because in some cases, the noise components are just in the first few IMFs, the filtering result will be inaccurate if the decomposition process runs to the final step ignoring Eq. (12). For example, if the noise components are , the other components are useful signals. The original signal is :
If the filter takes as noises, then the signal after filtering will be :
This situation is shown in Fig. 9, only is the noise component, is useful signal, and the filter takes the other IMFs as noise components, the filtering result will be all zeros.
To avoid this situation, Eq. (12) is employed to judge the similarity between the original signal and the decomposition component. If the decomposition result is similar to the original signal, the decomposition process should be stopped:
in which is the original signal, is the component.
Fig. 9The noise component is only in IMF1
3. The Design of on-line filter
The filtering process is carried out according to the following steps 1-8.
Step 1: Set the length of filtering window as n, when system acquires a new data point , update the data of this window from to .
Step 2: Find out all local maximum points according to the Eqs. (1), (5), (6), and all local minimum points according to the Eqs. (2), (7), (8). This step also follows the optimization 1.
Step 3: Following optimization 3, and become and .
Step 4: In the array of and , the three spine interpolation method is performed in range and , so the envelop of maximum points is :
In the same way, . The rest sections in range take the original data itself as the envelope curve, after this the and become and :
Step 5: Let , then . Determine whether the process needs to be terminated according to Eqs. (4) and (12). If not, repeat the steps 2-5 until Eqs. (4) and (12) are satisfied. After these steps, the rest of is one , i.e., .
Step 6: The original data minus is the original signal of next process round. For signal , repeat steps 2-5 then can be decomposed out. In the same way, the others , ,…, also can be decomposed out.
This whole decomposition process can be represented in Table 1.
3.1. The order of noise components
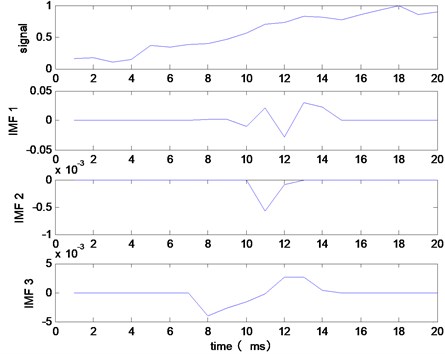
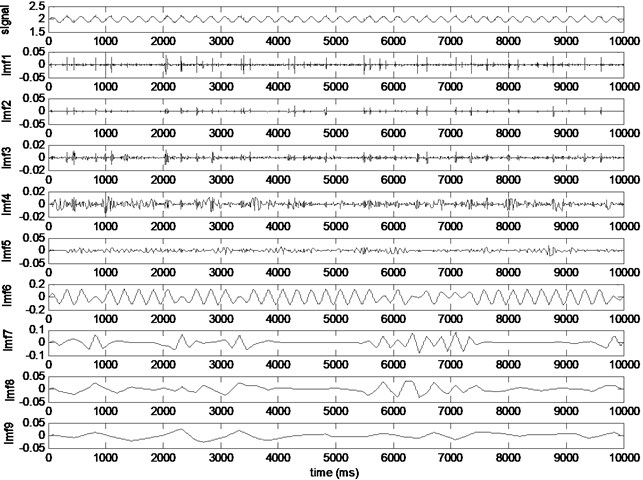
Before the start of decomposition process, the order of noise components needs to be determined. Decompose the acquired data of electro-hydraulic servo system by using EMD method, and the result is shown in Fig. 10. The noise components are mainly in the first few components -, therefore, the process should be ended at . The signal becomes after filtering, .
Table 1The whole process of filtering decomposition
Signal | |||||
0 | - | - | - | ||
1 | - | - | - | - | |
2 | - | - | - | - | |
3 | - | - | - | - | |
1 |
Fig. 10The decomposition result
3.2. The length of filtering window
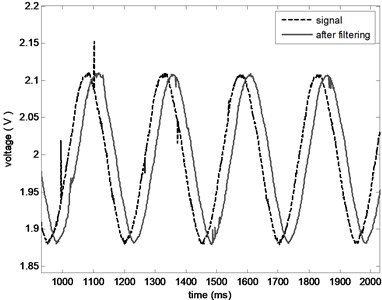
The length of filtering window is vital to filtering process. On one side, the longer the window is, the more information it contains. On the other side, the longer the window is, the more time and the bigger phase delay it takes. Therefore, a trade-off between these two sides is necessary. Compare the results of length 20 and length 50, which are shown in Fig. 11 and Fig. 12, respectively, the length of this system is determined to 50.
3.3. The properties of the filter
Property 1: This new filter is self-adaptive, because this filter works in time domain and the decomposition process is based on the characteristic of the signal itself. When we design this new filter, the interpolation method, the orders of noise and the length of filter window are priorities need to be considered, the frequency of the signal and noise is no longer the main parameters for the design of this filter.
Property 2: The phase delay of this new filter is fixed. For the traditional digital filter, the phase delay changes with the change of input signal’s frequency. If the central point of the filtered data is taken as the result of the filter and the data length is . The data in filter window is , at next sampling time the data will change to , when sampling point moves to the center of filter window, the data becomes . So the phase delay is , where is the sampling time. It’s clear that the phase delay is not related to the frequency of the input signal, and only related to data length and sampling time .
Fig. 11The decomposition result when the window length is 20
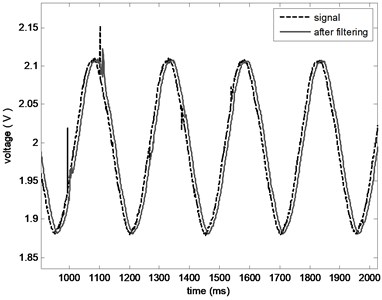
Fig. 12The decomposition result when the window length is 50
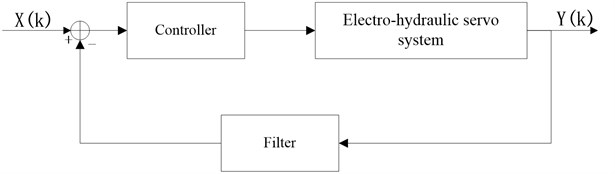
4. The design of controller
4.1. The compensation of phase delay
The picture of practical object and the control block diagram of electro-hydraulic servo system are shown in Fig. 13 and Fig. 14, respectively. The presence of the filter in feedback will have some influences on amplitude and phase. The phase delay of traditional filter like Butterworth filter and Chebyshev filter always grows larger while frequency becomes higher. But the phase delay of this new improved HHT filter is only related to the length of filtering window , and maintains sampling periods delay. Based on this feature, the phase delay could be compensated in controller.
Fig. 13The picture of the practical object

Fig. 14The system block diagram
This electro-hydraulic servo system is a position control system, and its transfer function can be obtained by using system identification. The form of transfer function is shown in Eq. (13):
in which , . in Eq. (13) shows that there is a orders delay in system. To compensate this delay, the input becomes , and then the change of output is shown in Eq. (14):
After compensation, the phase delay is only related to system itself.
4.2. Stability analysis of controller
The property 2 of this new filter means that a delay link is added to the system. The system’s open loop transfer function will be changed from to . If the input signal is , then the output signal with noise is:
The noise after filtering becomes , , is the error between original noise and filtering result. Because the real filter cannot achieve the ideal effect, the error always exists. The system’s output after filtering is , . So this new controller’s stability is only related to system itself, and does not introduce additional stability influence.
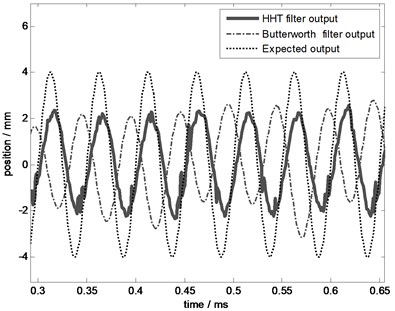
Fig. 15The effect comparison chart at 2 Hz
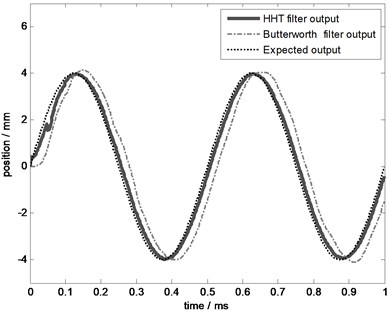
Fig. 16The effect comparison chart at 5 Hz
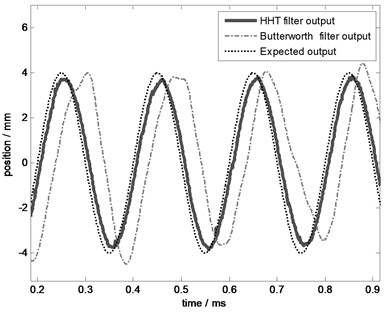
4.3. The control result
Apply this new controller in system and test the control performance at frequency 2 Hz, 5 Hz, 10 Hz, and 20 Hz. To illustrate the practicability and the superiority of this new controller, take Butterworth filter (Low pass filter, with pass band 0-20 Hz, pass band attenuation no more than 3 dB, the attenuation of 150 Hz at least 60 dB) as a comparison filter. The comparison results are shown in Figs. 15-18, illustrating that the control error of this new filter is less than Butterworth filter especially at high frequency.
Fig. 17The effect comparison chart at 10 Hz
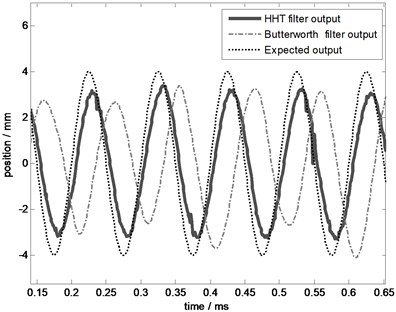
Fig. 18The effect comparison chart at 20 Hz
5. Conclusions
To design a new on-line filter based on HHT method, optimization of EMD method from four aspects are made and a better filtering performance is obtained. These optimizations are used to improve the effect of envelop curve which is the key of decomposition process. A new controller based on this new filter is also designed. Due to the self-adaptation characteristics of HHT method, the new controller’s phase delay is only related to the filtering window length , and this delay could be compensated in controller. The control effect has been improved and more accurate control results are achieved.
References
-
Wang Linhong, Wu Bo, Du Runsheng, et al. Nonlinear dynamic characteristics of moving hydraulic cylinder. Journal of Mechanical Engineering, Vol. 43, Issue 12, 2007, p. 12-19, (in Chinese).
-
Huang N. E., Shen Z., Long S. R., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London Series A. Vol. 454, 1998, p. 903-995.
-
Ramandeep Kaur, Vikramjit Singh Time-frequency domain characterization of stationary and non-stationary signals. International Journal for Research in Applied Science and Engineering Technology, Vol. 2, Issue 5, 2014, p. 438-447.
-
Antonio H. C., Stephan H. Adaptive time-frequency analysis based of autoregressive modeling. Signal Processing, Vol. 91, Issue 4, 2011, p. 740-749.
-
Fleureau J., Nunes J. C., et al. Turning tangent empirical mode decomposition: a framework for mono and multivariate signals. IEEE Trans on Signal Processing, Vol. 59, Issue 3, 2011, p. 1309-1316.
-
Marcus D., Torsten S. Performance and limitations of the Hilbert-Huang Transform (HHT) with an application to irregular water waves. Ocean Engineering, Vol. 31, 2004, p. 1783-1834.
-
Yang Pei-hong, Yue Li-hai, Kang Lan, et al. Study on HHT based low frequency oscillation monitor for power system. Electrical Measurement and Instrumentation, Vol. 51, 21, p. 110-114, (in Chinese).
-
Lu Zhi-mao, Jin Hui, Zhang Chun-xiang, et al. Voice activity detection in complex environment based on Hilbert-Huang transform and order statistics filter. Journal of Electronics and Information Technology, Vol. 34, Issue 1, 2012, p. 213-217, (in Chinese).
-
Park J. H., Lim H., Myung N. H. Analysis of jet engine modulation effect with extended Hilbert-Huang transform. Electronics Letters, Vol. 49, Issue 3, 2013, p. 215-216.
-
Jie Huang, Jian Tang, Meijun Zhang, et al. An improved EMD based on cubic spline interpolation of extremum centers. Journal of Vibroengineering, Vol. 17, Issue 5, 2015, p. 2393-2409.
-
Li Zhao, Zhou Xiao-jun, Xu Yun End effect treatment for EMD based on the period superposition extrapolation of mean generating function. Journal of Vibration and Shock, Vol. 32, Issue 15, 2013, p. 138-143, (in Chinese).
-
Guo Ming-wei, Ni Shi-hong, Zhu Jia-hai, et al. HHT/EMD end extension method in vibration signal analysis. Journal of Vibration and Shock, Vol. 31, Issue 8, 2012, p. 62-66, (in Chinese).
About this article
Jing Huang performed the experiments and data analyses, wrote the manuscript. Changchun Li contributed to the conception of the study. Hao Yan helped with constructive discussions. Xuesong Yang helped perform the analysis. Jing Li contributed to manuscript preparation.
