Prognostic diagnosis of the health status of an air-turbine dental handpiece rotor by using sound and vibration signals

1. Introduction

Air-turbine dental handpieces (ATDHs) have been widely used in dentistry for many years. When ATDH components malfunction, additional compressed air is required to achieve a suitable pressure level when performing in vivo surgery. The need for additional compressed air to drive the rotor is associated with the malfunction of ball bearings resulting from changes in axial or radial bearing preload. Consequently, friction causes an increase in temperature, which is transferred to the mandrel of the rotor head. This increased temperature is hazardous to the nerves in human teeth. Therefore, this study proposed a prognostic method for clinicians to determine the status of ATDHs.

Dyson and Darvell [1] studied the air flow and free-running speed characteristics of ATDHs to test ATDH for defects or malfunction. A visual inspection for damage indicated that the rotors operated freely with no obvious catches, and no discontinuity was observed in the speed-pressure response (i.e., no obvious imbalance). Wei et al. [2] studied various factors influencing ATDH bearing-failure, including loading, lubrication, and corrosion protection. Poole et al. [3] used a scanning-laser vibrometer to examine the vibrations of unloaded turbines and speed-increasing handpieces. The results showed that vibrations contributed to the symptoms of hand-arm vibration syndrome in clinicians and iatrogenic enamel cracking in teeth. Ruth Louise [4] used laser Doppler for the measurements of electric and Air dental handpiece vibration at different measuring points. Experimental results showed the vibration amount difference with no load is about 0.004 mm. There was no significant difference when the measuring points is changes along the dental handpiece. Vahid Zakeri [5] used the accelerometer (contact sensor) and laser Doppler vibrometer (non-contact) to measure the vibration signals for distinguishing the tooth layer, and they found that using vibration signals from two instruments are not much different. In this study, the examined ATDH was equipped with a rolling-element bearing with ceramic bearing balls to balance the rotor and an O-ring for radial resilience, and thick spring washers for axial loading. When examining free-running or dental cutting procedures, both the radial and axial loads on the rotor jointly are used to determine the output speed performance or health status of a device.

Recently, numerous strategies have been proposed for diagnosing the operational status of mechanical devices, which can provide critical information for extending the lifespan of devices or indicating when key components should be replaced. Systems that capture and analyze sound and vibration signals corresponding to various machine states can facilitate the development of diagnostic models. Preloading effectively increases the stiffness of precision-burring drills, thereby maximizing their efficiency. Preload loss or part failure leads to a lower natural frequency, lower stiffness, oscillatory positioning, and the potential for rapid device failure during surgery. For most acquired signals, fault diagnosis is performed with conventional Fourier transforms in the frequency domain. However, in numerous real applications, signals are composed of multiple components and are typically distorted by noise. Huang et al. [6] developed a novel signal-analysis approach. The approach was defined based on the concepts of instantaneous amplitude, phase, and frequency, such that the original signal can be expressed in terms of a Fourier-like expansion. Yan et al. [7] presented a signal analysis technique for machine health monitoring based on the Hilbert-Huang Transform (HHT). The analytical background of the HHT [6] is introduced, based on a synthetic analytic signal, and its effectiveness was experimentally evaluated using vibration signals measured on a test bearing. The results demonstrated that HHT is suited for capturing transient events in dynamic systems such as the propagation of structural defects in a rolling bearing, and thus providing a viable signal processing tool for machine health monitoring. Lotfi et al. [8] proposed a joint method for detecting bearing signals, called bi-spectrum based EMD (BSEMD). The original vibration signals was collected from accelerometers and then decomposed by EMD and a set of IMFs was produced. Then, the IMF signals were analyzed via bi-spectrum to detect the outer race bearing defects. Such procedure was illustrated with the experimental bearing vibration data. In their experimental results BSEMD techniques can effectively diagnosis bearing failures. Wang. et al. [9] proposed a new method to identify compound faults from measured mixed-signals, which is based on ensemble empirical modem decomposition (EEMD) method and independent component analysis (ICA) technique. Experimental results validate the effectiveness of proposed method in compound fault separating, which works not only for the outer race defect, but also for the rollers defect and the unbalance fault of the experimental system. Soualhi et al. [10] proposed a new approach that combines the HHT, the support vector machine (SVM), and the support vector regression (SVR) for the monitoring of ball bearings. They used the HHT to extract new heath indicators from stationary/nonstationary vibration signals and was able to tack the degradation of the critical components of bearings. Yu et al. [11] used the HHT for discrimination the normal and defective gear. They further classified the gear failure modes into crack fault and broken teeth. Igarashi et al. [12] investigated the sound reduction of a ball screw using sound pressure level measurement and real-time frequency analysis. Anna et al. [13] used microphone for the analysis of an industrial gear hobbing machining process and induced vibration disastrous limitations in tool life.

Since the Hilbert-Huang transform provides both time and frequency analysis methods for various engineering applications. Accordingly, clinicians or technicians can benefit from its ability to predict the lifespan and health status of ATDH rotors; however, few studies have focused on this topic. The complexity of a rotor under dynamic preload conditions or bearing failure is highly nonlinear and nonstationary. Traditional entropy measurements involve quantifying only the regularity (predictability) of a time-series data set by using a single scale. No obvious correlation exists between regularity and complexity.

This study employed a multiscale entropy (MSE) analysis tool [14] to measure the complexity of finite-length time-series data of an ATDH being operated for 30 seconds. The MSE computational tool was successfully applied to both physical and physiological data sets, and it is suitable for various measures of entropy. An MSE-based framework was developed for studying biological systems by using a statistical physics approach to obtain a practicable measure for quantifying dynamic complexity. Complex feature patterns of a rotor under normal, preloaded, and bearing failure conditions were determined and abstracted through the MSE tool, and MSE values were analyzed to discriminate the prognostic status of rotor. Based on complexity of mechanical concepts, changes in the characteristics of the ATDH rotor status were monitored through simulation involving the fast Fourier transform (FFT), HHT, and MSE methods.

2. Experiment setup and results

In general, for an ATDH, the specification of the dynamics of a balanced rotor and preload of a ball-bearing are selected and determined a priori. In this study, the normal preload conditions were determined based on the standard (original) design preload of a typical dental surgical device used in clinical applications. A spring washer was added in the axial direction to test the ATDH under preload conditions by increasing the mechanical friction, force on the ball trace, and stiffness. The tested ATDH (Tiger 201-3T, Thunder Tiger Corp., Taiwan) was equipped with a mandrel with a diameter and length of 1.6 and 19 mm, respectively. Fig. 1 shows a schematic diagram of the ATDH. Fig. 2 shows an image of a bearing with a damaged outer race; the figure also indicates the location and length of a scratch. Fig. 3 shows an image of the in-house ATDH measurement platform, comprising a laser-Doppler velocity meter (Label 1), condenser microphone (Label 2; the distance from the device is indicated by a ruler on the table surface), ATDH (Label 3), standard air-controller platform (Label 4), and data-acquisition system (Label 5). The laser-Doppler velocity meter (brand of Metro Laser, Inc., VibroMet Model 500) with velocity range of 5 μm/s to 800 nm/s was acquisitioned and interfaced by Labview^TM system for rotor speed calculation. To make more precise measurement signal, an additional sticker can be attached to the surface of ATDH when the laser spot light is vague. The condenser microphone of a sound analyzer (brand of SVANTEK, Svan949) carrying the highest sampling frequency of 48 kHz and frequency response of 0.8 Hz to 20 kHz was used for acoustic measurement. A mobile MEMS microphone featured with size of 4×3×1 mm, highest sampling frequency of 194 kHz and frequency response ranging from 100 Hz to 18 kHz was used with the same measuring conditions of condenser microphone. Though a standard air-controller platform (Label 4 of Fig. 3) is conventional used in dental clinics, an additional single value pressure controller (brand of Alicat, PC3 series) was used in experiment to control the good quality of the compressed air pressure. The valve featured with Proportional-Integrated-Derivative controller can reach the feedback response time of 100 ms that makes the experiment with more accuracy.

Fig. 1Illustration for the schematic diagram of the ATDH: 1. Spindle (test mandrel), 2. Spring washer, 3. O-ring, 4. Ball bearing, 5. Blades

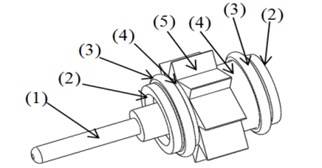
Fig. 2Picture of the damaged outer race bearing with indicated scratch and measured length

Fig. 3Picture of in-house ATDH measurement platform

Fig. 4Experiment of the dB sound by measured distance from 1.5 cm, 15 cm and 30 cm, respectively for healthy (with solid line) and bad bearing (with dashed line) dental handpieces

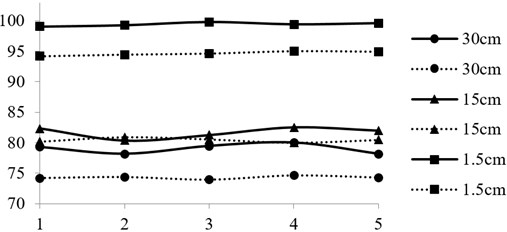
When measuring sound waves in decibels, as shown in Fig. 4, it is difficult for the human ear to determine the health status of an ATDH. The decibel level produced by a faulty bearing is invariably lower than that of a healthy bearing at distances of 1.5, 15, and 30 cm. Fig. 5 shows the FFT spectrum of the vibration frequency captured using the laser-Doppler vibration measurement when the laser was aimed at the head of the ATDH. The frequency identified in the figure corresponds to the ATDH’s axial rotation frequency. The experimental results showed that the characteristic frequency was lower when the ATDH was equipped with additional axial preload spring washers or when the ball bearing was faulty (i.e., the outer race was scratched). The ball pass frequency of the outer race (BPFO) in Fig. 5(b) is clearly observable in the frequency spectrum.

Fig. 5FFT spectrum of the vibration frequency captured using the laser-Doppler vibration measurement

a) FFT of the normal ATDH’s axial spinning frequency (Fr) with 5.6kHz when supplied air is 40 psi

b) FFT of the preloaded ATDH’s axial spinning frequency (Fr) with 5.4 kHz when supplied air is 40 psi with additional axial washers

Fig. 6 also shows the FFT spectrum of the axial rotation frequency of the ATDH when the supplied air pressure was set at 20 psi. The dynamic frequencies in Fig. 6(c) indicate the mechanical complexity and richness in low-frequency content when the faulty bearing status caused vibration to propagate through the rotor blade, test mandrel, and then to the head of the ATDH. The respective characteristic axial rotation frequencies at 20, 30, and 40 psi are 4.8, 5.2, and 5.6 kHz (under normal conditions); 4.5, 5.0, and 5.4 kHz (with additional axial washers); and 0.465, 0.79, and 1.5 kHz (when the health status of the bearing is poor), respectively. The figure shows that the characteristic frequencies are lower when the air pressure is reduced.

Fig. 6FFT spectrum of the axial rotation frequency of the ATDH

a) FFT of the normal ATDH’s axial spinning frequency (Fr) with 4.8 kHz when supplied air is 20 psi

b) FFT of the preloaded ATDH’s axial spinning frequency (Fr) with 4.5 kHz when supplied air is 40 psi with additional axial washers

c) FFT of the bad bearing in the outer race of ATDH’s axial spinning frequency (Fr) with 0.465 kHz when supplied air is 20 psi

In this study, an ATDH was operated at 20, 30, and 40 psi under three distinct operating conditions (i.e., normal, with additional preload spring washers, and with a faulty bearing) without water-injection cooling. The temperature distribution of the ATDH and the effects of the faulty rotor bearing on the drill were investigated while operating the device in vivo. Fig. 7 shows thermal images indicating the temperature distribution of the ATDH. The figure shows that the faulty bearing caused the drill temperature to increase. The experimental results show that the ATDH exhibited predominately high temperatures while drilling (placement of the test mandrel) because of friction from the faulty bearing. The temperatures increased rapidly (within 5 seconds) at high speeds (40 psi) without water-cooling injection. Fig. 7 (from left to right) shows an image of the laboratory setup, a thermal image of the healthy ATDH, and a thermal image of the unhealthy ATDH. At an ambient temperature of 24 °C to 25 °C, the peak temperature of the healthy ATDH was 38.1 °C (without the water cooling system) when acrylic cutting was simulated. The thermal image of the unhealthy ATDH (Fig. 7, right side) shows that the temperature of the drill peaked at 78.3 °C because of the friction from the ball bearing, which was then transferred to the drill when acrylic cutting was simulated. The increase in temperature was primarily caused by friction among the ball bearing, bearing race, and rotor blade. As shown in Fig. 7, a lack of water cooling during the 5-second cutting operation had a strong impact on the temperature distribution of the ATDH. In summary, the difference in decibel levels (Fig. 4) is difficult to discern when the measurement is performed at a distance of 15 cm, which is the ISO standard. Consequently, the prognostic diagnosis of the healthy or preload status was indistinguishable. This is critical because knowing the frequency dynamic response of the ATDH can indicate whether each ball bearing is healthy.

Fig. 7Picture and thermo camera images of the temperature distribution of the dental handpiece with acrylic cutting when operated in 5 seconds without water cooling

a)

b)

c)

3. The Multi-Scale Entropy Method and Its Diagnostic Application

An MSE-based framework was developed in [15] for studying biological systems by using a statistical physics approach to obtain practicable measures for quantifying dynamical complexity. As stated, MSE analysis is a method for measuring the complexity of finite length time series. This computational tool is applied here with a variety of measures of entropy. In this paper, entropy uses the sample entropy (SampEn) measure [15]. SampEn is a refinement of the approximate entropy [16] family of statistics. The acquisitioned laser doppler vibrometer, condenser microphone and mobile MEMS microphone signals data will be processed by MSE.

The MSE method incorporates two procedures. A “coarse-graining” process is applied to the time series. For a given time series, multiple coarse-grained time series are constructed by averaging the data points within non-overlapping windows of increasing length, $\tau$ as shown in Fig. 8.

Fig. 8Schematic illustration of coarse-graining procedure for Scales 2 and 3

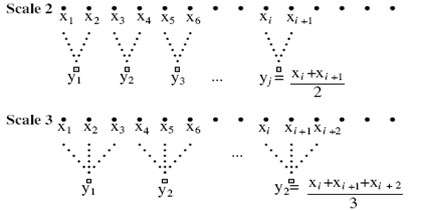
Each element of the coarse-grained time series, $y_j^{\left(\tau \right)}$, is calculated according to Eq. (1):

where $\tau$ represents the scale factor and $1\le j\le N/\tau$. The length of each coarse-grained time series is $N/\tau$. For Scale 1, the coarse-grained time series are simply the original acquisitioned signals $X_i$ as follows.

Let $\left\{X_i\right\}=\{x_1,\dots ,x_i,\dots ,x_N\}$ represent a time series of length $N$. Consider the $m$-length vectors: $u_m\left(i\right)=\left\{x_i,x_{i+1},\dots ,x_{i+m-1}\right\}$, $1\le i\le N-m+1$. Let $n_i^m\left(r\right)$ represent the number of vectors $u_m\left(j\right)$ that are close to the vector $u_m\left(i\right)$, i.e., the number of vectors that satisfy $d\left[u_m\left(i\right),u_m\left(j\right)\right]\le r\text{,}$ where $d$ is the Euclidean distance. $C_i^m\left(r\right)=n_i^m\left(r\right)/\left(N-m+1\right)$ represents the probability that any vector $u_m\left(j\right)$ is close to the vector $u_m\left(i\right)$ [14].

The MSE value is calculated as following equation:

The SampEn is calculated for each coarse-grained time series, and then plotted as a function of the scale factor. SampEn is a “regularity statistic” that “looks for patterns” in a time series and quantifies their degree of predictability or regularity.

Fig. 9Illustration of time data by applying SampEn [14]

In Fig. 9, a time series $u\left[1\right]$,…, $u\left[n\right]$ is shown to illustrate the procedure for calculating sample entropy. Dotted horizontal lines around data points $u\left[1\right]\text{,}$$u\left[2\right]\text{,}$ and $u\left[3\right]$ represent $u\left[1\right]\pm r$, $u\left[2\right]\pm r$, and $u\left[3\right]\pm r$, respectively. All green points represent data points that match the data point $u\left[1\right]$. Similarly, all red and blue points match the data points $u\left[2\right]$ and $u\left[3\right]$, respectively. The segment shown in Fig. 2 involves two green-red sequences, ($u\left[13\right]$, $u\left[14\right]$) and ($u\left[43\right]$, $u\left[44\right]$), that match the template sequence ($u\left[1\right]$, $u\left[2\right]$), but only one green-red-blue sequence that matches the template sequence ($u\left[1\right]$, $u\left[2\right]$, $u\left[3\right]$). Therefore, in this case, the number of sequences matching the 2-component template sequences is two and the number of sequences matching the 3-component template sequence is 1. These calculations are repeated for the next 2-component and 3-component template sequence, which are, ($u\left[2\right]$, $u\left[3\right]$) and ($u\left[2\right]$, $u\left[3\right]$, $u\left[4\right]$), respectively. The numbers of sequences that match each of the 2- and 3-component template sequences are again counted and added to the previous values. This procedure is then repeated for all other possible template sequences, ($u\left[3\right]$, $u\left[4\right]$, $u\left[5\right]$),…, ($u\left[N-2\right]$, $u\left[N-1\right]$, $u\left[N\right]$), to determine the ratio between the total number of 2-component template matches and the total number of 3-component template matches. SampEn is the natural logarithm of this ratio and reflects the probability that sequences that match each other for the first two data points will also match for the next point. Therefore, the higher entropy indicates the irregularity and complexity for interested time series data. Here, the viewpoints of preloaded spring and bad outer race ATDHs should produce a variety of measures indicating the complexity with high entropy value. The embedded irregularity and complexity of the ball screw describe the nonlinear dynamics when its preload is lost. Intuitively, complexity is associated with meaningful structure richness incorporating correlations over multiple spatiotemporal scales. Preload effect and bad outer race developments should exhibit phenomena of more random contact force between balls with running race and more irregular force manner in between the balls and ball nut during motion.

4. Experimental results

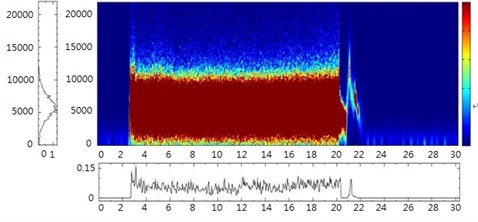
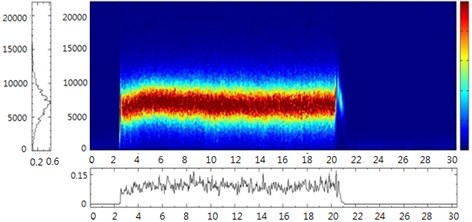
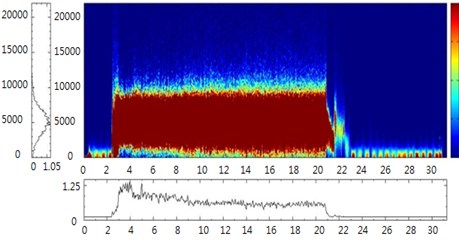
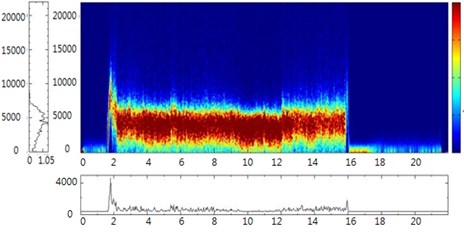
In this study, HHT and MSE calculations were performed using Visual Signal Version 1.3 (AnCAD Inc., Taiwan). Based on the concept of mechanical complexity, the health states of the ATDH were determined and abstracted through HHT and MSE simulations. The HHT spectrograms in Figs. 10 and 11 show the ATDH frequency patterns in the time domain, which were captured using the condenser microphone and portable microelectromechanical system (MEMS) microphone, respectively. The figure shows that small peaks occurred at low frequencies, particularly where the air supply was disconnected at 20 seconds. These phenomena indicated the vibration mode of a normal rotor inducing fluctuations in air pressure and sound, originating from impacts occurring inside the ATDH head chamber and propagating to the outlet of the test mandrel. When the rotor’s air supply was suddenly disconnected, the captured air frequency decreased rapidly from high to low and then to zero under normal conditions. The vibration mode of the rotor was successfully induced when using a healthy ATDH, followed by low-frequency modes in the time-frequency spectrum. By contrast, few low-frequency peaks appeared in the spectrogram after 20 seconds when the health status of the ATDH bearing was poor because the air circulating around the rotor did not induce vibration modes when the supply air was disconnected. In comparison to the sound signals after 20 seconds (Fig. 8), Fig. 9 shows identical results when the condenser microphone was used instead of the portable MEMS microphone. The experimental results indicated that this is a convenient and inexpensive solution for diagnosing the health status of ATDHs.

Fig. 10a) HHT plot of the normal ATDH and b) bad outer race ATDH by condenser microphone measurement

a)

b)

SampEn [16], which is a regularity statistic for identifying patterns in time-series data and quantifying the degree of predictability or regularity, was calculated for each coarse-grained time-series data set, and subsequently plotted as a function of the scale factor. SampEn is the natural logarithm of this ratio, and it reflects the probability that two matching consecutive data points also match the subsequent data point. Therefore, a higher entropy value indicates irregularity and complexity in a time-series data set. A normal ATDH should yield various measures indicating complexity at high entropy values. The embedded irregularity and complexity of the pressurized air outlet indicates the nonlinear dynamics of the ATDH when its vibration and sound mode are measured. Intuitively, complexity is associated with rich meaningful structures incorporating correlations over multiple spatiotemporal scales. Healthy ATDHs should exhibit stronger vibration forces between the ball bearing and bearing race, as well as complex outlet air-pressure forces as the air enters the atmosphere while the test mandrel is rotating.

Fig. 11a) HHT plot of the normal ATDH and b) bad outer race ATDH by mobile MEMS microphone measurement

a)

b)

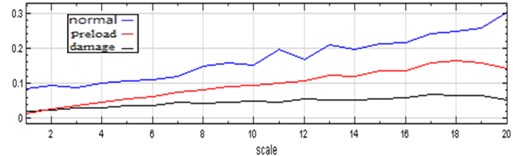
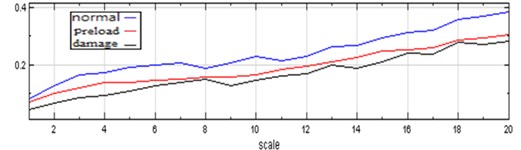
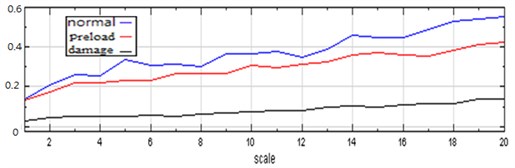
Fig. 12 shows the MSE plots from one of the 10 experiments involving the ATDH under the three discussed test conditions. As mentioned, the MSE value should be higher under normal conditions. Because complex sound pressure levels shown in the spectrogram are related to the actuated air interacting with rotor and dental drill (i.e., the test mandrel), the unhealthy ATDH yielded a decrease in MSE values when the measurements were performed using the laser-Doppler vibrometer, condenser microphone, and mobile MEMS microphone.

The experimental results show that higher MSE values indicate a high degree of entropy, which caused the ball bearing for the turbine rotor-blade to spin faster when the air pressure was increased. Consequently, this yielded a high complexity index, which corresponds to the mechanical complexity hypothesis associated with rich structures and sound responses. Intuitively, as the preload conditions create, both the rotor blade inside the ATDH chamber and the bearing race of the ball bearing create additional rolling contact, along with increased random vibration motion and irregularity, although the ATDH releases less energy output compared with that observed under other test conditions. Under poor rotor conditions, particularly when the outer race was scratched, the test mandrel was driven by a less-dynamic flow of energy circulating through the bearing race. The experimental results indicated that the MSE value of the healthy ATDH was higher than that of the preloaded ATDH when it was operated for 30 seconds.

In summary, the proposed method enables manufacturers and clinicians to evaluate the health status of an ATDH rotor by using a condenser or MEMS microphone and a personal computer. The proposed technique can be implemented in the simplest way as follows. In practical experimentation and industrialization, one can drive the ATDH, perform the vibration or acoustic data acquisition by 30 seconds via the vibration or mobile MEMS microphone instrument, and then calculate the Multi Scale Entropy (MSE) through the cloud system.

The experimental results indicated that the approach is a promising prognostic tool for monitoring the health status of ATDH rotors in dental clinics and industrial applications. The method offers an inexpensive, robust, and reliable technique for diagnosing the health status of an ATDH by analyzing the sound or vibration signals, and it can be easily integrated into diagnosis processes in manufacturing products. An automatic fault identification strategy which could be specially adapted to the particular air turbine can be implemented in practice.

Fig. 12MSE plots of using laser doppler vibrometer, condenser microphone and mobile MEMS microphone for normal, axial preloaded spring and bad outer race ATDHs for 30 seconds computation

5. Conclusion

In this study, signal analysis techniques were employed to detect the health status of an ATDH rotor used in clinical practice. The highly nonlinear processing of HHT and MSE methods were applied to diagnose the health status of the studied ATDH. A computational measure of MSE was used to dynamically quantify the complexity of the ATDH and identify changes in the health status of the device. A laser-Doppler vibrometer, condenser microphone, and portable MEMS microphone were used to extract vibration or audio signals to determine the rotor state by observing patterns in an HHT spectrogram. Subsequently, the vibration signals and audio frequencies were distinguished based on the HHT patterns and MSE values, thereby yielding practicable MSE measures indicating the health status of the ATDH. The experimental results showed a clear inclination toward complexity when the ATDH exhibited a healthy status under constant air pressure. The results also showed that the proposed method can be employed to determine the prognosis of a rotor while using the ATDH.