Study on a novel fault diagnosis method based on information fusion method

3.1. Quantum particle swarm optimization(QPSO) algorithm

The PSO algorithm is a population-based search algorithm. It consists of a number of individuals, which have one position and one velocity and are denoted as particles. Sun et al. [29] proposed a quantum particle swarm optimization(QPSO) by researching the convergence behavior of the particles from the perspective of quantum mechanics. The QPSO algorithm improved the evolutionary search strategy of the PSO algorithm. This algorithm only needs the velocity vector for finding the global optimal solution. The QPSO algorithm is far superior to the all developed PSO algorithms for the search ability.

In the QPSO algorithm, each particle must converge on the respective random point $P$, $P=(p_1,p_2,\cdots ,p_n)$, the $j$th dimension of the $i$th particle is described as follow:

A global point is introduced into the PSO algorithm to calculate the next iteration variable of the particle, which is defined as the mean best value of the local optimum position in all particles. The calculated expression is described as follows:

where $M_{best}$ is the intermediate position in the $P_{best}$, $M$ is the number of the particles, $j$ is dimension value of the particle, $P_i$ is the best position of the particle, $P_{ij}$ is the found optimal solution ($P_{best}$) of the particle, $P_{gj}$ is the found optimal solution ($G_{best}$) of all particles, $x_i\left(t\right)$ is the related position information. $\beta$ is the contraction or expansion coefficient, $r_1$, $r_2$ and $u$ are the random number in the [0, 1].

In the QPSO algorithm, the particle state is only described by the position vector, and there is only one control parameter $\beta$. The control of parameter $\beta$ is very important, because the parameter $\beta$ determines the convergence speed of the algorithm. When the QPSO algorithm is used to solve the practical problems, there are several control methods for parameter $\beta$. The best simple one is that the parameter $\beta$ is set to be a fixed value in the running. But this method is lack of robustness. The other efficient method is linear decreasing strategy that linearly decreases the value of parameter $\beta$. This method has achieved very good results in the specific practical problems [30]. So the linear decreasing strategy is used to determine the value of parameter $\beta$ in this paper. The expression of the linear decreasing strategy is described:

where $t$ is the current number of iterations, $t=$ 0, 1, 2,…, $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$. $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum number of iterations and the value of parameter $\beta$ is from 1 to 0.5.

3.2. Chaos optimization algorithm

Chaos optimization algorithm (COA) [31] is a population-based stochastic optimization algorithm by using the chaotic map. In the COA, it searches all points in turn within changing range of variables, and selects the better point as the current optimum point. Then the current optimum point is regarded as the center, a tiny chaotic disturbance is imposed and a careful search is performed for searching the global optimal point with the high probability. The COA with the refined search space, better search speed and higher search accuracy is selected to optimize QPSO algorithm in this paper. The COA is used to get chaotic variables. So Logistic chaotic model is used to generate the chaotic variable. The mapping equation is given:

where control variable ($\mu \in [0,\mathrm{}4]$) is the parameter of Logistic. When control variable is $\mu =$ 4, Logistic mapping is fully mapped in [0, 1] and it is in the chaotic state. It takes on the traversal between [0, 1], and any state will not repeat. Under Logistic mapping function (the initial condition $x_0$), the generated sequences are not periodic and must converge to the specific value outside the given range.

3.3. Support vector machine (SVM)

The SVM is one of the popular tools for supervised machine learning method based on structural risk minimization [32-34]. The characteristic of SVM is to map the original nonlinear data into higher-dimensional feature space. The given training sample is $S=\left\{\right(x_i,y_i\left)\right|i=1,\mathrm{}2,\mathrm{}3,\dots ,m\}$, $m$ is the number of samples, the set $\left\{x_i\right\}\in R_n$ represents the input vector, $y\in \{-\mathrm{1,1}\}$ indicates the corresponding desired output vector, the input data is mapped into the high dimensional feature space by nonlinear mapping function $\varphi (•)$. The optimal classification hyperplane must meet the following conditions:

where $\omega$ is Omega vector of super plane, $b$ is offset quantity. Then the classification decision function is described:

The SVM model is described by the optimization function $\underset{\omega ,\xi ,b}{\mathrm{m}\mathrm{i}\mathrm{n}}J(\omega ,{\xi }_i)$:

where ${\xi }_i$ is slack variable, $b$ is offset, $\omega$ is support vector, $\xi =({\xi }_1,{\xi }_2,\cdots ,{\xi }_m)$, $\gamma$ is classification parameter for balancing the fitting error and model complexity.

The optimization problem transforms into its dual space. Lagrange function is used to solve. The corresponding optimization problem of the SVM model with Lagrange function is:

where ${\alpha }_i$ is the Lagrange multiplier, and ${\alpha }_i\ge 0$ ($i=$1, 2, 3,…, $m$).

The classification decision function is described:

4.1. Chaos quantum particle swarm optimization (CQPSO) algorithm

The QPSO algorithm has better global search ability than the PSO algorithm. But it still exists the premature convergence problem and is easy to fall into the local optimum value. So the determining mechanism of premature convergence is used to avoid the local optimal value:

where $f_i$ is the fitness value of current particle, $f_{best}$ is the best fitness value of current particle, $f_{worst}$ is the worst fitness value of current particle. With the increasing of iteration, the value of the $P_i$ is decreasing.

The COA method takes on the refined search space, better search speed and higher search accuracy. So a new chaos quantum particle swarm optimization (CQPSO) algorithm based on combining the QPSO algorithm with the chaos method is proposed to improve the convergence speed and convergence precision. In the CQPSO algorithm, Logistic chaotic model is used to generate the chaotic variables, which perturb some particles in order to enhance the local search ability and improve the search accuracy. The flow of the CQPSO algorithm is described:

Step 1. Initialize.

The related parameters and the termination condition are initialized. The $x\left(t\right)$ is different initial value of the number $i$. The chaotic variables are generated according to Eq. (6).

Step 2. The parameter $\beta$ linearly decreases from 1 to 0.5 with the increasing of iteration.

Step 3. Map $x(t+1)$into the space domain:

Step 4. Calculate the fitness value.

According to the selected fitness function, the fitness value is calculated. The individual extremum value ($P_{{}_{\mathrm{}}{}^{best}\mathrm{}}$) and global extremum value ($M_{best}$) are searched and updated.

Step 5. For each particle, the fitness value of the particle is compared with the fitness value of extremum point, and the population is updated.

Step 6. Determine whether the operation will end. The calculation result meets the end condition, then the operation will end. And the obtained result is output. Otherwise go to step 7.

Step 7. Determine the global extremum value ($M_{best}$). If the $M_{best}$ is not continuously updated, the COA is executed for the best particle in the population. Then go to step 8.

Step 8. The new particle is generated. Go to step 3. to continue the implementation of the CQPSO algorithm.

4.2. Information fusion method

In the SVM, the kernel function is used to map the input into the high-dimensional feature space to find the optimal superplane. So the kernel function must meet the expression:

For fault diagnosis, because the radial basis kernel function takes on better smoothness and analyticity, it is widely applied in the SVM. So the radial basis function is selected as the kernel function of the SVM. Its expression is described as follow:

where $x$ is a $m$-dimensional input vector, $x_i$ is the center of the $i$th radial basis function.

In the SVM, the kernel parameter $\sigma$ is used to determine the corresponding relation between the mapping function and feature space. It is a very important to select the appropriate value of the $\sigma$ for the feature space. The penalty coefficient $C$ is used to adjust the proportion of the confidence range and experience risk for obtaining the best learning ability. The penalty coefficient $C$ is smaller or larger value, it will cause the poor generalization ability. So it is very critical and difficult to determine the optimal values of the $\sigma$ and $C$ in the SVM. The COA takes on the advantages of the refined search space, better search speed and higher search accuracy, the QPSO algorithm takes on the global optimization ability. So the COA is used to better initialize the parameters of the QPSO algorithm to propose the CQPSO algorithm. Because the proposed CQPSO algorithm takes on stronger global optimization ability in the feasible solution space, it is used to optimize the $\mathrm{\sigma }$and $C$ in order to obtain the optimal value combination of the $\sigma$ and $C$ for constructing a high-precision SVM model (called information fusion (CQPSM)method) with the higher accuracy and stronger generalization ability.

The process of optimizing parameters of the SVM is described in detail: the $\sigma$ and $C$ of the SVM is selected as combinatorial optimization problem to establish the objective function. Then the CQPSO algorithm is used to search the optimal values of the objective function in order to find out the optimal parameter combination. Firstly, the fitness function is defined:

where $RMSE$ is root mean squared error, $M$ is the number of training samples, $f\left(i\right)$ is the actual value of the $i$th sample, $f^{\mathrm{\text{'}}}\left(i\right)$ is the predicted value of the $i$th sample. The parameter combination with the minimum $RMSE$ is selected. The objective function is described:

The function $f$ is objective function. The CQPSO algorithm is used to exhaustively search in the domain of $C$ and $\sigma$ in order to let the objective function $f$ to converge to its minimum value. At this time, the values of $C$ and $\sigma$ are the optimal parameter combination of the SVM.

The flow chart of the CQPSM is shown in Fig. 1.

Fig. 1The flow chart of the CQPSM method

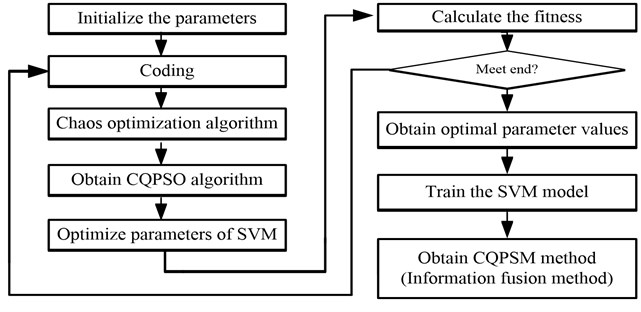
The steps of the CQPSM are described:

Step 1. Initialize.

The initial parameters include population size ($X\left(t\right)=\{x_1,x_2,\cdots ,x_m\}$), learn factors ($c_1$ and $c_2$), initial control parameter ${\beta }_0$, $r_1$, $r_2$ and $u$, the maximum iteration ($T_{\mathrm{m}\mathrm{a}\mathrm{x}}$), and the current iteration ($t=\text{1}$). Randomly initialize the velocity and position of each particle in the given range. The position of each particle is defined in $x_i\in [-\mathrm{1,1}]$.

Step 2. Code for the parameters.

When the CQPSO algorithm is selected to optimize parameters ($C$ and $\sigma$), each particle is obliged to be replaced by a set of the potential solutions:

Step 3. The following function is selected as the fitness function:

Step 4. Update the local optimal position $P_{ij}$ for each particle and other relevant variables.

Step 5. Update the global optimal position $P_{gj}$ for each particle and other relevant variables.

Step 6. Calculate the $M_{best}$ value and the random point $P_i$ for each particle.

Step 7. Update the position according to the probability plus and minus for each particle.

Step 8. If the end condition is met, the operation is end and the current best solution is obtained. Otherwise, $t=t+1$ is executed, return to Step 3 to recalculate until the termination is melted.

Step 9. The optimal parameter combination is entered in the SVM model in order to obtain the information fusion (CQPSM) method.

5.1. Fault diagnosis method

In order to effectively realize the fault diagnosis and obtain high correctness and speed, the proposed CQPSM method is introduced into fault diagnosis to propose a novel fault diagnosis (CQPSMFD) method in this paper. The process of the proposed CQPSMFD method is illustrated in Fig. 2.

Fig. 2The process of the proposed CQPSMFD method

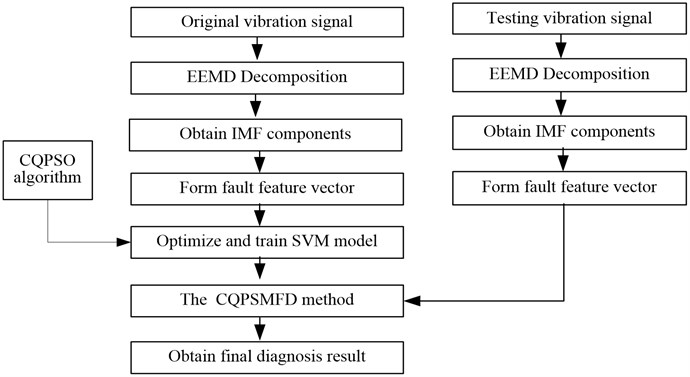
5.2. Experiment and result analysis

The standard vibration data from Case Western bearing dataset and the actual data of motor in industrial production are used to validate the effectiveness of the proposed CQPSMFD method. The experiment environments are Matlab2010b. The initial values of parameters for the CQPSMFD method could be a complicated problem itself, the change of parameters could affect the optimum value. The selected ones are those that gave the best computational results concerning both the quality of the solution and the run time needed to achieve this solution. The initial values are: population size $M=$60, learning factor $c_1=c_2=$2.0, control parameter ${\beta }_0=$1. The max iteration $T_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 500.

5.2.1. The standard vibration data for fault diagnosis

The 6205-2RS JEM SKF deep groove ball bearing is employed. In this bearing, the external diameter is 52 mm, the internal diameter is 25 mm, and thickness is 15 mm. These data are acquired with the 12 kHz sampling frequency. The vibration signals are 40 samples for the inner race fault, the outer race fault, rolling element fault and normal state respectively. Firstly, the vibration signals are decomposed by ensemble empirical mode decomposition (EEMD) respectively. The instantaneous amplitude energies of eight IMFs are extracted as the input of the CQPSMFD method. The obtained feature vectors are randomly divided into 30 training samples and 10 testing samples. The feature vectors of bearing are shown in Table 1.

The BPNFD method based on BP neural network, SVMFD based on SVM, POSMFD method based on PSO and SVM, QPOSMFD method based on QPSO and SVM are selected to compare with the CQPSMFD method. The comparison results are shown in Table 2.

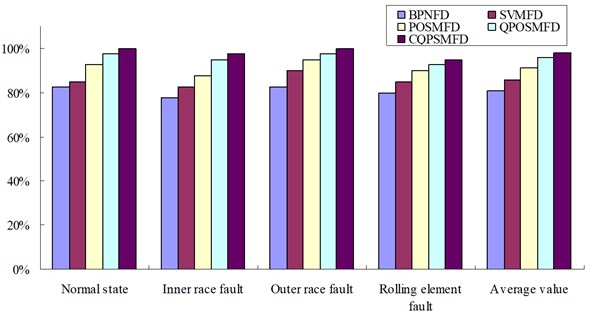
As can be seen from Table 2 and Fig. 3, the correctness rates of the proposed CQPSMFD method are 100.0 %, 97.5 %, 100.0 % and 95.0 % for normal state, inner race fault, outer race fault and rolling element fault respectively. For each standard vibration data, the average correctness rate of the proposed CQPSMFD method is 98.125 %. It is best diagnosis result than the BPNFD method, SVMFD method, POSMFD method and QPOSMFD method. The proposed CQPSMFD method can obtain the complete correctness result for the normal signal and outer race fault signal, the correctness rate is 100 %. So the comparison results show that the proposed CQPSMFD method takes on the higher fault pattern recognition accuracy for the standard vibration data in the experiment.

Table 1The feature vectors of bearing

State	Samples	The instantaneous amplitude energy of IMFs
		$E_1$	$E_2$	$E_3$	$E_4$	$E_5$	$E_6$	$E_7$	$E_8$
Normal state	1	0.512	0.705	0.104	0.251	0.388	0.072	0.007	0.003
	2	0.529	0.718	0.186	0.263	0.324	0.051	0.013	0.010
	3	0.536	0.726	0.241	0.278	0.285	0.043	0.024	0.013
Inner race fault	1	0.962	0.250	0.101	0.048	0.018	0.007	0.001	0.000
	2	0.951	0.292	0.103	0.053	0.017	0.004	0.003	0.001
	3	0.940	0.310	0.106	0.058	0.015	0.002	0.002	0.001
Outer race fault	1	0.741	0.668	0.108	0.029	0.010	0.001	0.001	0.000
	2	0.709	0.703	0.105	0.024	0.007	0.003	0.000	0.000
	3	0.688	0.726	0.102	0.020	0.003	0.004	0.003	0.002
Rolling element fault	1	0.725	0.633	0.240	0.157	0.035	0.006	0.004	0.003
	2	0.750	0.587	0.266	0.119	0.026	0.003	0.002	0.001
	3	0.778	0.553	0.289	0.098	0.024	0.002	0.001	0.000

Table 2The comparison of fault diagnosis results

State	Diagnosis correctness rate (%)
	BPNFD	SVMFD	POSMFD	QPOSMFD	CQPSMFD
Normal state	82.5 %	85.0 %	92.5 %	97.5 %	100.0 %
Inner race fault	77.5 %	82.5 %	87.5 %	95.0 %	97.5 %
Outer race fault	82.5 %	90.0 %	95.0 %	97.5 %	100.0 %
Rolling element fault	80.0 %	85.0 %	90.0 %	92.5 %	95.0 %
Average value	80.625 %	85.625 %	91.25 %	95.625 %	98.125 %

Fig. 3The correct rate comparison result for standard vibration data

5.2.2. The actual data of motor for fault diagnosis

The mechanical fault of motor rotor in industrial production is selected as the actual research object. The type of motor is Y132M-4 and rated speed is 1450 r/min in this paper. The actual vibration signals on the horizontal and vertical directions are collected by using eddy-current sensor. The main faults of motor rotor include the rotor unbalance, rotor misalignment, oil whirl, rotation detachment, surge, losing bearing house and so on. Due to the limited page, the normal state, rotor unbalance and oil whirl are only considered. $d=$0 represents the normal state, $d=$1 represents the rotor unbalance state and $d=$2 represents oil whirl state.

The experiment steps of CQPSMFD method for actual motor are described as follows.

Step 1. Obtain the training and testing date.

In this paper, we select 300 samples. 250 samples are randomly selected as the training samples, the rest (50) is regarded as the testing samples. The describing of these samples is shown in Table 3.

Table 3The describing of these samples

Data type	$d=$0	$d=$1	$d=$2
Training samples	50	108	92
Testing samples	8	23	19
Total samples	58	131	111

Step 2. Data preprocessing.

Firstly, the mapminmax normalized function in Matlab2010 is used to process the data to the interval of [0, 1]. Rough set is a mathematical method that can be employed to deal with the data with the imprecision, incompletion, vagueness, and uncertainty. It can discover implicit knowledge and reveal potential rules by analyzing and dealing with all kinds of imprecise, incomplete, and disaccord information. So the rough set is used to realize the reduction in order to delete the redundancy attributes and obtain the minimum rule set with the greatest degree.

Step 3. Optimize the parameters of the SVM.

The CQPSO algorithm is used to optimize the $\mathrm{\sigma }$and $C$ of the SVM in order to obtain the best parameter combination. The optimal values are obtained: $C=$0.024, $\sigma =$0.994.

Step 4. Obtain the CQPSM method.

The obtained parameter values are entered in the SVM model, and the training samples are used to continuously train the SVM for obtaining the optimal SVM (CQPSM).

Step 5. Obtain the CQPSMFD method.

The CQPSM method is applied in fault diagnosis to propose a novel fault diagnosis (CQPSMFD) method.

Step 6. Output diagnosis result.

The testing samples are used to test the effectiveness of the CQPSMFD method. The diagnosis results are obtained in Table 4.

Table 4The diagnosis results of CQPSMFD method

Motor state	Testing data	Testing result	Diagnosis result	Correct rate
Normal state	8	8	$d=$0	100 %
Rotor unbalance	23	22	$d=$1	95.7 %
Oil whirl fault	19	18	$d=$2	94.7 %
Average value				96.8 %

As can be seen from Table 4, for 50 testing samples, the proposed CQPSMFD method can better diagnose the normal state, rotor unbalance and oil whirl fault of motor. For the normal state, the proposed CQPSMFD method can obtain 100 % correct rate. For the rotor unbalance fault and oil whirl fault, the proposed CQPSMFD method can obtain 95.7 % and 94.7 % correct rate, respectively. For the motor fault, the proposed CQPSMFD method can obtain 96.8 % mean correct rate in the testing samples. So the experiment results show that the proposed CQPSMFD method has the higher diagnosis accuracy.

In order to further verify the effectiveness of the proposed CQPSMFD method, the BPNFD method based on BP neural network, SVMFD method based on SVM model, POSMFD method on PSO algorithm and SVM and QPOSMFD method on QPSO and SVM are used to compare with the proposed CQPSMFD method. The initial values of parameters of these methods are obtained by using the experiment. The results of fault diagnosis are shown in Table 5.

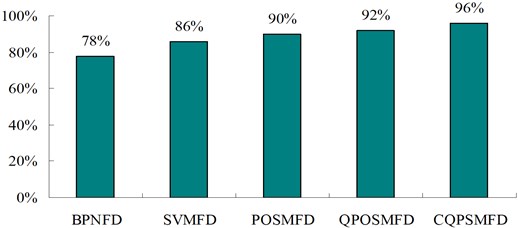
As can be seen from Table 5 and Fig. 4, for the given 50 testing samples, the fault diagnosis correct rate of the BPNFD method is lowest, its correct rate is only 78 %. The fault diagnosis correct rate of the SVMFD method is 86 %, and fault diagnosis correct rate of the POSMFD method is 90 %. The fault diagnosis correct rate of the QPOSMFD method is 92 %, and fault diagnosis correct rate of the CQPSMFD method is 96 %. Obviously, the proposed CQPSMFD method can obtain the best fault diagnosis correct rate than the BPNFD method, SVMFD method, POSMFD method and QPOSMFD method. So the experiment results show that the proposed CQPSMFD method can obtain the high fault diagnosis correct rate, and takes on strong robustness.

Table 5The comparison of diagnosis results

Diagnosis method	Testing samples	Testing result	Correct rate
BPNFD	50	39	78 %
SVMFD	50	43	86 %
POSMFD	50	45	90 %
QPOSMFD	50	46	92 %
CQPSMFD	50	48	96 %

Fig. 4The correct rate comparison of several methods