Abstract
The parameter-induced fractal erosion of the safe basin is investigated in a softening Duffing system. For a fixed excitation, we make the linear stiffness, the nonlinear stiffness and the damping coefficient as the control parameter. At first, the necessary condition for the fractal erosion of the safe basin is obtained by the Melnikov method. Then, the analytical predications are verified by the numerical simulations. With the variation of the stiffness or the damping coefficient, the fractal erosion of the safe basin will appear or vanish. Both the linear and the nonlinear stiffness influence the topology of the safe basin. With the increase of the linear stiffness, the fractal erosion of the safe basin will appear at first and then disappear gradually. The area of the safe basin is an increasing function of the linear stiffness. With the increase of the nonlinear stiffness, the fractal erosion of the safe basin appears and the area of the safe basin turns smaller. The topology of the safe basin is independent of the damping coefficient. For small damping coefficient, the fractal erosion of the safe basin occurs much more easily. The damping coefficient suppresses the fractal erosion of the safe basin.
1. Introduction
In engineering fields, great deals of interests have been devoted to the study of the engineering failures. For a safe structure, the response must be confined in a bounded space when the structure under a small perturbation. To this end, a definition named safe basin is originally proposed and explained by Thompson in the ship structure that under the lateral wave excitation at sea [1-3]. We give a big enough space region and let all initial conditions in this region. If the response of the structure cannot escape the region undergo a long time, the defined region is considered as a perfect safe basin. Instead, the region corresponds to the initial conditions is a corrosive safe basin. The erosion of the safe basin means the sensitive of the response to the initial condition. It is in accord with the chaos phenomenon. In other words, when the erosion of the safe basin occurs, the response of the structure is chaos. The Melnikov method is an effective tool to obtain the threshold for the chaos [4]. Therefore, the threshold for the erosion of the safe basin can also be obtained by the Melnikov integral. Usually, the corrosive safe basin has the fractal structure. Hence, the fractal erosion of the safe basin occurs when the perturbation exceeds the threshold. Freitas et al. studied the erosion of the safe basin for the transversal oscillations of a suspension bridge, and they found that the bridge will collapse if its deformation exceeds some threshold [5]. Gonçalves et al. investigated the global stability analysis of parametrically excited cylindrical shells through the evolution of basin boundaries [6]. Xu et al. used the time-dependent excitation to control the extent and the rate of the safe basin erosion [7]. The fractal erosion of the safe basin can also be effectively controlled by different kinds of time delayed feedback [8-11]. If the system is perturbed by random excitation, the stochastic Melnikov method should be applied to obtain the threshold for chaos [12-16]. Based on this mechanism, the fractal erosion of the safe basin is investigated when the structure is excited by different kinds of random perturbations [17-21]. General speaking, the random perturbation usually make the threshold turn small.
To our knowledge, most of the works about the fractal erosion of the safe basin are investigated in a structure that the system parameters are invariable. In other words, the damping coefficient and the stiffness coefficient are constants. The former researches are focused on the effect of the perturbation on the fractal erosion of the safe basin. In most case, the frequency of the perturbation suppresses the fractal erosion of the safe basin, while the amplitude of the perturbation enhances it. However, besides the perturbations, the system parameters are other important factors for the dynamical behaviors. A typical example is the parameter-induced stochastic resonance. One hand, for some stochastic systems, the random excitation can induce stochastic resonance when the noise amplitude is varied [22]. On the other hand, for the fixed noise case, the stochastic resonance can also be appearance when the system parameter is made as a control variable, and this phenomenon named parameter-induced stochastic resonance [23, 24]. In this paper, we would like to make clear a similar problem. Is there the parameter-induced fractal erosion of the safe basin existing in some structures? If so, what are the effects of different parameters on the fractal erosion of the safe basin? In view of this, we consider the problem in a softening Duffing oscillator. The softening oscillator is a typical differential equation that can describe many physical models. The outline of the paper is organized as follows. In Section 2, we give the mathematical model that will be studied. Then, we obtain the necessary condition for the fractal erosion of the safe basin. In Section 3, the analytical predications are verified by the numerical simulations. The effects of the linear stiffness, the nonlinear stiffness and the damping coefficient on the condition of the fractal erosion of the safe basin are investigated. Finally, a conclusion about the parameter-induced fractal erosion of the safe basin will be given in the last section.
2. Melnikov condition for fractal erosion of safe basin
We consider a kind of softening Duffing oscillator which subjected to a harmonica excitation, namely:
In Eq. (1), is a small positive parameter. Other positive parameters and are linear and nonlinear stiffness respectively. The coefficient is the damping parameter. and are the amplitude and frequency of the excitation signal.
In order to obtain the necessary condition for the appearance of a fractal basin boundary, the Melnikov method is applied. For the unperturbed case (i.e., 0), system Eq. (1) can be rewritten as:
The Hamilton of the unperturbed system is:
and there are one center (0, 0) and two saddle points . Since the Hamilton is conserved, any level curve constant is a solution of the Eq. (2). It is easy to obtain the system possesses a heteroclinic orbit to two saddle points , which is given by:
Using the method of residues, the Melnikov integral corresponds to system Eq. (1) is:
According to the dynamic theory, the stable and unstable manifolds will intersect transversely with each other when there are simple zeros in the Melnikov integral, which leads to the fractal erosion of the safe basin. Hence, the necessary condition for the fractal erosion of the safe basin is given by:
3. Parameter-induced fractal erosion of the safe basin
In this section, numerical simulations are conducted to verify the analytical prediction of the necessary condition for the fractal erosion of the safe basin. Throughout this paper, the initial condition lies in a big space region, i.e., –3:0.01:3, –3:0.01:3. The total time is long enough. In the following numerical calculations, we let 10000 and 0.1.
3.1. The linear stiffness induced fractal erosion of the safe basin
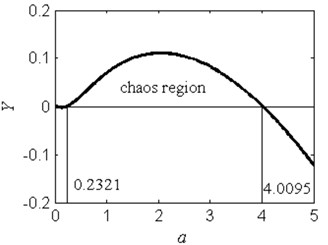
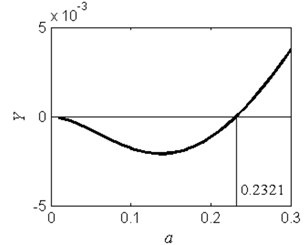
Letting , according to the condition in Eq. (6), the response is chaos when 0. The safe basin presents fractal erosion for this case. In Fig. 1, the chaos region is given on the - plane. In this figure, 0.23214.0095 is the chaos region, and the fractal erosion of the safe basin will appear when the parameter lies in this region. For all other values of , the safe basin will be a whole one without erosion. The critical values 0.2321 and 4.0095 are two bifurcation points for the fractal erosion of the safe basin. With the increase of the linear stiffness the evolution of the safe basin will be shown in the “no erosion → erosion → no erosion” form.
Fig. 1a) The chaos region in the a-Y plane, b) is the enlargement plot of a) for 0 <a< 0.3. The calculated parameters are ω= 1.2, f= 2.5, b= 1 and c= 1
a)
b)
In order to verify the validity of the analytical predication, the fractal erosion of the safe basin of system Eq. (1) under increasing the parameter is given in Fig. 2. The black points are the safe initial conditions. When 0.1, as is shown in Fig. 2(a), the safe basin is a complete attraction basin although its area is very small. There is no erosion in the safe basin for this case. It is according with the conclusion in Fig. 1(b). In Fig. 2(b)-2(k), when changes from 0.3 to 4, the evolution of the safe basin presents fractal erosion. In Fig. 2(l), for the case 5, the erosion of the safe basin vanishes. Another important result is the area of the safe basin depends on the parameter closely. With the increase of the parameter , the area of the safe basin turns larger gradually. Through simulation of the safe basin, the analytical predication for the fractal erosion of the safe basin is verified.
Fig. 2Fractal erosion of the safe basin of system Eq. (1) under increasing the parameter a when ω= 1.2, f= 2.5, b= 1 and c= 1
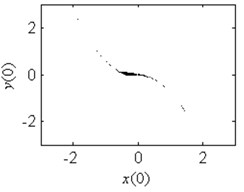
a) 0.1
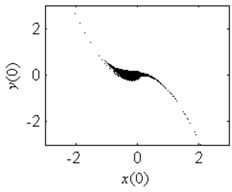
b) 0.3
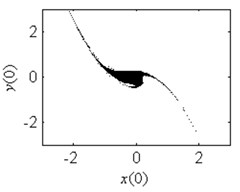
c) 0.5
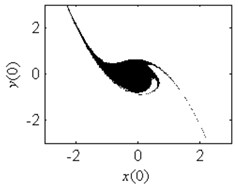
d) 1
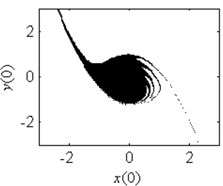
e) 1.5
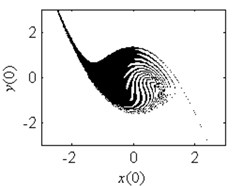
f) 2
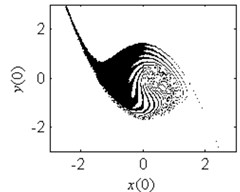
g) 2.1
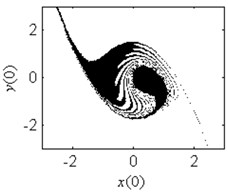
h) 2.2
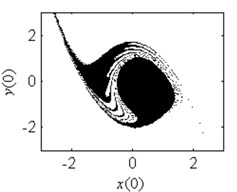
i) 2.5
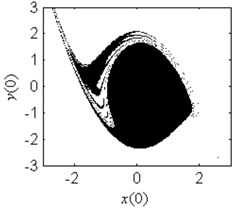
j) 3
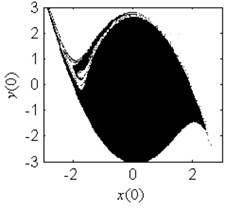
k) 4
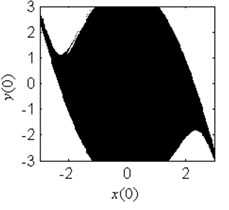
l) 5
3.2. The nonlinear stiffness induced fractal erosion of the safe basin
The chaos region versus the nonlinear stiffness is given in Fig. 3. With the increase of the parameter , the chaos region appears. The bifurcation point for the fractal erosion of the safe basin is 0.4143. When 0.4143, the safe basin present fractal boundary.
Fig. 3The chaos region in the Y-b plane for ω= 1.2, f= 2.5, a= 2 and c= 1
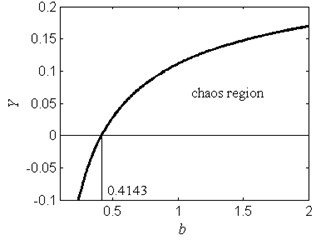
Fig. 4Fractal erosion of the safe basin of system Eq. (1) under increasing the parameter b when ω= 1.2, f= 2.5, a= 2 and c= 1
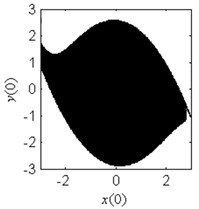
a) 0.3
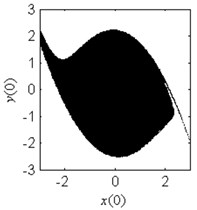
b) 0.4
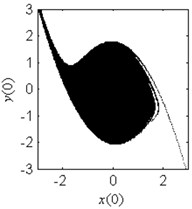
c) 0.6
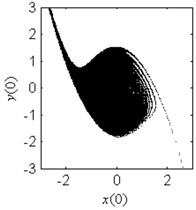
d) 0.8
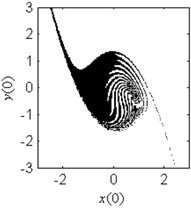
e) 1
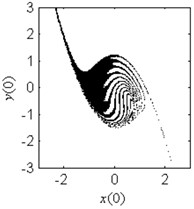
f) 1.2
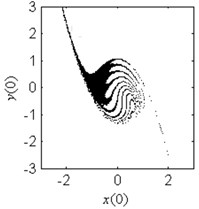
g) 1.5
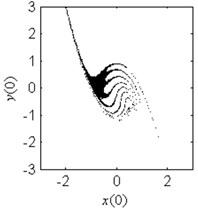
h) 2
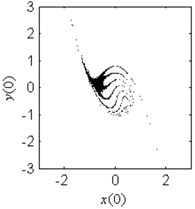
i) 2.5
In Fig. 4, the fractal erosion of the safe basin induced by the parameter is clearly shown. In Fig. 4(a) and 4(b), there is no fractal erosion in the boundary of the safe basin. It is accord with the safe region in Fig. 3. In Fig. 4(c)-4(i), with the increase of the parameter , the degree of the fractal erosion of the safe basin increase too. Another important fact is that the safe basin turns smaller and smaller with the increase of the parameter . Hence, the effect of the nonlinear stiffness on the safe basin is contrary to the effect of the linear stiffness on the safe basin.
3.3. The damping coefficient induced fractal erosion of the safe basin
In this subsection, we investigate the fractal erosion of the safe basin that induced by the damping coefficient. In Fig. 5, the chaos region in the - plane is given. The bifurcation point for the fractal boundary is 1.5537. When 1.5537, the safe basin presents fractal erosion. Otherwise, the safe basin is in a whole form. The variable is a linear function of the damping coefficient . This fact can also be obtained from Eq. (6). However, in Fig. 1 and Fig. 3, is a nonlinear function of the variable and .
Fig. 5The chaos region in the Y-c plane for ω= 1.2, f= 2.5, a= 2 and b= 1
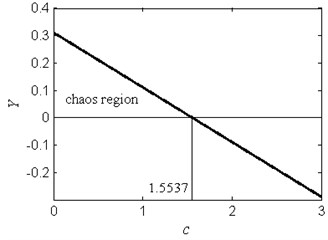
Fig. 6Fractal erosion of the safe basin of system Eq. (1) under increasing the parameter c when ω= 1.2, f= 2.5, a= 2 and b= 1
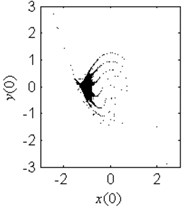
a) 0.1
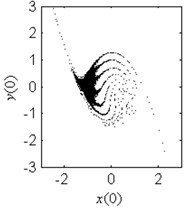
b) 0.3
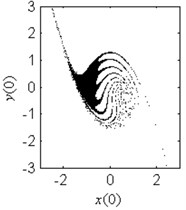
c) 0.5
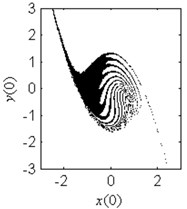
d) 0.8
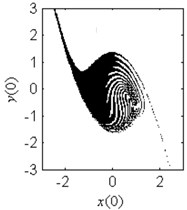
e) 1
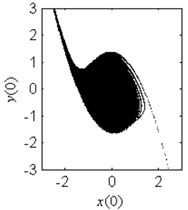
f) 1.2
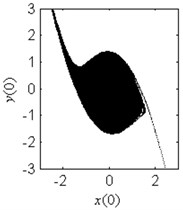
g) 1.5
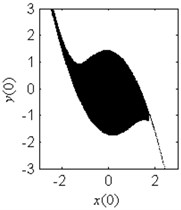
h) 1.8
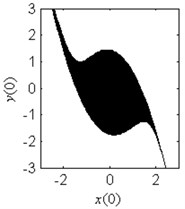
i) 2
In Fig. 6, the effect of the damping coefficient on the evolution of the safe basin is shown. In Fig. 6(a)-6(g), the safe basin presents fractal boundary. The value of the coefficient in these subplots corresponds to the chaos region in Fig. 5. Also in these subplots, with the increase of the damping parameter, the degree of the fractal erosion of the safe basin turns slighter, and the boundary of the safe basin turns smoother and smoother. In Fig. 6(h) and 6(i), there is no erosion in the safe basin. For these two cases, the coefficient lies in the safe region in Fig. 5. Another important fact is that the topology of the safe basin is independent of the coefficient . It is very different from the effects of the parameter and on the topology of the safe basin.
4. Conclusion
In the present paper, the fractal erosion of the safe basin in a typical softening Duffing oscillator is investigated. Different from the former literatures, we focus on the fractal erosion of the safe basin induced by the parameter, i.e., the linear stiffness, the nonlinear stiffness and the damping coefficient. At first, based on the Melnikov approach, we obtain the necessary condition for the fractal erosion of the safe basin. Then, some numerical simulations of the safe basin are conducted to verify the analytical predications. The numerical results are in good agreement with the analytical predications. For the parameter-induced fractal erosion of the safe basin, the effects of the linear stiffness, the nonlinear stiffness, and the damping coefficient on the safe basin are very different. With the increase of the linear stiffness, the fractal erosion of the safe basin will appear at first and then vanish gradually. The area of the safe basin turns larger with the increase of the linear stiffness. With the increase of the nonlinear stiffness, the degree of the fractal erosion of the safe basin increase and the area of the safe basin turns small. The damping coefficient is independent of the topology of the safe basin, but it suppresses the fractal erosion of the safe basin.
Instead of the excitation induced fractal erosion in the safe basin, we give a new factor that can also induce the fractal erosion in the safe basin, i.e., the parameter-induced fractal erosion in the safe basin. The results in this paper contribute to a better understanding of the fractal erosion of the safe basin in the engineering structure. Moreover, the results are significance in the engineering applications, especially in the field of the vibration engineering. On the one hand, in the analysis of a nonlinear vibration system, the system parameters must be considered in the viewpoint of avoiding the dangerous induced by the fractal erosion of the safe basin. On the other hand, for designing a nonlinear vibration system, if we choose traditional methods, we may only consider the response amplitude under the harmonica excitation in the periodic or quasi-periodic viewpoint and ignore the fractal erosion of the safe basin. Even though the response of the system is stable in the traditional viewpoint, it may be unstable due to the existence of the fractal erosion of the safe basin. In the system design process, we need to consider to preventing the fractal erosion of the safe basin and enhancing the stability of the system by adjusting the system parameters according to the results in this paper. Then, the probability of the safety of the system is improved. Apparently, the rules of the parameters on the fractal erosion of the safe basin have reference value on the design of a nonlinear vibration system.
References
-
Thompson J. M. T., Soliman M. S. Fractal control boundaries of driven oscillators and their relevance to safe engineering design. Proceedings of the Royal Society a Mathematical Physical and Engineering Sciences, Vol. 319, Issue 428, 1991, p. 1-13.
-
Thompson J. M. T., Rainey R. C. T., Soliman M. S. Ship stability criteria based on chaotic transients from incursive fractals. Philosophical Transactions of the Royal Society B Biological Sciences, Vol. 332, Issue 1624, 1990, p. 149-167.
-
Soliman M. S., Thompson J. M. Global dynamics underlying sharp basin erosion in nonlinear driven oscillators. Physical Review A, Vol. 45, Issue 6, 1992, p. 3425-3431.
-
Hu H. Y. Applied Nonlinear Dynamics. Aviation Industry Press, Beijing, 2000.
-
De Freitas M. S. T., Viana R. L., Grebogi C. Erosion of the safe basin for the transversal oscillations of a suspension bridge. Chaos Solitons and Fractals, Vol. 18, Issue 4, 2003, p. 829-841.
-
Gonçalves P. B., Silva F. M. A., Prado Z. J. G. N. Global stability analysis of parametrically excited cylindrical shells through the evolution of basin boundaries. Nonlinear Dynamics, Vol. 50, Issue 1, 2007, p. 121-145.
-
Xu J., Lu Q. Z., Huang K. L. Controlling erosion of safe basin in nonlinear parametrically excited systems. Acta Mechanica Sinica, Vol. 12, Issue 3, 1996, p. 281-288.
-
Shang H., Xu J. Delayed feedbacks to control the fractal erosion of safe basins in a parametrically excited system. Chaos Solitons and Fractals, Vol. 41, Issue 4, 2009, p. 1880-1896.
-
Naik R. D., Singru P. M. Resonance, stability and chaotic vibration of a quarter-car vehicle model with time-delay feedback. Communications in Nonlinear Science and Numerical Simulation, Vol. 15, Issue 8, 2011, p. 3397-3410.
-
Alsaleem F. M., Younis M. I. Stabilization of electrostatic MEMS resonators using a delayed feedback controller. Smart Materials and Structures, Vol. 19, Issue 19, 2010, p. 335-341.
-
Shang H. L., Wen Y. P. Fractal erosion of the safe basin in a helmholtz oscillator and its control by linear delayed velocity feedback. Chinese Physics Letters, Vol. 28, Issue 11, 2011, p. 110503-110503.
-
Simiu E., Frey M. R. Melnikov processes and noise-induced exits from a well. Journal of Engineering Mechanics, Vol. 122, Issue 3, 1996, p. 263-270.
-
Lin H., Yim S. C. S. Chaotic roll motion and capsize of ships under periodic excitation with random noise. Applied Ocean Research, Vol. 17, Issue 3, 1995, p. 185-204.
-
Bulsara A. R., Schieve W. C., Jacobs E. W. Homoclinic chaos in systems perturbed by weak Langevin noise. Physical Review A, Vol. 41, Issue 41, 1990, p. 668-681.
-
Lin H., Yim S. C. S. Analysis of a nonlinear system exhibiting chaotic, noisy chaotic, and random behaviors. Journal of Applied Mechanics, Vol. 63, Issue 2, 1996, p. 509-516.
-
Liu W. Y., Zhu W. Q., Huang Z. L. Effect of bounded noise on chaotic motion of duffing oscillator under parametric excitation. Chaos Solitons and Fractals, Vol. 12, Issue 3, 2011, p. 527-537.
-
Gan C. Noise-induced chaos and basin erosion in softening Duffing oscillator. Chaos Solitons and Fractals, Vol. 25, Issue 5, 2005, p. 1069-1081.
-
Gan C. Noise-induced chaos in duffing oscillator with double wells. Nonlinear Dynamics, Vol. 45, Issue 3, 2006, p. 305-317.
-
Li X. C, Xu W., Li R. H. Chaotic motion of the dynamical system under both additive and multiplicative noise excitations. Chinese Physics B, Vol. 17, Issue 2, 2008, p. 557-568.
-
Wei D. Q., Zhang B., Qiu D. Y., Luo X. S. Effect of noise on erosion of safe basin in power system. Nonlinear Dynamics, Vol. 61, Issue 3, 2010, p. 477-482.
-
Li S., Li Q., Li J., Feng J. Chaos prediction and control of good win’s nonlinear accelerator model. Nonlinear Analysis Real World Applications, Vol. 12, Issue 4, 2011, p. 1950-1960.
-
Gammaitoni L., Hänggi P., Jung P., Marchesoni F. Stochastic resonance. Reviews of Modern Physics, Vol. 70, Issue 1, 1998, p. 223-287.
-
Duan F. B., Xu B. H. Parameter-induced stochastic resonance and baseband binary pam signals transmission over an awgn channel. International Journal of Bifurcation and Chaos, Vol. 13, Issue 2, 2011, p. 411-425.
-
Jiang S., Guo F., Zhou Y., Gu T. Parameter-induced stochastic resonance in an over-damped linear system. Physica A Statistical Mechanics and Its Applications, Vol. 375, Issue 2, 2007, p. 483-491.
Cited by
About this article
This research was supported by the National Science and Technology Support Program (No. 2014BAB01B01), Jiangsu Industry-Academia-Research Prospective Joint Study Program (No. BY2015023-08), Top-notch Academic Programs Project of Jiangsu Higher Education Institutions and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
