Abstract
Through analysis of the time-delay characteristics of stabilized and tracking platform position tracking loop and of attitude disturbance exciting in stabilization and tracking platform systems, a compound control method based on adaptive fuzzy-grey prediction control (CAGPC) is proposed to improve the disturbance suppression performance and system response of stabilized and tracking platform system. Firstly, the feedforward controller which is to improve disturbance suppression performance of stabilized and tracking platform servo system and aiming at the external disturbances is introduced. Secondly, aiming at the disadvantages of conventional fixed step size of Fuzzy-grey prediction and the prediction error forecast model has, an adaptive adjustment module adjusting the prediction step and comprehensive error weight at the same time is proposed, according to the actual control system error and the prediction error, the Fuzzy-grey prediction step and the prediction error weights are regulated while to improve the control precision and the adaptability of the system prediction model; At last, Numerical simulation results and the stabilized and tracking platform experimental verification illustrate that the compound control method can improve the stable platform servo system response and the ability of suppress external disturbances and the CAGPC control method has better performance in the stabilized and tracking platform system.
1. Introduction
The stabilized and tracking platform is the device which can keep the stabilized objects in a stable attitude under the actions of external disturbances and make the tracking systems work following the given orders by people in inertial spaces. The stabilizaed and tracking platform used in moving base systems are usually affected by the carrier attitude in the working process, especially when used in the shipborne systems and vehicle-mounted systems. As is known to all, in the control process, external disturbance is usually measured but uncontrollable, as long as the external disturbance process characteristics is understood and disturbance is measured accurately, the feedforward control can compensate the disturbance based on the disturbance, which can just eliminate the disturbance effect and keep the control volume is constant, so feedforward control is also known as “disturbance compensator”. The feedforward controller can be processed in time after the disturbance, and it is effective to suppress the dynamic and static deviation caused by the disturbance. In addition, the feedforward control is an open-loop control, so as long as the system is stable, the control system must be stable. Many studies validate that feedforward control can improve system robustness and the external disturbance isolation degree effectively. In [1], Erdal and Okyay took a non-linear liquid level system as a test bed to examine the grey fuzzy PID controller, and the results indicate that grey predictive controller has the ability to control the non-linear system accurately with little overshoot, with no steady-state error. In [2], In order to solve the current tracking control problem in electric power steering (EPS), the system mathematical model was established and the system type was analyzed, disadvantages of the conventional PID control and fuzzy PID control were studied. Using the feed-forward and feedback integrating control theory, a feed-forward control integrated with fuzzy PID feedback control algorithm was proposed. Experiment comparisons showed that the proposed algorithm could significantly improve the system stability, response rapidity and following accuracy in current control of electric power steering system. In [3], In order to reduce beam jitter introduced by all kinds of broadband and narrowband disturbance, and improve the satellite acquisition, pointing and tracking (ATP) systemcs pointing accuracy, a new kind of composite control was constructed based on the traditional proportiona-integra-differential (PID) feedback algorithm and the new adaptive feedforward algorithm. Experimental results indicated that the error adaptive feedforward composite control algorithmcs accuracy was nearly 5 times better than that of the classical PID control algorithm and1time better than that of the adaptive feedforward algorithm. In [4-8], feedforward control methods are used to control the stability of the inertial stabilized platform tracking, carrier based optoelectronic devices, photovoltaic grid connected, servo system high speed positioning and pH control in food industry. In [9], the disturbance based on feedforward control in seeker stability platform to eliminate disturbed angular velocity form platform base. In [10], a control scheme combining the dynamics disturbance force forward feed to solve the strong disturbance force form the dynamics coupling existing in the hydraulic Stewart platform. Of course, it is not easy to achieve full compensation, while the disturbance is often more than one or more specific. In order to ensure a greater adaptability, in many situations, the feedforward control and feedback control are usually combined to form a feedforward- feedback control system, which can obtain excellent control quality even if the system is under large and frequent disturbance.
Time lag would appear in the operating process of the adjusting mechanism because that the loads the inertia of the stabilized and tracking platform is huge. In addition, calculation of control variables and unsuitable sampling frequency can bring certain time delays [11]. As we know, the big overshot and control quality can be produced and decreased by the time delay. Grey predictive controller could be employed to improve control quality of time delay system [12]. Grey System Theory, pioneered by Deng (1982), is a new method for studying uncertain problems with less data and poor information, and is applicable to system analysis, data processing, modeling, prediction, decision making and control [13]. GM(1,1) model is the most frequently used model in grey predictions which is suitable for the observed data with exponential distributing, and it has been widely and successfully applied to various systems such as financial, economic, scientific, technological, industrial, social, etc. systems [11-22]. In [23-25], PID based grey predictive controllers were used to control the sliding inverted pendulum, dynamic tension during cold rolling, vegetable grasping system, respectively. As is known to all, all of prediction models have the predictive errors more or less. In [26, 27], a novel self-adjustable grey prediction controller was proposed respectively. In the proposed control scheme, the current output error and the predicted output error were combined together to form an integrated error. Simulation results indicated that the controller can achieve better dynamic performance and robustness than traditional feedback control. Therefore, in this paper, fuzzy-grey predictive controller will be applied in the stabilized and tracking platform system to compensate the time delay.
Therefore, in this study, a compound control method based on adaptive fuzzy-grey prediction control and feedforward control (CAGPC) is proposed to improve the system response and disturbance suppression performance of stabilized and tracking platform system. In Section 2, the system composition, the control structure of the tracking stable platform, and the influence of the external disturbance and time lag in the servo control system is introduced respectively. Section 3 introduces the design of the newly proposed controller in detail, including the designs of feedforward controller and adaptive fuzzy-grey controller, and the adaptive adjustment error model is also designed. Then in Section 4, some numerical simulations are carried out to demonstrate the effectiveness of the novel control strategy. Finally, concluding remarks are presented in Section 5.
2. The servo control structure of stabilized and tracking platform system
The stabilized and tracking platform system consists of two layers of control mechanism. The bottom layer is the base stable layer, and the upper layer is the target tracking layer. The system includes industrial control computer, attitude measurement system, servo motor, servo driver, DSP controller, parallel regulation mechanism, pitch and azimuth tracking control mechanism, photoelectric tracking system, etc. The attitude information of stabilized and tracking platform system is measured by attitude measurement system for real-time detection, and the two axes in the stable layer adjusting mechanism is driven to adjust the attitude of the platform and complete the control of the system platform of the close loop stability. The tracking layer receive the information sent by industrial control computer or photoelectric tracking system and the optoelectronic devices is under the control mechanism of azimuth and elevation for the target real-time tracking precision, so the dual function of stabilization and tracking is completed at the same time. The stabilized and tracking system is as follows:
Fig. 1The stabilized and tracking platform system
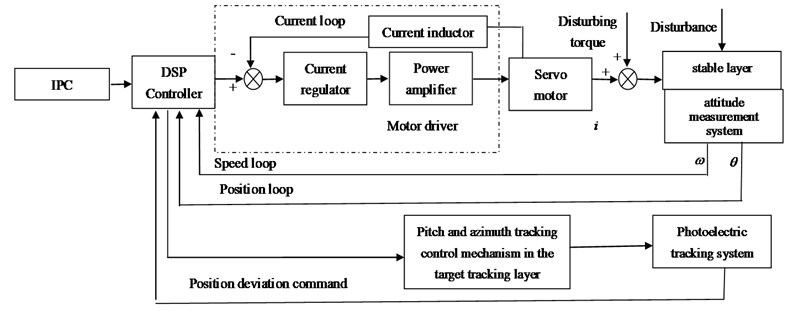
Fig. 2Position loop of stabilization and tracking platform
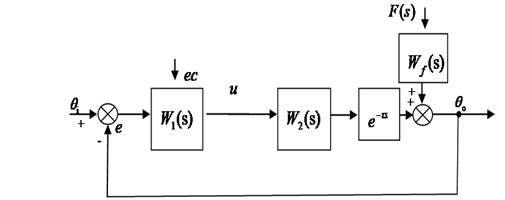
In Fig. 2, , , , , are reference input, system output, tracking error, changes of tracking error, feedback control signal respectively. , and are the controller, the transfer function of control object and the delay link respectively. is the transfer function of disturbance (Relations between platform and carrier is a mechanical solid connection so the disturbance channel can be regarded as pure rigid connection, And here is taken to be proportional component). Considering the influence of time delay in position loop and with appropriate simplifications, the transfer function of control object in position loop for the stabilized and tracking platform is:
where , is voltage constant, is mechanical time constant, is half of winding resistance , is the approximate proportional factor between platform rotational angular rate and motor speed, is amplification of current feedback.
In the stabilized and tracking system, the servo control of the stable layer is very important, because the stable layer provides a stable level base for the tracking layer. From the above comprehensive analysis, we can know that the stability of servo control is affected by external disturbance and time lag, so this paper mainly focuses on the design of disturbance rejection controller and the processing of time delay. Therefore, according to the existing external uncontrollable disturbances and time-delay, the feedforward controller and the adaptive fuzzy-grey prediction controller are designed. And the forecast model of the fuzzy-grey model is optimized and the error adaptive compensation is made respectively. The specific process is detailed in the 3 section.
3. Compound control strategy based on adaptive Fuzzy-grey predictive controller
3.1. The design of disturbance feedforward controller
Without considering the time delay, the external disturbance of the stabilized and tracking platform mainly comes from the disturbance of the carrier’s attitude, so the control structure of the position loop of the stabilized and tracking platform can be simplified as follows.
Fig. 3Disturbance feedforward control structure
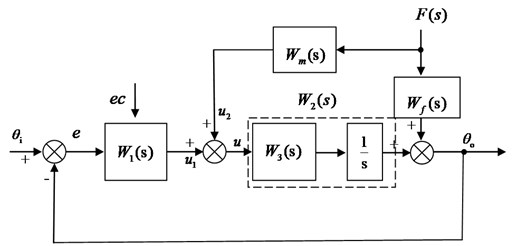
In Fig. 3, and are transfer functions of feedforward controller and disturbance channel respectively. From Fig. 3, we can obtain:
The transfer function form attitude disturbance to system output is:
When there is only exists attitude disturbance , according to the absolute invariance principle (, ), the Eq. (4) should be met as below:
Hence the following equation can be obtained:
Because the platform and the carrier are fixedly connected with the machine, and the interference channel can be viewed as a pure rigid links, so the interference channel transfer function can be viewed as a proportion links. And closed loop transfer function of the speed loop which is simplified is an order link, so the molecular order of will be higher than the denominator order. In the implementation of the system, we need to introduce a number of higher order derivatives of the input signal as the feed forward control signal [28]. When using the static feedforward, for convenience, take to make the system output to the input without static error, and we can obtain from Fig. 3:
What’s more, the equation can be transformed into:
where is feedback control signal, is the feedforward coefficient, and is the sampling period. The feedforward coefficient has been introduced in detail in the paper [29], and here is no longer repeat again.
3.2. Adaptive Fuzzy-grey predictive controller
In Fig. 4, Step switching module is the mechanism to determine prediction step size, Modified GM(1.1) module is the grey predictive module, and are the weight of the prediction error and the actual error in the comprehensive error respectively. is the transfer functions of feedforward controller and is the disturbance channel respectively.
Fig. 4Compound control structure based on adaptive Fuzzy-grey prediction control
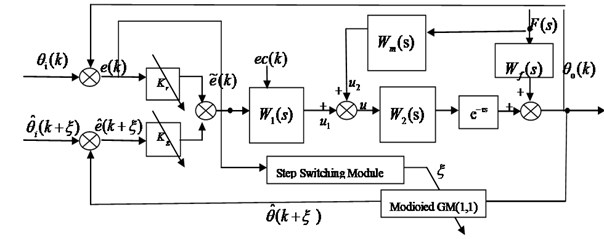
In Fig. 4, Modified GM(1,1) module is the grey prediction module, Let stand for a sample of the output components with which is the output at time . So, we can obtain a positive sequence by translational processing. Then GM(1,1) model could be constructed with the positive sequence , A preliminary transformation called accumulated generating operation (AGO) should be applied to reduce the noise of series efficiently and to get a new monotonically increasing data series at the same time:
By and , the grey differential equation can be formed as follows:
where is developing coefficient and is the grey input. Mean generation of consecutive neighbors is suitable for gentle sequences with small intervals. However, the sequence data changes greatly, mean generation may cause big lag errors. Therefore, a new optimal background value formula is used to generate the mean sequence in [30] to solve this problem, and its effectiveness is validated with examples. Here we will employ Eq. (11) to generate the mean sequence for GM(1,1) as well:
Adopt least square method to estimate the model parameters :
where , are the data matrix and data vector respectively:
White-formed ordinary differential equation of grey model GM(1,1) is:
Solve Eq. (13) with the obtained model parameters and apply the inverse AGO (IAGO) to figure out predicted values, the specific calculation process has been described in the paper [31]:
where is prediction step. Since GM(1,1) model parameters are obtained with least square method, the fitting curve may not pass through the first point so that using in Eq. (14) as the initialization may be not reasonable. Based on the principle that the new information should be used fully, it is effective to endow more weigh for new information so that the th vector of the original sequence will be used as the initialization in GM(1,1) model. We can obtain:
At last, we can obtain the predicted values of modified GM(1,1) module:
Finally, we can obtain the predictive system output by inversing translational processing. In a grey predictive control system, predictions are often done using metabolic models. Thus, the parameters of the prediction device vary with time, and this would guarantee a strong adaptability of the system [22].
As we know, the prediction step size decides the predictive value and finally affects the control performance, so an adaptive step switching module is adopted to regulate the appropriate prediction step size of the grey predictor. When the prediction step fixed step size of the grey prediction controller is a negative or small positive number, the response time of the system is short; when the prediction step is a large and positive number, the response time of the system is long. The negative-step can increase the upward momentum of the output curve for shortening the settling time, and appropriate positive-steps can be used to prevent the overshooting. Thus, for obtaining an excellent system control performance, we use the following switching mechanism in CAGPC to determine prediction step size which would affect the generated control signal [22, 27]:
where and are the switching values, , , and are the big positive-step, middle positive-step, small positive-step and negative-step respectively for different error .
3.3. Adaptive adjustment error module
As is known to all, all of prediction models have the predictive errors more or less. In order to reduce the effect of predictive error to system, an adaptive adjustment error module is designed to do with the predictive errors. In Fig. 4, assumption and are the input of system at time and respectively, and are the output of system at time and the modified GM(1,1) module predictive value at time separately, and are the actual system error and predictive error of system at time and individually, is the comprehensive error. Thus, for obtaining an excellent system control performance, we use the following mechanism in system to determine the weight of prediction error in the comprehensive error [26, 27]:
Form Eqs. (20-22), we can see that the actual error and the prediction error are combined together to form an comprehensive error. Furthermore, this module can automatically adjust CAGPC parameters according to the precision of GM(1,1) in order to achieve better control performance and robustness.
4. Numerical simulations
For showing the efficiency of the proposed control strategy, take an actual stabilized and tracking platform system as an example to analyze. Parameters of the studied stabilized and tracking platform system is shown in Table 1.
Table 1Parameters of a stabilized and tracking platform system
(v) | (s) | (Ω) | (s) | ||
140 | 2.39×10-3 | 18.1 | 6 | 0.667 | 0.020 |
We use the MATLAB software to finish the simulations. Validation of Fuzzy-grey predictive controller is carried first. For the control object described by Eq. (1) and Table 1, there is 0.0016, and take and . Proportional controller (KnC), grey predictive controller (GPC) and the CAGPC are employed as regulators of position loop respectively. The fixed prediction step of GPC is 1. The adaptive steps of CAGPC are determined as following:
4.1. System responses of step signal
First, system responses of step signal are illustrated in Figs. 5-6 respectively.
Fig. 5τ=0.8Tr, Step response of the system
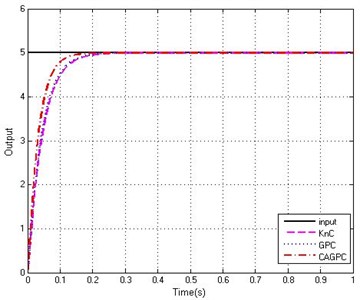
a) Response curves
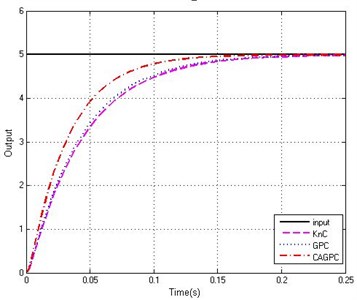
b) Partial enlarged curves
From the Fig. 5 and Fig. 6, we can see that, for the same control system, the delay time is different, but the control effect of the system is basically the same. Through comparison of GPC and KnC, we can find that the performance of GPC is better than KnC for increasing the response of the system, which indicates that grey prediction control is more applicable than the KnC in the control system. In the whole process, the performance of CAGPC is the best. Because the response ability of the system is greatly improved and system does not appear to be overshoot. Consequently, we reach a conclusion that CAGPC could effectively solve the problems of time delay in the stabilized and tracking platform system.
Fig. 6τ=0.2Tr, Step response of the system
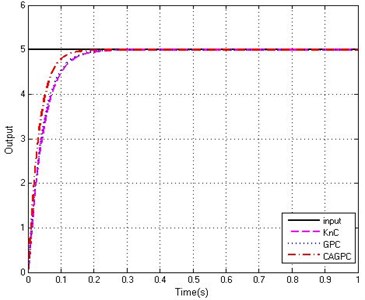
a) Response curves
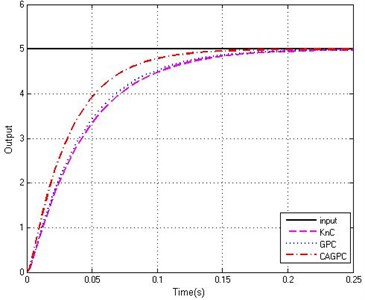
b) Partial enlarged curves
4.2. Tracking abilities of sinusoidal signal
Firstly, we employ the proportional controller (KnC), the fixed step grey controller without feedforward controller (GPC), Smith predictive controller (SPC) [31], fuzzy controller (FC) and the CAGPC as regulators of position loop respectively. Furthermore, it is assumed that the external disturbance is the interference of the uniform variation and we take as the disturbance. The transfer function of the interference channel is (which is the proportion link) and the proportional amplification factor is 10. The tracking results of sinusoidal signal are as follows:
The tracking curves of sine signal of which amplitude is 20° and the tracking error curves are shown in Figure 7. Under the same interference effect, five controllers all have good tracking abilities for tracking the sinusoidal signal and the tracking error is suppressed in the range of 1°. Among them, due to the presence of feedback time delay and interference effects, the performance of the proportion controller (KnC) and fuzzy controller (FC) is the worst and the maximum tracking error is 0.837°. In the whole process, the control performance of the FC is better than the KnC. While fixed step grey controller (GPC) and Smith predictive controller (SPC) can solve the lag problem in a certain extent and cannot inhibit the external interference without the feedforward controller, which leads to large tracking error. Throughout the whole control process, the performance of CAGPC is a little better than other four controllers and the maximum tracking error of CAGPC is only 0.312°, because not only the time delay is improved effectively but also the external disturbance has been suppressed obviously. Based on the results obtained, we can reach a conclusion that the CAGPC can suppress external disturbances and improve the response ability of system to decrease the influence of external disturbance and time delay in the stabilized and tracking platform system.
4.3. Tracking abilities of complex signal
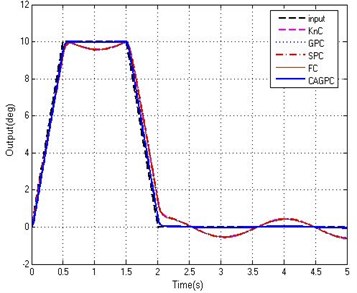
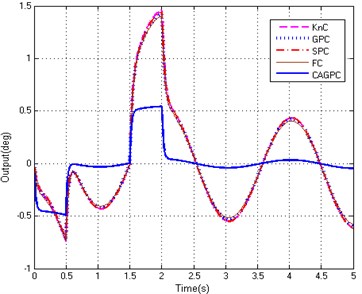
In order to further evaluate the performance of the method, with the same disturbance excitation as described in Section 4.2, when the input signal is a signal of drastic change (Namely the input signal changes in a short period of time). The process of signal change includes the acceleration of the increase - stable - deceleration process. We employ the proportional controller (KnC), the fixed step grey controller without feedforward controller (GPC), Smith predictive controller (SPC), fuzzy controller (FC) and the CAGPC as regulators of position loop respectively. And the proportional amplification factor is 10 too. The tracking abilities of five controllers are shown in Fig. 8.
Fig. 7Tracking abilities of five controllers
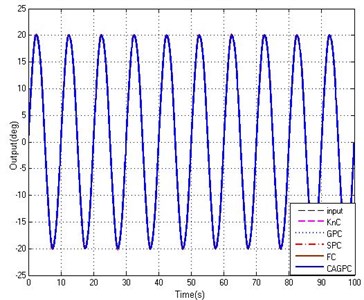
a) Tracking curves
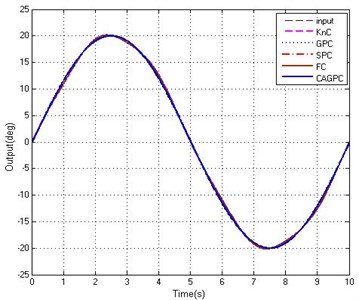
b) Partial enlarged curves
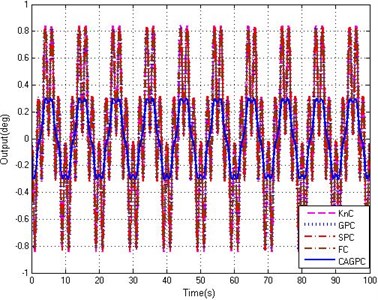
c) Tracking error curves
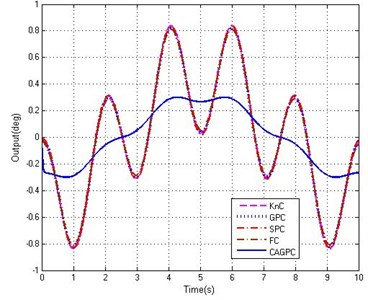
d) Partial enlarged curves
Fig. 8 illustrates five controllers all have certain tracking abilities for tracking the complex signal under the same interference effect. When the input signal changes dramatically, the tracking error of five controllers is a little larger in a certain extent. For the four controllers of the KnC, GPC, SPC and FC, when the signal from the acceleration to the stationary phase and from the smooth to the deceleration phase, at this point the tracking error is the maximum and the maximum tracking error is 1.48°. Among the five controllers, the maximum tracking error of the CAGPC is only 0.502° and he tracking error is suppressed in the range of 0.6°. Because the CAGPC has improved the time delay effectively, and also suppressed the external disturbance obviously. Compared with the other four controllers, the CAGPC control method has better performance in the stabilized and tracking platform system.
4.4. Abilities of suppressing the mutation interference
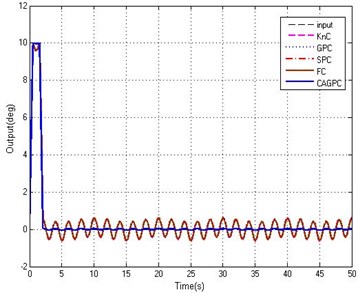
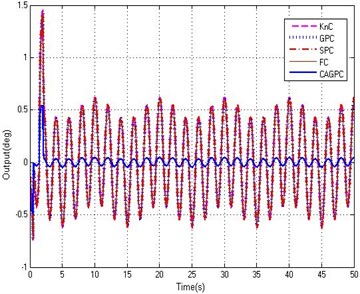
In order to further verify the validity and authenticity of the algorithm, the abrupt and harsh interference is employed to carry out the simulation test. For the external disturbance mutation interference, such as in the vehicle stabilized and tracking platform, the carrier is affected suddenly by the pavement heave, which causes the stabilized and tracking platform to tilt in a short time. This time we assume that the external unpredictable mutations interfere with the first rapidly increases to a peak, lasts for a short time and then decreases rapidly to zero value. As is shown in the Fig. 9, a trapezoidal signal with a peak value of 5 is used to simulate the external disturbance. We employ the proportional controller (KnC), the fixed step grey controller without feedforward controller (GPC), Smith predictive controller (SPC), fuzzy controller (FC) and the CAGPC as regulators of position loop respectively. The tracking abilities of five controllers are shown in Fig. 10.
Fig. 8Tracking abilities of five controllers
a) Tracking curves
b) Partial enlarged curves
c) Tracking curves
d) Partial enlarged curves
Fig. 9Simulation of disturbance
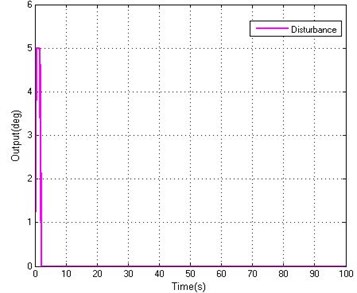
a) Curves of disturbance
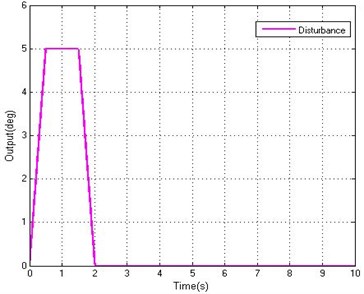
b) Partial enlarged curves
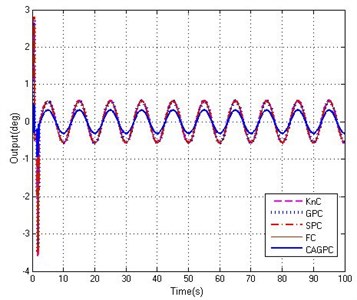
From Fig. 10, when the stabilized and tracking platform system is affected by the mutation interference, five controllers of KnC, GPC, SPC, FC and CAGPC have been influenced by different degrees and the control effect is not the same. For the KnC, GPC, SPC, and FC four controllers, in the disturbance of the mutation turning point, there is a big error, the largest of which is 2.87° and the minimum of which is almost 2.62°. The maximum tracking error of CAGPC is only 0.92°, and compared with the first four controllers, the CAGPC has obvious advantage than the first four controllers. Throughout the whole process of control, the CAGPC control method has better performance in the stabilized and tracking platform system under the abrupt and harsh interference, that indicates the CAGPC has a strong ability to suppress the abrupt and harsh interference.
Fig. 10Tracking abilities of five controllers
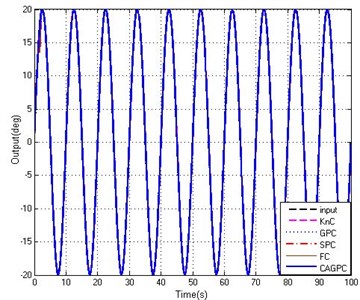
a) Tracking curves
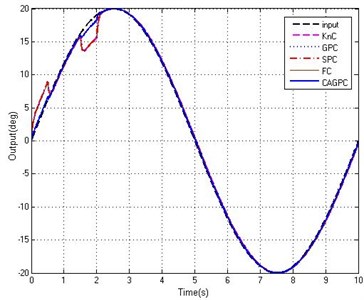
b) Partial enlarged curves
c) Tracking curves
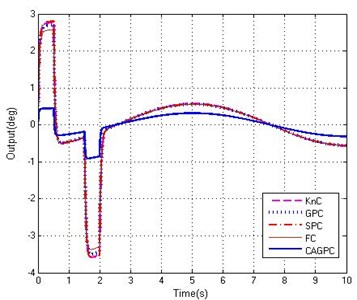
d) Partial enlarged curves
4.5. Turntable experiments
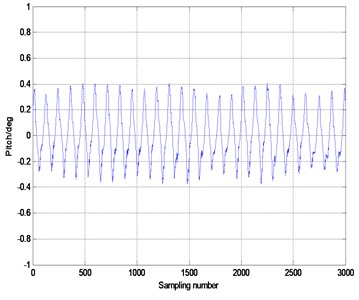
Turntable experiments are carried out in laboratory to examine the application performance of CAGPC ulteriorly. Stabilized and tracking platform is mounted on a turntable, and the turntable is rotated manually to simulate carrier motion. Stabilized and tracking platform load is 35 kg, the bottom stabilized platform diameter is 450 mm, the frequency of disturbance is about 1 Hz, the stable layer regulating shaft adjusting range is ±20°. The range of azimuth adjustment and pitch angle range of the upper tracking platform is 360°and ±5°respectively. The stabilizing performances of stabilizated and tracking platform ender disturbance excitations of 10° and 20° are shown in Figs. 9-10 respectively.
In Fig. 11, the stabilization precision of stabilized and tracking platform under disturbance excitation of 10° is in ±0.2° approximately, and the RMS error is only 0.165. In Fig. 12, the stabilization accuracy of stabilized and tracking platform under disturbance excitation of 20° is inferior. In addition, the stabilization precision of stabilized and tracking platform is in ±0.4° approximately except some glitches. Consequently, we can reach a conclusion with no doubt: the compound control method based on adaptive fuzzy-grey predictive control and feedforward control (CAGPC) is feasible for stabilized and tracking platform system.
Fig. 11Stabilized platform stabilization ability of interference amplitudes of 10 deg
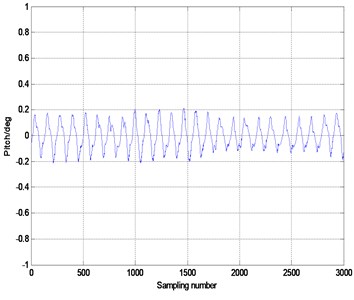
Fig. 12Stabilized platform stabilization ability of interference amplitudes of 20 deg
5. Conclusions
A compound control method based on adaptive fuzzy-grey predictive control and feedforward control (CAGPC) is proposed to improve the system response and disturbance suppression performance of stabilized and tracking platform system. Firstly, the feedforward compensation controller which is to improve disturbance suppression performance of stabilized platform servo system and aiming at the external disturbances is introduced. Secondly, aiming at the disadvantages of conventional fixed step size of grey prediction and the prediction error forecast model has, an adaptive adjustment module adjusting the prediction step and comprehensive error weight at the same time is proposed, according to the actual control system error and the prediction error, the grey prediction step and the prediction error weights are regulated while to improve the control precision and the adaptability of the system prediction model; At last, Numerical simulation results and the stabilized and tracking platform experimental verification illustrate that the compound control method based on adaptive fuzzy-grey prediction control can improve the stable platform servo system response and the ability of suppress external disturbances.
1) Simulations validate that feedforward control can suppress the external disturbance of stabilization and tracking platform system effectively.
2) AGPC has a better performance of shortening the settling time while comparing with proportional controller and the traditional GPC.
3) The adaptive adjustment error model is used to reduce the effect of predictive error the GM(1,1) may produces. And to all of prediction models applying to the system, the adaptive adjustment error model can reduce the effect of predictive error the prediction models may produce.
4) Experimental results indicate that the compound control method based on adaptive fuzzy-grey predictive control and feedforward control (CAGPC) is feasible for stabilized and tracking platform system.
5) The compound control method based on adaptive fuzzy-grey predictive control and feedforward control (CAGPC) needs further improvement and experimental verification.
References
-
Erdal K., Okyay K. Grey prediction based control of a non-linear liquid level system using PID type fuzzy controller. IEEE 3rd International Conference on Mechatronics, Budapest, Hungary, July, 2006, p. 292-296.
-
Lv Wei, Guo Kong, Zhang Jian Feed-forward integrated with Fuzzy PID feedback current control algorithm in electric power steering. Transactions of the Chinese Society for Agricultural Machinery, Vol. 41, Issue 8, 2010, p. 10-15.
-
Ding Ke, Huang Yong, Ma Jia Error adaptive feedforward composite control of fast-steering-mirror. Chinese Journal of Lasers, Vol. 38, Issue 7, 2011, p. 1-6.
-
Zhu Ming, Liu Hui, Zhang Xin Adaptive feed-forward control for inertially stabilized platform. Optics and Precision Engineering, Vol. 21, Issue 5, 2013, p. 141-148.
-
Zhang Y., Zhang Shu, Qiao Yan Feed-forward control based on reference model disturbance observer of carrier-based opoelectronic theodolite. Optics and Precision Engineering, Vol. 21, Issue 5, 2013, p. 1213-1221.
-
Chen Yan, Luo An, Zhou Le A robust predictive deadbeat grid-connected control method based on power feed-forward control. Proceedings of the CSEE, Vol. 33, 36, p. 62-70.
-
Hao Shuang, Cai Yi, Zheng Wei Research on high-speed positioning of AC servo system based on feedforward control. Drive and Control, Vol. 2, 2010, p. 35-38.
-
Chung Chao, Chen Ho, Ting Ching Grey prediction fuzzy control for pH processes in the food industry. Journal of Food Engineering, Vol. 96, 2010, p. 575-582.
-
Wu Ye, Hu Wei, Xu Mei Linear model and improved method of disturbance rejection rate in seeker’s stability platform. Guidance and Fuze, Vol. 32, Issue 1, 2011, p. 1-5.
-
Tang Jian, Dong Yan, Zhao Ke μ syntehesis control of hydraulic Stewart platform based on dynamics disturbance feed forward. Journal of Jilin University, Vol. 39, Issue 3, 2009, p. 662-667.
-
Dai Wen, Xiong Wei, Yang Ai A kind of hybrid control algorithm for large time-delay system. Proceedings of 2011 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 2011, p. 803-806.
-
Bi Xiao, Yao Qiong A preliminary study on grey predictive control of industrial process. Journal of Southwest China Institute of Technology, Vol. 3, 1997, p. 11-16.
-
Wu H., Jiang C., Tai N., Hou Z. The application of grey neural network model to city electricity demand Forecasting. The Journal of Grey System, Vol. 4, 2004, p. 357-365.
-
Yang W., Liu S., Wang Y. The grey prediction of change trend of Chinese financial industry’s credit size. The Journal of Grey System, Vol. 1, 2006, p. 67-74.
-
Chen Z., Li L., Xiao X. GM(1,1) model and its application to controlling the inverted camber of widening concrete bridge. The Journal of Grey System, Vol. 4, 2006, p. 365-374.
-
Lu J., Wang C. M., et al. Residual GM(1,1) model-based prediction method for chaotic time series. The Journal of Grey System, Vol. 4, 2012, p. 379-388.
-
Truong D. Q., Ahn K. K. An accurate signal estimator using a novel smart adaptive grey model SAGM(1,1). Expert Systems with Applications, Vol. 39, 2012, p. 7611-7620.
-
Lu J., Xie W., Zhang A., Wang C. Chaos-based modified GM(1,1) power model in time series prediction. The Journal of Grey System, Vol. 26, Issue 4, 2014, p. 32-43.
-
Lu J., Xie W., Zhou H., Zhang A. Vibration suppression using fractional-order disturbance observer based adaptive grey predictive controller. Journal of Vibroengineering, Vol. 16, Issue 5, 2014, p. 2204-2215.
-
Kayacan E., Kaynak O. Single-step ahead prediction based on the principle of concatenation using grey predictors. Expert Systems with Applications, Vol. 38, 2011, p. 9499-9505.
-
Lu J. S., Wang C. M., Zhang A. J., Xie X. M. Residual GM(1,1) model-based prediction method for chaotic time series. The Journal of Grey System, Vol. 24, Issue 4, 2012, p. 379-388.
-
Lu J., Xie W., Zhou H., Zhang A. Design of a disturbance feedforward based grey predictive controller for stabilized platform system. The Journal of Grey System, Vol. 28, Issue 2, 2016, p. 64-75.
-
Wang X., Ji C., Zhou J., Jiang L., Gu B. Design and experiment of fruit and vegetable grasping system based on grey prediction control. Transactions of the CSAE, Vol. 26, Issue 3, 2010, p. 112-117, (in Chinese).
-
Zhang Y., Shao F., Wang J., Liu Y. Using a gray predictive model for controlling dynamic tension during cold rolling. Journal of Northeastern University, Natural Science, Vol. 32, Issue 5, 2011, p. 614-617, (in Chinese).
-
Huang S., Huang C. Control of an inverted pendulum using grey prediction model. IEEE Transactions on Industry Applications, Vol. 36, Issue 2, 2000, p. 452-458.
-
Zhang Guang, Fu Ying, Yang Ru Novel self-adjustable grey prediction controller. Control and Decision, Vol. 2, Issue 19, 2004, p. 212-215.
-
Meng Hong, Wang Chang, Zhang Ai, Bao Jian A novel adaptive grey predictive controller based on fractional-order improved disturbance observer and its application. The Journal of Grey System, Vol. 28, 2016, p. 90-105.
-
Lu Jian Reasearch on Attiude Measurement and Control Strategy of Stabilized Platform for Shiporne Weapon Aiming System. Doctoral Dissertation of Nanjing University of Science and Technology, NanJing, 2013.
-
Zhao W. Research on Position Control Algorithm Based on Pulse Train Control with Position Feedback and Feedforward Compensation. Master Thesis of Beijing Jiaotong University, Beijing, 2007.
-
Zhang B., Xi G. GM(1,1) model optimization based on the background value and boundary value correction. Systems Engineering-Theory and Practice, Vol. 33, Issue 3, 2013, p. 682-688.
-
Meng Hong, Wang Chang, Zhang Ai, Bao Jian A novel chaos times series prediction method and its application to carrier vibration interference attitude prediction of stabilized platform. Journal of Vibroengineering, Vol. 19, Issue 1, 2016, p. 562-576.
-
Jiang Bo, Chen Mian, Wang Bing, Zhou Chang Grey prediction neuron control of uncertain system with time delay. Systems Engineering and Electronics, Vol. 26, Issue 5, 2004, p. 644-646.
Cited by
About this article
The research is supported by the Open Project Program of Key Laboratory of Intelligent Perception and systems for High-Dimensional Information (Grant No. 30920130122005), the Key Laboratory of Intelligent Perception and Systems for High-Dimensional Information (Nanjing University of Science and Technology), Ministry of Education (No. JYB201609), and Research Fund for Doctoral Program of Higher Education of China (No. 20133219110027).
Meng Wang is mainly responsible for the writing of the paper and data simulation. He Zhang is mainly responsible for the review of the paper and the perfection of the theory. Xiaofeng Wang is mainly responsible for the improvement of the language organization and theory of the paper. Yunfeng He is mainly responsible for project communication and contact. Jianshan Lu is mainly responsible for the implementation of the experiment and data collection.
