Chaos control of a multi-dimensional chaotic mapping system by modified stability transformation method

1. Introduction

Chaos is an intrinsically complex phenomenon for deterministic nonlinear dynamical system. Generally, there are two complementary attributes to define chaos in both the temporal and spatial aspects: exponentially sensitive dependence on initial conditions, and pattern structure of strange attractors [1]. Due to its theoretical significance and engineering applicability, the chaos control has been paid extensive attention in diverse fields. Chaos control can catch the desired fixed points or periodic orbits embedded in the chaotic attractor of nonlinear dynamical system through implementing the target guidance and position. A key issue for chaos control is how to determine the control variable varying with time in terms of the past or present state, and incorporate it into a feedback term to achieve the purpose of controlling unstable periodic orbits (UPOs). Therefore, it is necessary to detect the UPOs of chaotic system in advance. However, detecting the UPOs of nonlinear systems with both numerical calculation and experimental implementation is one of the most challenging problems for nonlinear dynamics. Owing to the inherent unstable nature of UPOs, the analytic expressions for every periodic orbit cannot be obtained, only if the chaotic system is a simple nonlinear polynomial with low degree and the period of concern is low.

The most popular algorithm for detecting UPOs is Newton method (NT) [2], which has the second order convergence speed, but it is heavily dependent on the initial condition, as well as on the behavior of the partial derivatives. Further, the extended algorithms based on Newton method including relaxed Newton method [2, 3], parameter adjustment hybrid method [4] etc. have also local convergence. To overcome this limitation, the NT is combined with a global convergent method named stability transformation method (STM) to improve the convergent efficiency in this paper. From another perspective, Pyragas, et al. proposed and subsequently developed time-delayed feedback control (DFC) in a series of papers [5-7] to detect UPOs by stabilizing continuous chaotic system to period orbit. In addition, Parsopoulos et al. [8, 9] applied the stochastic optimization method (say, particles warm optimization) to locate chaotic system to high periodic orbits. Because this algorithm does not need the detailed information of initial condition and partial derivatives, it is an efficient alternative.

In order to locate chaotic system (including both discrete and continuous system) to an arbitrary UPO, Schmelcher and Diakonos [10-12] proposed the stability transformation method (STM), which does not require the specific information of target UPOs and has a global convergence. Meanwhile, it is worth noting that Kawai and Tsubone [18] developed a new control algorithm based on STM and DFC to control the UPOs by a simple circuit implementation. The author and partner [13] applied STM to stabilize a novel 3D autonomous chaotic system to multi-equilibrium. It is found that STM can be regarded as a special form of speed feedback control method, which facilitates the practical implementation of STM. In the subsequent paper [14], we further evaluated and compared the generality, efficiency and applicability of several popular chaos control approaches, and revealed the essential connections among these approaches. Recently, STM has been utilized to control the nonlinear iterative solution of First Order Reliability Method (FORM) [15-17]. Meng and Li [18] further expanded STM to the reliability-based design optimization which indicates that STM can greatly improve the optimization efficiency. Although STM has been widely used in chaos control, structure reliability and optimization design, the convergence speed is very slow when stabilized fixed points are around the static bifurcation points of chaotic system. In addition, the choices of stability matrix and relax parameter have direct influence on the performance of STM, and how to determine the optimal relax parameter and stability matrix that make STM be the fastest convergence speed remains to be further studied. Therefore, in this paper a novel modified STM is proposed to efficiently stabilize a 3D chaotic mapping system with various forms of bifurcations to stable fixed points.

Focusing on these problems aforementioned, this paper provides some new insights on stabilizing and controlling the unstable periodic fixed points of a 3D chaotic mapping system with various forms of bifurcations by modified STM. According to the information of unstable periodic fixed orbits, the stability matrix $C$, critical relax parameter $q_{crit}$ and optimal relax parameter $q_{opt}$ are derived respectively when STM satisfies given convergence condition. In order to overcome the disadvantage of slow convergence around the static bifurcation point, this paper combines STM with NT to stabilize chaotic system to any unstable periodic fixed point. Finally, the efficiency of improved STM is verified by numerical simulation. The aim of this work is to deepen the understanding for STM and promote its practical application.

2. Review of stability transformation method

In order to detect any UPO of chaotic system, Schmelcher and Diakonos [12] suggested an appropriate linear transformation to modify the eigenvalues of Jacobian matrix of dynamical system, and stabilize the original system to the unstable periodic fixed points without changing their value and location. The detailed introduction about STM can be referred to the literature [12].

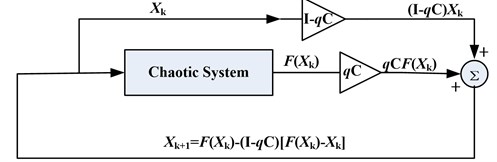
The expression of STM for controlled system is written as:

in which, $q$ is a relaxation parameter that has closely relationship with the eigenvalue of Jacobi matrix of original chaotic system and 0$<q<$ 1, and the stability matrix $C$ here is taken as $n\times n$ dimensional involutory matrix (namely, only one element in each row and each column in this matrix is 1 or –1, and the others is 0). Nevertheless, the later analysis in Section 5 indicates that non-involutory matrix can also achieve the objective of detecting unstable periodic fixed point. According to feedback control strategy, the corresponding block diagram for STM is displayed in Fig. 1.

From Eq. (1), it is easy to know that the STM neither requires the detail information of the target periodic fixed points nor calculates the Jacobian matrix of the system, namely the local information on the derivative of periodic fixed points. Therefore, it is a global convergent method and has low requirement for initial condition.

Fig. 1Control block diagram of STM

3. Stabilize unstable periodic fixed points of chaotic mapping system by STM

Consider the following 3D mapping system [19]:

where $a_1=$0.05, $a_2=$0.25, $a_3=$0.12, $b_1=$4.0, $c=$2.15, 0.4$\le b_2\le$1.2. Practically, the mapping system Eq. (2) can be viewed as a kind of nonlinear iterative procedure expressed as ${\mathbf{X}}_{k+1}=\mathbf{F}\left({\mathbf{X}}_k\right)$, which is adopted in many iterative algorithms for structural reliability assessment [15-17] and optimal deign [18]. The mapping system Eq. (2) does not always converge to some fixed point, and yield the phenomena of periodic oscillation, bifurcation and chaos with the control parameter $b_2$ varying in the interval [0.4, 1.2], which is indicated in Fig. 2(a). In order to clearly verify the type of the attractor, the three Lyapunov exponents (named $L_1$, $L_2$ and $L_3$) of the mapping system are also displayed in Fig. 2(b). It is demonstrated from Fig. 2(b) that when the control parameter $b_2<$0.544, $L_1$, $L_2$ and $L_3$ are less than zero, then the mapping system is stable and convergent to a fixed point. When the parameter $b_2\in$ [0.544, 0.683), the Lyapunov exponents $L_1=$0, $L_2<$0 and $L_3<$0, the attractor of the mapping system will change from a fixed point to a series limit cycles and then emerge a two-dimensional torus. However, the attractor will become a chaos while $L_1>$0, $L_2<$0 and $L_3<$0, especially become a super chaos with more than two Lyapunov exponents greater than zero.

Fig. 2a) Bifurcation plot of component y versus parameter b2; b) Lyapunov exponents versus b2 for three-dimensional mapping system

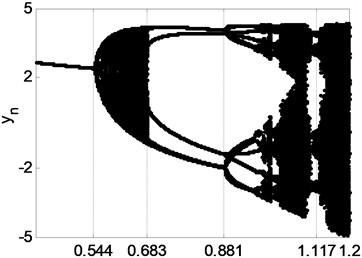
a)

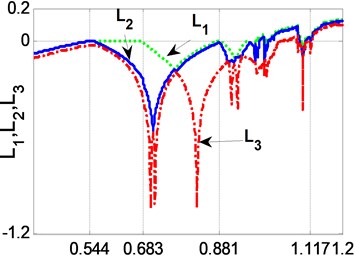
b)

3.1. Periodic-$\mathit{p}$ fixed points and bifurcation forms

Let:

3

${\mathbf{X}}_{k+p}=\left(\begin{array}{l}{x}_{k+p}\\ y_{k+p}\\ z_{k+p}\end{array}\right),\mathbf{F}\left({\mathbf{X}}_k\right)=\left(\begin{array}{c}{a}_1{x}_k+a_2{y}_k+a_3{y}_k^2\\ b_1-b_2{z}_k\\ c{x}_k\end{array}\right).$

The periodic-$p$ iterative mapping system can be written as:

4

${\mathbf{X}}_{k+p}={\mathbf{F}}^{\left(p\right)}\left({\mathbf{X}}_k\right).$

If Eq. (4) has fixed points, let $\mathbf{X}={\mathbf{X}}_{k+p}={\mathbf{X}}_k$, and substitute it to Eq. (3) and Eq. (4) respectively, and then all the analytical solutions of periodic-$p$ fixed points are obtained. Consequently, the explicit expression of the periodic-1fixed point with respect to parameter $b_2$ can be derived:

$y^{\left(1\right)}=\frac{a_1-1-a_2{b}_{2}c+b_{2}c\sqrt{(a_2-\frac{a_1-1}{b_{2}c}{)}^2-\frac{4a_3{b}_1(a_1-1)}{b_{2}c}}}{2a_3{b}_{2}c},$
$x^{\left(1\right)}=-\frac{y^{\left(1\right)}-b_1}{b_{2}c},z^{\left(1\right)}=-\frac{y^{\left(1\right)}-b_1}{b_2}.$

Similarly, the implicit expression of the periodic-2 fixed points with respect to $b_2$ is also achieved:

5

$A\left(b_2\right)(y^{\left(2\right)}{)}^4+B\left(b_2\right)(y^{\left(2\right)}{)}^3+C\left(b_2\right)(y^{\left(2\right)}{)}^2+D\left(b_2\right)y^{\left(2\right)}+E\left(b_2\right)=0,$
$x^{\left(2\right)}=\frac{b_1-y^{\left(2\right)}}{b_{2}c},z^{\left(2\right)}=a_{3}c(y^{\left(2\right)}{)}^2+\left(a_{2}c-\frac{a_1}{b_2}\right)y^{\left(2\right)}+\frac{a_1{b}_1}{b_2},$

in which:

$A\left(b_2\right)=c^3{a}_3^3{b}_2^3,B\left(b_2\right)=2c^3{a}_3^2{a}_1{b}_2^2,$
$C\left(b_2\right)=c^3{a}_3{a}_2^2{b}_2^3-2c^2{a}_3^2{b}_1{b}_2^2-2c^2{a}_3{a}_2{a}_1{b}_2^2+2c^2{a}_3^2{a}_1{b}_1{b}_2^2$
$-c^2{a}_3{a}_2{b}_2^2+c{a}_3{a}_1^2+c{a}_3{a}_1{b}_2,$
$D\left(b_2\right)=2c^2{a}_3{a}_2{b}_1\left(a_1-1\right)b_2^2-c^2{a}_2^2{b}_2^2+2c{a}_1{a}_2{b}_2-2c{a}_3{a}_1^2{b}_1{b}_2+2c{a}_3{a}_1{b}_1{b}_2+1$
$-a_1^{2}E\left(b_2\right)=c{a}_3{b}_1^2{b}_2-2c{a}_3{a}_1{b}_1^2{b}_2+c{a}_3{a}_1^2{b}_1^2{b}_2-c{a}_2{a}_1{b}_1{b}_2+c{a}_2{b}_1{b}_2+a_1^2{b}_1-b_1.$

The Jacobi matrix of mapping system at the fixed point ${\mathbf{X}}_k$ is expressed as:

6

$\mathbf{J}=\frac{\partial \mathbf{F}\left({\mathbf{X}}_k\right)}{\partial {\mathbf{X}}_k}=\left[\begin{array}{lll}\frac{\partial x_{k+1}}{\partial x_k}& \frac{\partial x_{k+1}}{\partial y_k}& \frac{\partial x_{k+1}}{\partial z_k}\\ \frac{\partial y_{k+1}}{\partial x_k}& \frac{\partial y_{k+1}}{\partial y_k}& \frac{\partial y_{k+1}}{\partial z_k}\\ \frac{\partial z_{k+1}}{\partial x_k}& \frac{\partial z_{k+1}}{\partial y_k}& \frac{\partial z_{k+1}}{\partial z_k}\end{array}\right]=\left[\begin{array}{lll}{a}_1& a_2+2a_3{y}_k& 0\\ 0& 0& -b_2\\ c& 0& 0\end{array}\right].$

The eigenvalues ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ of Jacobi matrix for mapping system with parameter $b_2$ can be obtained according to Eq. (6), which is displayed in Fig. 3. It is indicated from Fig. 3 that the module of eigenvalues are respectively equal or greater than one at the parameter $b_2=$0.544 and 0.605, and then the mapping system will emerge bifurcations. When $b_2=$0.544 (see Fig. 2(a)), the eigenvalues of Jacobi matrix at periodic-1 fixed point are gained:

${\lambda }_1=0.5113+0.8563i,{\lambda }_2=0.5113-0.8563i,{\lambda }_3=-0.9727.$

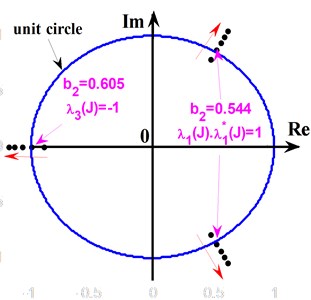
Then it is easy to get ${\lambda }_1\cdot {\lambda }_2=0.9978\approx 1$, and the two conjugate complex roots of eigenvalues will pass through unit circle as shown in Fig. 4, which implies that the mapping system produces Naimark-Sacker quasi-period bifurcation (see Fig. 2). Similarly, the eigenvalues of Jacobi matrix at periodic-1fixed point are obtained when $b_2=$0.605:

${\lambda }_1=0.5249+0.8799i,{\lambda }_2=0.5249-0.8799i,{\lambda }_3=-0.9999.$

Hence, the negative real eigenvalue ${\lambda }_3$ will pass through unit circle, demonstrating that the mapping system presents period-doubling bifurcation. Meanwhile, the solid line in Fig. 5 displays analytical solutions of periodic-2 fixed points for mapping system, which indicates that $b_2=$0.605 is the static bifurcation point of the mapping system.

Fig. 3Eigenvalue curves of mapping system

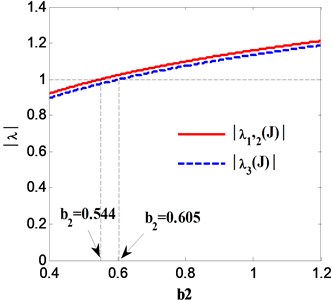
Fig. 4The forms of eigenvalues passing through unit circle

3.2. Stabilize unstable periodic fixed points by STM

With regard to periodic-$p$ fixed points of original mapping system, the control form of STM can be formulated as:

7

${\mathbf{X}}_{k+p}={\mathbf{X}}_k+q\mathbf{C}\left[{\mathbf{F}}^{\left(p\right)}\left({\mathbf{X}}_k\right)-{\mathbf{X}}_k\right].$

Taking periodic-2 fixed points as example, all the analytical solutions of periodic-2 fixed points for mapping system are obtained from Section 3.1, as solid lines shown in Fig. 5. It is indicated that the number of analytical solutions for periodic-2 fixed point change from one to three with the parameter $b_2$, i.e. static bifurcation emerges. In order to detect all the periodic-2 points with STM, it is required to choose different involutory matrix $\mathbf{C}$ (i.e. the different stability transformation systems) and initial points in the basin of chaotic attractor. The system parameter $b_2$ changes in the interval [0.4, 1.2]. As for every stability transformation system with appropriate relaxation parameter $q$, an initial point is suitably selected in the chaotic attractor and the STM is performed. Then the $N$th iterative solution is compared with the exact periodic-2 point, as dashed lines displayed in Fig. 5. From Fig. 5, some interesting conclusions are obtained as follows:

1) The required iterative number $N$ will decrease with relax parameter $q$, but less unstable fixed points can be detectable by STM. Taking the stability matrix ${\mathbf{C}}_1=\mathbf{I}$ and initial condition ${\mathbf{X}}_{02}$(–3,1,0), when $q=$0.1, the $N_1=$2000th iterative value of $y$ component always converge to the upper branch of analytical fixed points (see red dashed line in Fig. 5(a)). However, while $q=$ 0.6, the $N_2=$500th iterative value of $y$ component jump from the upper branch to the lower one with system parameter $b_2$ increasing in the interval [0.4, 1.2]. Especially, when $b_2>$1.144, the iterative value of $y$ component will generate oscillation and could not converge to the corresponding analytical fixed points (see red dashed line in Fig. 5(b)).

2) Keeping the initial points unchanged, STM can stabilize the mapping system to the same or distinct analytical fixed points by choosing different stability matrix. Taking the initial point ${\mathbf{X}}_{02}$(–3, 1, 0) and $q=$0.6, when the stability matrix ${\mathbf{C}}_1=\mathbf{I}$, the iterative value of $y$ component converges to the upper branch of analytical fixed points with $b_2$ varying in the interval [0.4, 0.98], but to the lower branch with $b_2$ varying in the interval [0.98, 1.144] (see the red dashed line in Fig. 5(b)). However, when the stability matrix ${\mathbf{C}}_3=$ [0 1 0; –1 0 0; 0 0 1], the iterative value of $y$ component converges to the lower branch of analytical fixed points with $b_2$ varying in the whole interval [0.4, 1.2] (see the blue dot dashed line in Fig. 5(b)).

3) Keeping stability matrix $\mathbf{C}$ unchanged, STM can stabilize the mapping system to distinct analytical fixed points by choosing different initial points. Adopting stability matrix ${\mathbf{C}}_1=\mathbf{I}$ and relax parameter $q=$0.1, when the initial points are taken as ${\mathbf{X}}_{01}$(0,0,0) and ${\mathbf{X}}_{02}$(–3,1,0), the iterative value of $y$ component respectively converges to the lower and upper branch of analytical fixed points with $b_2$ varying in the interval [0.4, 1.2] (see blue dotted and red dashed lines in Fig. 5(a)).

Fig. 5STM control of period-2 fixed points for mapping system when b2 varying in the interval [0.4, 1.2] a) C1=I, C2= [0 0 0;0 1 0;1 0 0], X01= (0,0,0); b) C3= [0 1 0; –1 0 0;0 0 1], X02= (–3,1,0)

4. Convergence analysis for STM

The essence of STM is to introduce an appropriate linear transformation to modify the eigenvalues of Jacobian matrix for original chaotic system, and stabilize to the unstable periodic fixed points without changing their value and location. The Jacobi matrix ${\mathbf{J}}^{*}$ of STM for transformed system is expressed as:

in which $\mathbf{J}$ is the Jacobi matrix of the original mapping system. As for periodic-2 mapping system, the Jacobi matrix $\mathbf{J}$ can be attained:

It is known from Eq. (8) that, if the spectral radius of matrix ${\mathbf{J}}^{*}$ is less than 1 (i.e., $\rho \left({\mathbf{J}}^{*}\right)<$1), STM will converge to periodic fixed point of original system. However, in contrast if the spectral radius of matrix ${\mathbf{J}}^{*}$ is more than 1 (i.e., $\rho \left({\mathbf{J}}^{*}\right)>$1), STM does not converge and will generate undesired oscillation. Fig. 6 demonstrates three eigenvalue curves of Jacobian matrix for different stability transformation systems which coincides well with the convergence property of the curves in Fig. 5. In addition, it is found that when the parameter $b_2=$0.605, the spectral radius of the Jacobi matrix for STM is always close to 1 (i.e., $\rho \left({\mathbf{J}}^{*}\right)\approx$1) no matter how the parameter $q$ and matrix $\mathbf{C}$ are selected. This implies that $b_2=$0.605 is a critical parameter that corresponds to the static bifurcation point of original mapping system.

Fig. 6Eigenvalue curves of stability transformation system when a) C=C1, q=q3; b) C=C2, q=q2; c) C=C3, q=q3

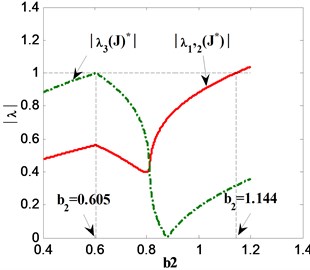
a)

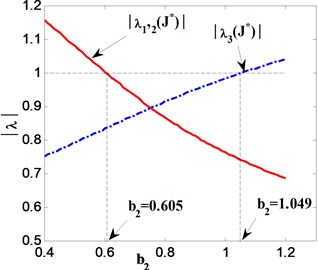
b)

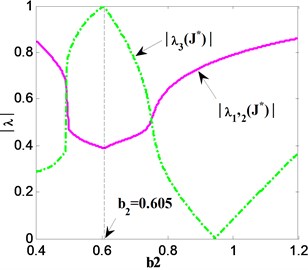
c)

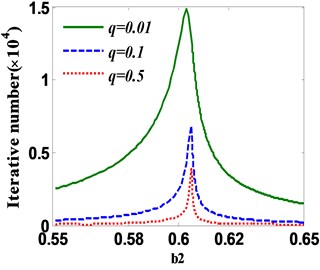
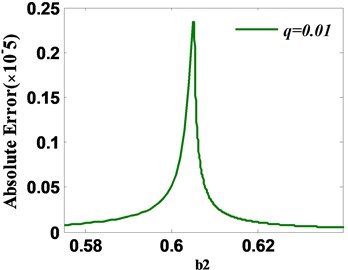
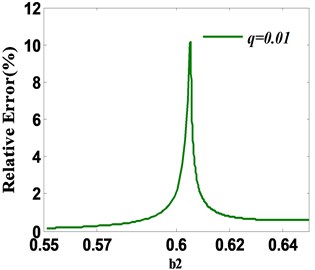
When the system parameter $b_2=$0.605 (i.e. the static bifurcation point of original system), the spectral radius of stability transformation system $\rho \left(\mathbf{J}\right({\mathbf{X}}^{\mathbf{*}}\left)\right)\approx \rho \left({\mathbf{J}}^{\mathbf{*}}\right({\mathbf{X}}^{\mathbf{*}}\left)\right)\approx 1$ and therefore the convergence speed of STM is very slow around the static bifurcation point. It is supposed that the iteration of STM stops when the absolute error of sequential iterative values satisfies $‖{\mathbf{X}}_{k+1}-{\mathbf{X}}_k‖\le$ 10^-5. Fig. 7(a) displays the required iterative number when STM satisfies convergence condition with different relax parameter $q$. It is indicated from Fig. 7(a) that the maximum iterative number by STM occurs around the static bifurcation point $b_2=$0.605, which is consistent with the theoretical analysis. Furthermore, the smaller the parameter $q$ is, the more iterative number required by STM is. When $q\to$0, the required iterative number $N\to \infty$. In addition, Fig. 7(b) and Fig. 7(c) respectively demonstrate the absolute errors and relative errors between iterative solution and periodic fixed point when STM (initial point ${\mathbf{X}}_{02}$ and stability matrix ${\mathbf{C}}_3$) satisfies convergence condition (≤ 10^-5) with relax parameter $q=$0.01. It is observed that the maximum absolute and relative errors happen at the bifurcation point $b_2=$0.605. Specifically, when the relax parameter $q=$0.01, the maximum absolute error $‖{\mathbf{X}}_{k+1}-{\mathbf{X}}^{*}‖=$ 0.2337×10^-5 and the maximum relative error$‖\frac{{\mathbf{X}}_{k+1}-{\mathbf{X}}^{\mathbf{*}}}{{\mathbf{X}}^{*}}‖\times \text{100 \%}=$ 10.17 %. Therefore, it is worth noting that detecting unstable periodic fixed points of chaotic system requires careful concern on the bifurcation point owing to the slow convergence of STM.

Fig. 7a) Iterative numbers; b) absolute error between iterative solution and fixed point; c) relative error between iterative solution and fixed point for STM with varying q

a)

b)

c)

5. Determination of stability matrix $\mathbf{C}$ and relaxation parameter $\mathit{q}$

5.2. Determination of critical parameter ${\mathit{q}}_{\mathit{c}\mathit{r}\mathit{i}\mathit{t}}$ and optimal parameter ${\mathit{q}}_{\mathit{o}\mathit{p}\mathit{t}}$

The prominent advantages of STM as compared with other chaos control algorithms are the global convergence property, the low requirement for initial point and fast speed convergence to linear domain of periodic fixed point. However, the rate of convergence will be slow when iterative values are located in linear domain of periodic fixed point. To overcome this limitation, in terms of whether the information of periodic fixed points are known or not in advance, this paper will improve the performance of STM from two aspects as followings

For the information of periodic fixed points to be stabilized is known in advance, increase relax parameter $q$ and the convergence speed will be faster. However, STM will not converge sometimes if $q$ is too large. Hence, we should determine an optimal $q_{opt}$that makes STM converge fastest to periodic fixed point.

For the unknown information of periodic fixed points, we can combine STM with NT to improve the computational efficiency of STM.

As aforementioned, the relax parameter $q$ of STM is closely related to the stability property of the periodic fixed points. As for a periodic fixed point, there exists a critical parameter $q_{crit}$ which make the controlled system be at the boundary of stability and instability, namely the module of the maximum eigenvalue of the Jacobi matrix ${\mathbf{J}}^{\mathbf{*}}$ be equal to 1. It is obtained from Eq. (9):

12

$\left|{\lambda }_i^{*}\right|=\left|1+q{\delta }_i({\lambda }_i-1)\right|\le 1,i=\mathrm{1,2},\dots .,n.$

Let ${\lambda }_i=a_i+i{b}_i$ and substitute it into Eq. (12) and the following module is achieved:

13

$\left|{\lambda }_i^{*}\right|=\left|1+q{\delta }_i(a_i-1)+i{\delta }_{i}q{b}_i\right|\le 1\Rightarrow [1+q{\delta }_i(a_i-1){]}^2+q^2{b}_i^2\le 1,i=\mathrm{1,2},\dots ,n$

in which 0 $<q<$1, ${\delta }_i$ is presented in Eq. (11). From Eq. (13), the formula of parameter $q$ is further attained:

$\Rightarrow q\le \underset{i=\mathrm{1,2}\cdots ,n}{\mathrm{i}\mathrm{n}\mathrm{f}}\left(\frac{-2{\delta }_i\left(a_i-1\right)}{(a_i-1{)}^2+b_i^2}\right)=\underset{i=\mathrm{1,2}\cdots ,n}{\mathrm{i}\mathrm{n}\mathrm{f}}\left(\frac{2\left|a_i-1\right|}{(a_i-1{)}^2+b_i^2}\right).$

Accordingly, the critical value $q_{crit}$ is written as:

14

$q_{crit}=\underset{i=\mathrm{1,2}\cdots ,n}{\mathrm{i}\mathrm{n}\mathrm{f}}\left(\frac{2\left|a_i-1\right|}{(a_i-1{)}^2+b_i^2}\right).$

Again, take periodic-2 fixed points of controlled mapping system as an example. It is seen from Fig. 5(b) and Fig. 6(a) that when ${\mathbf{C}}_1=\mathbf{I}$, $q=$0.6, the module of the maximum eigenvalue of Jacobi matrix ${\mathbf{J}}^{*}$ of transformed system Eq. (7) with system parameter $b_2=$1.144 is approximate equal to 1. That is to say, $q=$0.6 is the critical value of STM at the system parameter $b_2=$1.144. On the other hand, when the mapping system parameter $b_2=$1.144, the analytical periodic-2 fixed point for mapping system can be acquired form implicit expression Eq. (5) and then substituted into Eq. (9), so the corresponding eigenvalues of Jacobi matrix ${\mathbf{J}}^{*}$ are obtained:

${\lambda }_1^{*}=0.5984+1.0846i,{\lambda }_2^{*}=0.5984-1.0846i,{\lambda }_3^{*}=-1.1944.$

In terms of Eq. (14) the critical value $q_{crit}$ is calculated:

$q_{crit}=\underset{i=\mathrm{1,2},3}{\mathrm{i}\mathrm{n}\mathrm{f}}\left(\frac{2\left|a_i-1\right|}{(a_i-1{)}^2+b_i^2}\right)=0.6005.$

Which is in agreement with predefined value $q_{crit}=$0.6.

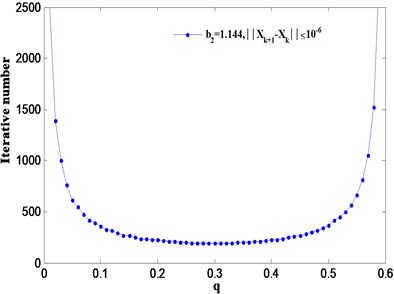
Clearly, the convergence speed of STM becomes very slow when $q$ is close to the critical parameter $q_{crit}$, and the transformed system is at the boundary of stability and instability. Fig. 8 illustrates the required iterative number when STM (in which $b_2=$1.144, $\mathbf{C}=\mathbf{I}$ and ${\mathbf{X}}_0$(–3,1,0)) satisfies convergence condition with relax parameter $q$ varying in the interval (0, $q_{crit}$). It is demonstrated from Fig. 8 that the iterative number versus $q$ presents approximately an U-type curve, and when the relaxation parameter $q$ is close to zero or critical value $q_{crit}$ respectively, the required iterative number tends to infinity, i.e. theoretically $\rho \left({\mathbf{J}}^{*}\right)=$1. Therefore, there exists an optimal value $q_{opt}$ for the parameter $q$ in the interval 0 $<q<q_{crit}$ which makes the required iterations be the least. It is seen that the U-type curve changes slightly nearby $q=q_{crit}$/2 = 0.3, thus here the optimal parameter $q_{opt}$ is set as:

15

$q_{opt}\approx \frac{q_{crit}}{2}=\underset{i=\mathrm{1,2}\cdots ,n}{\mathrm{i}\mathrm{n}\mathrm{f}}\left(\frac{\left|a_i-1\right|}{(a_i-1{)}^2+b_i^2}\right).$

Fig. 8Iterative numbers for STM when q varying in the interval (0, qcrit)

Nevertheless, in most instances the information of periodic fixed points are unknown in advance, and the exact optimal parameter $q_{opt}$ could not be determined. For this situation, this paper combines STM with NT to stabilize periodic fixed points. Firstly, a small enough parameter $q$ is taken and a set of initial points and involutory matrix ${\mathbf{C}}_i$ are chosen. Next, STM is conducted until the absolute error of sequential iterative points satisfies a given value $‖{\mathbf{X}}_{k+1}-{\mathbf{X}}_k‖\le \epsilon$ ($\epsilon \approx$ 0.01~0.1). In this way, the iterative value has been in linear domain of periodic fixed point. Given the fact that Newton method has the second order convergence speed at the linear domain of initial condition, the iterative value $X_k$ of STM can be taken as the initial point of Newton method and continue to conduct the iteration until satisfying the convergent condition. It is pointed out that in order to enlarge the linear domain, a relaxation factor can be introduced for NT, i.e. the relaxed Newton method can be taken as an alternative [14]. In practice, the NT is written as:

16

${\mathbf{X}}_{k+p}={\mathbf{X}}_k-D{\mathbf{G}}^{-1}\left({\mathbf{X}}_k\right)\cdot \mathbf{G}\left({\mathbf{X}}_k\right)={\mathbf{X}}_k-(\stackrel{-}{\mathbf{J}}-\mathbf{I}{)}^{-1}\cdot \left({\mathbf{F}}^p\left({\mathbf{X}}_k\right)-{\mathbf{X}}_k\right),$

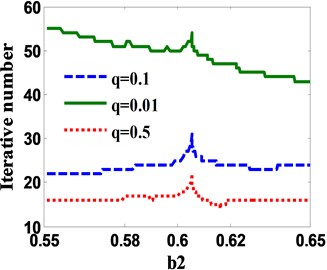
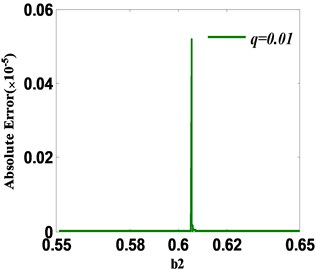
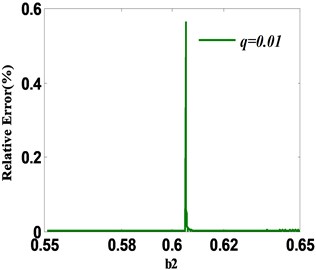
where, ${\mathbf{X}}_k$ is the $k$th iterative point of STM which satisfies the given convergent condition, and $\mathbf{G}\left({\mathbf{X}}_k\right)={\mathbf{F}}^p\left({\mathbf{X}}_k\right)\mathbf{˗}{\mathbf{X}}_k$, $\stackrel{-}{\mathbf{J}}=\partial {\mathbf{F}}^p\left({\mathbf{X}}_k\right)/\partial {\mathbf{X}}_k$, $D\mathbf{G}\left({\mathbf{X}}_k\right)=\stackrel{-}{\mathbf{J}}-\mathbf{I}$. The iterative value will converge to the desired periodic fixed point in a high precision with a small number of iterations. Fig. 9(a) shows the required iterative number versus system parameter $b_2$ by the combination of STM and NT. Compared with Fig. 7(a), the efficiency is improved considerably. Meanwhile, the corresponding absolute and relative errors between iterative solution and fixed point are displayed in Fig. 9(b) and Fig. 9(c). When the relax parameter $q=$0.01, the maximum absolute error $‖{\mathbf{X}}_{k+1}-{\mathbf{X}}^{\mathbf{*}}‖=$ 0.1298×10^-5 and the maximum relative error $‖\frac{{\mathbf{X}}_{k+1}-{\mathbf{X}}^{\mathbf{*}}}{{\mathbf{X}}^{\mathbf{*}}}‖\times \text{100}\text{\%}=$ 0.56 % which are remarkably decreased compared with those in Fig. 7(b) and Fig. 7(c). However, the most iterative number, the maximum absolute and relative errors still happen at the static bifurcation point of original mapping system.

Fig. 9a) Iterative numbers; b) absolute error between iterative solution and fixed point; c) relative error between iterative solution and fixed point when converging to fixed point using STM-NT

a)

b)

c)

6. Conclusions

For deeply understanding the numerical performance of STM for chaos control of nonlinear dynamical system and convergence control of engineering iterative systems, several associated issues of STM is thoroughly studied.

Firstly, a 3D chaotic mapping system with various forms of bifurcations is taken as an example in this paper and the effects of three factors of STM such as initial condition, stability matrix $C$ and relaxation parameter $q$ on the capability of control algorithm are investigated in detail. It is found that the required iterative number $N$ will decrease with relax parameter $q$, but less unstable fixed points can be detectable by STM. Especially, the stabilized periodic fixed point by STM will jump from one branch to another of analytical fixed point even if selecting the same relax parameter, initial condition and stability matrix (as red dashed line shown in Fig. 5(b)). The other detailed conclusions can be seen in Section 3.2.

Next, the eigenvalue curves of Jacobian matrix for different stability transformation systems are investigated. It is revealed that the maximum iterative number for STM occurs around the static bifurcation point, and thus the convergence speed of STM is very slow and hard to converge. Meanwhile, the absolute and relative errors between iterative solution and periodic fixed point with different relax parameter $q$ are demonstrated respectively when STM satisfies convergence condition (≤ 10^-5). It is observed that the maximum absolute and relative errors happen at the bifurcation point.

At last, according to the information of unstable periodic fixed point, the stability matrix of STM is derived for three different cases. However, in some situation the matrix $C$ is unnecessarily taken as involutory matrix depending on the Jacobian matrix of original dynamical system, which sheds a new light on the development of STM. Meanwhile, the critical parameter $q_{crit}$ on the basis of stability matrix $\mathbf{C}$ in STM are determined. It is found that the iterative number versus $q$ presents approximately a U-type curve, and the smaller or the closer to the critical parameter $q_{crit}$ the relax parameter $q$ is, the slower the rate of convergence of STM is. Moreover, the optimal parameter $q_{opt}$ in the interval (0, $q_{crit}$) that makes the required iterations by STM be the least is obtained. When a priori information of the periodic fixed point is unknown in advance, STM is combined with NT to overcome the disadvantage of slow convergence around the static bifurcation point.