Abstract
The present paper involves in the estimation and approximation of Eigen values and Eigen vectors of an Elliptical plate with a rectangular cut-out under simply supported boundary condition using Independent coordinate coupling method with an eight term deflection function. The study also investigates the effect of position and size of cut-out with rectangular shape on the natural frequencies of an elliptical plate. The variation of the natural frequencies with the change in position of cut-out along the axes of symmetry and along the radial line is studied. The present method ICCM utilizes independent coordinates separately for plate domain and hole domain. The deflection condition of plate and the hole is equated to derive the relationship between global axes and the local axes. The resulted transformation is useful in deriving the mass and stiffness matrices. The size and position of cut-out have been focused to investigate their effect on the natural frequency of an elliptical plate.
1. Introduction
Elliptical shaped plates have wide applications in the field of Aeronautics, Marine and civil Engineering, hence the knowledge of the vibration of an elliptical plate is essential. In engineering applications, a plate is often required to accommodate mountings or accessories, therefore a plate with holes is commonly occurring structure. Therefore, knowledge of free vibration of plates with different shaped cut-outs at different positions is essential. Rayleigh-Ritz method is one of the method to derive the frequencies if plate and the hole geometries are same, whereas it cannot be easily applied if the geometry of plate and the hole is different. Here the present ICCM is an effective tool to overcome this, and works well by matching the deflection condition between the plate and hole.
The fundamental frequency parameters of an elliptical plate are obtained by several authors using different approaches that can be found in the references [1-8]. K. L. Prasad [1] provided reliable approximate formulae for simply supported and clamped elliptical plates by following the Rayleigh-Ritz method with a three-term deflection function. A. W. Leissa [2] worked on simply supported elliptical plates using Rayleigh-Ritz method to obtain accurate fundamental frequencies. Maurizi [3] derived an approximate expression for the fundamental frequency of vibration of elastic plates under clamped condition. K. Y. Lam [4] etc. Proposed a general numerical method to estimate the natural frequencies for elliptical plates by introducing a set of orthogonal plate functions as an admissible function in Rayleigh-Ritz method. Y. Shibaoka [5] investigated the fundamental normal mode of the transverse vibration of clamped elliptical plate using Mathieu functions and modified Mathieu functions in an exact manner. R. P. Mcnitt [6] worked on vibration of elliptical plate by assuming classical small-deflection theory is valid and computed the natural frequencies a clamped elliptical plate using an ordinary product solution and the Galerkin method. Moon K. Kwak, Sangbo Han, [8] investigated the Free vibration analysis of rectangular plate with a hole by means of Independent coordinate coupling method, in which the energies corresponding to the hole and plate were derived independently, and applied to circular cut-outs effectively. K. Torabi, A. R. Azadi, [9] applied the Raleigh-Ritz method to find the transverse vibrations of rectangular plate with circular central hole having a point support. Paramasivam [10] applied the finite difference method in the analysis of a simply-supported and clamped rectangular plate with a rectangular hole. Hegarty and Ariman [11], Eastep and Hemmig [15] applied the point-matching method in the analysis of a rectangular plate with a circular cut-out. Aksu and Ali [12] also applied the finite difference method to analyze a rectangular plate with more than two holes. Rajamani and Prabhakaran [13] assumed that the effect of a hole is equivalent to an externally applied loading and carried out a numerical analysis based on this assumption for a composite plate. Rajamani and Prabhakaran [14] investigated the effect of a cut-out on the natural vibration characteristics of an isotropic and orthotropic plates under simply-supported and clamped boundary conditions.
So far in the literature survey the authors came across the free vibration analysis of an elliptical plate with various approaches. But in the present paper the authors contributed their efforts to predict, how the natural frequency of an elliptical plate with cut-out is varying due to the change in position and size of the cut-out using a newly developed technique called independent coordinate coupling method, to the best of knowledge which is so far not discussed in the earlier. The analysis by varying the position of the cut-out along the axis of symmetry and along a radial line of the plate using the ICCM method is presented.
2. Free vibration of an elliptical plate
An elliptical plate is assumed which lies in an - plane, having dimensions of as shown in the figure. Semi-major axis in the -direction and semi minor axis in the direction. The analysis begins with applying the Raleigh’s method in which the maximum kinetic energy is equals to maximum potential energy of a vibrating structure. In the expressions of and the deflection function is assumed in such a manner that it has to satisfythe boundary condition of the plate. Using of non-dimensional variables leads to the geometrical limits of plate, ‘0’ to ‘1’. In solving the equations, frequency parameter is obtained which relates the dimensionalized frequency to Non-dimensionalized frequency. It is as follows.
Fig. 1Elliptical plate
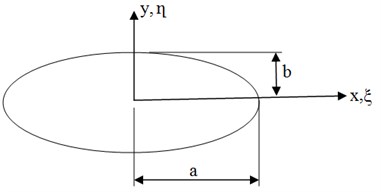
The boundary of an elliptical plate is expressed as:
where, and are non-dimensional variables.
The maximum kinetic energy and the maximum strain energy of an elliptical plate is expressed as:
Assuming simple harmonic motion and equating the maximum strain energy of the plate to its maximum kinetic energy, one obtains in terms of non-dimensional variables as:
where frequency parameter , aspect ratio , , flexural rigidity – , is thickness of plate, mass density, – Poisson’s ratio, – Young’s modulus, – circular frequency
For a simply supported elliptical plate, eight term deflection functions for ‘’ are chosen as:
where , the deflection function in the Eq. (3) satisfies the boundary condition with zero edge deflection along the boundary of the plate and () are Eigen vectors of a corresponding Eigen value which are used to plot the mode shape of the natural frequency.
The number of terms in the deflection function will be varied according to the aspect ratio of the plate to be considered. A least upper bound on the frequency is obtained by minimizing Eq. (2) with respect to coefficients . Substituting Eq. (3) in to Eq. (2) and carrying out the differentiation with respect to one obtains eight homogenous equations in , it can be formulated as:
For a non-trivial solution, the determinant of the coefficient matrix is equated to zero:
Here the matrices and are symmetric and both are of order eight with positive definite. The components of these matrices are presented in the Appendix A and Appendix B.
The Eigen values of an elliptical plate can be derived using Eq. (5) and the corresponding Eigen vectors can be plotted using Eq. (3-4). The smallest root of the characteristic Eq. (5) gives the square of the fundamental frequency parameter.
3. ICCM for an elliptical plate with a rectangular hole
Let us consider an elliptical plate with a central rectangular hole as shown in the Fig. 2. Considering the non-dimensionalised coordinates as:
and the displacement inside the hole can be expressed as:
Which is considered in the -direction of the plane while plotting the mode shape, where is the admissible function matrix and is the generalized coordinate vector. The admissible function with separation of variables is expressed as follows:
where, is defined as number of terms required for the convergence of solution and is the assumed deflection function as in -direction in such a way that it has to satisfy the boundary condition of rectangular plate under simply supported condition, similarly is in -direction. And the conversion of non-dimensional variables between the global axes and the local axes will be discussed in the following sessions.
Fig. 2Elliptical plate with a rectangular hole with local axes
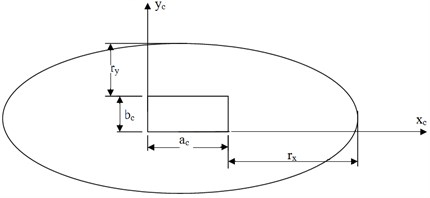
The kinetic energy and the strain energy of a rectangular plate is expressed as:
Substituting the Eqs. (6), (7) in (9) and solving the following relations are obtained:
Hence the total kinetic and potential energies can be written as:
In which:
where
And equating the maximum strain and kinetic energy gives the Raleigh’s quotient: , where is the non-dimensionalized natural frequency, having the relationship with the natural frequency.
Note that the definite integrals in Eq. (13) has distinctive advantage that it has an integral limit from 0 to 1 thus permitting closed form expressions. The displacement matching condition between the global and local coordinates should be satisfied inside the hole domain. Hence it can be expressed as:
The relationship between the non-dimensionalized global and local coordinates can be written as:
These relations will be used for the transformation in Eq. (8) as discussed in the earlier. Considering Eqs. (3), (7), (8) and inserting them in to Eq. (14) we can derive:
In the above mathematical expression, it is expressed that deflection of hole is equals to deflection of plate. Multiplying Eq. (16) by and performing integration, we can derive:
Using the orthogonal property of the Eigen functions of the uniform beam, Eq (17) can be rewritten as:
If we express Eq (18) in the matrix form, we can have:
where is the transformation matrix between two coordinates. Inserting Eq. (19) in to Eq. (11), we can derive:
where:
Above equations can be expressed in the form of non dimensionalized parameters:
where:
where: and .
Hence, the non-dimensionalized Eigen value problem can be expressed as:
In deriving the mass and stiffness matrices, Eq. (23) for the Eigen value problem, we only needed the transformation matrix,. and can be easily computed using the Eq. (5) Compared to the approach based on the global coordinates, the numerical integration for the transformation matrix, , is easy because of the integral limits. The ICCM enables us to solve the free vibration problem of the elliptical plate with rectangular hole more easily.
4. Numerical results
Numerical calculation started with finding the Eigen values and Eigen vectors of an elliptical plate considering the aspect ratio 0.5 with various terms until the convergence of solution is reached and the solutions are validated with the available literature.
Table 1Convergence of fundamental frequency parameter, ωb2ρh/D for a simply supported elliptical plate with b/a= 0.5 and υ= 0.25
No. of terms in Eq. (3) | Solution from Eq. (5) | Reference (1) | % error |
5 | 3.3057 | ||
6 | 3.2832 | ||
7 | 3.2832 | ||
8 | 3.2831 | 3.281 | 0.06 % |
9 | 3.2831 | ||
11 | 3.2831 | ||
12 | 3.2831 |
The data from the Table 1 concludes that the solution is stable with eight terms of deflection function and the obtained solution is very much closer to the solution available in reference [1]. Whereas in the reference [4] a stable solution is obtained for 80 terms, which requires more computational time than the time required to compute 8 terms, hence it is evident that using the present ICCM method, computational time is reduced.
Now the problem is extended to the title, by inserting a rectangular cut-out with a dimension of located at the center of the plate. The independent coordinate coupling method is used for the analysis of free vibration under simply supported boundary condition by taking .
The obtained results are tabulated in Table 2 and validated using ANSYS, since the case of an elliptical plate with a rectangular hole cannot be easily handled by the Raleigh-Ritz method due to the geometry difference of plate and hole.
Table 2The Frequency parameter, ωb2ρh/D for a simply supported elliptical plate (b/a= 0.5) with a hole (0.2×0.1) at υ= 0.3
Mode sequence number | Solution from Eq. (24) | Ansys (non-dimensional) | % error |
1 | 3.2735 | 3.2768 | 0.1 |
2 | 5.9195 | 5.9237 | 0.07 |
3 | 9.5726 | 9.5741 | 0.015 |
4 | 11.5228 | 11.524 | 0.01 |
5 | 14.4224 | 14.4239 | 0.01 |
6 | 15.6364 | 15.638 | 0.01 |
The authors are also interested to know the variation of fundamental frequency due to the change in position of hole. In this regard, the position of a square hole of dimensions (0.1×0.1) is varied along the axis symmetry of plate and along the radial line of the elliptical plate as shown in the Fig. 3 and Fig. 4. The results are tabulated in the Table 3 and Table 4. The variation of fundamental frequency due to the change in position of hole along the axis of symmetry and along a radial line of the plate is plotted in the Fig. 5.
Fig. 3Elliptical plate with a square hole on major axis
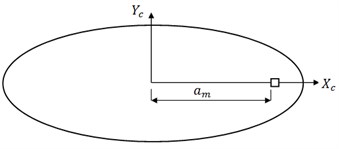
Fig. 4Elliptical plate with a square hole on radial line
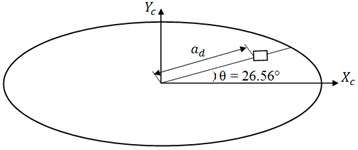
Table 3SSSS, Values of the frequency coefficients in the case of an Isotropic elliptical plate when the position of a cut-out is displaced along the axis of symmetry of the plate (b/a= 0.5) with a hole (0.1×0.1) at υ= 0.3
Hole position on major axis line, | ||||||
0.15 | 3.2949 | 5.91424 | 9.599342 | 11.53104 | 14.39573 | 15.66805 |
0.3 | 3.296872 | 5.905612 | 9.606326 | 11.5294 | 14.40476 | 15.67791 |
0.45 | 3.299255 | 5.901504 | 9.58866 | 11.52981 | 14.42489 | 15.67627 |
0.6 | 3.301391 | 5.90438 | 9.574692 | 11.53145 | 14.38792 | 15.67298 |
0.75 | 3.302993 | 5.910131 | 9.582908 | 11.5331 | 14.37724 | 15.67586 |
0.9 | 3.303856 | 5.913829 | 9.595233 | 11.53392 | 14.40559 | 15.67955 |
Table 4SSSS, Values of the frequency coefficients in the case of an Isotropic elliptical plate when the position of a cut-out is displaced along a radial line of the plate
Hole position on radial line | ||||||
0.1 | 3.2949 | 5.9171 | 9.592768 | 11.52365 | 14.41093 | 15.66394 |
0.2 | 3.2964 | 5.9125 | 9.602217 | 11.5142 | 14.39696 | 15.66148 |
0.3 | 3.2984 | 5.9093 | 9.604682 | 11.50968 | 14.40394 | 15.64546 |
0.4 | 3.3004 | 5.9088 | 9.599752 | 11.51297 | 14.4175 | 15.63149 |
0.5 | 3.3022 | 5.9117 | 9.595644 | 11.52036 | 14.41791 | 15.63724 |
0.6 | 3.3036 | 5.9154 | 9.597698 | 11.52734 | 14.41298 | 15.65696 |
To show how the fundamental frequency is varying due to the change in position of a cut-out along the axis of symmetry and along the radial line of plate, the Fig. 5 graph is plotted using the data from Table 3 and Table 4.
Using Eq. (4) the mode shape is plotted to a known frequency, to show how the structure is vibrating for the corresponding frequency. The mode shapes obtained from analytical MATLAB and a software ANSYS are compared in the Fig. 6.
Fig. 5the variation of fundamental frequency due to the positional change of hole along the axis of symmetry and along a radial line
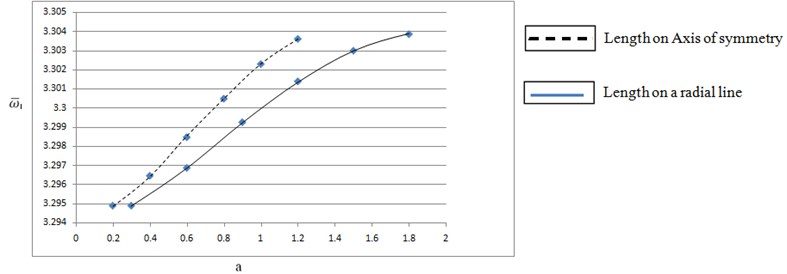
Fig. 6Comparison of mode shapes plotted in ANSYS and MATLAB
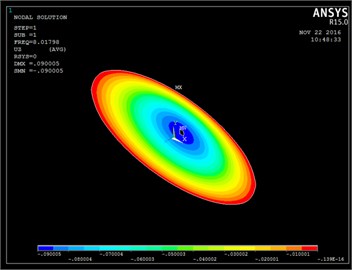
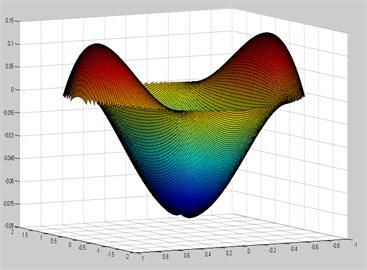
a) Modeshape 1 (ANSYS)
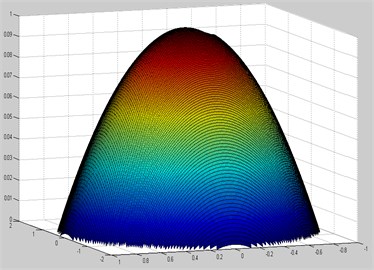
b) Modeshape 1 (MATLAB)
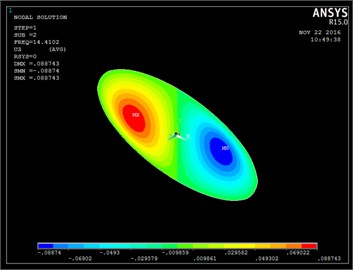
c) Modeshape 2 (ANSYS)
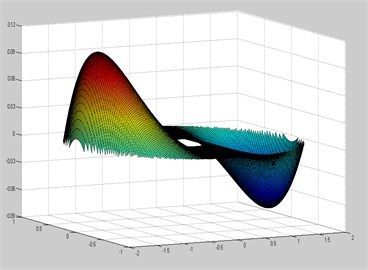
d) Modeshape 2 (MATLAB)
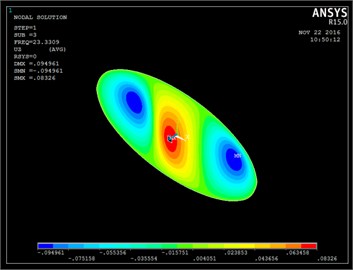
e) Modeshape 3 (ANSYS)
f) Modeshape 3 (MATLAB)
By observing the analytical results obtained from the ICCM and results from a commercial software package, ANSYS it is clear that both the results are in good agreement with a considerable error hence ICCM gave a good convergence in the analysis of free vibration of elliptical plate with a rectangular cut-out.
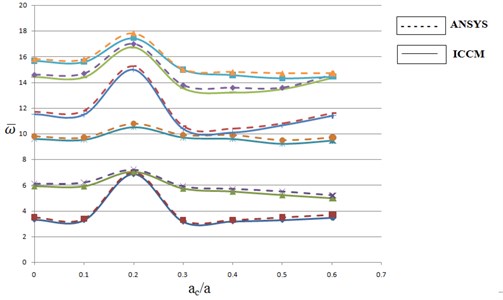
The same procedure is applied for a square hole by increasing its size, while keeping all the remaining parameters are constant, to observe the effect of hole size on the frequency of vibrating structure. The results obtained in this process were plotted in graph (non-dimensional frequency vs size of the hole) for the reader convenience as follows.
Fig. 7First five natural frequencies of SSSS elliptical plate with a concentric square hole
5. Conclusions
The free vibration analysis of an elliptical plate has been investigated to obtain the results with a stable convergence. The obtained results were validated with the available literature and tabulated in the Table 1. The Transformation of global axes of plate domain to the local axes of hole domain using deflection matching condition and deriving the kinetic and potential energies of hole in a closed form expression, considering it as a virtual free edge plate so that the energies of any shaped hole can be easily subtracted from the total energy of the plate, is described by the authors which is known as Independent coordinate coupling method.
An elliptical plate with an aspect ratio equal to 0.5 having a rectangular hole of size 0.2×0.1 at the center of a plate is considered and analyzed under the simply supported boundary condition with 0.3. The comparison of theoretical ICCM values with a commercial ANSYS software in the Table 2, reveals that the results are in good agreement with a negligible error, and states that ICCM is a valid tool in the analysis of elliptical plate with a rectangular hole.
The variation of natural frequency of an elliptical plate with the change in position of cut-out along the axis of symmetry and along a radial line is presented in Fig. 5 and the values are tabulated in Table 3 and Table 4 respectively. From the Fig. 5 it can be clearly observed that as the position of hole is moving towards the center of plate, the fundamental natural frequency value is decreasing either in the variation of position of hole along the axis of symmetry or in the variation of position of hole along a radial line. The reason behind this phenomenon is, having more stiffness at the circumference of plate due to the applied boundary conditions than the stiffness at the center of the plate, with a constant mass.
To study the effect of size of cut-out on the natural frequency of an elliptical plate, a plate with Central Square cut-out of various sizes are assumed and analyzed. The results are plotted in the Fig. 7 which concludes that the increase in size of the hole will lead to increase in the frequency of the plate, in the range of and then decreases in the range of
Hence it is clear that the position and size of hole is having a significant effect on the fundamental natural frequency of the plate. And as the Plate geometry is symmetric about the axes it is also noticed that the same values are obtaining on the other side of the symmetric axis of the plate.
References
-
Prasad K. L., Venkateswar Rao A., Nageswara Rao B. Free vibration of simply supported and clamped elliptical plates. Journal of Sound and Vibration, Vol. 158, 1992, p. 383-386.
-
Leissa A. W. Vibration of a simply supported elliptical plate. Journal of Sound and Vibration, Vol. 6, 1967, p. 145-148.
-
Maurizi M. J., Belles P., Laura P. A. A. Free vibration of clamped elliptical plates. Journal of Sound and Vibration, Vol. 171, Issue 1, 1994, p. 141-144.
-
Lam K. Y., Liew K. M., Chow S. T. Use of two-dimensional orthogonal polynomials for vibration analysis of circular and elliptical plate. Journal of Sound and Vibration. Vol. 154, Issue 2, 1992, p. 261-269.
-
Shibaoka Y. On the transverse vibration of an elliptic plate with clamped edge. Journal of the Physical Society of Japan, Vol. 11, Issue 7, 1956, p. 797-803.
-
Mcnitt R. P. Free vibration of damped elliptical plate. Journal of Aerospace Science, Vol. 29, Issue 9, 1962, p. 1124-1125.
-
Waller Mary D. Vibrations of free elliptical plates. Proceedings of the Physical Society. Section B, Vol. 63, 1950, p. 451-1950.
-
Kwak Moon K., Han Sangbo Free vibration analysis of rectangular plate with a hole by means of Independent coordinate coupling method. Journal of Sound and Vibration, Vol. 306, 2007, p. 12-30.
-
Torabi K., Azadi A. R. Vibration analysis for rectangular plate having a circular central hole with point support by Rayleigh-Ritz method. Journal of Solid Mechanics, Vol. 6, Issue 1, 2014, p. 28-42.
-
Paramasivam P. Free vibration of square plates with square opening. Journal of Sound and Vibration, Vol. 30, 1973, p. 173-178.
-
Hegarty R. F., Ariman T. Elasto-dynamic analysis of rectangular plates with circular holes. International Journal of Solids and Structures, Vol. 11, 1975, p. 895-906.
-
Aksu G., Ali R. Determination of dynamic characteristics of rectangular plates with cut-outs using a finite difference formulation. Journal of Sound and Vibration, Vol. 44, 1976, p. 147-158.
-
Rajamani A., Prabhakaran R. Dynamic response of composite plates with cut-outs. Part I: Simply-supported plates. Journal of Sound and Vibration, Vol. 54, 1977, p. 549-564.
-
Rajamani A., Prabhakaran R. Dynamic response of composite plates with cut-outs. Part II: Clamped-clamped plates. Journal of Sound and Vibration Vol. 54, 1977, p. 565-576.
-
Eastep F. E., Hemmig F. G. Estimation of fundamental frequency of non-circular plates with free, circular cutouts. Journal of Sound and Vibration, Vol. 56, Issue 2, 1978, p. 155-165.
-
Chakraverty S. Vibration of Plates. CRC Press Taylor and Francis Group, 2008.
