Performance-based plastic design method of high-rise steel frames

1. Introduction

The steel moment frames designed according to the current codes will be subjected to an inelastic deformation under major earthquakes. However, the current seismic design code is generally based on the elastic behavior and considers the inelastic behavior indirectly. In the current China’s seismic design code, it is a practice to calculate the design base shear and elastic drift from code-specified elastic acceleration response spectrum during the minor earthquake, then design members for different combinations of internal forces, and check the elastic drift. The inelastic drift under major earthquakes is estimated as the elastic drift multiplied by a drift amplification factor and should not be beyond the specified limits. To ensure the expected ductility demands and energy dissipation capacity, some appropriate detailing measures should be taken. When hit by the strong earthquakes, however, the structures designed by the above methods will suffer inelastic deformations, which is very difficult to predict and control [1-9]. The inelastic behavior may include severe yielding and buckling of structural members and connections. These inelastic behaviors may be unevenly distributed in the structure, which may lead to a rather unfavorable response, sometimes even total collapse, or laborious and expensive repair work [10-12].

In recent years, it is found that quite a few strong earthquakes have led to great loss of life and property. The strength-based seismic design method cannot satisfy the requirements, and furthermore the performance-based seismic design (PBSD) method has been in the limelight. The performance-based seismic design philosophy has emerged as a promising and efficient seismic design approach. PBSD explicitly accounts for the inelastic behavior of a structural system in the design process itself [13-17]. However, the PBSD method depends primarily on an iteration process, namely, “Evaluate performance”, “Modify design”, “Evaluate performance” until the designed structure can reach the desired performance [10-12]. A recently developed performance-based plastic design (PBPD) methodology is considered in the present study in which inelastic characteristics of structural components are directly considered in the design [18, 19]. This design methodology has already been successfully applied to various structural systems [10, 20-25]. This study presents an application of PBPD method to high-rise steel moment frames. A steel moment resisting frame has been designed using the PBPD method in accordance with GB50011-2010 Code [1]. In this method, the target drift and yield mechanisms are pre-selected as key performance criteria. The design base shear in a given earthquake level is calculated based on the work-energy balance principle that the work required to push the structure monotonically to the target drift is equal to the energy needed by an equivalent single degree of freedom to reach the same state. The plastic design is utilized to design the frame members and connections so as to attain the desired yield mechanism and behavior. The PBPD method can account for the inelastic structural behavior directly without any evaluation and iteration. The concept of the PBPD method is very clear and the design process is simple, which can enjoy a wide engineering application.

2. PBPD method

The PBPD method employs pre-selected target drift and yield mechanisms as performance limit states. These two limit states are directly dependent on the degree and distribution of structural damages, respectively. The design base shear for a specified earthquake level, is calculated based on the work-energy balance principle that the work required to push the structure monotonically to the target drift is equal to the energy needed by an equivalent EP-SDOF to reach the same state (Fig. 1). Then the plastic design is utilized to design the frame members and connections so as to attain the desired yield mechanism and behavior.

Fig. 1PBPD concept

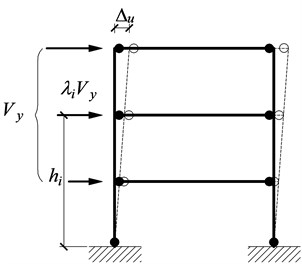
a) Yield mechanism

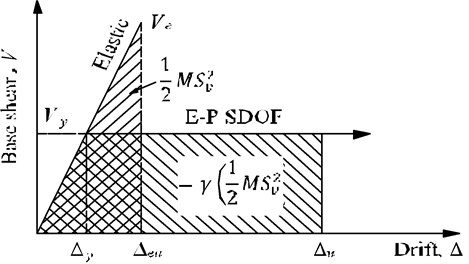
b) Energy-work balance concept

2.3. Member design in steel frames

2.3.1. Design of beams (designated yielding members)

During the major earthquakes, in order to avoid structural collapse, dissipate the input energy maximally, and ensure the sufficient strength and ductility of structure, it is necessary to select a reasonable yield mechanism at the beginning of design. When the target yield mechanism shown in Fig. 2 is adopted for steel moment frames, it is natural that the beams become the primary designated yielding members (DYM). The required moment capacity of beams at each story can be yielded by the plastic design approach and referring to Fig. 2:

17

$\sum _{i=1}^n{F}_i{h}_i{\theta }_p=2M_{pc}{\theta }_p+\sum _{i=1}^{n}2M_{pbri}{\gamma }_i,$

where $M_{pbri}$ is the required moment strengths of beams at story $i$. The rotation term ${\gamma }_i=\left(L/{L\text{'}}_i\right){\theta }_p$ (Fig. 2). Note that the external work done by the uniform gravity load is zero since the beams experience the antisymmetric deformations.

The relevant research results have indicated that the desirable distribution of structural strength along the building height should correspond to the distribution of the design story shears. This contributes to the more uniform distribution of the yielding along the height, thus to avoid the concentrated yielding at a few stories. That is:

18

$M_{pbri}={\beta }_i{M}_{pbr},$

where $M_{pbr}$ is the required plastic moment of beams at the top story.

Fig. 2Target yield mechanism for moment frames

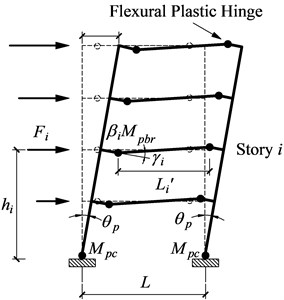
Fig. 3Single span moment frame with a soft story

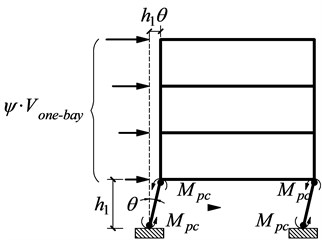
During the earthquake, in order to prevent the soft story mechanism occurring in the first story (shown in Fig. 3), the required plastic moment of columns should be reasonably determined. Assuming that plastic hinges arise at both ends of the first story columns, for a small deformation $\theta$, the corresponding work equationis [26]:

19

$\mathrm{\Psi }{V}^{\text{'}}{h}_1\theta =4M_{pc}\theta ,$

then:

20

$M_{pc}=\frac{\mathrm{\Psi }V\text{'}{h}_1}{4},$

where, $\theta$ is a small mechanism deformation, $V\text{'}$ is the base shear (for an equivalent one bay model), which may be taken as $V$ divided by the number of bays; $h_1$ is the height of the first story; the factor $\mathrm{\Psi }$ accounts for over strength above the design force. This method was used in the design example with a value of 1.1 for the over strength factor $\mathrm{\Psi }$.

Substituting Eqs. (20) and (18) into Eq. (17), the required plastic moment ${\beta }_i{M}_{pbr}$ of beams at story $i$ can be obtained.

The steel beams can be designed according to flexural members, and the cross section of the beam at story $i$ should satisfy the following:

21

$M_{pbi}=W_{ni}f\ge {\beta }_i{M}_{pbr},$

where, $M_{pbi}$ is the design plastic moment of beams at story $i$, $W_{ni}$ is the plastic net section modulus of beams.

2.4. Design of columns (non-DYM)

Columns are non-designated yielding members (non-DYM) and they must have enough strength to resist the unfavorable combinations of factored gravity loads and maximum expected strength of the DYM simultaneously by involving the consideration of reasonable strain-hardening and over strength of materials. In the design of moment frames, the steel columns can be separated as cantilever free bodies. The free-body diagram of an exterior column at the target drift is shown in Fig. 4.

Fig. 4Free-body diagram of an exterior column

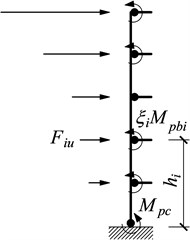
In order to guarantee that the intended strong column-weak beam mechanism will accrue to the structure; the designed columns must resist the maximum expected forces by considering a reasonable extent of strain-hardening and material over strength in the beam plastic hinges. The moment of plastic hinge at a strain-hardened beam can be determined by multiplying the required moment strengths $M_{pbri}$ by an appropriate overstrength factor $\xi$, which should account for the effect of strain-hardening and material over strength. Assuming the distribution of the required lateral forces $F_{iu}$ acting on this free body may follow the distribution as given by Eq. (16), the magnitudes of $F_{iu}$ can be readily obtained by the equilibrium conditions of the free body. Then the moments and shear force of column at each story can be computed by the use of the beam end moments and lateral forces applied at each story $F_{iu}$.

In the case of steel moment frames, the sum of required counterbalance lateral forces, $F_L$, acted on the free body of an exterior column can be obtained as Fig. 5(a):

22

$F_L=\frac{\sum _{i=1}^n{\left(M_{pr}\right)}_i+\sum _{i=1}^n{\left(V_{sw}\right)}_i\cdot {\left(w+\frac{d_c}{2}\right)}_i+M_{pc}}{\sum _{i=1}^n{\alpha }_i{h}_i},$

where $w$ is the width of shear plate and:

23

${\alpha }_i=\frac{\left({\beta }_i-{\beta }_{i+1}\right)}{\sum _{i=1}^n\left({\beta }_i-{\beta }_{i+1}\right)},i=n,{\beta }_{n+1}=0.$

Eq. (22) neglects the gravity load on the short length of the beam between the plastic hinge and the face of the column.

For the case of interior column tree, both directions of lateral forces lead to the same result; hence only the lateral forces acting to the left are shown in Fig. 5(b).

The sum of lateral forces, $F_L$, can be calculated as:

24

$F_L=\frac{2\cdot \sum _{i=1}^n{\left(M_{pr}\right)}_i+{\sum }_{i=1}^n\left[{\left(V_{sw}\right)}_i+{\left(V_{sw}^{\text{'}}\right)}_i\right]\cdot {\left(w+\frac{d_c}{2}\right)}_i+2M_{pc}}{\sum _{i=1}^n{\alpha }_i{h}_i}.$

Fig. 5Free-body diagram of a column tree

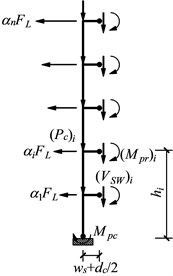
a) Free-body diagram of an exterior column tree (lateral forces acting to the left)

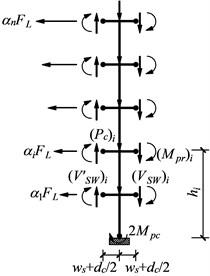
b) Free-body diagram of an interior column tree (lateral forces acting to the left)

3. PBPD procedure

(1) For the design earthquake level, select a desired yield mechanism and target drift ${\theta }_u$ for the structure consistent with the intended performance objectives. Assume idealized elastic-plastic (EP) force-displacement behavior and estimate yield drift ratio, ${\theta }_y$, for the structure.

(2) Compute the plastic drift ratio ${\theta }_p$ by deducting the yield drift ratio ${\theta }_y$ from the pre-selected target drift ratio ${\theta }_u$.

(3) Estimate fundamental period $T$ for the system from the mass and stiffness properties. Empirical formulae based on codes (e.g. GB50009-2012) can also be used to estimate the expected fundamental period of the system. Use an appropriate vertical distribution of design lateral forces.

(4) With the information in Steps 1 and 2, along with the design spectral acceleration value, $S_a$, calculate the design base shear, $V$, by the work-energy balance principle that the work required to push the structure monotonically to the target drift is equal to the energy needed by an equivalent single degree of freedom to reach the same drift. At this time, a rational theory of inelastic seismic response spectrum for EP-SDOF can be employed, such as idealized inelastic response spectra proposed by Newmark-Hall or other methods.

(5) If the force-deformation behavior of the structure is different from the assumed elasto-plastic behavior, then design base shear $V$ should be modified.

(6) Use the plastic method to design the beams (Designated Yielding Members, DYM), while having the distribution of lateral strength of the structure along the height follow the distribution of design story shear. Columns required to remain elastic (non-DYM), are designed by a capacity design approach, by accounting for the strain-hardening and material over strength of the DYM as well as by including the $P-\mathrm{\Delta }$ effects due to the frame deformation.

4. Case study

4.1. Project overview

The project is a ten-story steel frame with the story height of 3.6 m. The floor and roof dead loads are 4.5 kN/m², the floor live load is 2.0 kN/m², the roof live load is 0.5 kN/m², and the snow load is 0.3 kN/m². The seismic fortification intensity is 8°. The site condition is type Ⅱ. The design earthquake classification is the 1st group. The framing plan and elevation of the moment frame are shown in Figs. 6-7, respectively.

Fig. 6Floor plan of structure

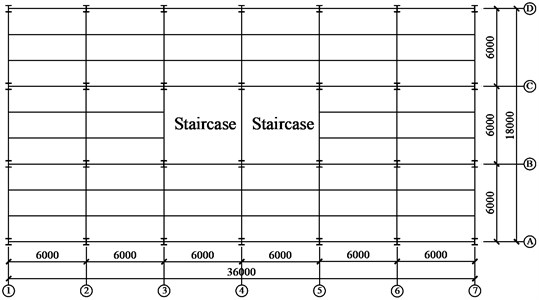
Fig. 7Elevation view of structure

Table 1Member sections

Floor	Beam section	Exterior column section	Interior column section
10	H450×220×8×10	H400×400×12×16	H400×400×12×16
9	H450×220×8×10	H400×400×12×16	H400×400×12×16
8	H450×220×8×10	H400×400×12×16	H400×400×12×16
7	H450×220×8×10	H400×400×12×16	H400×400×12×16
6	H450×220×8×10	H400×400×12×16	H400×400×12×16
5	H500×200×8×10	H450×450×15×20	H450×450×15×20
4	H500×200×8×10	H450×450×15×20	H450×450×15×20
3	H500×200×8×10	H450×450×15×20	H450×450×15×20
2	H500×200×10×16	H500×500×15×20	H500×500×15×20
1	H500×200×10×16	H500×500×15×20	H500×500×15×20

The welded H-shaped sections are selected for both beams and columns and the steel is Q235-B.F. The preliminary member sections are show in Table 1.

5. Verification by nonlinear analysis

Nonlinear dynamic time-history analyses were carried out by using the finite element software SAP2000 so as to verify the above calculation results. The hinge P-M3 is used to simulate the material nonlinearity of the frame columns, and the hinge M3 to simulate the nonlinearity of the frame beams. The mechanical behavior of plastic hinges can be determined in accordance with FEMA-356 [28]. The peak of the earthquake accelerogram in the time history analysis is determined by the current code [1]. The selected earthquake waves are respectively Lanzhou wave 1, Artificial wave 2, Artificial wave 3, Elcentro, Cape Mendocino, Taft, Chichi, Coalinga, Loma and Landers as shown in Table 8. These ten waves vary in their frequency contents. Figs. 8-9 illustrate the maximum interstory drift ratios of the PBPD frame from time-history analyses using appropriately scaled ground motion records representative of moderate earthquake and major earthquake.

Fig. 8Maximum interstory drift ratios of PBPD frame under moderate earthquake

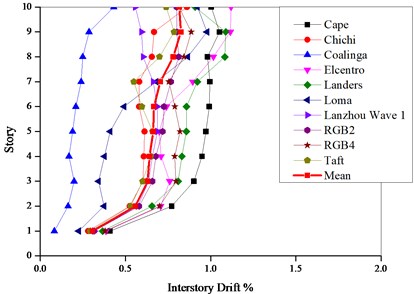
Fig. 9Maximum interstory drift ratios under major earthquake

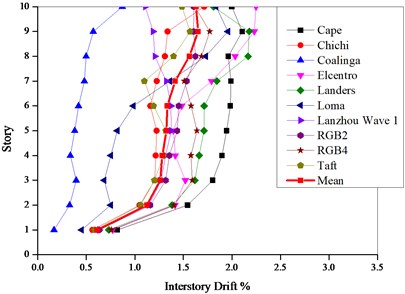
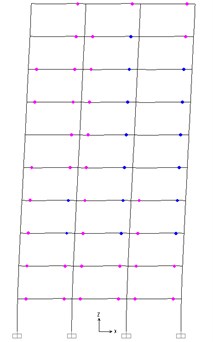
Fig. 10Plastic hinge distribution of PBPD frame

From Figs. 8-9, the maximum interstory drift ratios are comparatively uniform along the height of structure (except the first story) under all the seismic waves except Elcentro and Loma wave. The means of the interstory drift ratio respectively follows within 0.56 %-0.81 % and 1.12 %-1.6 % under the moderate and major earthquakes, which indicates that the inelastic activity is more evenly distributed over the height and the seismic energy can be dissipated simultaneously by each floor. Unlike the traditional design method, the seismic energy can be dissipated only by one story or several soft stories. The results indicate that the mean maximum interstory drifts of the PBPD frame are well less than the corresponding target values.

The plastic hinge distribution under the major earthquake is shown in Fig. 10. It can be indicated from Fig. 10 that the plastic hinges form on either end of each beam meeting the desired yield mechanism. However, the plastic hinges do not form on the column bases due to the conservative design of the first story.

6. Pushover analysis

Aiming at the steel frames designed according to the current code and PBPD method, Pushover analyses are performed on these two frames by SAP2000. Adopt the inverted triangular distribution of lateral force, respectively push the structures to the top displacement of 720 mm and 1080 mm, and the interstory drift of each story is shown in Figs. 11-12.

As shown in Figs. 11-12, compared to the traditional steel frames, the PBPD frames present the more evenly distributed interstory drift, which indicates that the inelastic activity of PBPD frames is more uniformly distributed along the height of structure than the traditional frames and the PBPD frames display the more desirable seismic performance.

Fig. 11Drift ratio under Pushover at 2 % roof drift

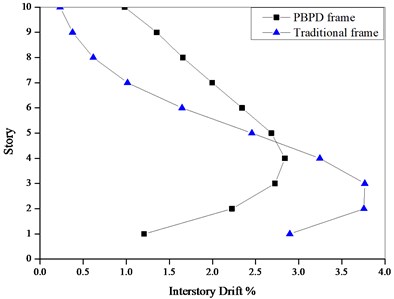
Fig. 12Drift ratio under Pushover at 3 % roof drift

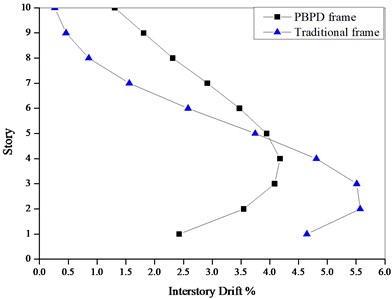
Fig. 13Plastic hinges under pushover at 4 % roof drift

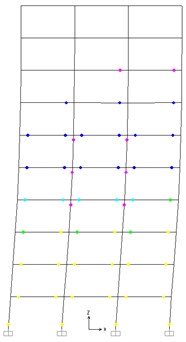
a) Traditional frame

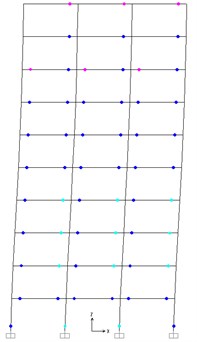
b) PBPD frame

Fig. 13 shows the distribution of plastic hinges of the traditional frames and PBPD frame when these two frames are pushed up to 4 % roof drift. From Fig. 13, for PBPD frames, the plastic hinges desirably appear at both ends of the beams, and no unintended plastic hinges occur in the columns. For the traditional frames, the plastic hinges form in the beams of each story, but there are also plastic hinges in the columns of the 1st story and 4-6 stories. Fig. 13 demonstrates that the deformation distribution of plastic hinges in the PBPD frames is more uniform along the height than those of the traditional frames, which demonstrates that the PBPD frame exhibit an excellent seismic performance.

7. Conclusions

1) The PBPD method uses predetermined target drift and yield mechanisms as important performance objectives. During the design process, the PBPD method can introduce structural nonlinear behavior directly and key performance criteria. Accordingly, the utilization of the PBPD method in the design of high-rise steel frames can eliminate the need for any assessment or iteration after initial design.

2) Through the comparison of seismic performances between the PBPD frame and traditional frame assessed by the nonlinear static analysis and dynamic time history analysis, the validity and reliability of the PBPD design method is demonstrated. In contrast to the traditional frame, the inelastic activity of the PBPD frame along the building height tends to more evenly distributed, which means that the PBPD frame exhibit an excellent seismic performance.

3) The method in this paper can be used to design the steel frame under different performance levels and to control the performance of the steel frame under frequent intensity, basic intensity, and infrequent intensity of the earthquakes.