Dynamic response analysis of intake tower in hydroelectric power station with high surrounding rock

2.1. Viscoelastic artificial boundary theory

Viscoelastic artificial boundary absorbs the energy of scattered waves which spread from the upper by adding spring-damper unit on truncated boundary node, at the same time it reflects the resilience of the elastic medium. The acceleration and displacement are transformed into the equivalent nodal force on the artificial boundary; its Eq. (1) is:

where $P_b^f$ denote the equivalent nodal forces acting on the artificial boundary node, $\left[{\mathbf{K}}_b\right]$, $\left[{\mathbf{C}}_b\right]$ are the stiffness matrix and the damping matrix, and $\left\{{\mathbf{u}}_b^f\right\}$, $\left\{{\dot{\mathbf{u}}}_b^f\right\}$ are the free field displacement and velocity vectors.

The node damping coefficient $C$ and the spring stiffness coefficient $K$ of viscoelastic artificial boundary can be calculated as follows [19]:

Normal boundary:

Tangential boundary:

where $\rho$, $G$ is denote the density and the shear modulus of the medium; $c_s$and $c_p$are the propagation velocity of shear wave and compression wave in the medium. $r$ is the distance from the artificial boundary node to the scattering source; ${\alpha }_N$ and ${\alpha }_T$ are the normal and tangential stiffness correction coefficient.

2.2. The frequency domain inversion of seismic for bedrock motion

The seismic acceleration of bedrock is different from that of the free field [20]. As known ground acceleration time history, the seismic acceleration can be obtained from the frequency-domain inversion.

In the layered field, the inversion of the ground motion time history to the bedrock is carried out based on the theory of transient seismic response of linear hysteresis layer. The process is generally as follows: After read, the earthquake acceleration transform the transient waves into steady wave by using Dispersed Fourier Transform, the Fourier spectra of the composite is obtained by calculating the steady wave of the deep strata, by using the inverse Fourier Transform the time history of ground motion then obtained [21].

2.3. Type L terrain seismic input

The height of the free field surface of pre-and post the bank-tower intake composites a L-shape topography, the same height of the free surface seismic motion input was unreasonable [22-24]. The viscoelastic boundary should be study deeply for this situation.

First, a numerical experiment is made to validate the viscoelastic artificial boundary program. Some principles of displacement time history curves are getting to infer whether the proposed method is correct.

Two finite-element models were established (Fig. 1). Model A size: 100 m×100 m×50 m (length, width, height); model B size: 100 m×100 m×100 m (length, width, height). Spring-damper units were set at the bottom face and the four sides, then three directions stiffness coefficient and damping coefficient were calculated to complete the viscoelastic artificial boundary. Consider the wave propagation effects, the displacement and velocity time history of each node were generated by program, then the equivalent load on the node can be computed.

Fig. 1The 50 m and 100 m height finite element model and monitoring points

a) Model A

b) Model B

c) Schematic diagram of monitoring points

Material parameters, velocity and displacement inputs are referred in literature [25]. Material properties are defined as follows: elastic modulus = 24 MPa, Poisson’s ratio = 0.2 and density = 1000 kg/m³.So, shear wave velocity $c_s=$ 100 m/s, shear modulus $G=$ 10 MPa, compression wave velocity $c_p=$ 163.3 m/s. The material damping coefficient is zero, and the expressions of displacement $u\left(t\right)$ and velocity function $\dot{u}\left(t\right)$ are as follows:

In order to observe the displacement of every moment setting up three monitoring points at the bottom, middle and top of the model’s center line as shown in Fig. 1. The input wave transmitted in sequence at different depth points in the medium, when the peak value of the displacement wave spreads to the ground surface, the value of incident and reflected waves were superposed, the maximum displacement value is two times the peak value of the incident wave.

The displacement time history curve at three monitoring points Fig. 1(c) of models are shown in Fig. 2. From the figure, the peak value and the propagation curve shape of the wave obtained by numeric solution Fig. 2(b) and Fig. 2(d) are close to the theoretical solution Fig. 2(a) and Fig. 2(c), which proves the correctness of the viscoelastic artificial boundary program.

Establish a typical L-shape model, its size as shown in Fig. 3(a), and the location of each monitoring point marked in the intermediate profile as shown in Fig. 3(b). Part the vertical stepped terrain model into pre-and post-two parts as shown in Fig. 4, equivalent load time history of each layer was calculated that the pre-and post of upper free surface as the reflection face.

Fig. 2The horizontal displacement of monitoring points

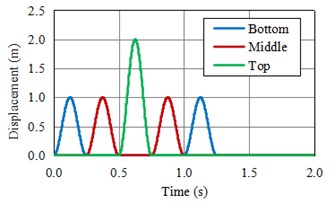
a) Theoretical solution of horizontal displacement of monitoring points in model A

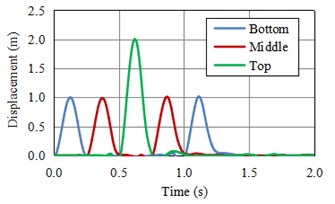
b) Numerical solution of horizontal displacement of monitoring points in model A

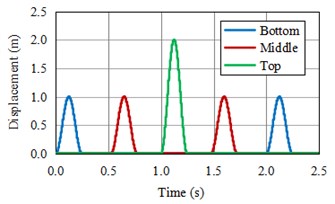
c) Theoretical solution of horizontal displacement of monitoring points in model B

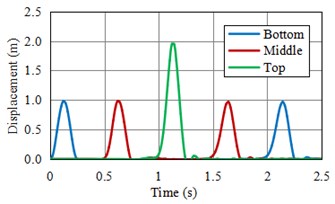
d) Numerical solution of horizontal displacement of monitoring points for model B

Fig. 3L-shape finite element model and monitor points

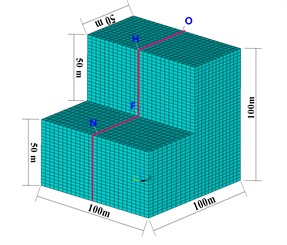
a) The diagram of 3D finite-element model size and observation point

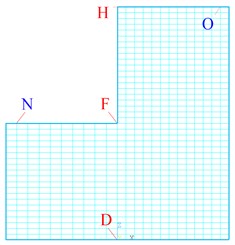
b) The diagram of intermediate profile of model and monitoring points

The horizontal displacement of the monitor points N and O of L-shape model as shown in Fig. 5(a). These two points are close to the left and right sides, the peak value of two monitor points’ displacement about 2 meters, its consistent with the theoretical value and all appear in the moment of conformity with the theoretical time (With the reference to Fig. 2(a) and Fig. 2(c), respectively), it presents that the loading method of viscoelastic artificial boundary for step topography is feasible. At the same time, from the displacement curve, it shows that the points N and O still have positive or negative displacement after the wave propagation over at about 1.25 s, these are different from the situation of model A or B, it can be inferred that wave will engender unbalanced force to result displacement when wave propagate in the medium with height difference.

The horizontal displacement curve of three nodes from bottom to top at the height mutation position of model midplane are shown in Fig. 5(b), the curve shape and peak value of these three nodes’ displacement time history are totally different from model A or B, the peak value of monitor point H at the surface top appears a little later than the point O at the same height , and the value larger than the superposition value 2 meters of incident and reflection, this shows the volley face has a special amplification effect, and there has a larger negative displacement before the wave propagates to the point H; The peak displacement value of point F less than the point N’s value 2 meters, but greater than input displacement peak value 1 meter, and half the value of point H. This is due to the model before and after the application of the load imbalance has produced additional torque. The peak value of each monitor point has good proof to literature [8]. It shows reasonable methodology.

Fig. 4The calculate partition plan of vertical step model

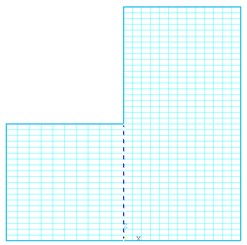
Fig. 5Numerical solution of displacement time history of observation point of step model

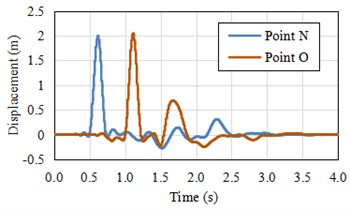
a) The horizontal displacements of point N and O on model free face

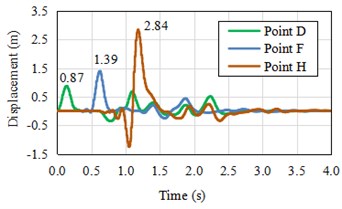
b) The horizontal displacements of the nodes from bottom to top at the middle line of model

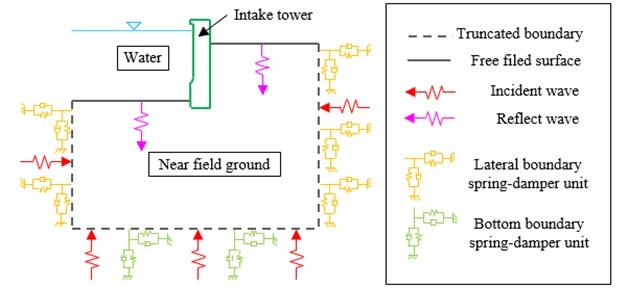
Based on analysis and verification above, establishment the viscoelastic artificial boundaries system of the intake tower is shown in Fig. 6.

Fig. 6The schematic diagram of viscous artificial boundary system of intake tower

3.1. The basic parameters of intake tower

Based on the spillway tunnel intake tower of a real hydropower project, the elevation of base plate of the intake tower is 1635.00 m, the thickness of bottom plate is 5.0 m, the top elevation of inlet is 1716.00 m, and height of the inlet is 86 m. The normal water level is 1710.00 m. There are 35 meters backfill beside and behind the tower and connect with surrounding mountain. The level for seismic design of water release structure is exceeding probability of 5 % in 50 years; the peak motion acceleration value is 201.0 gal. The corresponding seismic fortification intensity is VIII. Engineering material parameters are provided in Table 1 and Table 2.

3.2. The finite element model and load condition

The model with finite-element software and use space Cartesian coordinate system, setting the coordinates origin in the center of the front side of inlet height of base plate of the intake tower, the $X$ axis pointing along the direction of flow; the $Y$ axis is perpendicular to the direction of flow; the $Z$ axis along the height direction of the tower. The depth of foundation is one time the height of the tower, the upstream and downstream foundation size is 50 m, the left and right sides are the same. Three-dimensional solid element is adopted for the tower and the foundation rock, and the inertia effect of the water on the tower is reflected by the addition mass element [1].

Tower-foundation finite element model as shown in Fig. 7.

There are five cases calculated to compare which listed in Table 3.

Fig. 7The tower-foundation finite element model

a) The whole model

b) The intake tower

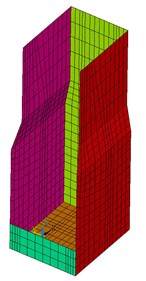
c) The contact element area

For model 2 and 4, the flexible-to-flexible body surface-to-surface 3D contact element are set between the tower and the surrounding mountain so that can simulate the state like crack or slip or contact between tower and rock during an earthquake Fig. 7(c). For face-to-face contact element, the improved Lagrange algorithm was used.

The seismic response spectrum given by the geological survey as the target spectrum to generate horizontal and vertical acceleration of earthquake wave, the fitting response spectrum and the target spectrum error are less than 5 %, and the acceleration baseline correction is carried out.

Fig. 8The artificial fitted acceleration time history

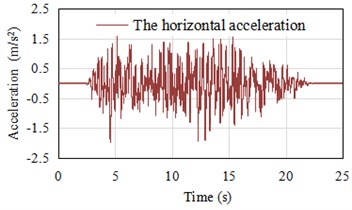
a) Horizontal acceleration time history PGA = 1.973 m/s²

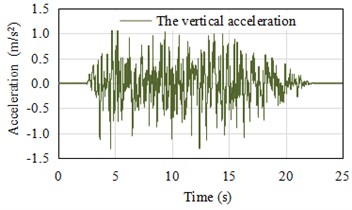
b) Vertical acceleration time history PGA = 1.315 m/s²

Fig. 9The retrieved acceleration time history (Horizontal direction PGA = 1.756 m/s2)

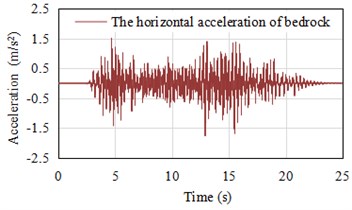
Three direction accelerations are directly put on massless foundation model 1 and 2 during a seismic time-history response; the model 3 to 5 used the viscoelastic boundary, the acceleration time history of the bedrock was inversion from the ground. After the acceleration adjusted and filtered, the displacement and velocity are obtained by integration, and the equivalent load on each node is obtained by using the program based on wave theory.

4.1. The displacement of intake tower

Deformation of the intake tower is an important refer in seismic response. Three directions’ displacement of the five intake tower models listed in Table 4.

As can be clearly seen from Table 4, except the displacement along river flow direction of model 1, the maximum displacement values of the viscoelastic artificial boundary model (Model 3 to 5) are generally lower than the massless foundation models (Model 1 and 2), especially in the cross-flow direction the maximum reduced up to 80 %. The maximum displacement value of each direction occurrences slightly delayed than the input acceleration peak time of models without contact, and the peak value appearance time of contact models is not necessarily near the time of the input acceleration, the contact models’ displacement generally greater than the models without contact. This is because of the intake tower and the surrounding rock and foundation are a whole, the deformation of the intake tower restricted by surround rock, but the models with contact intake tower and surrounding rock may disengage during an earthquake, the deformation range of the tower body becomes larger which is closer to the fact that the intake tower and the backfill are not fully consolidated.

Model 5 set the viscoelastic boundary, but the free surface before the tower as the reflective face for wave propagation. It can be seen that the displacement value is greater than the model 3 or 4 that also using viscoelastic boundary, but it is little less than the model of massless foundation. The results show that the model 5 can be a certain extent embodies of the effects of radiation damping of infinite foundation, and the result is better than massless foundation method.

4.2. The stress of intake tower

Maximum principal stress and occurred moment of the intake tower of five models are listed in Table 5.

Seen from the Table 5 and Fig. 10, the maximum value of the stress located in the connection parts of the tower and the surrounding rock, the material is not considered nonlinear so that the value of the resulting stress is larger. The results of the five models are compared: The absolute maximum value of the model of the massless foundation is larger than that of the model 3 and model 4. The stress value of the contact model is obviously smaller than that of the model without contact. Model 4’s maximum value of the first principal stress decreased by nearly 57 % than model 1’s, it proves that the model used viscoelastic boundary with contact can effectively weaken the reflection of energy in the foundation, and the stress can release at the tower and the surrounding rock connect part. The maximum stress occurred at the same time for model 5 and model 3, but stress value of model 5 is greater than other models, so this set of viscoelastic boundaries cannot dissipate energy even increased the structure response. It proves that reasonable selection of viscoelastic boundary reflection faces has significant influence to result.

4.3. The acceleration changes along the height of intake tower

In order to compare the acceleration changes along the height of intake tower under different boundary conditions, model 3 to 5 were selected as the study object. ABCD four measuring points were set to observe the change of acceleration distribution along the height of intake tower, these points’ position was shown in Fig. 11(a). Point A at the top of intake tower, point B is located between point A and point C, point C at the demarcation line between tower and backfill and point D at the bottom of intake tower. Make the coordinate zero point at point D, when the maximum acceleration value of point A was appearing, then get the acceleration results from point B, C and D for model 3 to model 5, the acceleration distribution along the tower was obtained. Fig. 11(b).

Seen from the Fig. 11(b): point D to C, the acceleration value between models have litter alter from point D to C, this is due to the CD segment of the tower close to the back mountain, the acceleration along the height is difficult to amplify. From point C to A, the acceleration of three models are increased in a line tread, and the maximum of acceleration from model 3 to 5 is 7.51 m/s², 5.11 m/s², 11.63 m/s². The viscoelastic boundary is adopted in this paper with contact the smallest increase along the height of the acceleration, and the largest increase in model 5. For three models, the acceleration ratio of point A to C is 15.9, 7.4 and 28.5. The above comparison also shows that the load input method and the contact boundary conditions have significant influence on the results of dynamic analysis of intake tower.

Fig. 10Maximum principal stress of the intake tower

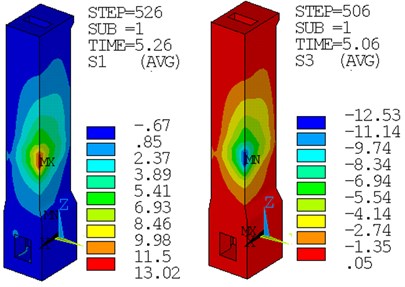
a) The first and third principal stress of model 1, Unit: MPa

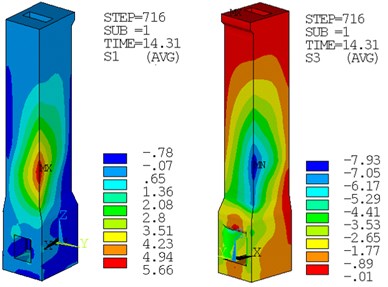
b) The first and third principal stress of model 4, Unit: MPa

Fig. 11Acceleration along the intake tower height distribution

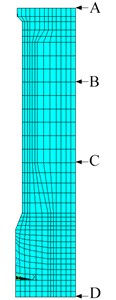
a) Schematic diagram of analysis point

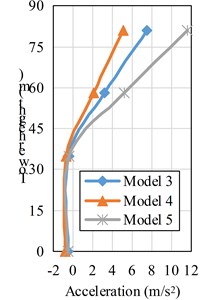
b) Distribution of acceleration along height

4.4. The contact state of intake tower

For model 4, the contact state for the contact area is observed. In the whole process of the earthquake, the bottom of the tower and the foundation has been in a closed state of adhesion.

Some parts of two sides of the intake tower cracked but in contact state during earthquake, crack position changes with time, the initial cracking part is mainly at the two sides of the bottom of the base plate, the cracking range extends from the back of the base plate to the middle-front region; but other parts recovery to adhesion state when cracking Fig. 12(a).

At the time of 14.07 s, the part that two flanks of the intake tower at the body shape contraction rear back is cracked, but the crack does not extend to the lower part or the upper part, these instructions that they still have good consolidation between the tower and the surrounding rock except small parts are cracking and contacting.

The front face has good adhesion between the intake tower and the rock during the earthquake. The behind sides of tower ship or cracking at six moments. Cracking at the highest boundary line of the surrounding rock behind the tower and cracks expand to the lower part over time, the deepest location of the cracking was achieved in 14.31 s Fig. 12(b), the upper contact adhesion state recovery.

Fig. 12Contact status of both sides and rear side of the intake tower

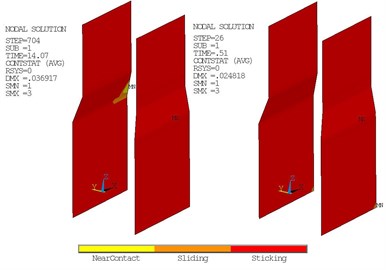
a) The contact states of both sides of the intake tower at 14.07 s and 0.51 s

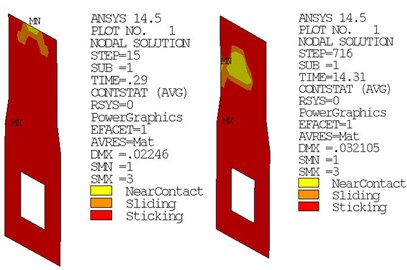
b) The contact states of back of intake tower at 0.29 s and 14.31 s

From the analysis above, in the design earthquake, although around the intake tower have some crack, no penetrative disengage in the model, even after cracked it still in the contact state, and only small range in the cracking position and other cracked locations restores adhesion state at every time, it can be concluded that intake tower without sliding or overturning, its stability meets the request.