Blind source separation of rolling element bearing’ single channel compound fault based on Shift Invariant Sparse Coding

1. Introduction

The rolling element bearing is the most widely used part in the rotating machinery. It is necessary to study the effective fault feature method of rolling element bearing to avoid catastrophic accident due to the failure of it. The Fast Fourier Transform (FFT) and envelope demodulation (ED) were the two traditional and classic methods to extract the fault features of rolling element bearing. However, the above two mentioned methods would not work effectively because the fault vibration signal of rolling element bearing is becoming more and more complex with the increasing complexity of rotating machinery. In recent decades, though several useful techniques such as Spectral kurtosis (SK) [1], Wavelet transform (WT) [2], Minimum entropy deconvolution (MED) [3, 4], Cyclostationary analysis [5, 6] and so on have been proposed for feature extraction of rolling element bearing, most of them are only effective for the single defect of rolling element bearing. Compound fault of rolling element bearing may occur in engineer practice, and now there are only very few effective signal processing based methods to diagnose the compound fault of rolling element bearing. Furthermore, Most of the of the current works on fault diagnosis of compound fault of rolling element bearing are focusing on intelligent algorithms such as Hidden Markov model (HMM), Artificial neural network and so on [7-11] which have the common shortage of time-consuming, so the fault diagnosis of rotating machinery could not be realized timely. So far, several signal processing based methods for fault feature extraction of rotating machinery have been proposed. If localized faults exist in both gear tooth and rolling bearing simultaneously it is difficult to tell the differences between the two types of defects. As such, in paper [12] a new method was proposed to solve the problem by using the meshing resonance and spectral kurtosis algorithm together, and the effectiveness of the proposed method was validated via both simulated and experimental gearboxes vibration signal with compound faults. In paper [13] a hybrid systems named as HGSA-ELM for diagnosis of the compound fault of rolling element bearing was proposed, and the experimental results showed that HGSA-ELM achieved significant high classification accuracy compared with its original version and methods in literatures. A novel method based on the optimal variational mode decomposition and 1.5-dimension envelope spectrum was proposed for detecting the compound fault of rotating machinery [14]. An improved CICA algorithm named constrained independent component analysis based on the energy method was proposed in order to realize single channel compound fault diagnosis of bearings and improve the diagnosis accuracy [15]. To improve the effectiveness of compound fault diagnosis in roller bearings, the paper presented a new method to solve the underdetermined problems and to extract fault features based on variational mode decomposition [16].

SISC [17, 18] is a new signal processing method based on sparse representation, and its application in fault diagnosis of the compound fault of rotating machinery is very limited. In paper [19] a redundant dictionary from a large number of existing signals was trained using SISC and the different bearing faults classification combined with intelligent algorithm was realized. From a different perspective, the basic idea of this paper is to penetrate into the underlying structure of the signal to realize noise cancellation and feature extraction. SISC is used here as the basis function learning algorithm to capture different structural characteristics buried in the signal. By decomposing the original signal simultaneously into these basis functions, fault related time series can be separated through optimal latent component filtering. So, the method proposed in this paper can be considered as a feature enhancing technique without requiring any prior knowledge.

The paper is organized as follows. Section 2 is dedicated to sparse representation and SISC. In Section 3, the processes of SISC in fault diagnosis of the rolling element bearing compound fault are given. Section 4 is the simulation verifying the effectiveness of the proposed method. In Section 5 the experimental analyzed results of rolling element bearing’ three kinds of compound fault (inner race and outer race faults, outer race and rolling element faults, inner race and outer race and rolling element faults) are presented. Conclusions obtained from the above results are given in Section 6.

2. SISC

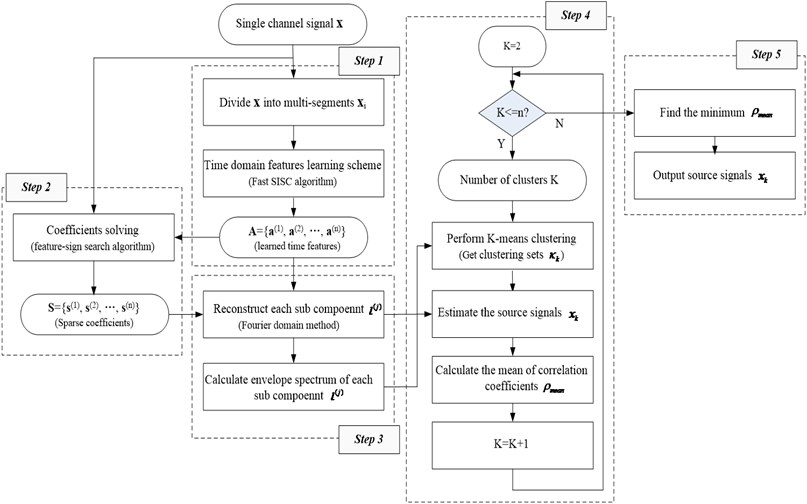
3. The flow chart of the proposed method

As to rolling element bearing fault signal, the feature of damaged races or cage or rolling element of bearings always takes on periodic impulse characteristic. In theory, the different impulses at different damage location can be represented by just one basis function, so SISC is very suitable to analyze the compound fault signal of rolling element bearing. The steps of the proposed method are given as following:

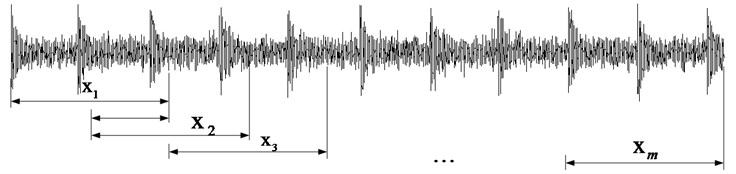
Step1: Divide the one single channel compound observed fault signal $x$ into multi-segments $x_i$ ($i=$ 1,…, $m$) and get the corresponding time-domain feature $a^{\left(j\right)}$ of the observed signal segments $x_i$ ($i=$ 1,…, $m$) and using SISC self-learning algorithm. There are two reasons to segment the signal: 1) Too large training data will cause the SISC dictionary learning algorithm very time-consuming. 2) Each segment is donated as $x_i$ to make sure that at least one fault feature is contained in the segment as shown in Fig. 1.

Fig. 1The segments of the observed signal

Step 2: Fix the time-domain feature $a^{\left(j\right)}$ obtained in Step 1, and the sparse coefficients $s^{\left(j\right)}$ of the observed signal $x$ based on $a^{\left(j\right)}$ are obtained through SISC algorithm presented in Section 2.3.

Step 3: The potential component $l^{\left(j\right)}$ are obtained based on $a^{\left(j\right)}$ and $s^{\left(j\right)}$, and the normalized envelope spectrums of $l^{\left(j\right)}$ are calculated.

Step 4: Vary the clustering number from 2 to $n$, and apply K-mean clustering algorithm to $l^{\left(j\right)}$ and the clustering results ${\kappa }_k$ are obtained. Then the source signal $x_k$ are obtained by regrouping $l^{\left(j\right)}$, and the regrouping equation is shown in Eq. (13). Besides, the mean value of Pearson correlation coefficient ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ (${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ will be discussed in the following content) is also computed to estimate clustering number:

Step 5: Find the minimum ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ obtained in Step 4, and the output signal corresponding to ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ is considered as the last estimated source signal.

The overall flow chart of the above steps is shown in Fig. 2.

Fig. 2The flow chart of the proposed method

In the paper, the optimal clustering number is estimated using the Pearson correlation coefficient ${\rho }_{x,y}$. The Pearson correlation coefficient ${\rho }_{x,y}$ between signal $x$ and signal $y$ can be computed using the following equation:

where ${\mu }_x$ and ${\mu }_y$ represent the mean values of signal $x$ and signal $y$. ${\sigma }_x$ and ${\sigma }_y$ are their corresponding standard deviations. ${\rho }_{x,y}$ is an index measuring the degree of correlation between two variables and its value varies from –1 to 1: 1 represents that the two variables are positively correlated, and 0 represents that the two variables are unrelated completely. It is evident that –1 represents the two variables are correlated negatively. For each clustering number varying from 2 to $n$, the estimated source signal $x_k$ can be reconstructed using Eq. (13). The Pearson correlation coefficient between any two estimated source signals can be calculated using the Eq. (14), and the Pearson correlation coefficient mean value ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ can be obtained. The optimal estimated clustering number can be obtained when the value of ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ is minimum, and the correlation characteristic among the source signals is weakest.

4. Simulation

The fault model of rolling bearing whose mathematical equation can be expressed as Eq. (15) [5, 20] is used to verify the feasibility of the proposed method. ${\tau }_i$ is the tiny fluctuation around mean period $T$. Set the sampling frequency $f_s=$ 2560 Hz, and the shaft rotation frequency is $f_r=$ 10 Hz. The inner race and outer race fault characteristic frequencies are $f_i=$ 105 Hz and $f_o=$ 32 Hz respectively. Assuming the random slide between rolling element and race is normally distributed whose standard deviation is 0.5 % of the shaft rotation ratio:

The outer race and inner race fault source signals and their combined signal are shown in Fig. 3: $a\left(t\right)$ is the outer race fault signal, and $b\left(t\right)$ is the inner race fault signal with $a\left(t\right)+b\left(t\right)$ is their combined signal. According to the processes of the proposed method shown in Fig. 2, the source combined signal is segmented and the data length of each segment is 1024. The overlap ratio is 50 % and the data length of each basis function is 256. The obtained time-domain features $a^{\left(1\right)}$-$a^{\left(8\right)}$ and their corresponding potential components $l^{\left(1\right)}$-$l^{\left(8\right)}$ are shown in Fig. 4. The mean value of Pearson correlation coefficients for each clustering number is shown in Fig. 5. It is evident that the mean value of Pearson correlation coefficient ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ is minimum when clustering number is 2 based on Fig. 5, so the number of source signals is 2. The last re-constructed signal 1 and its envelope demodulation spectrum are shown in Fig. 6(a) and (b) respectively, and the reconstructed signal 2 and its envelope demodulation spectrum are shown in Fig. 6(c) and (d) respectively from which the inner race and outer race fault source signals are separated successfully.

Fig. 3Mixed signal of multi-fault bearing

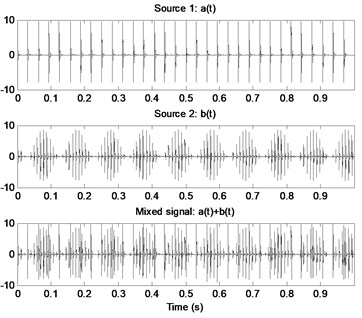
Fig. 4Time features and latent components

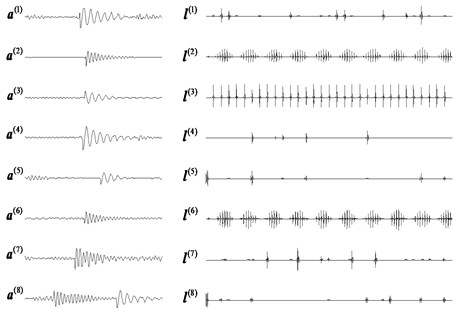
Fig. 5The mean value of correlation coefficients for each clustering number

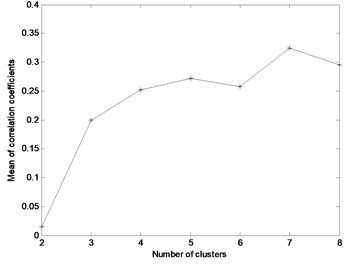
In the above simulation, the noise is not considered, and the white noised is added in the mixed signal shown in Fig. 3 (Mixed signal: $a\left(t\right)+b\left(t\right)$) and the noised mixed signal is shown in Fig. 7. The same steps shown in Fig. 2 are applied on the signal shown in Fig. 7, the obtained eight basis functions are shown in Fig. 8. The mean value of Pearson correlation coefficients for each clustering number is shown in Fig. 9. It is evident that the mean value of Pearson correlation coefficient ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ is minimum when clustering number is 3 based on Fig. 9, so the number of source signals is 3.

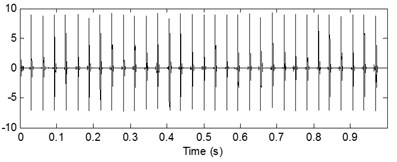
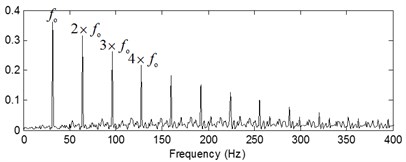
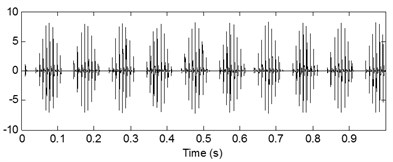
The last analysis results are shown in Fig. 10 and the three source signals are separated successfully.

Fig. 6Recovered sources of simulated signal

a)

b)

c)

d)

Fig. 7Mixed signal with noise

Fig. 88 basis functions

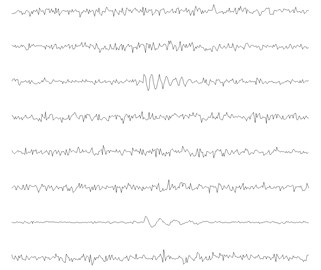
Fig. 9The mean value of correlation coefficients for each clustering number

5. Experiment

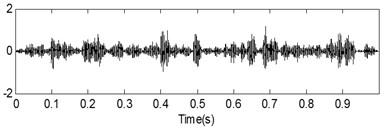
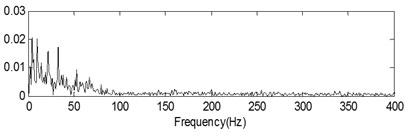
In this section, the application of proposed method in fault feature extraction of rolling element bearing’ experimental compound fault is carried out. The test rig is shown in Fig. 11. The type of test rolling element bearing is NU205 and the relative parameters of the test bearings are given in Table 2. Three types of compound fault are implemented: inner race and outer race compound fault, outer race and rolling element compound fault, inner race and outer race and rolling element compound fault. Process faults on the inner race, outer race and rolling element of the test bearing respectively. The processed faults on inner race, outer race and rolling element of the test bearing are shown in Fig. 12(a), (b) and (c) respectively. The two ends of the shaft are supported by rolling element bearings, and the right end is detachable which is convenient for replacement of the test bearings. The accelerator sensor is added in the vicinity of the test bearings and the peak values of the vibration are collected in the experimental process. The outer race is fixed on the bench and the inner race rotates synchronously with shaft in the test process. The rotating frequency is $f_r=$ 13.3 Hz and the sampling frequency is $f_s=$ 8192 Hz. The characteristic frequencies of inner race fault, outer race fault and rolling element fault are calculated using Eqs. (16)-(18):

In Eq. (16)-(18), $Z$ is the number of rolling elements. $d$ is rolling element diameter. $D$ is the pitch diameter and $\beta$ is the contact angle. The values of $f_i$, $f_o$ and $f_b$ are 95.38 Hz, 64.61 Hz and 5.38 Hz respectively through calculation.

Fig. 10Recovered sources of simulated signal with noise

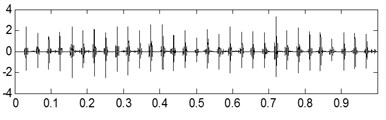
a)

b)

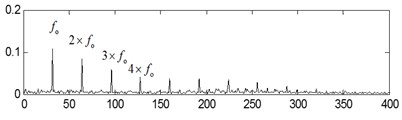
c)

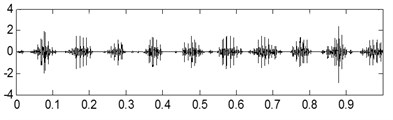
d)

e)

f)

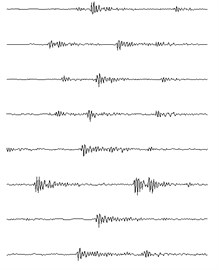
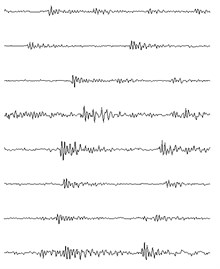
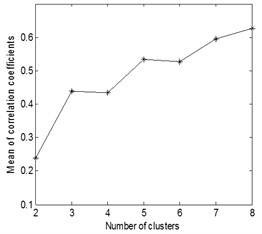
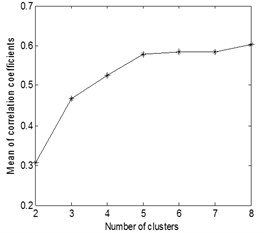
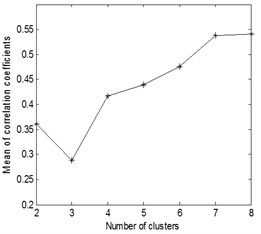
These three kinds of compound fault signals are to be handled using the same process and parameters as in the simulation: The source signals are segmented and the data length of each segment is 1024 point, and the overlap ratio is 50 %. The number and data length of the basis functions are 8 and 256 point respectively. The 8 time-domain feature of the three kinds of compound fault signals are shown in Fig. 13, and the mean value of correlation coefficients ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ for each clustering number of the three kinds of compound fault are shown in Fig. 14: it is evident when the clustering numbers are 2 the ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ of the first and second source signals are minimum, and the clustering number is 3 the ${\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ of the third source signal is minimum. These verify that the fault sources numbers of the three kinds of compound fault signals are estimated correctly.

Fig. 11The test rig

Fig. 12The processed faults on rolling bearing’ inner race, rolling element and outer race

a) Inner race fault

b) Rolling element fault

c) Outer race fault

Fig. 13The 8 basis functions of the three kinds of compound fault

a)

b)

c)

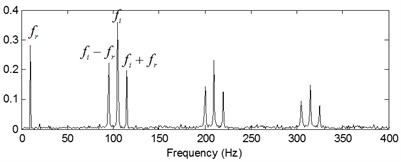
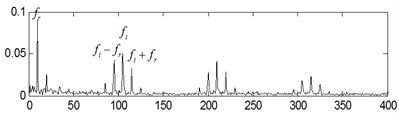
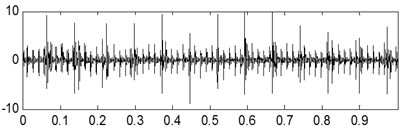
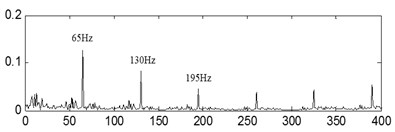
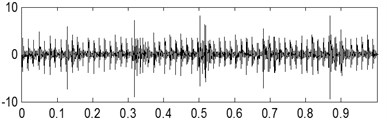
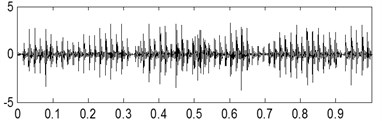
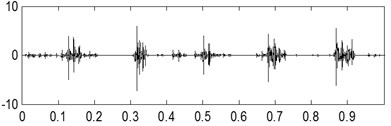
The time-domain waveforms of the three kinds of compound fault are shown in Fig. 15(a), Fig. 16(a) and Fig. 17(a) respectively, and their corresponding envelope demodulation spectrums are given in Fig. 15(d), Fig. 16(d) and Fig. 17(e). In Fig. 15(d), the spectral lines are relative chaotic and the inner race and outer race fault characteristic frequencies with their harmonic frequencies are interleaving together, so it is hard to identify the fault sources. In Fig. 16(d), the outer race fault characteristic frequency with its harmonic frequencies are extracted perfectly using the envelope demodulation method. However, the rolling element fault feature could not be obtained from Fig. 16(d). In Fig. 17(e), Its spectral lines structure is more complex than the spectral lines structure shown in Fig. 15(d) and Fig. 16(d). Though the inner race fault characteristic basic frequency could be extracted roughly, it is evident the spectral lines are chaotic and useful fault features of the outer race fault and rolling element fault could not be obtained based on Fig. 17(e). These analysis results verify that the traditional envelope demodulation spectrum signal processing method is not fit for handling the vibration signal of rolling element baring’ compound fault.

Fig. 14The mean value of correlation coefficients for each clustering number of the three kinds of compound fault

a)

b)

c)

The last separation results of the signal shown in Fig. 15(a) are shown in Fig. 15(b) and Fig. 15(c) based on the proposed method, and their corresponding envelope demodulation spectrums are given in Fig. 15(e) and Fig. 15(f) from which the outer race and inner race fault characteristic frequencies with their harmonic frequencies are extracted successfully and expressed clearly.

Fig. 15The first kind of compound fault with its analysis results

a)

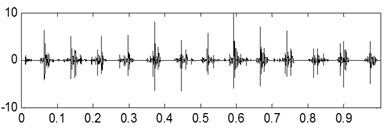
b)

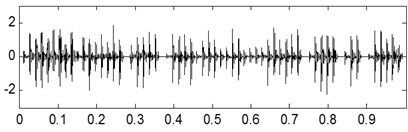
c)

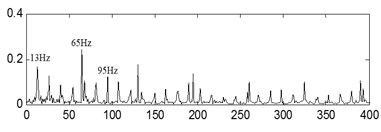
d)

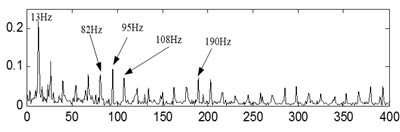
e)

f)

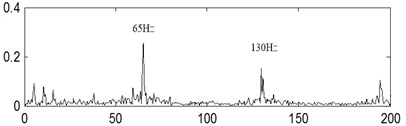
The last separation results of the signal shown in Fig. 16(a) are shown in Fig. 16(b) and Fig. 16(c) based on the proposed method, and their corresponding envelope demodulation spectrums are given in Fig. 16(e) and Fig. 16(f) from which the outer race and inner race fault characteristic frequencies with their harmonic frequencies are extracted successfully and expressed clearly.

Fig. 16The second kind of compound fault with its analysis results

a)

b)

c)

d)

e)

f)

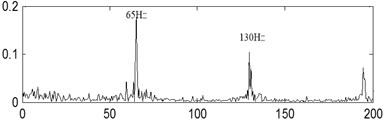
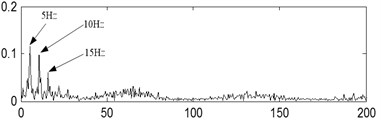
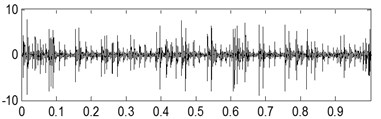
Fig. 17The third kind of compound fault with its analysis results

a)

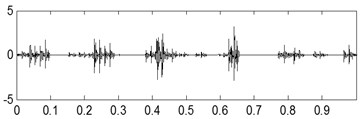
b)

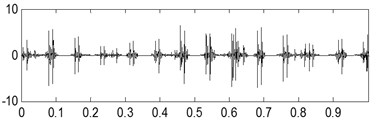
c)

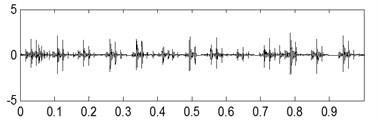
d)

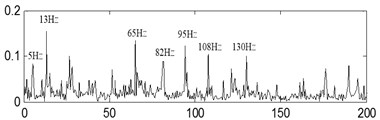
e)

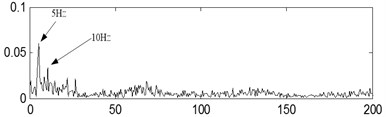
f)

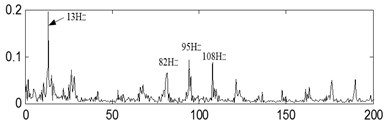
g)

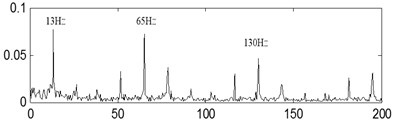
h)

The last separation results of the signal shown in Fig. 17(a) are shown in Fig. 17(b), Fig. 17(c) and Fig. 17(d) based on the proposed method, and their corresponding envelope demodulation spectrums are given in Fig. 17(f), Fig. 17(g) and Fig. 17(h) from which the outer race and inner race fault characteristic frequencies with their harmonic frequencies are also extracted successfully and expressed clearly. These analysis results verify that the proposed method in the paper is fit for blind source separation the compound fault signals arising in rolling element bearing.

6. Conclusions

How to use shift invariant sparse coding idea to solve the problem of compound fault signal analysis is studied. Combining the characteristics of rolling element bearing fault signal, a method for blind source separation of single channel compound fault is proposed based on shift invariant sparse coding and adaptive clustering. The source number is estimated by minimize the structural correlation among source signals. Through simulation, the process and the effect of the method are introduced. The experimental analysis results further show that the proposed method can separate different source signals caused by different type of fault effectively.