The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures

Ergene, Lale T.; Ertuğrul, Yasemin D.

doi:10.21595/jve.2017.18257

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2017

Check for updates

The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures

Lale T. Ergene¹

Yasemin D. Ertuğrul²

^{1, 2}Istanbul Technical University, Istanbul, Turkey

Corresponding Author:

Lale T. Ergene

Cite the article Download PDF

Downloads 2307

CrossRef Citations 2

Abstract

The paper presents the closed-form solution of two dimensional (2D) electromagnetic wave equation for eddy current problems in cylindrical structures. The magnetic field calculation is a complex issue for electrical machines especially. The paper provides an analytical solution for solid cylindrical structures with linear magnetization. This approach is extended to the electrical machines with the solid rotors. Multilayered cylindrical geometry is used for the solution. Two dimensional parabolic partial differential equation is solved for each layer. According to the analytical solution, eddy current and eddy current losses are calculated in the solid region and compared to the results of the finite element model.

1. Introduction

The magnetic field calculation is a very important issue for the electrical machine designers. In the literature, there are different approaches to obtain the magnetic field by using analytical methods, equivalent circuit model, reluctance mesh method or numerical methods. Solving the governing partial differential equations for different boundary conditions analytically is not very easy problem. Because of that the numerical methods such as Finite Element Analysis (FEA) is preferred over the analytical methods for the electrical machine most of time [1]. However, closed form solution of magnetic field provides a fast and approximated solution of the field analysis for the beginning of the design. According to magnetic field calculation with analytical method, sizing equations of motors can be refined easily.

Magnetic field analyses are achieved for different type of motors with different methodologies. The induction machines are analyzed with the analytical methods in the literature. For example, Poynting’s theorem is used for the calculating output power and joule losses [2]. In another study, reluctance network method is used for to determine eddy current in the stator core [3]. Equivalent circuit method is used with new approach in canned solid rotor induction machine [4]. The eddy current calculation is realized in solid conducting region using transverse alternating magnetic field [5]. In some of applications, finite element method and analytical method are combined to decrease the analytical method complexity [6]. The motor with permanent magnet rotor has analytical solution using closed form solution of Maxwell equations [7, 8]. In this study, there is no current source and stator is solid conductor with eddy current. Double Fourier series are applied on the motor with slotless permanent magnet rotor with current layer, which correspond to time and space harmonics [9].

In this paper, the induction motor is modelled as three concentric cylindrical layers representing the different regions showing different material properties. The governing two dimensional partial differential equations are solved for the source, conducting, and non-conducting regions including air gap. The MATLAB^® is used for the analytical calculations. Accuracy of the method is verified with the finite element simulations. This method is applied in rotating cylinder excited by a stationary coil. Then the importance of this method is emphasized for different motor applications in future works [10].

2. Electromagnetic vibration

The magnetic forces between stator and rotor because of the attraction and the repulsion cause the magnetic vibration. These magnetic forces can be in low and high frequency ranges. The low frequency range includes slip frequency and once, twice and higher multiples of the fundamental frequency. The high frequency range includes frequencies related to the product of the number of the rotor slots and the rotational speed of the rotor. These frequencies may be up to kHz for small machines while they may be as low as a few hundred Hz for large machines with a high number of poles. The magnetic vibrations are dominated by the flux flowing between air gap producing rotating force waves. Other combinations of stator and rotor space harmonics and saturation harmonics can also lead to important magnetic vibrations.

The magnetic stored energy in the air gap can be obtained from the total flux density, which is the sum of the rotor and stator flux densities. The total stored energy in the air gap changes while rotor rotates, and a torque occurs. The total flux density in the air gap with respect to time and space is [11]:

1

B_{t o t} (θ, t) = B_{r o t o r} (θ, t) + B_{s t a t o r} (θ, t) .

$B_{r o t o r} (θ, t)$ and $B_{s t a t o r} (θ, t)$ are the form of:

2

\sum_{m} \sum_{k} B_{m k} c o s (m p θ + k ω_{0} t) .

The source of electromagnetic vibration can be traced to the harmonics of the magnetic flux density distribution. Moreover, the flux density analysis can also give information about the torque profile. In a symmetrical stator winding, the MMF harmonic components are phase-belt harmonics with order of ( $2 q \pm 1$ ), stator slot harmonics with order of ( $N_{s} \pm p$ ), and rotor slot harmonics with order of ( $N_{r} \pm p$ ). In the case, the stator doesn’t have the slots so stator harmonic components will not be considered. The MMF distribution in the air gap can be given as Eq. (3) [11]:

3

M M F = A c o s (p θ - ω t)

+ B c o s ((2 q - 1) p θ + ω t) + C c o s ((2 q + 1) p θ - ω t) + D c o s ((N_{s} - p) θ + ω t) + E c o s ((N_{s} + p) θ - ω t) + F c o s ((N_{r} - p) θ - [(1 - s) N_{r} - p] \frac{ω}{p} t) + G c o s ((N_{r} + p) θ - [(1 - s) N_{r} + p] \frac{ω}{p} t) + \dots .

Magnetic flux can cross the interface between air and infinitely permeable material only in a direction perpendicular to the surface of the material. A magnetic force is occurred in the direction of flux. The magnitude of the force is given by in units of pressure or force per unit area:

4

p = \frac{B^{2}}{2 μ_{0}},

where $B$ is the magnetic flux density in Wb/m² and $μ_{0}$ is the permeability of free space (4 $π$ ×10^-7 H/m). The analysis of the $B$ field is very critical to understand the harmonic components of electromagnetic forces since the electromagnetic forces are often found to be the major noise and vibration source in many cases. Because of this reason, the analytical approach is focused on the determining the magnetic vector potentials and flux density for the solid rotor structures. Eddy currents and resulting extra losses because of the solid structure will be affecting the system efficiency. The analytical calculation of eddy current losses is also given in the paper.

3. Physical description

The cross-sectional model of the solid rotor induction motor is shown in Fig. 1. The rotor region is an eddy current region. Moment is created by the rotor magnetic field which arises from eddy current in the rotor. The region lying between $r_{2} < r < r_{3}$ in Fig. 1 is the stationary region called the stator (Region 3). The region lying between $r_{1} < r < r_{2}$ is a bounded free space called air gap between stator and rotor (Region 2). The eddy current region is defined where $0 < r < r_{1}$ (Region 1) and called ‘rotor’. Beyond the stator where $r_{3} < r < \infty$ is the free region (Region 4). Stator magnetic field passes through rotor over the air gap. The current density is given between air gap and stator yoke (current sheet).

Fig. 1Two dimensional cross-sectional of a solid rotor motor model

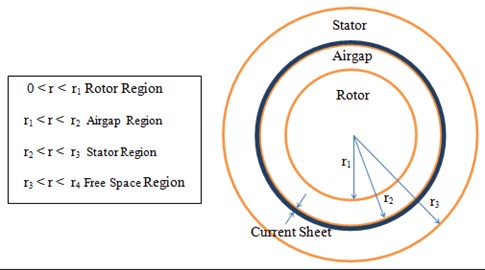
Calculations are made in cylindrical coordinate system. The following is a summary of some of main limitations:

• The problem is considered as two dimensional and linear.

• End effects are neglected.

• The permeability ( $μ_{r 1}$ , $μ_{r 3}$ ) and conductivity ( $σ$ ) of materials are time invariant and independent of the field.

• Saturation and hysteresis effects are neglected.

• The stator is laminated and induced eddy current are neglected.

• The stator current source is represented by a current sheet on the inner bore of the stator.

• The rotor is solid and the permeability and conductivity are isotropic and single valued.

• The field solution is obtained in cylindrical polar coordinates.

• The vector potential has only a ‘ $z$ ’ directed component equal to $A_{z}$ .

• The flux density has two components $B_{r}$ and $B_{θ}$ .

4. Closed form solution

4.1. Formulation

Derivation of the two dimensional time-harmonic eddy current is supplied using diffusion equations in the cylindrical polar coordinates. Maxwell equations are written for every region of the solid rotor motor:

5

\nabla \times H = J_{e} + J_{s},

6

\nabla \times H = \nabla \times \frac{1}{μ_{0} μ_{r}} B = \nabla \times \frac{1}{μ_{0} μ_{r}} \nabla \times A = J_{e} + J_{s} .

Ampere’ Law is given in Eq. (5) and Eq. (6) where $H$ is the magnetic field intensity, $B$ is the magnetic flux density, $A$ is the magnetic vector potential, $J_{e}$ and $J_{s}$ are the eddy current density and source current density, and $μ_{0}$ and $μ_{r}$ represents permeability of space and relative permeability of the material. According to Faraday’s Law, relationship of the electric field and the magnetic flux density are given in Eq. (7). The relationship of the electric field and the magnetic flux density are written in Eq. (7) and Eq. (8) by using $B = \nabla \times A$ and $J = σ E$ equations, where $E$ is the electric field:

7

\nabla \times E = - \frac{\partial B}{\partial t} = - \frac{\partial (\nabla \times A)}{\partial t},

8

\nabla \times H = \frac{1}{μ_{0} μ_{r}} \nabla \times \nabla \times A = - σ \frac{\partial A}{\partial t} + J_{s} .

Using vector identity rule, curl of the magnetic field becomes in Eq. (9):

9

\nabla \times \nabla \times A = \nabla^{2} A = σ μ_{0} μ_{r} \frac{\partial A}{\partial t} + {μ_{0} μ_{r} J}_{s} .

The magnetic vector potential is assumed to be $A = |A| e^{j ω t}$ . The defined problem is in two-dimensional and magnetic flux density has two components which are $B_{r}$ and $B_{θ}$ in polar coordinates and magnetic vector potential has only $z$ component according to relationship with $B$ and $A$ . The magnetic vector potential is written using trigonometric equivalent in Eq. (10) and then obtained derivative using trigonometric identities in Eq. (11):

10

A = |A| (\cos (j ω t) + j s i n (j ω t)),

11

\frac{\partial A}{\partial t} = |A| e^{J ω t} (jω \sin (j ω t) - j^{2} ω c o s (j ω t)) = ω A .

In polar coordinates, $A$ has only $z$ – component and curl of magnetic field in $z$ direction is represented in Eq. (12). The curl of magnetic vector potential is equal to the difference of the current densities which are eddy current and source current density. In polar coordinates:

12

\nabla^{2} A = \frac{\partial^{2} A}{\partial r^{2}} + \frac{1}{r} \frac{\partial A}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} A}{\partial θ^{2}},

13

\frac{\partial^{2} A}{\partial r^{2}} + \frac{1}{r} \frac{\partial A}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} A}{\partial θ^{2}} = j ω μ_{0} μ_{r} σ A - μ_{0} μ_{r} J_{s} .

The motor regions have different magnetic and electrical properties which are given Table 1. These properties of materials require solving partial differential equations in Eq. (13).

Table 1Properties of motor regions

Regions	Properties
Region 1 (rotor)	$J_{s} =$ 0, $μ_{r 1}$ , $σ$
Region 2 (air gap)	$μ_{0}$
Region 3 (stator)	$J_{s} =$ 0, $μ_{r 3}$ , $σ =$ 0
Region 4 (free space)	$μ_{0}$

Region 1 is the eddy current region where $J_{s} =$ 0, characterized by two dimensional diffusion equations in polar coordinates. It is represented in Eq. (14):

14

\frac{\partial^{2} A}{\partial r^{2}} + \frac{1}{r} \frac{\partial A}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} A}{\partial θ^{2}} = j ω μ_{0} μ_{r} σ A .

The diffusion equation which is parabolic partial differential equation solved with separation of variables method. Magnetic vector potential can be separate two different variables and then diffusion equations is refreshed which is given Eq. (15) and Eq. (16):

15

A = R (r) Θ (θ),

16

\frac{r^{2}}{R (r)} \frac{\partial^{2} R (r)}{\partial r^{2}} + \frac{r}{R (r)} \frac{\partial R (r)}{\partial r} + \frac{1}{Θ (θ)} \frac{\partial^{2} Θ (θ)}{\partial θ^{2}} = j ω σ μ_{0} μ_{r} r^{2} .

In closed form, the equation can be written as Eq. (17):

17

r^{2} \frac{R^{''}}{R} + r \frac{R^{'}}{R} + \frac{Θ^{''}}{Θ} = j ω σ μ_{0} μ_{r} r^{2} .

Eq. (17) can be simplified with using coefficients which is $- n^{2}$ and $k^{2}$ to transform into a second order ordinary differential equation given in Eq. (18):

18

r^{2} R^{''} + r R^{'} - (n^{2} + j k^{2} r^{2}) R = 0 .

Eq. (18) can be expressed as a parametric Bessel equation which is written in general form in Eq. (19) [12]. ‘ $j k^{2}$ ’ term is simplified as $β^{2}$ to simulate parametric modified Bessel equation:

19

r^{2} R^{''} + r R^{'} - (β^{2} r^{2} + n^{2}) R = 0 .

The parametric modified Bessel equation solution has two components which are given in Eq. (20):

20

R = A I_{n} (\sqrt{j k r}) + B K_{n} (\sqrt{j k r}) .

$I_{n}$ and $K_{n}$ are the modified Bessel’s functions and $n$ is the order of equation and represented as $b e r$ and $b e i$ functions:

21

I_{n} (k r) = B e r (k r) + j B e i (k r),

22

K_{n} (k r) = K e r (k r) + j K e i (k r) .

First part of the Eq. (15) is arranged in Eq. (23) with modified Bessel’s functions:

23

R (r) = \sum_{l}^{n} C_{n} [B e r_{n} (k r) + j B e i_{n} (k r)] + D_{n} [K e r_{n} (k r) + j K e i_{n} (k r)] .

Using the separation of variables method, second part of the separated variable is given in Eq. (24):

24

\frac{Θ^{''}}{Θ} = - n^{2}, Θ^{''} + n^{2} Θ = 0 .

This is ordinary differential equation and solved as Eq. (25):

25

Θ (θ) = C_{1} (\cos (n θ) + j s i n (n θ)) + C_{2} (\cos (- n θ) + j s i n (- n θ)) .

The general solution of Eq. (25) is given as summation of cosine and sinus functions in Eq. (26) which is arranged and simplified:

26

Θ (θ) = \sum_{l}^{n} E_{n} \cos (n θ) + F_{n} \sin (n θ) .

The solution of magnetic vector potential is related with $r$ and $θ$ by use of the separation of variables method shown in Eq. (27):

27

A = \sum_{l}^{n} {[C}_{n} [B e r_{n} (k r) + j B e i_{n} (k r)] + D_{n} [K e r_{n} (k r) + j K e i_{n} (k r)]] [E_{n} \cos (n θ) + F_{n} s i n (n θ)] .

The magnetic vector potential equation is given in Eq. (27). This equation is represented by trigonometric equations comes from modified Bessel functions.

4.2. Calculation for regions

The closed form of the diffusion equation is solved with the separation of variables method. The found magnetic vector potential equation can be used for every regions and boundaries. Eq. (27) can be applied every region of the model given in Fig. 1. According to regions magnetic and electrical properties, coefficients of the magnetic vector potential are simplified.

Region 1: ( $0 < r < r_{1}$ ) In rotor region, the field at $r =$ 0 is finite and has only cosine components, we have $D_{n} =$ 0 and $F_{n} =$ 0. The rotor has electrical conductivity and it is called the eddy current region. The magnetic vector potential of rotor regions is given in Eq. (28):

28

A_{1} = \sum_{1}^{n} C_{1 n} [B e r_{n} (k r) + j B e i_{n} (k r)] \cos (n θ) .

Region 2: ( $r_{1} < r < r_{2}$ ) The air gap region is between $r_{1}$ and $r_{2}$ and magnetic vector potential is in Eq. (29):

29

A_{2} = \sum_{1}^{n} (C_{2 n} r^{n} + D_{2 n} r^{- n}) \cos (n θ) .

Region 3: ( $r_{2} < r < r_{3}$ ) The stator region has no electrical conductivity and it is eddy current free region and represented magnetic vector potential in Eq. (30):

30

A_{3} = \sum_{1}^{n} (C_{3 n} r^{n} + D_{3 n} r^{- n}) \cos (n θ) .

Region 4: ( $r_{3} < r < \infty$ ) The last air region begins from the stator outer diameter to infinite. The magnetic vector potential is in below as in Eq. (31):

31

A_{4} = \sum_{1}^{n} (D_{4 n} r^{- n}) \cos (n θ) .

Normal component of the magnetic flux density ( $B_{r}$ ), and tangential components of the magnetic field ( $H_{θ}$ ) are equal to each other at boundaries. Therefore, the boundary conditions:

32

r = r_{3}, B_{r 3} = B_{r 4}, H_{θ 3} = H_{θ 4},

33

r = r_{2}, B_{r 2} = B_{r 3}, H_{θ 2} - H_{θ 3} = J_{s},

34

r = r_{1}, B_{r 1} = B_{r 2}, H_{θ 1} = H_{θ 2},

35

B = \nabla \times A = \frac{1}{r} \frac{\partial A}{\partial θ} r - \frac{\partial A}{\partial r} θ,

36

B_{r} = \frac{1}{r} \frac{\partial A}{\partial θ} B_{θ} = - \frac{\partial A}{\partial r} .

The magnetic flux densities and the field intensities for each region are obtained from magnetic vector potential equations and given in Eqs. (37-44).

Region 4 equations:

37

B_{r 4} = \frac{1}{r} \frac{\partial A_{4}}{\partial θ} = \sum_{1}^{n} (- n D_{4 n} r^{- n}) s i n (n θ),

38

H_{θ 4} = \frac{B_{θ 4}}{μ_{0}} = - \frac{1}{μ_{0}} \frac{\partial A_{4}}{\partial r} = \sum_{1}^{n} (\frac{n}{μ_{0}} D_{4 n} r^{- n - 1}) \cos (n θ) .

Region 3 equations:

39

B_{r 3} = \frac{1}{r} \frac{\partial A_{3}}{\partial θ} = \sum_{1}^{n} - n (C_{3 n} r^{n - 1} + D_{3 n} r^{- n - 1}) s i n (n θ),

40

H_{θ 3} = \frac{B_{θ 3}}{μ_{0} μ_{r 3}} = - \frac{1}{μ_{0} μ_{r 3}} \frac{\partial A_{3}}{\partial r} = \sum_{1}^{n} - \frac{n}{μ_{0} μ_{r 3}} ({C_{3 n} r^{n - 1} - D}_{3 n} r^{- n - 1}) \cos (n θ) .

Region 2 equations:

41

B_{r 2} = \frac{1}{r} \frac{\partial A_{2}}{\partial θ} = \sum_{1}^{n} - n (C_{2 n} r^{n - 1} + D_{2 n} r^{- n - 1}) s i n (n θ),

42

H_{θ 2} = - \frac{1}{μ_{0}} \frac{\partial A_{2}}{\partial r} = \sum_{1}^{n} - \frac{n}{μ_{0}} ({C_{2 n} r^{n - 1} - D}_{2 n} r^{- n - 1}) \cos (n θ) .

Region 1 equations:

43

B_{r 1} = \frac{1}{r} \frac{\partial A_{1}}{\partial θ} = \sum_{1}^{n} - n \frac{C_{1 n}}{r} [B e r_{n} (k r) + j B e i_{n} (k r)] \sin (n θ),

44

H_{θ 1} = \frac{B_{θ 1}}{μ_{0} μ_{r 1}} = - \frac{1}{μ_{0} μ_{r 1}} \frac{\partial A_{1}}{\partial r} = \sum_{1}^{n} - n k \frac{C_{1 n}}{μ_{0} μ_{r 1}} [B e r_{n}^{'} (k r) + j B e i_{n}^{'} (k r)] \cos (n θ) .

The boundary conditions are considered to find coefficients of the magnetic flux densities. The normal component of magnetic flux densities ( $B_{r}$ ), and the tangential components of magnetic field intensities ( $H_{θ}$ ) are equal to each other at boundaries related to each region.

At the boundary of $r = r_{3}$ , the boundary conditions of $B_{r 3} = B_{r 4}$ , $H_{θ 3} = H_{θ 4}$ should be satisfied. The related equations are given in Eq. (45) to find out $D_{3 n}$ and $C_{3 n}$ coefficients in terms of $D_{4 n}$ . The revised equations are given in Eqs. (46-47):

45

\sum_{1}^{n} - n (C_{3 n} r_{3}^{n - 1} + D_{3 n} r_{3}^{- n - 1}) \sin (n θ) = \sum_{1}^{n} (- n D_{4 n} r_{3}^{- n}) \sin (n θ),

\sum_{1}^{n} - \frac{n}{μ_{0} μ_{r 3}} ({C_{3 n} r_{3}^{n - 1} - D}_{3 n} r_{3}^{- n - 1}) \cos (n θ) = \sum_{1}^{n} (\frac{n}{μ_{0}} D_{4 n} r_{3}^{- n - 1}) \cos (n θ),

D_{3 n} = D_{4 n} (\frac{1 + μ_{r 3}}{2}), C_{3 n} = D_{4 n} (\frac{1 - μ_{r 3}}{2}) r_{3}^{- 2 n},

46

B_{r 3} = \sum_{1}^{n} [- \frac{n D_{4 n}}{2} r^{- n - 1} [(1 - μ_{r 3}) r_{3}^{- 2 n} r^{2 n} + (1 + μ_{r 3})] s i n (n θ)],

47

H_{θ 3} = \sum_{1}^{n} [- \frac{n}{2 μ_{r 3} μ_{0}} D_{4 n} r^{- n - 1} [(1 - μ_{r 3}) {(\frac{r}{r_{3}})}^{2 n} - (1 + μ_{r 3})] c o s (n θ)] .

At the boundary of $r = r_{1}$ , the boundary conditions of $B_{r 1} = B_{r 2}$ , $H_{θ 1} = H_{θ 2}$ should be satisfied. The related equations are given in Eq. (48) to find out $D_{2 n}$ and $C_{2 n}$ coefficients in terms of $C_{1 n}$ . The revised equations are given in Eqs. (51-52):

48

\sum_{1}^{n} - \frac{n C_{1 n}}{r_{1}} [B e r_{n} (k r_{1}) + j B e i_{n} (k r_{1})] \sin (n θ) = \sum_{1}^{n} - n (C_{2 n} r_{1}^{n - 1} + D_{2 n} r_{1}^{- n - 1}) \sin (n θ),

\sum_{1}^{n} - \frac{n k C_{1 n}}{μ_{0} μ_{r 1}} [B e r_{n}^{'} (k r_{1}) + j B e i_{n}^{'} (k r_{1})] \cos (n θ)

= \sum_{1}^{n} - \frac{n}{μ_{0}} ({C_{2 n} r_{1}^{n - 1} - D}_{2 n} r_{1}^{- n - 1}) \cos (n θ),

C_{2 n} = \frac{C_{1 n}}{2} (\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) r_{1}^{- n + 1}, D_{2 n} = \frac{C_{1 n}}{2} (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) r_{1}^{n + 1},

where:

49

P = B e r_{n} (k r_{1}) + j B e i_{n} (k r_{1}),

50

Q = B e r_{n}^{' (k r_{1})} + j B e i_{n}^{'} (k r_{1}),

51

B_{r 2} = \sum_{1}^{n} - \frac{n C_{1 n}}{2} [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{- n - 1}] \sin (n θ),

52

H_{θ 2} = \sum_{1}^{n} - \frac{n C_{1 n}}{2 μ_{0}} [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{- n - 1}] c o s (n θ) .

At the boundary of $r = r_{2}$ , the boundary conditions of $B_{r 2} = B_{r 3}$ , $H_{θ 3} - H_{θ 2} = J_{s}$ should be satisfied. The related equations are given in Eq. (54) to find out $D_{4 n}$ and $C_{1 n}$ coefficients. $E$ and $F$ expressions given in Eq. (53) are used to simplify the equations:

53

E = (1 - μ_{r 3}) {(\frac{r}{r_{3}})}^{2 n} + (1 + μ_{r 3}), F = (1 - μ_{r 3}) {(\frac{r}{r_{3}})}^{2 n} - (1 + μ_{r 3}),

54

\sum_{1}^{n} - \frac{n C_{1 n}}{2} [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{- n - 1}] \sin (n θ) = \sum_{l}^{n} [- \frac{n D_{4 n}}{2} {r_{2}}^{- n - 1} E \sin (n θ)],

\sum_{1}^{n} [- \frac{n}{2 μ_{r 3} μ_{0}} D_{4 n} {r_{2}}^{- n - 1} F c o s (n θ)] - \sum_{1}^{n} - \frac{n C_{1 n}}{2 μ_{0}} [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{- n - 1}] \cos (n θ) = \sum_{1}^{n} J_{s} \cos (n θ) .

With the boundary conditions, all of the coefficients are obtained which are involved in the equations of magnetic vector potential, magnetic field intensity and also magnetic flux density. Coefficients are given in Eqs. (59-60):

55

C_{1 n} = \frac{2 μ_{0} J_{s} E}{V (\frac{E U}{V} - \frac{F}{μ_{r 3}})},

56

D_{4 n} = \frac{2 μ_{0} J_{s} {r_{2}}^{n + 1}}{(\frac{E U}{V} - \frac{F}{μ_{r 3}})},

57

C_{2 n} = \frac{μ_{0} J_{s} E {r_{1}}^{- n + 1} (\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}})}{V (\frac{E U}{V} - \frac{F}{μ_{r 3}})},

58

D_{2 n} = \frac{μ_{0} J_{s} E {r_{1}}^{n + 1} (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}})}{V (\frac{E U}{V} - \frac{F}{μ_{r 3}})},

59

C_{3 n} = \frac{μ_{0} J_{s} {r_{2}}^{n + 1} {r_{3}}^{- 2 n} (1 - μ_{r 3})}{(\frac{E U}{V} - \frac{F}{μ_{r 3}})},

60

D_{3 n} = \frac{μ_{0} J_{s} {r_{2}}^{n + 1} (1 + μ_{r 3})}{(\frac{E U}{V} - \frac{F}{μ_{r 3}})} .

In these equations, some reductions carried out to arrange equations which are ‘ $U$ ’ and ‘ $V$ ’ which are given as follows:

61

U = (\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{n - 1} - (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{- n - 1},

62

V = (\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r_{2}}{r_{1}})}^{- n - 1} .

Since all the integration constants have been determined, the respective vector potentials, the radial components of the flux-densities and the tangential components of the magnetic fields in the different regions are obtained as follows.

Region 1:

63

A_{1} = \sum_{1}^{n} \frac{- 2 μ_{0} J_{s} E [B e r_{n} (k r) + j B e i_{n} (k r)]}{V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ),

64

B_{r 1} = \sum_{1}^{n} \frac{2 n μ_{0} J_{s} E [B e r_{n} (k r) + j B e i_{n} (k r)]}{V r (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \sin (n θ),

65

H_{θ 1} = \sum_{1}^{n} \frac{2 n k J_{s} E [B e r_{n}' (k r) + j B e i_{n}' (k r)]}{μ_{r 1} V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ) .

Region 2:

66

A_{2} = \sum_{1}^{n} \frac{- μ_{0} J_{s} E r_{1} [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{n} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{- n}]}{V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ),

67

B_{r 2} = \sum_{1}^{n} \frac{n μ_{0} J_{s} E [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{n - 1} + (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{- n - 1}]}{V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \sin (n θ),

68

H_{θ 2} = \sum_{1}^{n} \frac{n J_{s} E [(\frac{P}{r_{1}} + \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{n - 1} - (\frac{P}{r_{1}} - \frac{k Q}{μ_{r 1}}) {(\frac{r}{r_{1}})}^{- n - 1}]}{V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ) .

Region 3:

69

A_{3} = \sum_{1}^{n} \frac{- μ_{0} J_{s} r_{2}^{n + 1} [(1 - μ_{r 3}) r_{3}^{- 2 n} r^{n} + (1 + μ_{r 3}) r^{- n}]}{(\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ),

70

B_{r 3} = \sum_{1}^{n} \frac{n μ_{0} J_{s} r_{2}^{n + 1} [(1 - μ_{r 3}) r_{3}^{- 2 n} r^{n - 1} + (1 + μ_{r 3}) r^{- n - 1}]}{(\frac{F}{μ_{r 3}} - \frac{E U}{V})} \sin (n θ),

71

H_{θ 3} = \sum_{1}^{n} \frac{n μ_{0} J_{s} r_{2}^{n + 1} [(1 - μ_{r 3}) r_{3}^{- 2 n} r^{n - 1} - (1 + μ_{r 3}) r^{- n - 1}]}{μ_{r 3} (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ) .

Region 4:

72

A_{4} = \sum_{1}^{n} \frac{- {2 μ}_{0} J_{s} r_{2}}{(\frac{F}{μ_{r 3}} - \frac{E U}{V})} {(\frac{r}{r_{2}})}^{- n} \cos (n θ),

73

B_{r 4} = \sum_{1}^{n} \frac{{2 n μ}_{0} J_{s}}{(\frac{F}{μ_{r 3}} - \frac{E U}{V})} {(\frac{r}{r_{2}})}^{- n - 1} \sin (n θ),

74

H_{θ 4} = \sum_{1}^{n} \frac{2 n J_{s}}{(\frac{F}{μ_{r 3}} - \frac{E U}{V})} {(\frac{r}{r_{2}})}^{- n - 1} \cos (n θ) .

The eddy current density in eddy current region is given in the Eq. (75), by using the Eq. (63):

75

{J_{e} = - j ω σ A}_{1} = \sum_{1}^{n} \frac{2 j ω σ μ_{0} J_{s} E [B e r_{n} (k r) + j B e i_{n} (k r)]}{V (\frac{F}{μ_{r 3}} - \frac{E U}{V})} \cos (n θ) .

After deriving the current density equation, the power loss in eddy current region can be obtained by using Eq. (76) in polar coordinates:

76

P_{e} = \int_{0}^{2 π} \int_{0}^{l} \int_{0}^{r_{1}} \frac{J_{e} J_{e}^{*}}{2 σ} r d r d θ d z .

Substituting $J e$ from Eq. (75) and its conjugate in Eq. (76) for power loss, one obtains after some algebraic manipulation:

77

P_{e} = 4 p s^{2} ω^{2} μ_{0}^{2} σ J_{s}^{2} E^{2} π l \frac{\frac{r_{1}}{k} [B e r_{n} (k r_{1}) B^{'} e i_{n} (k r_{1}) + B' e r_{n} (k r_{1}) B e i_{n} (k r_{1})]}{V V^{*} (\frac{F}{μ_{r 3}} - \frac{E U}{V}) {(\frac{F}{μ_{r 3}} - \frac{E U}{V})}^{*}} .

5. Finite element model

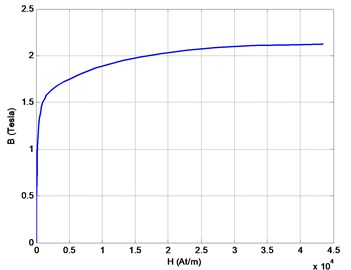
The finite element model of the solid rotor structure is constructed to verify and compare the analytical model. The magnetic material used in both rotor ( $μ_{r 1}$ ) and the stator ( $μ_{r 3}$ )is given in Fig. 2. The flux density through the air gap is calculated by the finite element results of solid rotor induction motor. Calculations are obtained for different operating conditions of the motor. The rotor has the conductivity also. The motor has 4 kW 380 V 1459 min^-1, 50 Hz power ratings.

Fig. 2Magnetization curve of the stator and rotor material

The current density of the solid rotor motor is created by three phase stator currents. The current source of the solid rotor motor is given as the first harmonic of the signal in the solid rotor machine:

78

J_{s} = J_{S} \cos (n θ) .

The line current density injected in the FEM model to make the model similar to the analytical. The injected line current in the motor and the motor mesh are shown in Fig. 3. The rotor conductivity σ is chosen as 3×10⁶ S/m in both analytical and numerical calculations. $μ_{r 1}$ and $μ_{r 3}$ are defined in the linear region as 750. The air region permeability is $μ_{0} =$ 4 $π$ 10^-7 H/m. The length of the rotor is 145 mm. The diameters are as follows: $r_{1} =$ 58.25 mm, $r_{2} =$ 58.5 mm, $r_{3} =$ 85 mm. The frequency is 50 Hz. The output torques at the rated value for the both analytical and numerical models are coherent and the relative error is less than 5 %.

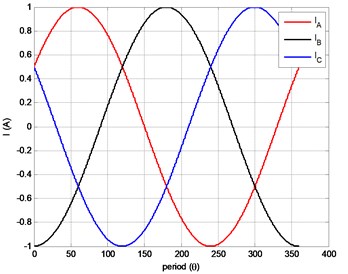
The phase currents for one cycle from the FEM are given in Fig. 4.

Fig. 3The quarter model of the line current density and its mesh

a)

b)

Fig. 4Stator phase currents of solid rotor induction motor.

6. Results

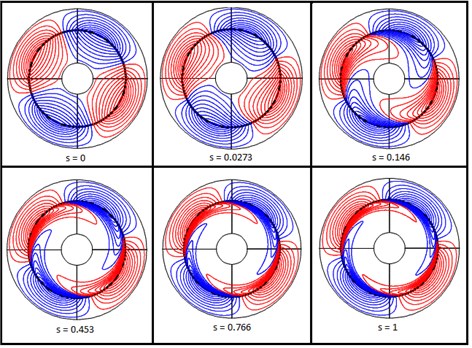
Slip speed of an induction motor is defined as the difference between the synchronous speed and the actual rotor speed. The solid rotor induction machine is analyzed at steady state for different slip values. The equi-flux lines are given in Fig. 5. The skin effect and phase delay because of the eddy currents can be observed with increasing slip value.

Fig. 5Equi-flux lines for different slip values

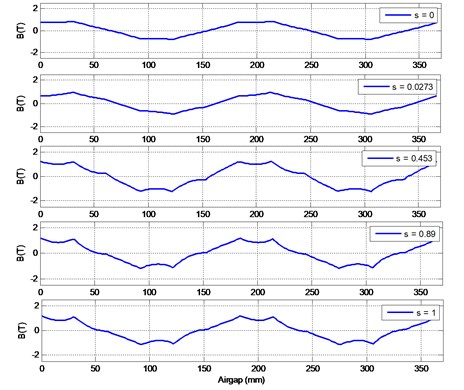
The flux density variation in the air gap for different slip values are given in Fig. 6. The four pole distribution is obvious for each slip value.

Fig. 6Flux density in the air gap for different slip values

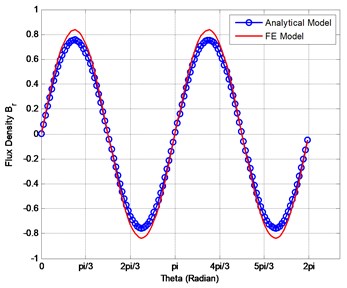
In the analytical model of the solid rotor machine, first harmonic of the air gap flux density is calculated. Fig. 7 shows normal component of the flux density and its first harmonic. Flux density and its harmonics are calculated by the finite element method. The finite element result of the solid rotor induction motor is taken as the reference for analytical calculations. Air gap flux densities are compared with each other in Fig. 8. Calculated first harmonic is compared with the analytical result of the air gap flux density. The results are coherent and the relative error is less than 10 %.

Fig. 7Air gap flux density and its first harmonic with FEM

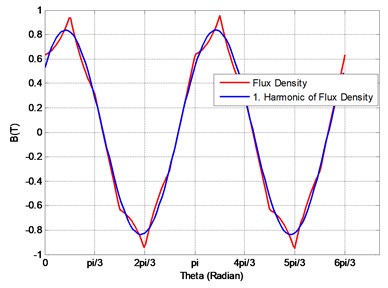
Fig. 8Comparison of the analytical and numerical results of the flux density around the air gap

The finite element and analytical results of eddy current density and eddy current loss for the solid rotor are given in Table 2. They are coherent.

Table 2Comparison of the eddy current density and the power loss in the rotor at the rated operation condition (sN= 2.73 %)

Method	$J_{e}$ (pu)	$P e$ (pu)
FEM model	1	1
Analytical model	1.08	1.12

7. Conclusions

Solid rotor cylindrical structure is analyzed using closed form solution of magnetic field in the case study of a solid rotor induction motor. The analysis is based on the solution of the modified Bessel functions of the parabolic wave equation for an eddy current medium. The obtained analytical expressions have been compared to the finite elements yielding almost the same results for the cylindrical same geometry. Closed-form solution of magnetic fields in induction motors provides a fast and easy method of field analysis, which can help in sizing studies in design and evaluation of performance and in the determination of equivalent circuit parameters. Although a rigorous representation of the geometry is not within the scope of closed-form studies, a quick and easy solution for the eddy current region is obtained. In the paper, a method of evaluating magnetic fields in a cylindrical solid structures are presented and formulae for eddy currents and power losses are derived.

References

Ahfock T., Hewitt A. Modeling of the solid rotor induction motor. 15th Australasian Universities Power Engineering Conference (AUPEC 2005), Hobart, Australia, 2005.

Search CrossRef
Markoviç M., Perriard Y. An analytical solution for the torque and power of a solid-rotor induction motor. Proceedings of IEEE International Electric Machines and Drives Conferences (IEMDC 2011), 2011, p. 1053-1057.

Publisher
Mirzayee M., Mehrjerdi H., Tsurkerman I. Analysis of a high speed solid rotor induction motor using coupled analytical method and reluctance networks. IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetics, Honolulu, Hawaii, 2005.

Search CrossRef
Ergene L. T., Salon S. J. Determining the equivalent circuit parameters of canned solid rotor induction motors. IEEE Transactions on Magnetics, Vol. 41, Issue 7, 2005, p. 2281-2286.

Publisher
Perry M., Jones T. Eddy current induction in a solid conducting cylinder with a transverse magnetic field. IEEE Transactions on Magnetics, Vol. 14, Issue 4, 1978, p. 227-232.

Publisher
Theodoropoulos I., Tatis K., Kladas A., Tegopoulos J. Solid rotor induction machine optimization by using analytical and finite element techniques. Prace Instytutu Elektrotechniki, Vol. 216, 2003, p. 7-16.

Search CrossRef
Markovic M., Perriard Y. An analytical determination of Eddy-current losses in a configuration with a rotating permanent magnet. IEEE Transactions on Magnetics, Vol. 43, Issue 8, 2007, p. 3380-3386.

Publisher
Markovic M., Perriard Y. Analytical solution for Eddy current losses in a slotless permanent magnet motor: the case of current sheet excitation. IEEE Transactions on Magnetics, Vol. 44, Issue 3, 2008, p. 386-393.

Publisher
Markovic M., Pfister P.-D., Perriard Y. Analytical solution for rotor Eddy-current losses in a slotless permanent-magnet motor: the case of current layer excitation. International Conference on Electrical Machines and Systems ICEMS, Tokyo, Japan, 2009.

Publisher
Chari M. K. V., Bedrosian, G. Electromagnetic field analysis of Eddy currents effects in rotating electrical apparatus and machinery. IEEE Transactions on Magnetics, Vol. 18, Issue 6, 1982, p. 1713-1715.

Publisher
Ergene L. T., Donmezer Y. Improved design for minimizing torque ripples at BLDC motors used in washers. International Review of Electrical Engineering, Vol. 5, Issue 5, 2010, p. 2022-2032.

Search CrossRef
McLachlan N.W. Bessel Functions for Engineers. Clarendon Press, Oxford, 1954.

Search CrossRef

Cited by

Kütlesel Rotorlu İndüksiyon Motorlarında Oluşan Eddy Akımlarının Kollokasyon Yöntemi Kullanılarak Çözümü

Hüseyin Yıldız

(2024)

Kütlesel Rotorlu İndüksiyon Motorlarında Oluşan Eddy Akımlarının Kollokasyon Yöntemi Kullanılarak Çözümü

Hüseyin Yıldız

(2024)

About this article

Received

16 February 2017

Accepted

30 April 2017

Published

15 August 2017

SUBJECTS

Oscillations in electrical engineering

DOI

https://doi.org/10.21595/jve.2017.18257

Keywords

electromagnetic wave equation

diffusion equation

parabolic partial differential equations

eddy current

closed form solution

solid rotor

boundary conditions

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 23

Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Baljeet Singh, Himanshu Singla

Research article

2022 01 25

Three-dimensional numerical simulation of multi-physical coupled environment during electromagnetic propulsion

Yuxin Yang, Peng Liu, Haojie Li, He Zhang

Research article

2019 10 19

Design and analysis of magnetic circuit of permanent magnet eddy current brake

Yumeng Fan, Guolai Yang

Research article

2019 10 19

Electromagnetic buffering considering PM eddy current loss under intensive impact load

Zi-Xuan Li, Guo-Lai Yang, Lei Li

L. T. Ergene and Y. D. Ertuğrul, “The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures,” Journal of Vibroengineering, Vol. 19, No. 5, pp. 3911–3925, Aug. 2017, https://doi.org/10.21595/jve.2017.18257

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18257
UR  - https://doi.org/10.21595/jve.2017.18257
TI  - The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures
T2  - Journal of Vibroengineering
AU  - Ergene, Lale T.
AU  - Ertuğrul, Yasemin D.
PY  - 2017
DA  - 2017/08/15
PB  - JVE International Ltd.
SP  - 3911-3925
IS  - 5
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Ergene_2017,
	doi = {10.21595/jve.2017.18257},
	url = {https://doi.org/10.21595/jve.2017.18257},
	year = 2017,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {5},
	pages = {3911--3925},
	author = {Lale T. Ergene and Yasemin D. Ertu{\u{g}}rul},
	title = {The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. T. Ergene and Y. D. Ertuğrul, “The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures,” Journal of Vibroengineering, vol. 19, no. 5, pp. 3911–3925, Aug. 2017, doi: 10.21595/jve.2017.18257.

Copy IEEE

Copied to clipboard!

Ergene, Lale T., and Yasemin D. Ertuğrul. “The Analytical Solution of 2D Electromagnetic Wave Equation for Eddy Currents in the Cylindrical Solid Rotor Structures.” Journal of Vibroengineering 19, no. 5 (August 15, 2017): 3911–25. https://doi.org/10.21595/jve.2017.18257.

Copy Chicago

Copied to clipboard!

The analytical solution of 2D electromagnetic wave equation for eddy currents in the cylindrical solid rotor structures

Abstract

1. Introduction

2. Electromagnetic vibration

3. Physical description

4. Closed form solution

4.1. Formulation

4.2. Calculation for regions

5. Finite element model

6. Results

7. Conclusions

References

Cited by

About this article

Related Articles