Systematical research on the aerodynamic noise of the high-lift airfoil based on FW-H method

1. Introduction

Aerodynamic noises generated by aircrafts are divided into two parts including engine noises and airframe noises. Airframe noises are mainly the sum of aerodynamic noises and mechanical noises caused by the pressure fluctuation [1, 2]. Regarding engine noises, contemporary civil aircrafts widely apply turbofan engines. Usually, fan noises and jet noises are the main noise sources of an engine. Turbofan engines are a typical rotary machine. Therefore, periodic rotating turbine in the engine and the periodic interference will cause typical discrete noises [3-6]. In addition, jet noises are in direct proportion to the 8th power of its jet velocity. As a result, the higher jet velocity is, and the louder jet noises will be. To reduce jet noises, engine noises can be reduced through increasing bypass ratio and slowing down jet velocity. With the increase of bypass ratio of turbofan engines, the exhaust velocity of engines has been decreased. Compared with turbine noises, jet noises are gradually decreased [7-8]. The noise level of engines has been reduced obviously and controlled effectively. Especially when an aircraft enters the site, the engine stays at an idle power state, and the airframe noise has become the main source of aircraft noises. Therefore, airframe noises become the bottleneck for overall noise reduction of an aircraft, where it should draw more and more attention in aircraft noise researches. Airframe noises mainly include leading edge slat noises and trailing edge flap noises [9, 10]. It has been verified in many researches [11-13] that the leading edge slat and trailing edge flap of the high-lift airfoil are the important sound generation component, so controlling leading edge slat and trailing edge flap noises of the high-lift airfoil will become an important step in studying noise reduction of aircrafts.

At present, a lot of numerical and experimental researches have been conducted on generation mechanisms and acoustic characteristics of leading edge slat noises of the high-lift airfoil. Takeda [14, 15] used wind tunnel experiments to test the unsteady flow field of the leading edge slat as well as aerodynamic noise characteristics in this region, captured the trailing edge eddy, and further verified that the trailing edge eddy was the major source for aerodynamic noises of the leading edge slat. However, it is very difficult to conduct experimental researches on leading edge slat noises mainly because that a wind tunnel testing section shall satisfy aerodynamic and acoustic requirements at the same time, but they are generally contradictory. From the perspective of aerodynamics, in order to ensure that flowing around the slat can approach an unbounded flow field as much as possible, the slat should be tested in a closed wind tunnel. However, the wind tunnel is not suitable for acoustic test in general as the reverberation would appear in the closed section and generate additional noises. Choudhari [16] used the numerical simulation technology to simulate the unsteady flow of a three-dimensional eddy structure in a slat cavity. Results show that the free shear layer developed to the downstream and then got attached on the lower surface of the slat, becoming the main source of low-frequency broadband noises; however, numerical simulation results were not verified by experiments, and correctness of the computational model could not be guaranteed. Liu [17] used FLUENT software to simulate the multi-section slat and solved the RANS equation and FW-H equation, where a blowing hole was set under the leading edge slat. Through changing the blowing coefficient, impacts of blowing flows on the aerodynamic noise were studied. However, differences in aerodynamic noises of each section were not analyzed. Based on the Farassat time-domain formula, Xu [18] took the sum of thickness noises and load noises as the total noise, and conducted numerical dispersion of the blade surface along the expansion and chord directions in order to establish a prediction method of slat noises; the method was verified by experiments, but the noise directivity under different Mach numbers was not discussed and analyzed in details. Additionally, the mentioned researches mainly focused on the aerodynamic noise of the leading edge slat of the high-lift airfoil, but the aerodynamic noise of the trailing edge flap of the high-lift airfoil was not considered.

Aiming at those questions, this paper computed the far-field aerodynamic noise of the high-lift airfoil including the leading edge slat and trailing edge flap, analyzed the reason of aerodynamic noises from the perspective of flow mechanism, conducted numerical computation for the far-field aerodynamic noises of all the sections of the high-lift airfoil, and compared the differences of aerodynamic noises caused by all sections. The numerical computation was also verified by experiments, so the research in this paper was very rigorous and systematic.

2. Acoustic analogy method based on FW-H equations

Under the boundary of solid wall surface, the impact of solid wall surface on flow or the fluctuation should be considered through its boundary and further transformed into the problem solving the boundary value of partial differential equation. To apply Green function of infinite space to compute and obtain the boundary value of the partial differential equation, generalized Heaviside function was introduced into the derivation of FW-H equations to extend the computational domain space to infinite space [19-21] and finally derive the expression of FW-H equations, as follows:

Through further processing, FW-H equations which are widely used could be obtained, as follows:

wherein, $\rho$, $u_i$ and $P_{i,j}$ are density, velocity and stress tensor, respectively; ${\rho }_0$ and $p_0$ are unperturbed density and velocity, respectively; $\rho \mathrm{\text{'}}$ and $P_{i,j}^{\text{'}}$ are perturbed density and stress tensor, respectively; $\stackrel{-}{\partial }/\partial t$ and $\stackrel{-}{\partial }/\partial x_j$ are generalized space and time derivative, and $\partial f/\partial t=-v_n$, $\partial f/\partial x_i=n_i$, $v_n$ and $u_n$ are the normal motion velocity of control plane and fluid respectively; $\delta \left(f\right)$ is Dirac function and defined as $\delta \left(f\right)=\stackrel{-}{\partial }H\left(f\right)/\partial f$; $T_{i,j}$ is Lighthill tensor. Here, acoustic integral surface used in the integral formula could be any space surface containing solid [22, 23]. The right side of the equation could also be considered as sound source item and the first item is a quadrupole source; the second item represents a dipole source which is caused by surface fluctuation pressure; the third item is a monopole source which is caused by surface acceleration.

3. The computational model of the high-lift airfoil

3.1. Geometric model

This paper took three-dimensional L1T2 airfoil as the studied object, as shown in Fig. 1. Leading edge slat and trailing edge flap were open and related model sizes were shown in Fig. 2. The chord length and the span-wise length of leading edge slat and trailing edge flap were 1m; the deflection angle ${\delta }_s$ of leading edge slat was 25°; the deflection angle ${\delta }_f$ of trailing edge flap was 20°.

Fig. 1Three-dimensional geometric model of the high-lift airfoil

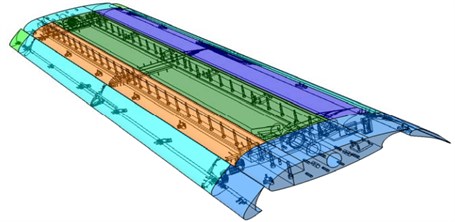
Fig. 2Schematic diagram for the geometric model of L1T2 high-lift airfoil

3.2. Computational grids

Fig. 3 presented full-field and local grids. These were three-dimensional structured C-type topology grids. 226 grid points were arranged along the wall surface of leading edge slat; 512 grid points were arranged along the wall surface in the middle part of the airfoil; 142 grid points were arranged along the wall surface of trailing edge flap; 51 grid points were uniformly arranged along the span-wise direction. Regarding boundary layer grids on the solid wall surface, the first layer of girds was 10^-5m high; the growth rate of boundary layer grids was 1.2. Grids in the cavity between leading edge slat and main wing, at the trailing edge of leading edge slat and around trailing edge flap were locally fine. The total number of grids was about 21,000,000.

Fig. 3Schematic diagram of the grids of L1T2 high-lift airfoil

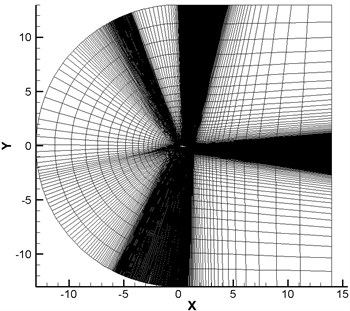
a) Computational domain of the airfoil

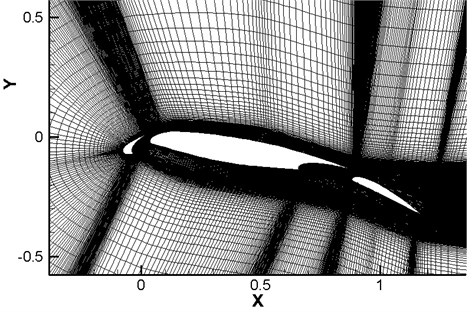
b) Grids around the airfoil

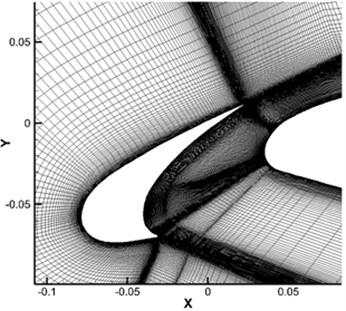
c) Grids around leading edge slat

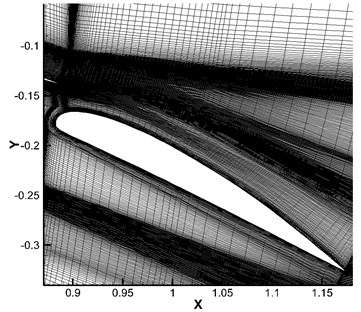
d) Grids around trailing edge flap

4. Experimental verification and analysis on the flow field of the high-lift airfoil

4.1. Experimental verification of the computational model for the flow field

The $y^{+}$ is a non-dimensional distance to the solid wall, which is used to compute turbulence model. According to $y^{+}$, the first layer grid thickness of the boundary layer could be divided. $y^{+}$ not only depends on dimensions of the first layer grid, but is also related to velocity. In general, it could be determined by experience at first. After the computation is completed, whether the value is suitable is judged according to the $y^{+}$ value. The grid will be modified if it is not suitable. Fig. 4 showed the contours for $Y^{+}$ on the upper and lower surfaces of the high-lift airfoil under Case 1. It could be seen that $Y^{+}$ was controlled between 0 and 1 for most regions of the wall surface and the value of $Y^{+}$ was between 1 and 1.5 only in some regions on the upper surface of leading edge slat and the lower surface of trailing edge flap and basically satisfied the computational requirements of LES.

Fig. 4The distribution contour of y+ on the wall surface of the high-lift airfoil (Ma= 0.3)

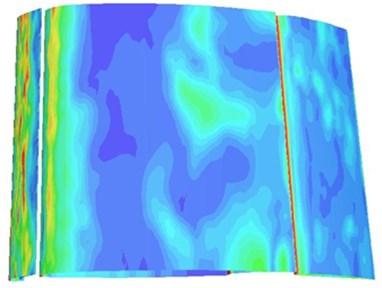
a) The distribution contour of $y^{+}$ on the upper surface

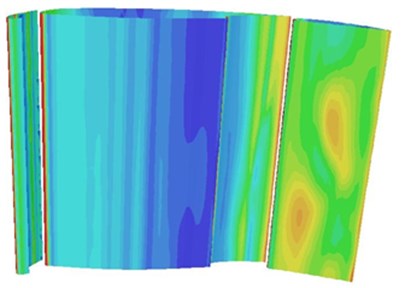
b) The distribution contour of $y^{+}$ on the lower surface

The numerical computational model of the airfoil was relatively complicated. Therefore, it was necessary to be verified by its experimental test. The experiment was conducted in a wind tunnel, as shown in Fig. 5. It was a low-velocity and straight-flow wind tunnel which had an overall length of 80 m with full-steel structure. The power of the wind tunnel was 1200 kW. The test section was a rectangular cross-section which was 8 m long, 1.6 m wide and 3 m high. The airfoil was at the center line of the wind tunnel which was 3.6 m away from the test section. The inlet Mach number was 0.3, and two ends of the airfoil were fixed. The acquisition of static pressure data on the upper and lower wall surfaces of the wind tunnel used PSI9816 intelligent pressure data system produced by an American pressure system company. The main technical indexes of the system are as follows: 512 pressure measurement channel; pressure measurement accuracy is superior to 0.05 %; every pressure passage is equipped with a micro high-accuracy sensor and a temperature sensor for digital temperature compensation. Experimental system is equipped with Lab Windows/CVI application software, develops the application platform of pressure measurement and is able to gather pressure data and graphic display in real time.

Fig. 5Wind tunnel experiment of the high-lift airfoil

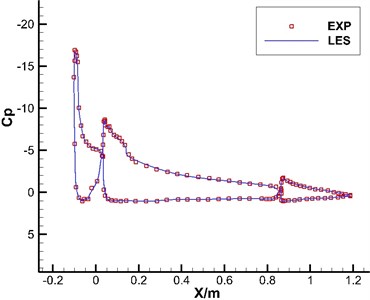
Pressure coefficients represent the change quantity between the static pressure and the dynamic pressure, and its expression is $C_p=2\left(P-P_0\right)/\rho u^2$. $P$ is surface pressures on the airfoil, $P_0$ is the reference pressure, $\rho$ is air density, and u is the flow velocity. After LES transient computation was stable, the pressure coefficients of the solid wall surface with 1000 time steps were recorded for time average. The computational result in Case 1 was shown in the solid line in Fig. 6. Scattered points in Fig. 6 were the results of pressure coefficients obtained by experimental test under the same working condition. Through comparison, it could be seen that the pressure coefficients of the solid wall surface computed by the LES in this paper were consistent with experimental results, which verified the correctness of numerical simulation for the flow field in this paper. In addition, experimental results of turbulent kinetic energy were compared with numerical simulation in this paper and published papers in order to further verify the correctness of numerical computational model and the advantage in this paper, as shown in Fig. 7.

Fig. 6Comparison of pressure coefficients between computational and experimental results

The experimental results of turbulent kinetic energy of the high-lift airfoil were shown in Fig. 7(a). The maximum turbulent kinetic energy was around the leading edge of every wing section. RNG model in reference [25] failed to predict flow separation on the surface of the airfoil and the figure did not show the region of the maximum turbulent kinetic energy. SA IDDES model in reference [26] also failed to predict large turbulent kinetic energy in the wing gap of peak wings and the region of increased turbulent kinetic energy corresponding to flow separation on the surface of the airfoil. LES model in this paper could predict large turbulent kinetic energy in the wing gap of peak wings, which was basically the same with experimental results. It indicated that the numerical prediction model in this paper had a high reliability and superiority.

4.2. Result analysis on the flow field of the airfoil

Fig. 8 displayed the pressure contour of the high-lift airfoil on the symmetry plane in Case 1 and Case 2. It could be found from the figure that obvious low-frequency and large-scale vortexes had been formed on the upper surface of flaps. Fig. 9 displayed the pressure contour on the solid surface. It could be seen that pressures had presented an obvious negative pressure characteristic on the upper surface of leading edge slat and trailing edge flap where flow was rather complicated and pressure contours had presented obvious three-dimensional effects. On the upper surface of leading edge slat and trailing edge flap, flow velocity along the chord-wise direction was high. In addition, the shape here was very complicated and there was a strong three-dimensional flow. Namely, the span-wise flow of airflow was very strong. Airflow could form highly rotary vortexes after being separated here, induce a strong zone of negative pressure below this place and improve its lift. On the upper surface of main wing, structure was very flat. Besides, airflow below the slat would pass through the cavity of slat and main wing, enter the upper surface area of main wing from top to bottom and continuously provide energy for vortexes in this place, which delayed the flow classification of main wing and achieved the effect of increasing lift. A part of airflow above main wing would also mix with separation vortexes above the flap and form more complex three-dimensional flow. As shown in Fig. 8, it could be seen from the comparison of pressure contours under different Mach numbers that the maximum value of pressures in Case 1 was more than that in Case 2 and the minimum value of pressures in Case 1 was smaller than that in Case 2 due to its high incoming Mach number.

Fig. 7Comparison of turbulent kinetic energy between experimental and numerical results

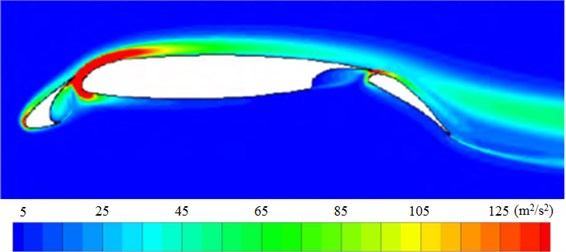
a) Experimental test result

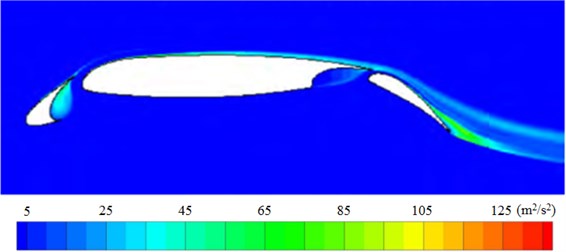
b) Numerical simulation result [25]

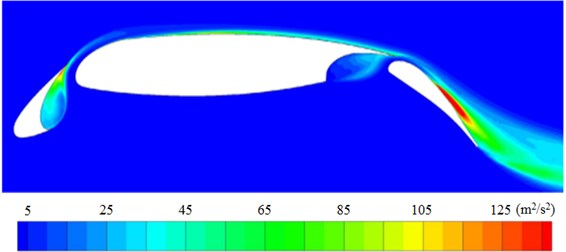
c) Numerical simulation result [26]

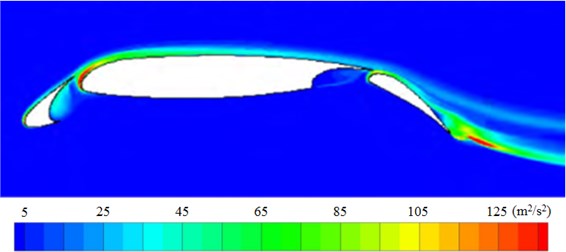
d) Numerical simulation result in this paper

Fig. 8Contours for the pressure distribution of the high-lift airfoil

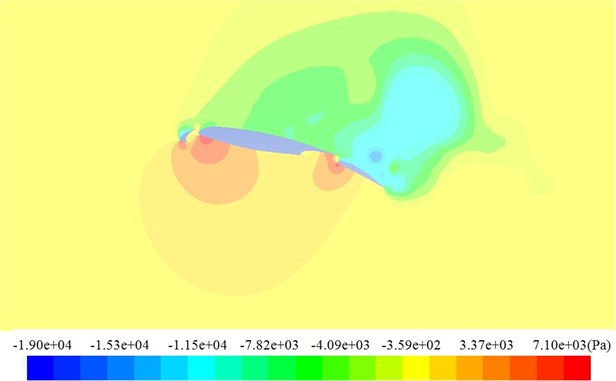
a) Mach number = 0.3

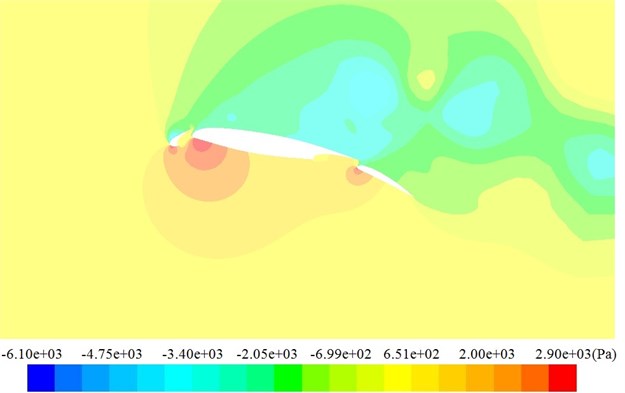
b) Mach number = 0.2

Fig. 9Contour for the pressure distribution on the solid wall surface of the high-lift airfoil (Ma= 0.3)

a) The pressure distribution on the upper surface

b) The pressure distribution on the lower surface

Fig. 10 showed the distribution contours of $x$-direction velocity of the high-lift airfoil on the symmetry plane in Case 1 and Case 2. It could be seen that there was a new boundary layer in every wing section of the high-lift airfoil; the thin turbulent boundary layer could resist adverse pressure gradient, which would not lead to the early separation of flow; every wing section had its own wake region due to the viscous flow of leading edge slat; these wake regions not only provided damping and weakened the possibility of separation for peak pressure in the downstream wing panel, but also interacted with the boundary layer in the downstream wing panel, forming a very thick mixing boundary layer and increasing the tendency of separation.

Fig. 10The distribution contours of x-direction velocity of the high-lift airfoil

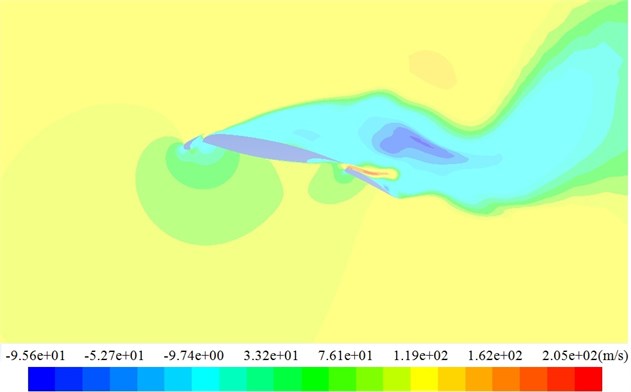
a) Mach number = 0.3

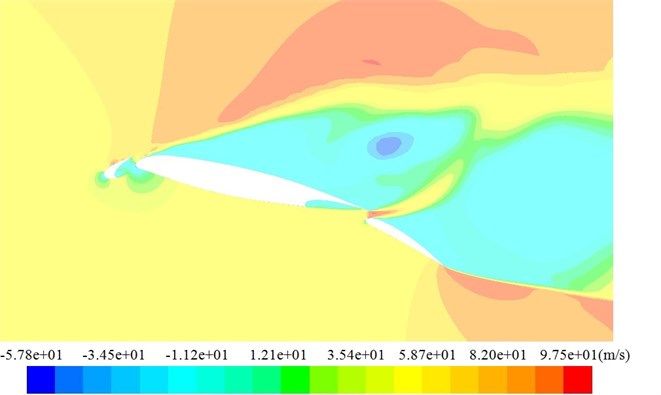
b) Mach number = 0.2

Fig. 11 displayed the equal vorticity surface rendered by pressure contour in Case 1. Vorticity values were 30, 300 and 1000 respectively. It could be seen that the flow field around leading edge slat was very complicated. The flow of trailing edge of leading edge slat on the concave surface formed a very unsteady shear layer. Rolled and discrete vortexes in the shear layer would gradually increase their sizes along the shear layer at the trialing edge of slat and form low-frequency and large-scale vortexes [27]. Potential sound sources around the flap were high-frequency and small-scale unsteady vortexes and low-frequency large-scale vortexes after the rolling-up of the free shear layer. In addition, vortexes at the trailing edge of leading edge slat would also pass through the narrow passage between slat and main wing, move backward along the upper surface of the airframe [28-33], finally mix with separation vortexes generated at the trailing edge of flaps and cause a more complex broadband noise.

Fig. 11Equal vorticity surfaces of the high-lift airfoil (Ma= 0.3)

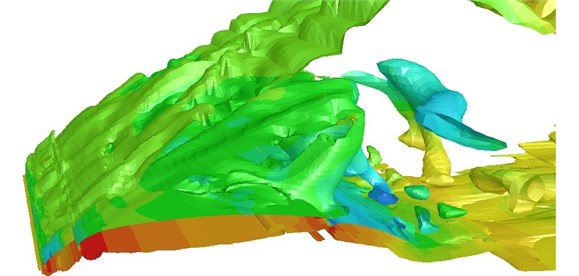
a) Vorticity value was 30

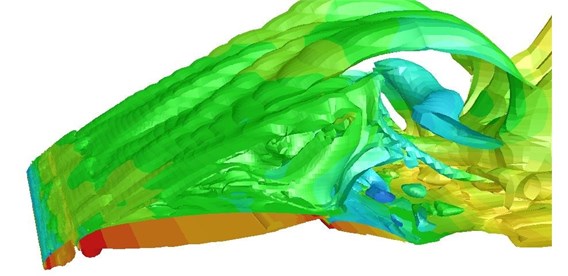
b) Vorticity value was 300

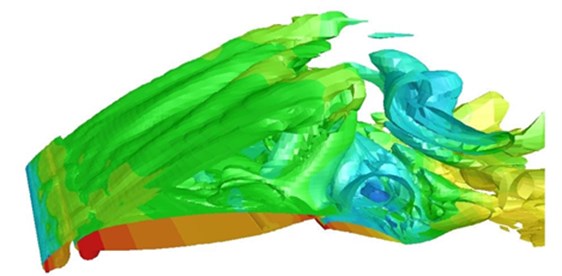
c) Vorticity value was 1000

5. Analysis on the computational results of aerodynamic noises of the high-lift airfoil

This paper took the position which was 50 m right below the airfoil as the acoustic observation point and started to record the sound source data on the integral surface after the transient flow field computed by LES was stable. Recorded flow field data included density, pressure and velocity. The integral surface of sound sources was the solid wall surface. The time step of the transient computation was $\mathrm{\Delta }t=$ 10^-4 s. The data of the integral surface in 2000 time steps was recorded. The total time for recording the data of the integral surface was $t=\mathrm{\Delta }t\cdot n=$ 0.2 s. Therefore, the resolution ratio of frequency spectrum curves of sound pressure levels after FFT was $\mathrm{\Delta }f=1/t=$ 5 Hz.

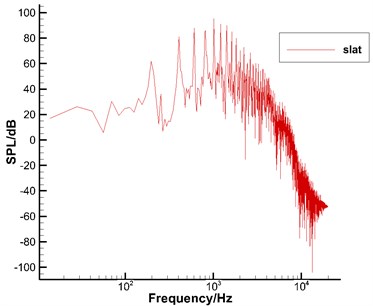
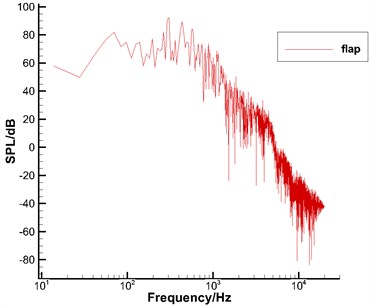
Fig. 12 displayed the computational results of noises after FFT when the integral surface of sound sources in Case 1 adopted all solid wall surfaces, leading edge slat and trailing edge flap to integrate. It could be seen from Fig. 12(a) that the overall noise presented broadband characteristics and its sound energy was mainly within 0-5000 Hz. It could be seen from Fig. 12(b) that flow on the concave surface of slats formed a very unsteady shear layer; rolled and discrete vortexes in the shear layer would gradually increase their sizes along the shear layer at the trailing edge of slats and form low-frequency large-scale vortexes and high-frequency small-scale vortexes. As a result, certain broadband characteristics would be presented like the overall noise in Fig. 12(a). From Fig. 12(c), it could be seen that the trailing edge flaps presented very obvious low frequency characteristics and sound energy was mainly within 0-300 Hz. It was because the rolling-up of the free shear layer on the concave surface between flaps and the main body of airfoils as well as the flap would cause high-frequency small-scale unsteady vortexes and low-frequency large-scale vortexes. Moreover, low-frequency and large-scale vortexes were the main part of energy.

Fig. 12Frequency spectrum of sound pressure levels of the high-lift airfoil (Ma= 0.3)

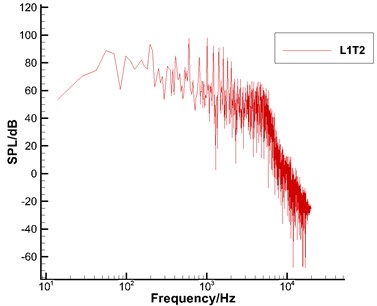
a) All wing sections

b) The leading edge slat

c) The trailing edge flap

Fig. 13 displayed the frequency spectrum of 1/3 octave in Case 1, took all solid wall surfaces, leading edge slat and trailing edge flap as the integral surfaces and used logarithmic coordinates to express frequency. Here, high and low frequency characteristics of all wing sections could be seen more obviously. L1T2 presented a more obvious broadband characteristic on the whole. The peak value of frequency spectrums of leading edge slat was mainly in two positions. Around 200 Hz, one position was mainly composed of low-frequency small-scale vortexes at the shear layer and cavity of trailing edge of slat. The other position was around 1000 Hz. In addition, the sound pressure level of peak value in this position was the maximum. This position was mainly composed of high-frequency small-scale vortexes which gradually rolled up at the shear layer of trailing edge of slat. The frequency spectrum of trailing edge flap was mainly within 300 Hz. In addition, the frequency spectrum had such a peak value.

Fig. 13Frequency spectrum of 1/3 octave in all wing sections of the high-lift airfoil (Ma= 0.3)

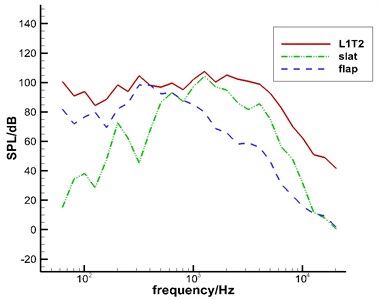
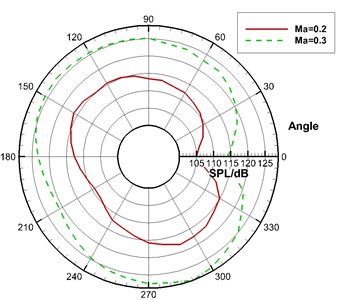
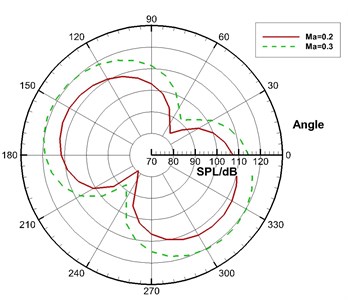
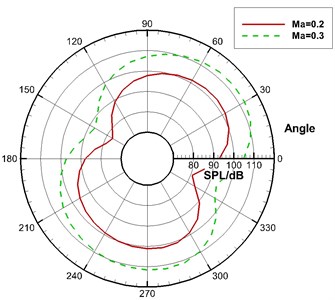
Fig. 14The acoustic directivity in all wing sections of the high-lift airfoil (Ma= 0.3)

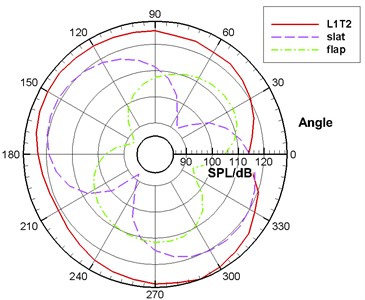
Fig. 15The directivity of the high-lift airfoil under different Mach numbers

a) All wing sections

b) Leading edge slat

c) Trailing edge flap

Fig. 14 displayed the directivity diagram for the far-field acoustic in Case 1. All solid wall surfaces, leading edge slat and trailing edge flap were taken as the integral surfaces. It could be seen that the sound pressure level of leading edge slat in the direction vertical to its chord was the largest and about 120 dB. Trailing edge flap was similar to the slat. Similarly, the sound pressure level of trailing edge flap in the direction vertical to its chord was the largest and around 110 dB. In addition, it could also be seen from Fig. 14 that leading edge slat and trailing edge flap presented a very obvious dipole characteristic and L1T2 also showed certain dipole characteristics on the whole.

Fig. 15 displayed the acoustic directivity under different Mach numbers. It could be seen that the sound pressure level in Case 1 was obviously higher than that in Case 2. From the previous analysis, it could be seen that the main noise of the high-lift airfoil was from dipole noise sources and the intensity of dipole noises was in direct proportion to the 6th power of incoming Mach number. According to this theory, the difference between the sound pressure levels in Case 1 and Case 2 was about 20·log(0.3/0.2)³ ≈ 10.56 dB. It could be seen from Fig. 15 that the difference between the sound pressure levels in Case 1 and Case 2 was only about 10 dB, which was consistent with the results of theoretical computation. It proved that the far-field aerodynamic noise of the high-lift airfoil computed in this paper satisfied the noise characteristics of dipole from another perspective and again verified the effectiveness of numerical simulation results in this paper.

6. Conclusions

1) The correctness and superiority of the numerical model in this paper were verified through comparing the pressure coefficient and turbulent kinetic energy between experimental test and numerical simulation.

2) The flow on the concave surface of leading edge slat formed a very unsteady shear layer. Rolled and discrete vortexes in the shear layer would gradually increase their sizes along the shear layer of trailing edge of slat and form low-frequency large-scale vortexes as well as high-frequency small-scale vortexes.

3) On the concave surface between flaps and the main body of airfoils as well as the flap, the rolling-up of the free shear layer would cause high-frequency small-scale unsteady vortexes and low-frequency large-scale vortexes. However, main sound sources were low-frequency large-scale vortexes. Besides, vortexes at the trialing edge of leading edge slat would pass through the narrow passage between slat and main wing, move backward along the upper surface of airframe, finally mix with separation vortexes generated at the trailing edge of flaps and form a more complex broadband noise.

4) The computed high-lift airfoil presented a very obvious broadband characteristic on the whole. The peak value of frequency spectrums of leading edge slat was mainly in two positions. One position was at 200 Hz, and the other position was around 1000 Hz. Trailing edge flap presented a very obvious low frequency characteristic. The frequency spectrum of sound pressure levels only had one obvious peak value which was mainly around 300 Hz.

5) The acoustic directivity of leading edge slat and trailing edge flap presented an obvious dipole characteristic. In addition, sound pressure levels of leading edge slat and trailing edge flap in the direction vertical to chords were the largest. This paper proved that the computational results satisfied the 6th power rule of dipole through comparing the acoustic directivity under different incoming Mach numbers.