Tooth surface friction and its influence on dynamic transmission error of double power input transmission system

1. Introduction

For a helicopter drive system with planetary gear transmission, the speed ratio of the planetary gear is restricted by its structure and strength. At the same time, the transmission efficiency of planetary gear is decreased with the increase of the speed ratio, what is not desirable to the helicopter transmission system. Therefore, in order to meet the power-weight ratio, transmission efficiency and reliability requirements, as far as possible to reduce the weight and volume of the helicopter transmission system, the ratio of planetary gear should not be too large.

At present, single helicopter engine power has reached 2000-3000 kW with the speed from 20000 to 30000 r/min or so. As the main rotor speed is generally around 200 rpm, the transmission ratio of the main reducer is larger, and the speed range is wider. For the sake of the design requirements of the total transmission ratio of the main reducer, if the planetary gear is still used, at least two stage planetary gears are required for the drive system due to the scope of control of the planetary gear. Hence, the structure of the main reducer will be more complex, and the weight will increase affecting the performance of the transmission system.

Recently, several scholars proposed a novel gear train arrangement, known as a split torque or split-path arrangement. The final stage of the main gearbox with split torque transmission is expected to get the advantages of sharing the torque among multiple pinions, the same as it is done in a traditional planetary stage, while obtaining a larger reduction ratio than possible for a planetary design. Compared with the conventional transmission with a planetary gear stage, white [1-3] has advocated the benefits for a 3600 hp split torque transmission, stating that these designs offered the following advantages over the traditional arrangements:

(a) high speed reduction ratio at the final stage, and it is very beneficial for reducing the weight of the drive system,

(b) fewer gears and bearings, and increased reliability of separate drive paths,

(c) lower energy losses, and lower noise.

Clearly, a split torque design can provide significant advantages over the commonly used planetary design, and contributes to the realization of the above requirements.

Around this split torque transmission system, some significant theoretical and experimental studies regarding load sharing and dynamic characteristics have been made and proposed. In order to eliminate the special load-sharing devices and to achieve load sharing properties in the Comanche and future rotorcraft, Krantz [4, 5] proposed a new method. He defined a clocking angle as the design variable of the split path gearboxes. The clocking angle can be adjusted to split a design load equally between two power paths. The method has higher requirements to manufacturing and installation errors. Cocking [6] and Smirnov [7] described split-path designs, which featured quill shafts to minimize the torque loading differences between two parallel power pathways. At present, this method using an elastic shaft to realize uniform load was further applied to other transmission systems [8-10].

The dynamic characteristics of the transmission system were one of the research interests. Scholars also analyzed the dynamic response of split torque transmissions. Majid [11] and Krantz [12, 13] investigated the vibration and dynamic characteristics of a split path gearbox, and the results related to three variables, shaft angle, mesh stiffness and compound shaft stiffness were presented. The results show that most of the natural vibration frequencies are not significantly influenced by changes of the shaft angle, and the mesh phasing and the stiffness of shafts strongly influenced the level of vibration energy. Yang [14] and Du [15] studied the characteristics of torsional vibration of split torque transmissions. Zhang [16] obtained the law of error influence on the load sharing characteristics, and the functional relationship between the error and the mesh load factor. Based on the conditions of deflection compatibility of torsional angle, Dong [17, 18] analyzed the load-sharing coefficient of the system and the influences of the installation and manufacturing errors of each component on the power split. Zhao [19] presented a dynamics model for the parallel shaft torque transmission system, and the influence of the dynamic load characteristics, as well as the components of manufacturing and installation errors on the non-uniform coefficient of transmission system load were analyzed. The calculation results show that, when the effect of support stiffness is not considered, the load sharing property of parallel shaft torque transmission system is improved very obviously by floating of input shaft. Gui [20, 21] discussed the impact of torsional stiffness and backlash on dynamic and load sharing characteristics of the nonlinear cylindrical gear split-torque transmission system. A dynamic model of split torque transmission is established with the consideration of the time-varying friction coefficient and time-varying mesh stiffness. The experimental dynamic load sharing coefficients are obtained in a good agreement with the theoretical analysis [22].

As it can be seen from the above literatures, although a lot of researches related to the split torque transmission system were carried out, and many new models considering variable parameters were proposed as well, it should be noted that there was very few related studies on the tooth flank friction regarding friction stiffness and its conference on the dynamic transmission error, and most of them were limited to a single power input and two-stage transmission. The main purpose of this paper is to build a new model including the friction stiffness and friction torque coefficient, and to make a qualitative analysis of friction influence on the dynamic transmission error by solving differential equations using the Fourier series method. The primary concerns of the paper are (i) bending-torsional coupled dynamic equations with a double power input; (ii) friction stiffness and friction torque coefficient; (iii) influence on the transmission error of friction.

2. Dynamic model of split torque transmission system

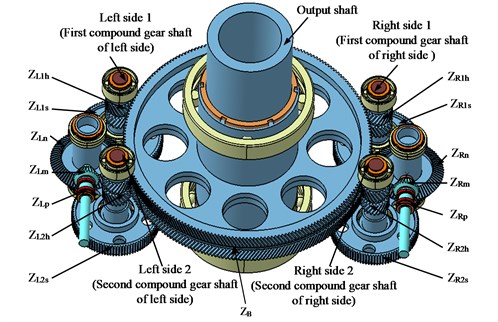
The schematic illustration of the split torque transmission in a helicopter main gearbox powered by two engines is shown in Fig. 1. It can be seen from the figure that the system has two power inputs, and is composed of three-stage drives. The structure and components of each transfer path are the same, and the components of two branch transmission subsystems are defined by subscripts $L$ and $R$, respectively. In the first stage gear drive, the input bevel gear $Z_{im}$ meshes with $Z_{in}$ ($i=L$, $R$). For the convenience of narration, the second stage is defined as the split torque stage. In this stage, the pinion $Z_{ip}$ meshes with two gears simultaneously, that is $Z_{i1s}$ and $Z_{i2s}$. The final stage is the torque confluence stage, and gears of $Z_{i1h}$ and $Z_{i2h}$ all mesh with output gear $Z_B$ at the same time.

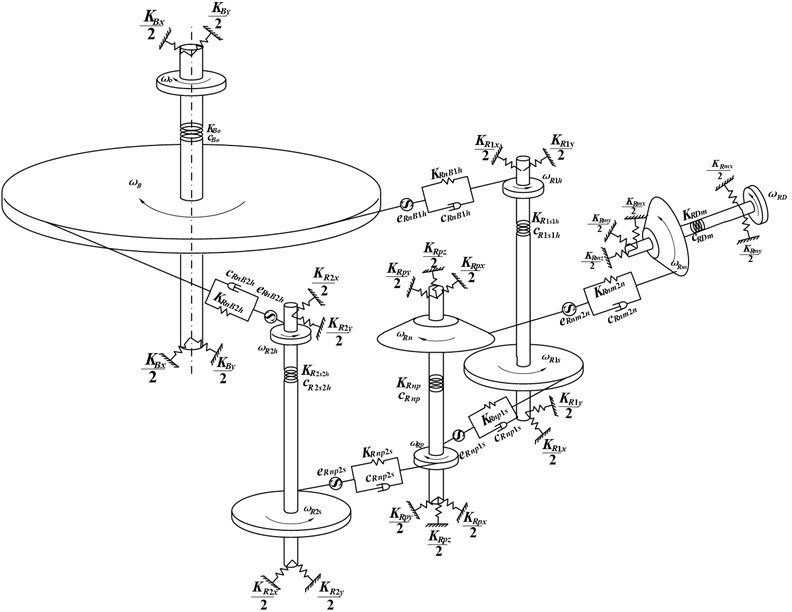
Fig. 2 shows a lumped-parameter dynamic model of this drive system, in which the moment of inertia of input and output components is included. Because the gear train arrangement is symmetrical, only a half of the edges is drawn in order to express the graph clearly. The gear mesh interface and the shaft are modeled as a spring-damper system, and the bearing is simulated with a spring. $K$, $c$ and $e$ with appropriate subscript represent the stiffness, damping and transmission error respectively. The component of input shaft has five degrees of freedom: transverse motions in the $x$-axis and $y$-axis, axial motion in the $z$-axis, and torsional angle of $Z_{Rm}$ and input torsional angle ${\phi }_{RD}$. The component of shaft where $Z_{Rn}$ mounts on also has five degrees of freedom: transverse motions in the $x$-axis and $y$-axis, axial motion in the $z$-axis, and torsional angles of $Z_{Rn}$ and $Z_{Rp}$. The component of shaft where $Z_{Rjh}$ ($j=$1, 2) mounts on has four degrees of freedom: transverse motions in the $x$-axis and $y$-axis, and torsional angle of $Z_{Rjh}$ and $Z_{Rjs}$. The output shaft component also has four degrees of freedom: transverse motions in the $x$-axis and $y$-axis, and torsional angle of $Z_B$ and output torsional angle ${\phi }_o$. In this model, we have ignored the effects of motors, housing, coupling, and other practical phenomena such as backlash. Therefore, the whole model can be described by the total of 40 freedom degrees, and generalized displacement vector $\mathbf{Y}$ is given by:

where ${\phi }_{in}$, ${\phi }_{im}$, ${\phi }_{ip}$, ${\phi }_{ijs}$, ${\phi }_{ijh}$ and ${\phi }_B$ represent the angular displacements of gears respectively. Displacements of the input shaft, split torque shaft, dual-gear shaft and output shaft are expressed by $X_{inm}$ and $Y_{inm}$, $X_{inp}$ and $Y_{inp}$, $X_{ij}$ and $Y_{ij}$, $X_B$ and $Y_B$, respectively. $Z_{imn}$and $Z_{inp}$ are the axial displacements of the input shaft and the split torque shaft.

Fig. 1Schematic illustration of split torque transmission system

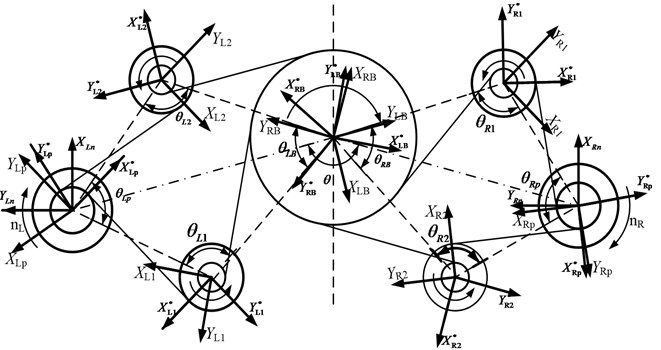
In order to facilitate the analysis of the dynamic system characteristics, the generalized coordinate system and local coordinate system are used, as shown in Fig. 3. In this figure, reference coordinate frames with superscript (*) are local, and the direction of $Y^{\mathrm{*}}$ and $Y$ is coincident with the line of action for each particular meshing gears. ${\theta }_{ip}$, ${\theta }_{i1}$, ${\theta }_{i2}$, ${\theta }_{iB}$ and $\theta$ are the angles between the center line of the gears. The pressure angle of gears is expressed by $\alpha$ with the corresponding subscript. According to the geometric relations shown in the graph, the transformation relation between the generalized coordinates and local coordinates can be written as:

where ${\theta }_{Rn}$ and ${\theta }_{Ln}$ can be expressed as $({\alpha }_{Rnp1s}+{\theta }_{RP}/2-\theta /2-\pi /2)$ and $({\alpha }_{Lnp1s}+{\theta }_{LP}/2-\theta /2-\pi /2)$. ${\theta }_{R1}^{\text{'}}$, ${\theta }_{R2}^{\text{'}}$, ${\theta }_{L1}^{\text{'}}$ and ${\theta }_{L2}^{\text{'}}$ can be expressed as $({\theta }_{R1}-{\alpha }_{RnB1h}-{\alpha }_{Rnp1s})$, $({\theta }_{R2}-{\alpha }_{RnB2h}-{\alpha }_{Rnp2s})$, $({\theta }_{L1}+{\alpha }_{LnR1h}-{\alpha }_{Lnp1s})$ and $({\theta }_{L2}+{\alpha }_{LnR1h}+{\alpha }_{Lnp1s})$.

Fig. 2Dynamic model of transmission system

The displacements specified in these coordinate frames are described in only the global reference frame by transforming the local coordinate via rotational coordinate transformations, and will be used for a $Y_{LB}$ numerical calculation. For the unity of the symbols, let $X_B$ be used instead of $X_{LB}$, and $Y_B$ – instead of $Y_{LB}$.

Fig. 3Relationship of local and generalized system coordinates

3. Dynamic equations of split torque transmission system

3.1. Relationship between angular displacement and linear displacement

The relative displacement of the meshing gear pair in the direction of meshing line is defined as the dynamic transmission error. According to the geometrical relationships shown in Fig. 3, for split torque stages and torque confluence stages gears, the relationship displacement of the meshing line and the twist angle can be expressed as:

3

$\left\{\begin{array}{l}{Y}_{inp1s}=(-Y_{ip}+r_{ibp}{\phi }_{ip})-(Y_{i1}^{\mathrm{*}}+r_{ib1s}{\phi }_{i1s})-e_{inp1s},\\ Y_{inp2s}=(-Y_{ip}^{\mathrm{*}}+r_{ibp}{\phi }_{ip})-(Y_{i2}+r_{ib2s}{\phi }_{i2s})-e_{inp2s},\\ Y_{inB1h}=(-Y_{i1}+r_{ib1h}{\phi }_{i1h})-(Y_{iB}^{\mathrm{*}}+r_{bB}{\phi }_B)-e_{inB1h},\\ Y_{inB2h}=(-Y_{i2}^{\mathrm{*}}+r_{ib2h}{\phi }_{i2h})-(Y_{iB}+r_{bB}{\phi }_B)-e_{inB2h},\end{array}\right.$

where $Y_{inp1s}$, $Y_{inp2s}$, $Y_{inB1h}$ and $Y_{inB2h}$ respectively express the relative displacement of $Z_{ip}$ and $Z_{i1s}$, $Z_{ip}$ and $Z_{i2s}$, $Z_B$ and $Z_{i1h}$, $Z_B$ and $Z_{i2h}$ along the direction of the meshing line. $r_{ibp}$, $r_{ib1s}$, $r_{ib2s}$, $r_{ib1h}$, $r_{ib2h}$ and $r_{bB}$ respectively express the base circle radius of $Z_{ip}$, $Z_{i1s}$, $Z_{i2s}$, $Z_{i1h}$, $Z_{i2h}$ and $Z_B$.

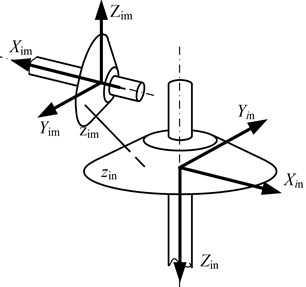
According to the coordinates of the input stage bevel gears shown in Fig. 4, the relation between the dynamic relative displacement $Y_{inm2n}$ along the meshing line and the rotation angle displacement of the bevel gears can be expressed as:

4

$Y_{inm2n}=(-X_{im}-X_{in})P_{Xmn}+(Z_{im}+Z_{in})P_{Zmn}$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+(Y_{im}-{\phi }_{im}{r}_{ipm}+Y_{in}+{\phi }_{in}{r}_{ipn})P_{Ymn}-e_{inm2n},$

where $r_{ipm}$ and $r_{ipn}$ express the radius of mesh points of bevel gears. Calculation parameters $P_{Xmn}$, $P_{Ymn}$ and $P_{Zmn}$ can be expressed as:

5

$\left\{\begin{array}{l}{P}_{Xmn}=\mathrm{s}\mathrm{i}\mathrm{n}{\delta }_{in}\mathrm{s}\mathrm{i}\mathrm{n}{\beta }_{in}\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_{in}+\mathrm{c}\mathrm{o}\mathrm{s}{\delta }_{in}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_{in},\\ P_{Ymn}=\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_{in}\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_{in},\\ P_{Zmn}=\mathrm{c}\mathrm{o}\mathrm{s}{\delta }_{in}\mathrm{s}\mathrm{i}\mathrm{n}{\beta }_{in}\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_{in}-\mathrm{s}\mathrm{i}\mathrm{n}{\delta }_{in}\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_{in},\end{array}\right.$

where ${\alpha }_{in}$ is the normal pressure angle of $Z_{in}$, ${\beta }_{in}$ is the helix angle, and ${\delta }_{in}$ is the pitch cone angle.

Fig. 4Input stage bevel gear coordinate system

The relative angular shaft displacement is transformed into the torsion line displacement, and it can be represented as:

6

$\left\{\begin{array}{l}{Y}_{iDm}=r_{iDm}({\phi }_{iD}-{\phi }_{im}),\\ Y_{inp}=r_{inp}({\phi }_{in}-{\phi }_{ip}),\\ Y_{i1s1h}=r_{i1s1h}({\phi }_{i1s}-{\phi }_{i1h}),\\ Y_{i2s2h}=r_{i2s2h}({\phi }_{i2s}-{\phi }_{i2h}),\\ Y_{Bo}=r_{Bo}({\phi }_B-{\phi }_o),\end{array}\right.$

where $Y_{iDm}$, $Y_{inp}$, $Y_{i1s1h}$, $Y_{i2s2h}$ and $Y_{Bo}$respectively express the torsion linear displacement of input shaft, split torque shaft, dual-gear shaft 1, dual-gear shaft 2 and output shaft. $r_{iDm}$, $r_{inp}$, $r_{i1s1h}$, $r_{i2s2h}$ and $r_{Bo}$ respectively express the equivalent radius of the shafts.

4. Friction stiffness and friction torque coefficient

From Eq. (7) and Eq. (11), it can be seen that the friction and friction torque of gear pair are related to the factors such as the friction coefficient, meshing stiffness, friction arm and so on. The friction coefficient, mesh stiffness and friction arm are periodic functions with respect to time. In order to facilitate the subsequent calculation and analysis, the product of time-varying friction coefficient and time-varying meshing stiffness of gear pair is defined as the friction stiffness $Kf$, and the product of time-varying friction stiffness and friction arm of gear pair is defined as the friction torque coefficient $KTf$. They can be described as:

where ${\lambda }_{Kf}\left(t\right)$ is friction direction parameter. It is positive when the friction is in the positive direction of the coordinate system, and it will change at the pitch point. $r\left(t\right)$ is the arm of friction.

4.1. Calculation of friction stiffness and friction torque coefficient of spur gear

Fig. 5(a) shows a schematic diagram of the spur gear meshing. The length of contact line $KK\mathrm{\text{'}}$ remains unchanged and parallel to the axis when tooth contact begins and ends along the line of action. In a meshing period of gear teeth, the time-varying friction stiffness $K{f}_i\left(t\right)$ and friction torque coefficient, $KT{f}_{1i}\left(t\right)$ and $KT{f}_{2i}\left(t\right)$, can be expressed as:

16a

$\left\{\begin{array}{l}K{f}_i\left(t\right)={\lambda }_i\left(t\right){\mu }_i\left(t\right)k_{oi}l,\\ KT{f}_{1i}\left(t\right)={\lambda }_{1i}\left(t\right){\mu }_i\left(t\right)k_{oi}l{R}_{1i}\left(t\right),\\ KT{f}_{2i}\left(t\right)={\lambda }_{2i}\left(t\right){\mu }_i\left(t\right)k_{oi}l{R}_{2i}\left(t\right),\end{array}\right.$

where $k_{oi}$ is meshing stiffness of the unit contact line, $l$ the length of contact line. The total friction stiffness and friction torque coefficient of all engagement teeth are obtained by the superposition of the friction stiffness and the friction torque coefficient in a meshing period, which can be expressed as follows:

16b

$\left\{\begin{array}{l}Kf\left(t\right)=\sum _{i}K{f}_i\left(t\right),\\ KT{f}_1\left(t\right)=\sum _{i}KT{f}_{1i}\left(t\right),\\ KT{f}_2\left(t\right)=\sum _{i}KT{f}_{2i}\left(t\right).\end{array}\right.$

Fig. 5Engagement process of cylindrical gear

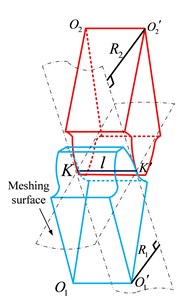
a) Spur gear

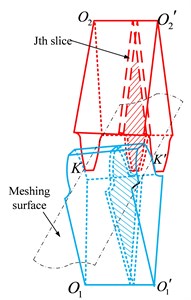
b) Helical gear

5. Tooth surface friction and dynamic transmission error

To avoid the interference of gear meshing, the tooth matching formula is derived. Based on the power transmission of a helicopter, taking the minimum volume or the least weight as the target, the main transmission parameters shown in Table 2 are obtained by optimized designing. There are not good theoretical methods for solving the differential equations, because of the characteristics of multifactor coupling, time-varying and many degrees of freedom. Thus, the Fourier series method is used to solve the equations by transforming the time varying system into a linear time invariant system. Time-varying parameters are divided into a not-time-varying mean value part and time-varying volatility part with neglecting high-order quantities. After finishing, the equations are transformed into a linear constant system. With the gear frequency as the fundamental frequency, the excitation term of meshing stiffness fluctuation and the friction excitation are expanded into Fourier series by selecting the first few orders of frequency. Besides, error excitation is also expanded into Fourier series with the shaft frequency as the fundamental frequency. The total system response can be obtained after the superposition of the each order excitation response. When the Fourier method is used to solve the time history of vibration, the vibration spectrum is also obtained.

5.1. Analysis of friction stiffness and coefficient of friction torque of spur gear

The calculation results of friction stiffness of spur gear are shown in Fig. 6. In the meshing process, the friction stiffness decreases gradually from the entry to pitch point. However, the value gradually increases in the reverse direction when the meshing point passes through the pitch point. That is because the value of relative sliding velocity and friction coefficient become larger and larger when the meshing point is far away from the pitch point, and the direction of relative sliding velocity between contact tooth flanks is changed. The results show that the friction stiffness in the entering meshing area is larger than that of the exiting meshing area.

Fig. 6Friction stiffness of spur gear

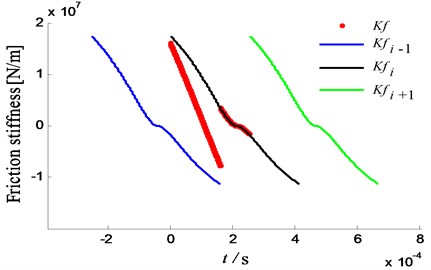
The change law of friction torque coefficient and friction stiffness is the same, as shown in Fig. 7. This result demonstrates that the friction torque of the driving gear is the same as the direction of driving torque, and the friction torque of the driven gear is the same as that of the load torque in the engaging process from the start point to the pitch point. However, the conclusion is opposite when the meshing point passes through the pitch point. In the whole meshing process, the absolute values of friction torque coefficient of the driving gear are maximal at the end point of engagement, and the largest values of that for the driven gear are located at the starting point of engagement.

Fig. 7Friction torque coefficient of spur gear

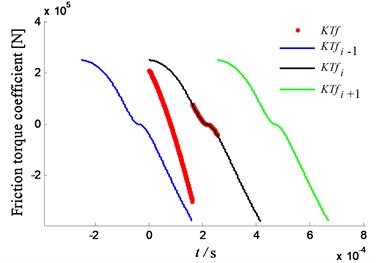
a) Friction torque coefficient of driving gear

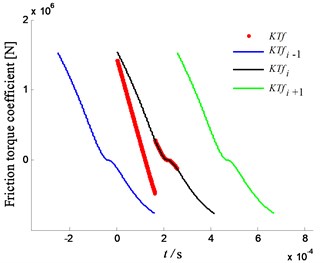
b) Friction torque coefficient of driven gear

5.2. Analysis of friction stiffness and coefficient of friction torque of herringbone gear

The calculation results of friction stiffness of herringbone gear (double helical gear) are shown in Fig. 8. Compared to a single helical gear, the friction stiffness curve changes gently, and the amplitude of the alternating component is small. Furthermore, compared with a spur gear, the stiffness curve is continuous without mutations, and the direction of friction stiffness is constant. Hence the resultant friction force direction is not changed for a herringbone gear train.

Fig. 8Friction stiffness of herringbone gear

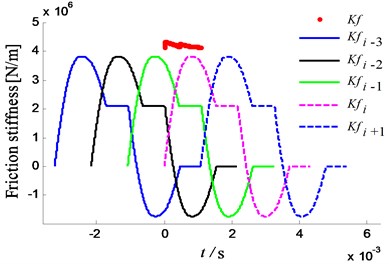
Fig. 9Friction torque coefficient of herringbone gear

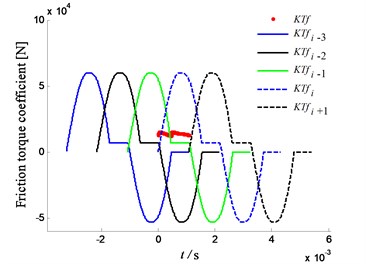
a) Friction torque coefficient of driving gear

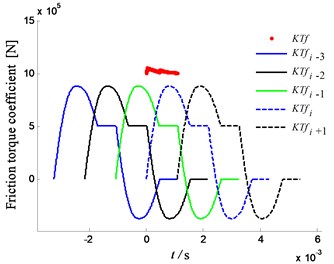
b) Friction torque coefficient of driven gear

The change law of friction torque coefficient and friction stiffness is the same, as shown in Fig. 8. In addition, the amplitude of driving gear is smaller than that of the driven gear, as shown in Fig. 9. Compared with spur gear, the amplitude is small, and the direction of friction torque coefficient is unchanged.

Fig. 10Transmission error along YRnp1s and contribution proportion of harmonic order

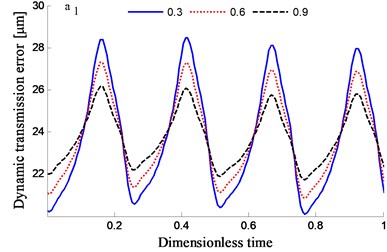
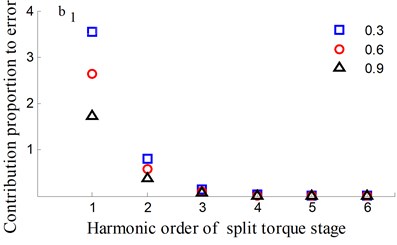
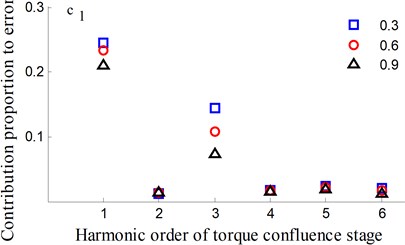
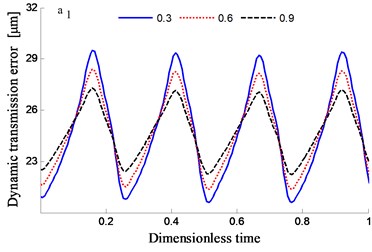
Fig. 11Transmission error along YRnp2s and contribution proportion of harmonic order

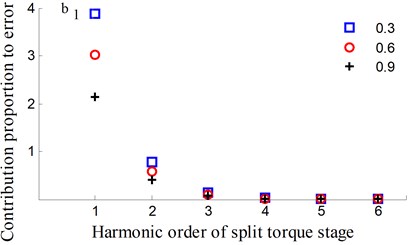
5.3. Analysis of dynamic transmission error

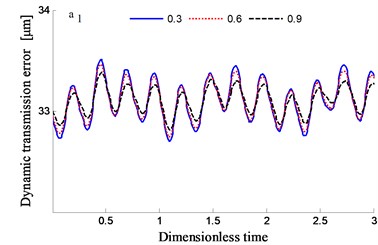
In order to study the influence of tooth flank roughness on the dynamic transmission errors of the system, a few of root mean squares of the roughness is analyzed to have 0.3, 0.6 and 0.9, respectively.

The time-frequency domain graphs of the dynamic transmission error along the line of action are shown in Figs. 10-17. After comparing the time domain diagram, we gain the results that the amplitude of the dynamic transmission error decreases with the increase of tooth surface roughness, and the trend is more obvious for the spur gear. Moreover, research results show that the friction and friction torque of the tooth flank increase with the increase of roughness. Due to the difference of friction torque coefficient, the gear meshing force decreases when the direction of friction and friction torque is opposite to the meshing force.

Fig. 12Transmission error along YRnB1h and contribution proportion of harmonic order

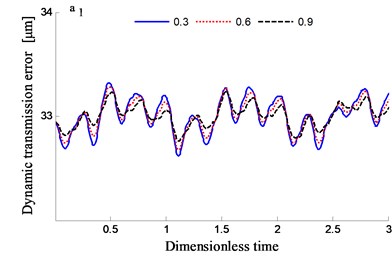
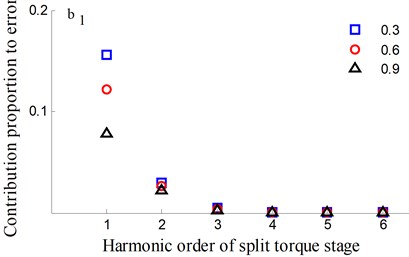
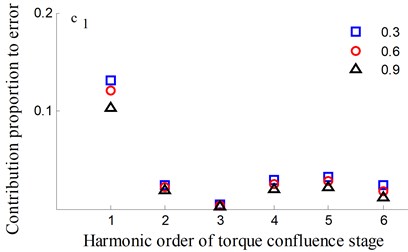
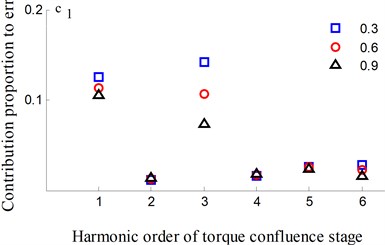
Fig. 13Transmission error along YRnB2h and contribution proportion of harmonic order

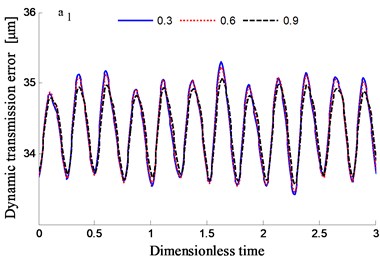
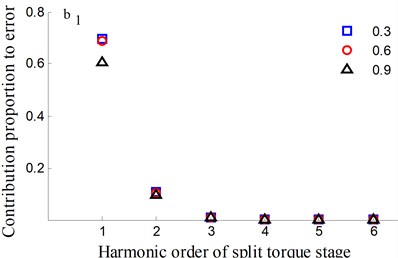
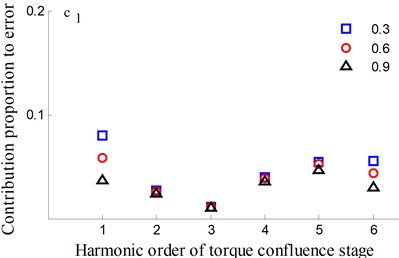
Fig. 14Transmission error along YLnp1s and contribution proportion of harmonic order

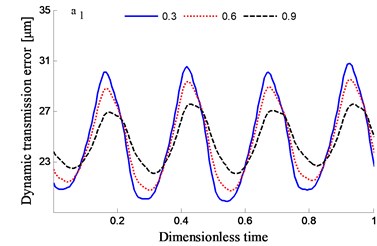
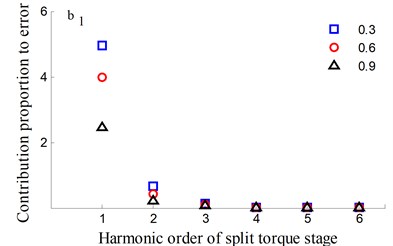
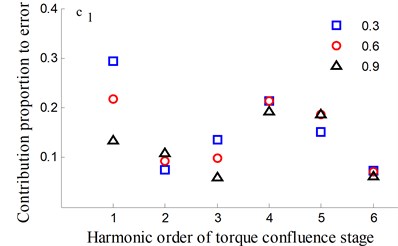
Fig. 15Transmission error along YLnp2s and contribution proportion of harmonic order

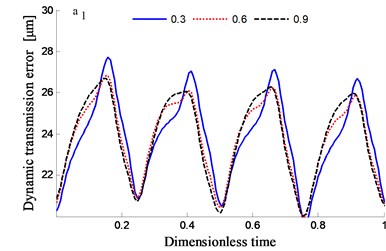
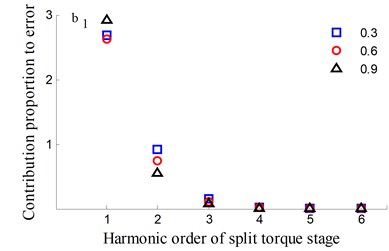
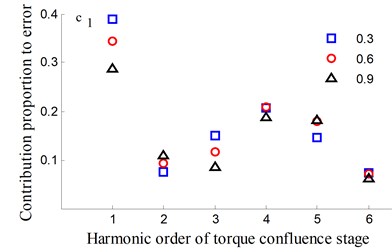
It could be observed from the frequency domain diagram that the influence of harmonic order of spur gear on the dynamic transmission error of each branch is mainly concentrated in the first and second orders. Besides, the harmonic order of herringbone gears also has some influence. With the increase of tooth surface roughness, the amplitude has a reduction in a different degree. Furthermore, the effects of harmonic order of split torque stages are significantly greater than those of torque confluence stages, as it can be seen from the error-contribution ratio. In addition, although the geometry of the drive system is symmetrical, and the torsional stiffness and support stiffness of the shaft are equal, the gear train force is asymmetric. Thus, the gear center will produce lateral micro-displacement, as a result the rotational deformations of the gears are different, and the power of two branches is out of balance. Due to large stiffness of torque confluence stages, the impact of tooth surface friction is mainly reflected in the split torque stages.

Fig. 16Transmission error along YLnB1h and contribution proportion of harmonic order

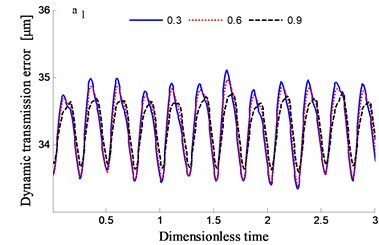
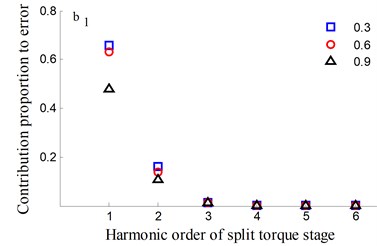
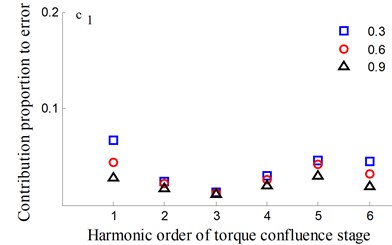
Fig. 17Transmission error along YLnB2h and contribution proportion of harmonic order

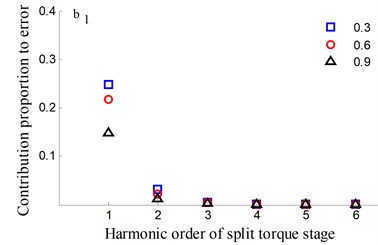
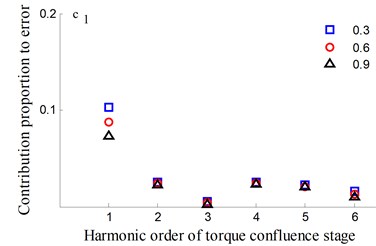
6. Conclusions

Based on the concentrated parameter theory, considering the influence of time-varying friction coefficient, time-varying meshing stiffness and the integrated error, a three-dimensional dynamic model with 41 degrees of freedom is developed, including the flexional, torsional and axial motions. According to the meshing characteristics of spur gears and helical gears, the calculation formulas of time-varying friction stiffness and friction torque coefficient are derived. The dynamic equations are solved by the Fourier series method, and the dynamic characteristics and the change law of system friction characteristics are obtained. Compared to a single helical gear, the friction stiffness curve of herringbone gear changes gently without mutations, and the direction is constant what makes the resultant friction force direction to be unchanged. The tooth surface roughness has a certain influence on the dynamic transmission error. Due to the asymmetry of the force caused by the structure and its deformation, as well as larger stiffness of torque confluence stages, the impact trend is more obvious for split torque stages. The first and second harmonic order frequencies of the split torque stage gears have an important influence on the dynamic transmission errors.