Abstract
This paper investigates the characteristics of high-damping rubber bearings (HDRBs) through various prototype tests. The characteristics were dependent on the displacements, number of load cycles, frequencies, vertical pressure, temperature, shear deformation capability, and vertical stiffness. The prototype tests showed that the displacement was the most influential factor on the characteristics of the HDRB. The effective stiffness and equivalent damping of the HDRB decreased with the displacement and increased with the frequency. The effective stiffness decreased at higher vertical pressure, while the equivalent damping increased. The equivalent damping was more dependent on the vertical pressure than the effective stiffness. The results show that careful examination is required to design the effective stiffness and equivalent damping ratio while considering the dependencies of the design displacement and excitation velocity.
1. Introduction
South Korea is far away from plate boundaries where seismic activity is frequent and has been recognized as a relatively safe nation for earthquakes. However, the frequency of earthquakes has increased in recent years, and the PyeongChang earthquake reached 4.5 on the Richter scale. As a result, seismic-related technologies and measures have been developed to minimize earthquake damage and protect life and property.
To develop seismic technologies, a number of studies have been conducted on the design and installation of earthquake isolation systems for buildings and bridges to alleviate the seismic force and minimize earthquake damage. Such efforts include installing earthquake isolation bearings on structures such as bridges or storage tanks for liquefied natural gas. Increased use of earthquake isolation bearings is expected to ensure the seismic performance and design of bridges and structures.
Earthquake isolation devices have been widely used for bridges since regulations on the designs of earthquake isolation bridges were established in the Seismic Design section of the recently revised Korean Highway Bridge Design Code (2005). In other words, (Aiken et al., 1992) and (Takayama M. et al., 1995) have applied seismic isolation to a large number of bridge structures [1, 2]. Increasing the natural cycle of bridges can decrease the seismic force and help absorb seismic energy. (Robinson W.H. et al., 1982) and (Mineoh Takayama et al., 1997) conducted a study on seismic isolation design through a design method to prepare earthquakes in advance [3-4]. The reaction of the bridges during an earthquake can also be decreased by applying an earthquake isolation bearing. To design an earthquake isolation system, it is necessary to investigate the seismic characteristics and performance of the earthquake isolation devices to be used. A high-damping rubber bearing (HDRB) is one type of earthquake isolation device that is widely used in various countries. HDRBs use a specially mixed rubber to dissipate much energy through deformation. An HDRB has the same configuration as an elastic bearing and has high energy dissipation capability. Recently, studies of HDRB have been carried out actively because it is convenient to manufacture and use in construction. (Hwang et al, 2002) have developed an analytical model to describe the damping and restoring forces of HDRBs. Both stiffness and damping coefficients are expressed in terms of a higher order polynomial function of the relative displacement and velocity of the bearing [5]. (Dall’Asta and Ragni, 2006) conducted cyclic shear tests and simple relaxation tests to identify the rate-dependent mechanical properties of HDRBs and they have proposed a rate-dependent analytical model of HDRBs [6]. (Bhuiyan et al., 2009) developed extended rheology model of HDRBs by adding a nonlinear elastic spring and an elasto-plastic model in parallel and conducted of three types of tests, namely a cyclic shear (CS) test, a multi-step relaxation (MSR) test, and a simple relaxation (SR) test to identify constitutive relations of each element in the rheology model [7].
However, the performance of an HDRB is dependent on the displacement, temperature, frequency, vertical pressure, and load history (Japan Society of Seismic Isolation, 2002). Furthermore, the development of high-damping rubber technology in Korea is in an early phase and thus has not been widely used.
ISO 22762 (2005) [8-9] specifies the minimum required properties of rubber for an HDRB and indicates a shear modulus of 0.4-0.8 MPa for buildings and 0.8-1.2 MPa for bridges. The reason for the requirement of lower hardness for buildings is to ensure stability by decreasing the height of the bearing, and buildings require a longer period than bridges. However, the shear property of a low-hardness bearing should be verified for application to long-period structures with low-hardness bearings to ensure safety. Nonetheless, there has been little in-depth experimental research on the dependence of the shear properties. However, Jeong et al. (2002) and Choi et al. (2008) performed experiments to examine changes in the properties of earthquake isolation bearings according to changes in the environment. More recently, Saiful Islam et al. (2011) examined the effect of incorporation of isolator on the seismic behavior of soft story buildings and carried out dynamic analysis to increase damping ratio of high damping rubber bearings [10]. Sachi et al. (2013) conducted a series of full-scale shaking table tests to investigate the effects of vertical response on building contents and nonstructural components [11].
Furthermore, few studies have examined the possibility of changes in the shear properties according to dependencies of earthquake isolation devices. Masashi et al. (2012) proposed rate-independent model and conducted full-scale tests under horizontal bidirectional loading to examine nonlinear behavior of high-damping rubber bearings [12]. Athanasios et al. (2016) proposed mechanical shear response of high-damping rubber bearing model consisting of nonlinear spring, elastoplastic elements, and hysteretic damper, then simulated the shear behavior under a wide range of strain amplitudes [13].
The present study conducted dynamic property tests using high-damping rubber and manufactured HDRB specimens using rubber with shear moduli of 0.4 MPa and 0.8 MPa. They examined the compressive and shear properties to investigate the seismic performance. This experiment was designed based on previous studies by (Nishio et al., 1997) and (Iwabe N et al., 2000) [14-15]. Dynamic tests were also conducted to determine the effect of environmental changes in accordance with ISO 22762
2. Dynamic properties of high-damping rubber
High-damping rubber features elasticity and returns to its original shape after deformation. Furthermore, its viscosity characteristics absorb deformation energy, so it can be used without an additional damper when applied as a rubber bearing. Property tests were conducted on the rubber material used in the HDRBs, and the characteristics of dependence were investigated.
2.1. Test method
The dynamic tests on the rubber were conducted using the equipment shown in Fig. 1. The tests were done using an EPLEXOR 150N with standard specimens suggested by ISO 22762. Two types of rubber materials with shear moduli of 0.4 MPa and 0.8 MPa were used in the tests. A total of 240 rubber specimens were used (10 specimens for each test condition). The test results are summarized as the mean values for each condition. The dependencies on the displacement, frequency, and temperature were investigated.
The displacement dependence test was conducted by increasing the displacement by 5 % up to 45 % while fixing the frequency and temperature conditions. The frequency dependence test was conducted by increasing the frequency to 0.05, 0.2, and 1.0 Hz while fixing the displacement and temperature conditions. Finally, the temperature dependence test was conducted in a range of temperatures (–20 °C, 0 °C, 20 °C, and 40 °C) to simulate the extreme temperature changes during different seasons. These tests were used to determine the dependencies of the shear modulus and damping ratio.
Fig. 1Dynamic property tester and rubber specimen anchorage

a)

b)
2.2. Dynamic property results
The shear modulus increased as the temperature decreased and the frequency increased. The shear modulus also decreased as the dynamic strain increased. There was a small reduction in the damping ratio with changes in temperature, but the ratio decreased as the temperature increased. Moreover, the shear modulus increased with the frequency and decreased as the dynamic strain increased. Fig. 2 to 5 show the correlation of the shear modulus and the damping ratio with the temperature, frequency, and displacement conditions for different values of the shear modulus of elasticity. As the dynamic displacement decreased, the damping ratio increased, and as the displacement increased, the damping ratio converged to a certain value. As the shear modulus of elasticity increased, the shear modulus also increased while the damping ratio decreased.
Fig. 2Change in shear modulus by temperature, frequency, and displacement (G 0.8 MPa)
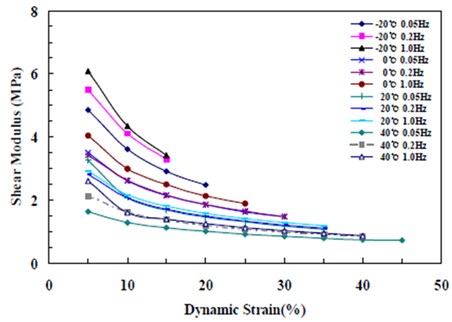
The temperature dependence test results showed that the damping ratio of high-damping rubber increased from 14.5 % to 21.8 % as the temperature changed (–20-40 °C) due to the physical properties of rubber. The rubber material is sensitive to changes in temperature, and the damping ratio was higher at low temperature. The reason for this behavior is the phase difference between the shear modulus of elasticity () and loss modulus () as the molecular binding force between rubber molecules decreases at high temperature. The test results with increasing frequency to 0.05, 0.2, and 1.0 Hz indicated that there was also a dependence on the frequency.
Fig. 3Change in damping ratio by temperature, frequency, and displacement (G 0.8 MPa)
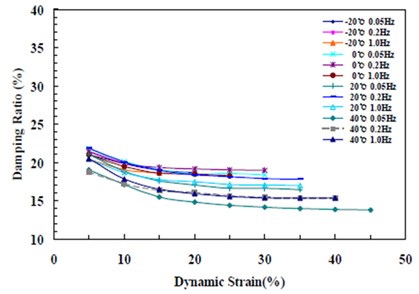
Fig. 4Change in shear modulus by temperature, frequency, and displacement (G 0.4 MPa)
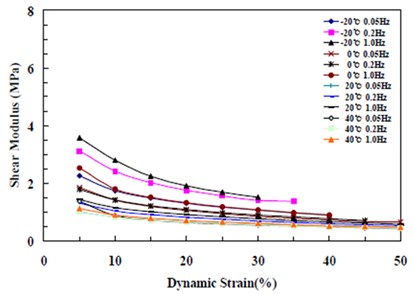
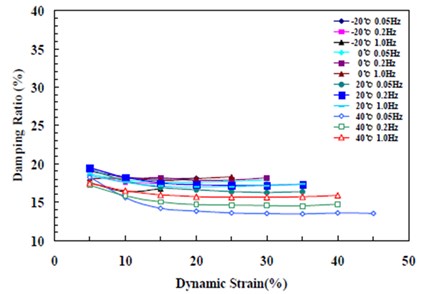
Fig. 5Change in damping ratio by temperature, frequency, and displacement (G 0.4 MPa)
3. Earthquake isolation bearing
3.1. HDRB characteristics
The HDRB used in the shear property test was designed and manufactured based on the dynamic properties of bridges and buildings. The HDRB is composed of laminated rubber and reinforced steel plate. The shape of the HDRB is the same as that of general rubber bearings. However, the HDRB does not need lead since its damping capability is improved through rubber compounding, in contrast to a lead rubber bearing (LRB). Increasing the viscosity of the rubber and the friction can be considered to increase the energy absorption capacity. However, if the viscosity is increased, the fluidity of the material is also increased. As a result, the creep and physical properties tend to degrade rapidly.
The HDRB can absorb energy while deforming and has damping capabilities. The hysteretic behaviors can be changed by changing the rubber compounding, but the energy dissipation capacity is only 15-20 %, in contrast to the 30 % value for an LRB. As a result, the damping capability is somewhat degraded. However, the HDRB has much better damping force than a natural rubber bearing with a similar material and shape (which has an energy dissipation capacity of only 8 %).
The laminated rubber bearing has complex hysteretic behavior that depends on the shear strain. The HDRB has a very large horizontal stiffness at small strain and displacement (<20 %), resulting in strong resistance to the vibration of structures or wind (wind load control stiffness). On the other hand, the HDRB shows a constant horizontal stiffness in the mid-range (20 << 120 %) of strain and displacement, where the change in the restoring force is linear (seismic load control stiffness). At very large shear strain range (<120 %), it shows stiffness properties (ultimate load control stiffness) that suppress extreme shear deformation due to the occurrence of hardening (Koo et al., 1998).
3.2. Specimen design
The HDRB was designed to satisfy the serviceable limit state determined by the design compressive force of bridge structures, the ultimate limit state due to an earthquake, and resistance against wind load. Specimens were fabricated in accordance with ISO 22762, and property tests were conducted. The ISO 22762 standard specifies test methods, design standards, and product inspection standards for laminated rubber bearings for earthquake isolation devices that protect building structures or bridges from earthquakes. Two types of specimens were fabricated according to these design conditions and test evaluation standards with different shear moduli of elasticity ().
3.3. Specimen specifications
Natural rubber has excellent elasticity and restoration ability, and it has been widely used in earthquake isolation bearings. However, the specimens were manufactured using high-damping rubber, which maintains its elasticity and restoration ability and features higher energy absorption capacity in addition to the inherent properties of natural rubber. The specimens had the same size. The outer rubber thickness was 10 mm, and the thickness of one layer inside the laminated rubber was 2 mm. The laminated rubber had 25 layers. The thickness of the reinforced steel plate was 3 mm.
S1 is the primary shape factor, which is the ratio of the load area to the free surface area, including the holes of one rubber layer. S2 is the secondary shape factor, which is the ratio of the effective width to the total thickness of the inner rubber. Table 1 provides more detailed specifications of the specimens, while Fig. 6 and 7 show their shape. Table 2 presents the main composition of the rubber. Generally, the processability of rubber degrades and the strain hardening increases with a higher proportion of carbon black. The HDRBs were made from high-damping rubber with shear moduli of elasticity of 0.4 MPa and 0.8 MPa at 100 % shear strain. The HRDBs were manufactured with a circular shape in accordance with the specifications for a standard test piece recommended in ISO 22762.
3.4. Tester specifications
The specifications and a photo of the property tester are presented in Table 3 and Fig. 8. The tester is a compression-shear tester with a maximum vertical load of 2.000 kN and maximum horizontal load of 500 kN. The maximum horizontal speed is 300 mm/sec, and the maximum horizontal displacement is ±200 mm.
4. Property test results and analysis
Compression and shear property tests were carried out to investigate the compressive stiffness, shear stiffness, and damping ratio. The results were compared with corresponding design values calculated via the design equation from ISO 22762 to verify whether the errors were within acceptable ranges. The range of error for the compressive stiffness is ±30 %, and that for the shear property is ±10 %, which are the standards for the S-A grade. The results showed that the high-damping rubber properties were dependent on the shear deformation, frequency, and temperature.
4.1. Compression and shear property tests
4.1.1. Compression property tests
Two displacement gauges were installed on the specimens at room temperature to measure the vertical stiffness. The vertical stiffness was measured by applying three loads from –30 % to +30 % based on the design load P0 (vertical pressure of 7.5 MPa), as shown in Fig. 9. The vertical stiffness was then calculated using Eq. (1). X1 and X2 are the displacements at loads P1 and P2 in the third cycle, respectively.
Table 1Specifications of the laminated rubber bearing specimen
Item Specimen | Steel plate diameter (mm) | Hole diameter (mm) | Total diameter (mm) | Rubber thickness (mm) | No. of rubber layers (n) | Steel plate thickness (mm) | Axial stress (MPa) | Shear modulus of elasticity () | ||
HDRB 1 | 240 | 12.5 | 250 | 2 | 25 | 3 | 29.7 | 5 | 7.5 | 0.8 |
HDRB 2 | 240 | 12.5 | 250 | 2 | 25 | 3 | 29.7 | 5 | 7.5 | 0.4 |
S1 is the primary shape factor , and S2 is the secondary shape factor. is the diameter of the inner reinforced steel plate, is the diameter of the inner hole, is the thickness of one rubber layer, and n is the number of rubber layers:
The compression test results showed that the maximum and minimum loads at the third cycle were 481 kN and 259 kN for HDRB 1 (0.8 MPa) and the displacements were 0.80 mm and 0.56 mm, respectively. For HDRB 2 (0.4 MPa), the maximum and minimum loads at the third cycle were 455.08 kN and 264.65 kN, and the displacements were 0.79 mm and 0.58 mm, respectively. These values were applied to Eq. (1) to calculate the compressive stiffness, and the results were 1,393 kN/mm and 907 kN/mm, respectively. To verify whether the measured values satisfied the standard requirements, the compressive elastic modulus was calculated using Eq. (2), and the design value of the compressive stiffness was calculated using Eq. (3):
where is the shape factor, is the total thickness of rubber, and is the vertical stiffness. The elastic moduli used for the HDR, which is an anisotropic material, were 2.4 MPa and 1.2 MPa, respectively, which are three times the shear modulus. A correction factor of 0.865 was used due to the rubber's hardness (Mineo Takayama, 1997), and a bulk modulus of elasticity of 2.000 MPa was used based on AASHTO (1999). The resulting experimental values of the compressive stiffness had errors of –10 % and –3 % compared to the design values, respectively. The correction factor and bulk modulus of elasticity were also determined to be reasonable. Table 4 summarizes the experimental and design values of the compressive stiffness.
Table 2Basic compositions of the high-damping rubber (weight ratio, %)
Item Specimen | Natural rubber | Carbon black | Vulcanizing agent | Additive |
HDRB 1 | 59.1 | 26.1 | 0.7 | 14.1 |
HDRB 2 | 52.6 | 34.0 | 0.8 | 12.6 |
Fig. 6Specifications of a specimen
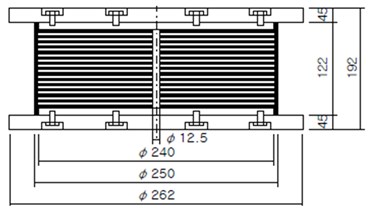
Fig. 7HDRB specimens

Fig. 82.000 kN compression-shear tester

Fig. 9Loading curve of compressive load
Table 3Specifications of 2.000 kN compression-shear tester
Max load | Max displacement | Max speed | |
Vertical capacity | ±2000 kN | ±100 mm | 100 mm/sec |
Horizontal capacity | ±500 kN | ±200 mm | 250 mm/sec |
Table 4Test results of compression property
Category | Design value | Experimental value | Standard range | Error |
HDRB 1 | 1.538 | 1.393 | ±30 % | –10 % |
HDRB 2 | 936 | 907 | ±30 % | –3 % |
4.1.2. Shear property tests
The shear property tests were conducted as shown in Fig. 10 to obtain the equivalent shear stiffness (Kh) and equivalent damping ratio (heq) of the HDRB. The tests were conducted to generate a lateral displacement of 50 mm in the total rubber thickness as the calculated design shear displacement using 0.5-Hz sine waves for the vertical load to maintain a vertical design pressure of 7.5 MPa at the room temperature. The loads were repeatedly applied to the specimens 11 times, and the mean of the history curves from the second to the eleventh load was calculated.
The equivalent shear stiffness at the th cycle was calculated using Eq. (4):
where and are the maximum and minimum shear forces at the th cycle, while and are the maximum and minimum displacements at the th cycle (Fig. 11). The equivalent damping ratio at the th cycle was calculated using Eq. (5):
where is the area surrounded by the history curve in the th cycle. The mean value of the second to the eleventh cycles was used to calculate the shear stiffness and equivalent damping ratio of the HDRB:
The results are presented in Table 5. The equivalent shear stiffness of HDRB 1 was 0.814 kN/mm, and the equivalent damping ratio was 15.9 %. The results for HDRB 2 were 0.414 kN/mm and 19.5 %, respectively. The design values of the equivalent shear stiffness were calculated as 0.783 and 0.392 kN/mm, respectively, but the design equation of the equivalent damping ratio was not given in the standard. Thus, only the equivalent shear stiffness was compared with the corresponding design values:
Table 5 presents the resulting experimental and design values of the equivalent shear stiffness. Compared to the design values, the test results of the equivalent shear stiffness had errors of 3.9 % and 5.7 %, respectively. Thus, both of the errors were within the standard reference range of ±15 %.
Fig. 10Compression-shear loading curve
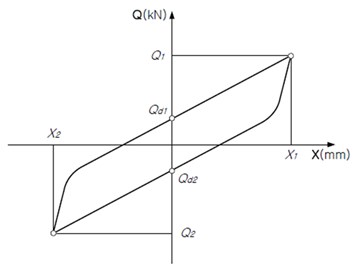
Fig. 11Shear property test

Table 5Shear property results
Category | Design value | Experimental value | Standard range | Error | Equivalent damping ratio |
HDRB 1 | 0.783 | 0.814 | ±15 % | 3.9 % | 15.9 % |
HDRB 2 | 0.392 | 0.414 | ±15 % | 5.7 % | 19.5 % |
4.2. Shear property dependence test
4.2.1. Shear strain dependence test
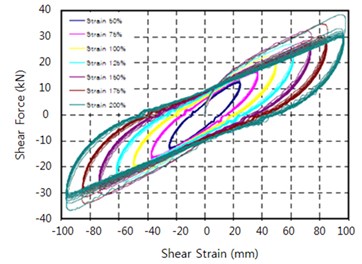
The compression-shear tests were conducted with various shear displacements to investigate the changes in equivalent shear stiffness and equivalent damping ratio according to shear strain of the HDRB. The required shear displacements were repeatedly applied as 0.5-Hz sine waves 11 times while constant vertical loading was applied to maintain the vertical design pressure at room temperature. The shear strains in the tests were 50 %, 75 %, 100 %, 125 %, 150 %, 175 %, and 200 %, and the number of cycles was the same as in the shear test.
Fig. 13 shows the history curves indicating the dependence on the shear strain in the tests. The rates of change of the equivalent shear stiffness and equivalent damping ratio were calculated based on the test values at 100 % shear strain, which are shown in Fig. 12. Both the equivalent shear stiffness () and equivalent damping ratio () in the range of 50-200 % shear strain showed decreasing trends as the shear strain increased. However, a change of approximately 45 % occurred in the equivalent shear stiffness, which exhibited a large dependence on the shear strain. However, the equivalent damping ratio decreased by up to 5 %, indicating a small dependence on the shear strain. Thus, Eq. (9) was used during bearing design, which considers the dependence on the shear strain, in contrast to Eq. (8):
Eq. (10) is an empirical equation of the shear modulus of elasticity that considers the dependence on the shear strain. The equation is based on the test results and was calculated through regression analysis, and the results are shown in Fig. 12:
Fig. 12Changes in equivalent shear stiffness and damping ratio according to shear strain
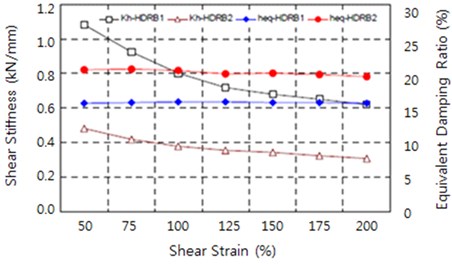
Fig. 13Shear strain dependence test results
4.2.2. Compressive stress dependence test
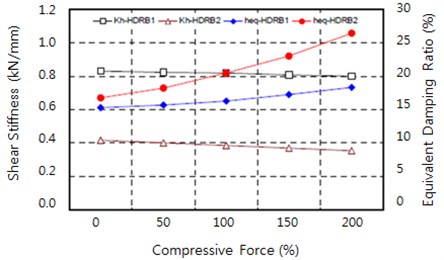
Compression-shear tests were conducted with various compressive stresses to determine the dependence of the equivalent shear stiffness and equivalent damping ratio. A constant vertical load was applied to maintain the vertical design pressure at room temperature condition. The design shear displacement ( 100 %) was repeatedly applied as 0.5-Hz sine waves 11 times. The tests were conducted with five vertical pressures corresponding to 0 %, 50 %, 100 %, 150 %, and 200 % of the vertical design pressure of 7.5 MPa.
Fig. 14 shows the resulting rates of change of the equivalent shear stiffness and equivalent damping ratio. The equivalent shear stiffness tended to decrease as the vertical pressure increased. It changed by 4 % in HDRB 1 and 17 % in HDRB 2, which exhibited a relatively small dependence on the vertical pressure. The equivalent damping ratio tended to increase as the vertical pressure increased, in contrast with the results of the equivalent shear stiffness. The rate of change in the damping ratio of HDRB 2 was –19 to 28 %, showing a high dependence on the vertical pressure. The reason for the high dependence of the equivalent damping ratio on the vertical pressure is the increase in viscosity and friction-induced factors between rubber molecules as the vertical pressure increased. Thus, it is necessary to consider the vertical design pressure when determining the design value of the equivalent damping ratio.
Fig. 14Changes in equivalent shear stiffness and equivalent damping ratio according to vertical pressure
4.2.3. Frequency dependence test
The compression-shear tests were conducted with various frequencies to determine the changes in the equivalent shear stiffness and equivalent damping ratio according to frequency. A constant vertical load was applied to maintain the vertical design pressure of 7.5 MPa at room temperature, and the design shear displacement was applied 11 times as a 0.5 Hz sine waves. The frequencies used in the tests were 0.005, 0.01, 0.1, 0.25, 0.5, and 0.7 Hz. Frequencies above 0.7 Hz were not investigated due to the speed limitations of the test equipment.
The test results are shown in Fig. 15, for which the rates of change in the equivalent shear stiffness and equivalent damping ratio were calculated based on the value at 0.5 Hz. Both the equivalent shear stiffness and equivalent damping ratio showed an increasing tendency as the frequency increased in the range of 0.001-0.5 Hz.
Fig. 15Changes in shear stiffness and equivalent damping ratio according to changes in frequency
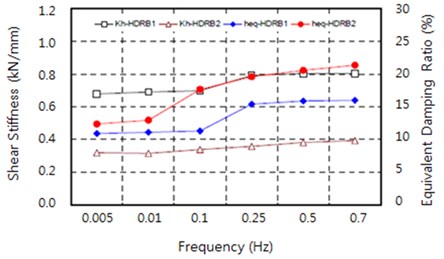
However, the tendency was significantly different before and after 0.25 Hz. Both the equivalent shear stiffness and equivalent damping ratio showed stable rates of change below 11 % at frequencies above 0.25 Hz. In contrast, they both decreased rapidly at frequencies below 0.25 Hz. For HDRB 1, rates of change of the equivalent shear stiffness and equivalent damping ratio were –2 to –16 % and –32 to –4 %, while for HDRB 2, they were –17 to 3 % and –40 to 3 %, respectively. The reason for the larger change in the equivalent damping ratio according to frequency was that the compounding agents applied to the high-damping rubber contributed significantly to the viscosity and friction-induced factor between rubber molecules.
4.2.4. Temperature dependence test
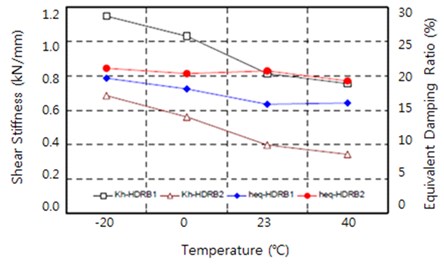
The temperature-dependence results are shown in Fig. 16. The test methods were the same as that of the shear property test except that the temperatures were set to –20 °C, 0 °C, 23 °C, and 40 °C. A thermostatic chamber was installed around the tester. The specimens were stored in a thermos-hygrostat for three days at these temperatures and then mounted in the tester. Liquid nitrogen was used to maintain a low temperature for low-temperature tests, and a heating fan was used to maintain the high temperatures.
Fig. 16Photo of then temperature dependence test

The test results are shown in Fig. 17. The rates of change in the equivalent shear stiffness and equivalent damping ratio were calculated based on the value at 23 °C. The equivalent shear stiffness showed a decreasing trend in the temperature range of –20-40 °C as the temperature increased. However, the change in equivalent damping ratio decreased somewhat but maintained an almost constant rate. The rate of change in the equivalent shear stiffness was up to 41 % for HDRB 1 and up to 72 % for HDRB 2. The elasticity of polymer materials such as rubber changes according to temperature. In particular, it increases rapidly at the glass transition temperature and at low temperature. For high-damping rubber, various compounding agents are added to improve the damping performance, such as plasticizers, softeners, and reinforcing agents. These agents create a dependence on temperature, and the properties can vary significantly depending on the types of agents and amounts used.
In general, the HDRB has a relatively high dependence on temperature compared to a natural rubber bearing. The equivalent shear stiffness and damping are high at low temperature and low at high temperature. These properties can be verified by the test results of the temperature dependence from manufacturers, such as Toyo Rubber Industry Co., Ltd. in Japan. The manufacturer data indicates that at a reference temperature of 20 °C, the equivalent shear stiffness increases by 23-40 % and the damping ratio increases by 10-26 % at –10 °C. At 40 °C, the equivalent shear stiffness decreases by 7-13 % and the damping ratio increases by 3-12 %. These results are similar to our test results. In South Korea, the Standard Specifications for Highway Bridges (2005) indicate that the change in the shear modulus of elasticity at low temperature should be three times lower than that at room temperature for finished products of elastic bearings in the performance regulation with regard to rate of change of the shear property.
Fig. 17Changes in equivalent shear stiffness and equivalent damping ratio according to temperature
4.2.5. Cyclic load dependence test
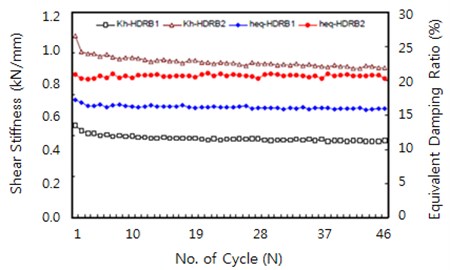
The changes in equivalent shear stiffness and equivalent damping ratio according to cyclic loading were next examined. The design shear displacements were applied 11 times as 0.5 Hz sine waves with constant vertical loading at the vertical design pressure at room temperature. To distinguish the effects of cyclic loading from those of the temperature rise, the shear displacement was repeatedly applied 50 times to the specimen, which was cooled to the initial pre-load temperature prior to applying the load, and then the shear properties were measured again.
Fig. 18 shows the trends with respect to the 50 cycles. The equivalent shear stiffness changed significantly in the first to third cycles and then gradually decreased as the rate of change was decreased. Yasuki Otori (1994) performed 10 excitations while assuming that an earthquake has an oscillation frequency of 0.5 Hz with ±200 % shear strain. The temperature rise in the specimen was approximately 5 °C, and the horizontal stiffness and damping changed by approximately –5 %. The effect of the dependence on the cyclic load was concluded to be minimal. He also reported degraded results where the temperature rise in the specimen was approximately 70 °C, the horizontal stiffness was approximately 20-25 %, and the damping was approximately –25 % when 200 excitations were applied.
After 50 loading cycles, the specimens were placed at room temperature for 24 hours to recover the initial temperature prior to applying the cyclic load, and then the compression-shear tests were conducted again using the same conditions. The test results showed that the equivalent shear stiffness increased by approximately 4.57 % in HDRB 1 and 0.75 % in HDRB 2. The equivalent damping ratio decreased by 1.83 % for HDRB 1, but there was no change in HDRB 2. Since the decrease in the shear property was minimal, permanent deformation due to the cyclic load is highly unlikely.
Fig. 18Changes in shear property according to the number of load cycles
5. Conclusion
The dependence of the shear properties was investigated using HDRB specimens made of rubber materials with different shear moduli of elasticity. The analysis and comparison results are summarized as follows:
1) The shear modulus of elasticity and damping ratio of the HDRB decreased as the displacement, temperature, and frequency increased.
2) The equivalent damping ratio showed a significant dependence on the frequency and vertical pressure but only a small dependence on the temperature and shear strain. The strong dependence of the equivalent damping ratio on the vertical pressure indicates a strong dependence of the strength properties. Thus, it is necessary to consider the vertical pressure during the design of the equivalent damping ratio for the HDRB.
3) The equivalent shear stiffness exhibited a strong dependence on the temperature and shear strain but only a small dependence on the vertical pressure. Thus, it is necessary to consider the temperature and shear strain to estimate the equivalent shear stiffness of the HDRB. Furthermore, the equivalent shear stiffness decreased as the temperature increased, and a significant change occurred at low temperature.
4) There was little change in the equivalent shear stiffness after 50 load cycles. This occurred because hysteresis damping was rarely present in the inner rubber used in the specimen, and the factor of change in the physical properties such as the inner temperature rise was small. In addition, as the frequency increased, the effective stiffness increased at a small rate in the frequency dependence test.
5) The results indicate that calculating the shear stiffness and equivalent damping ratio requires in-depth analysis that considers the dependence of the properties on the design displacement, vertical pressure, temperature, and excitation velocity, which are the main design variables for HDRBs.
6) The present study was conducted with only standard test pieces recommended by ISO 22762-1. Thus, it is necessary to conduct additional tests with different shape factors to determine the effects of the specimen size.
References
-
Aiken I. D., Kelly J. M., Clark P. W. Experimental studies of the mechanical characteristics of three types of seismic isolation bearings. Proceeding 10th World Conference on Earthquake Engineering, 1992.
-
Takayama M. Ultimate capacity of natural rubber bearings used in seismic isolation system. Journal of the Architectural Institute of Japan, Vol. 1, 1995, p. 160-165.
-
Robinson W. H. Lead rubber hysteretic bearing suitable for predicting structures during earthquakes. International Journal of Earthquake Engineering and Structural Dynamics, Vol. 10, Issue 4, 1982, p. 5-19.
-
Mineoh Takayama Road to 4 Seconds Seismic Isolation – Seismic Isolation Structure Design Manual. The Science and Engineering Books, 1997.
-
Hwang J. S., Wu J. D., Pan Yang C. T. G. A mathematical hysteretic model for elastomeric isolation bearings. Earthquake Engineering and Structural Dynamics, Vol. 31, 2002, p. 771-789.
-
Dall’asta A., Ragni L. Experimental tests and analytical model of high damping rubber dissipating devices. Engineering Structures, Vol. 28, 2006, p. 1874-1884.
-
Bhuiyan A. R., Okui Y., Mitamura H., Imai T. A rheology model of high damping rubber bearings for seismic analysis: Identification of nonlinear viscosity. International Journal of Solids and Structures, Vol. 46, 2009, p. 1778-1792.
-
Elastomeric Seismic Protection Isolators Part 1: Test Methods. Iso22762, 2005.
-
Elastomeric Seismic Protection Isolators Part 2: Applications for Bridges. Iso22762, 2005.
-
Saiful Islam A. B. M., Mohammed Jameel, Syed Ishtiaq Ahmad, Mohd Zamin Jumaat Study on corollary of seismic base isolation system on buildings with soft storey. International Journal of the Physical Sciences, Vol. 6, Issue 11, 2011, p. 2654-2661.
-
Sachi F., Eiji S., Yundong S., Tracy B., Masayoshi N. Full-scale shaking table test of a base-isolated medical facility subjected to vertical motions. Journal of the International Association for Earthquake Engineering, Vol. 42, Issue 13, 2013, p. 1931-1949.
-
Masashi Y., Shigeo M., Harumi Y., Masahiko H. Nonlinear behavior of high-damping rubber bearings under horizontal bidirectional loading: full-scale tests and analytical modeling. Journal of the International Association for Earthquake Engineering, Vol. 41, Issues 13-25, 2012, p. 1845-1860.
-
Athanasios A. M., George D. M. Mechanical models for shear behavior in high damping rubber bearings. Soil Dynamics and Earthquake Engineering, Vol. 90, 2016, p. 221-226.
-
Nishio K., Ishihara T., Yanagisawa N., Matsubayashi Y., Fujinami T. Study on tensile performance of base isolation devices. Part 2-tensile loading test of full sized high damping laminated rubber bearing. Summaries of Technical Papers of Annual Meeting, 1997, p. 529-530.
-
Iwabe N., Takayama M., Kani N., Wada A. Experimental study on the effects of tension for rubber bearings. 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 2000.
Cited by
About this article
This research was supported by Yeungnam University Research Grant in 2017.
