Thickness shear vibration of a ZnO film structure covered with magnetic fluid

1. Introduction

The last couple of decades has seen the successful deposition of an ultra-thin piezoelectric film of Aluminium-Nitride (AlN) or Zinc oxide (ZnO) on a silicon layer, laying the basis for thin-film bulk acoustic resonator (FBAR) working in the GHz frequency range [1-3]. The c-axis of the FBAR orients itself along the normal/in-plane direction of the film, deviates from the direction by a certain angle, or zigzags in a multilayer film [4-8]. It is possible to excite a pure shear vibration mode at a specific c-axis angle. The shear vibration can be detected with high sensitivity in the liquid environment, for the vibration is not damped due to the lack of compression. Hence, thickness shear mode sensors have been developed to detect compounds coated with surface bound receptive layers in gases or liquids. In particular, the FBAR has been utilized to make acoustic wave sensors for mass and fluid sensing [9-12].

For sensor applications, the resonator is usually capped with a thin chemical/physical sensitive film, e.g. the thin multilayer piezoelectric film. Over the years, much research has been done on magnetoelectric structures containing magnetic and ferroelectric/piezoelectric layers [13], because of their interesting properties for data storage [14]. As a magnetoelectric structure, the magnetic fluid hosts widely dispersed magnetic particles. In a certain sense, the fluid is “smart” because its viscoelasticity can be controlled by the intensity of the magnetic field. Thanks to the unique feature, the fluid has been increasingly applied in the sensor field. For instance, the magnetic fluid has been successfully implemented in vehicle acceleration sensor [15], angle sensor [16] and volumetric sensor [17]. Nevertheless, reports on the application of multilayer magnetic fluid structures few and scattered at present [18].

To make up for the gap, this paper proposes a thin film sensor coated with magnetic fluid layer (Figure 1). In general, a resonator consists of a thin layer of piezoelectric material and two electrodes on both sides. When an AC electric field is applied across the electrodes, acoustic waves come into being and start to propagate across the device. The propagation amplitude and phase depend on the interfacial reactions and the thin film parameters, including thickness, density, and complex shear modulus. Under the action of magnetic field, the magnetorheological properties change, and act on the piezoelectric thin film by sound wave. The variation in amplitude and phase, in turn, changes the electrical properties of the resonator. Based on piezoelectric elastic theory, viscoelastic mechanics and liquid mechanics, specifically, the author analysed the thickness shear vibration of ZnO thin film covered with a finite-thickness layer of magnetic liquid. The author investigated the propagation properties of bulk acoustic waves in the multilayer piezoelectric thin film with a tilted c-axis, seeking to derive the analytical method for bulk acoustic waves and aiming to disclose the effect of magnetic liquid on the shift of resonant frequency.

2. Governing equation

As shown in Fig. 1, the research object is the thickness shear vibration of a tilted c-axis ZnO film structure covered with magnetic fluid. The top and bottom surfaces of the film are positive and negative electrodes, respectively. The two layers were treated separately before applying the continuity and boundary conditions. The edge effect was neglected in view of the large length/thickness and width/thickness ratios. Then, a basic 1D theoretical model was constructed depending on the plate thickness and time. The 1D model depicts the basic behaviours of FBARs, and predicts the pure thickness resonant frequencies and modes. The model has nothing to do with the in-plane coordinates of the film, and varies only along the film thickness with one spatial variable along the normal direction of the layers. The model was constructed in the following steps.

Fig. 1A ZnO film structure with inclined c-axe covered with magnetic liquids. 2h is the thickness of the ZnO film. θ is the c-axis tilt angle of the ZnO film

Consider the following displacement fields that describe the thickness shear motion of interest, the displacement and electric potential fields are assumed to take the following forms [19]:

The differential equations of thickness shear motion and ZnO electrostatics [20] with a compact matrix notion[21] can be written as:

where $T_5$, $u_1$ and $D_3$ are thickness shear stress $T_{13}$, horizontal displacement, and vertical electric displacement, respectively; $\rho$ is the mass density of ZnO. In the following analysis, the mass and stiffness of the electrodes are neglected, the subscript comma denotes a partial derivative with respect to the coordinates, and a superimposed dot represents the derivative with respect to the time. Then, the strain-displacement and electric field-potential relations [20, 21] are:

The nontrivial components of the stress and electric displacement [20, 21] are expressed as:

Considering time-harmonic motions, the commonly used complex notation is adopted for this research. All the fields sharing the same time dependence with a common factor $\mathrm{e}\mathrm{x}\mathrm{p}\left(i\omega t\right)$ are presented below. Substituting Eqs. (4a)and (5) into Eq. (2), and substituting Eqs. (4b) and (6) into Eq. (3), we have:

where ${\stackrel{-}{c}}_{55}=c_{55}+e_{35}^2/{\epsilon }_{33}.$

The general solution to Eqs. (7), (8) can be written as:

where $\xi =\omega \sqrt{\rho /{\stackrel{-}{c}}_{55}}$ is the wave number for the thickness shear mode; $A$, $B$, $C$ and $D$ are the unknown amplitudes determined by the boundary conditions.

As mentioned above, the magnetic fluid hosts widely dispersed magnetic particles, and its viscoelasticity can be controlled by the intensity of the magnetic field. The pressure gradient is negligible because only the shear deformation occurs. Hence, the governing equations for the liquid are simplified as:

where ${\mu }^L$, ${\nu }^L$, ${\rho }^L$ and $T^L$ are the dynamic viscosity coefficient, velocity, density and stress of the magnetic liquid, respectively.

The magnetic field was considered to be uniform, and the external magnetic field vector was regarded as perpendicular to the vorticity. Then, the dynamic viscosity coefficient can be expressed as [18]:

where ${\eta }_0$ is the magnetic fluid viscosity coefficient without external magnetic field; $\varphi$ is the fraction of solid; $\varphi$ and $L\left(\psi \right)$ is the Langevin function. In addition, ${\eta }_0={\eta }_c{[1-\frac{5}{2}\tilde{\varphi }+1.55{\tilde{\varphi }}^2]}^{-1}$ [22], where $\tilde{\varphi }$ is the volume fraction of the suspended material and ${\eta }_c$ is the kinetic viscosity coefficient of the current carrier. The parameter $\psi$ is calculated by $\psi ={\mu }_{0}mH/k_{0}T$, where $T$ is the ambient temperature, $m$ is the magnetic moment of single solid particle, $k_0$is the Boltzmann constant, ${\mu }_0$ is the vacuum permeability, and $H$ is the external magnetic field. Based on the value of $\psi$, it is easy to obtain the numerical value of Langevin function $L\left(\psi \right)=\mathrm{c}\mathrm{o}\mathrm{s}\psi -1/\psi$.

The general solutions to Eqs. (10), (11) can be written as:

where:

Since $x_3\to +\propto$, ${\nu }^L$ is finite, the second term of Eq. (14) must be removed if $B^L=$0.

3. Boundary conditions and solutions

The continuity conditions at the interface between the thin film and the magnetic fluid are:

The stress boundary conditions at the bottom of the film is:

When the driving electrode is shorted to the ground electrode, the electric potential boundary conditions are:

Substituting Eqs. (9), (10) and (14), (15) into Eqs. (17)-(20), it is possible to derive the algebraic equations of the integration constants:

To find the nontrivial solutions to the integration constants, the coefficient matrix of these linear algebraic equations must be equal to zero. This yields the frequency equation below, which determines the resonant frequencies of the plate carrying the magnetic fluid:

For forced vibration, the boundary conditions are:

The current of the FBAR is expressed by $I=dQ/dt=-i\omega {\epsilon }_{33}CS$. The output impendence can be expressed as:

where $S$ is the electrode area; $i$ is the imaginary unit. The numerical solutions of Eqs. (26) and (29) are obtained with Matlab by selecting appropriate parameters.

4. Numerical results and discussion

In our numerical example, the thickness of the ZnO film is $2h=$3 μm and the electrode area is $S=$9×10^-8m². These are the typical values for thin film AlN and ZnO resonators. Whereas $\sqrt{S}/2h=\text{100}$, the length/thickness ratio is sufficiently large to make pure thickness shear vibration with negligible edge effect. The c-axis inclination is $\theta =$ 43° [23], whose $e_{35}$ is large and $e_{33}$ is virtually zero [5]. Hence, thickness shear vibration can be excited easily without stretching the thickness.

The constants in the $\left(x,y,z\right)$ system of ZnO are derived from a widely accepted reference for material data [24]. In the $\left(x,y,z\right)$ system, the material constants are as follows:

The material constants of ZnO with $c$-axis tilted 43° were obtained by tensor transformation. The constants in our calculation are listed in Table 1. Some of the geometric parameters of magnetic fluid fixed for all calculations are presented in Table 2. The other geometric parameters are specified separately in individual figures. Based on Eqs. (26), (29) and material constants, the resonator spectrum with magnetic fluids was simulated.

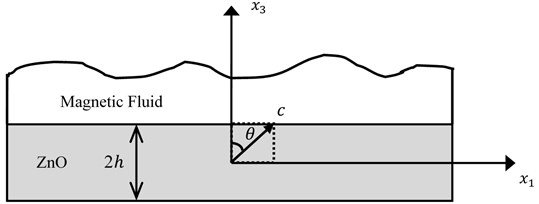
For free vibration, the frequency shift curves are shown in Figs. 2-5. Here into, Fig. 2 (${\rho }^L=$800 kg/m³) and Fig. 3 ($\tilde{\varphi }=$ 0.45) depict the shift of the resonant frequency versus viscosity coefficient, when the external magnetic field is fixed at $H=$ 1×10⁴ A/m. There are three different curves of volume fraction $\tilde{\varphi }$ in Fig. 2 and three different curves of density ${\rho }^L$ in Fig. 3. The relative resonant frequency increases with the viscosity coefficient. In other words, the frequent shift is more prominent at greater values of $\tilde{\varphi }$ and ${\rho }^L$. Moreover, it can be seen that the three volume fraction curves are more separated than the three density curves.

Fig. 4 (${\rho }^L=$ 800 kg/m³) and Fig. 5 ($\tilde{\varphi }=$ 0.45) illustrate the shift of the relative resonant frequency versus uniform magnetic field at the fixed viscosity coefficient of ${\eta }_c=$ 10 N·s/m². The three density curves ($\tilde{\varphi }=$ 0.2; 0.45; 0.6) in Fig. 4 are almost parallel to the $x$-axis, and are virtually unchanged with the increase in the uniform magnetic field. This means the magnetic field has a weak effect on the acoustic waves of the ZnO piezoelectric film. In Fig. 5, the relative resonant frequency increases with the uniform magnetic field, that is, the frequency shift is positively correlated with density. In comparison, the effect of magnetic field is more pronounced in Fig. 5.

Fig. 2Relative resonant frequency versus viscous coefficient with different volume fraction

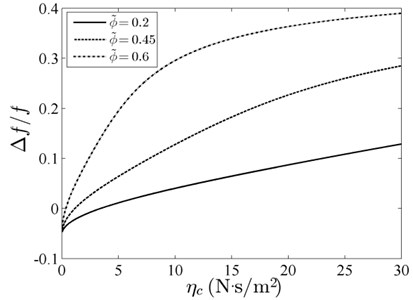
Fig. 3Relative resonant frequency versus viscous coefficient with different density

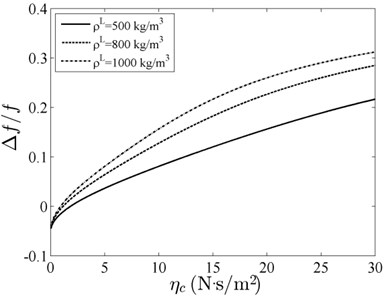
Fig. 4Relative resonant frequency versus uniform magnetic field with different volume fraction

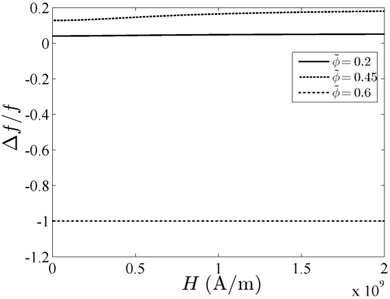
Fig. 5Relative resonant frequency versus uniform magnetic field with different density

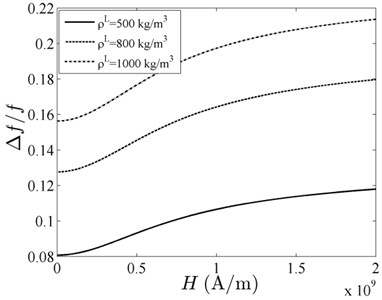
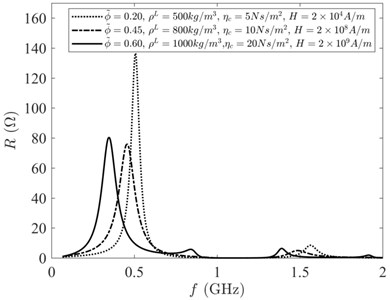
For forced vibration, Fig. 6 shows the output impedance versus the driving frequency at ${\rho }^L=$ 800 kg/m³, ${\eta }_c=$10 N·s/m² and $H=$ 1×10⁴ A/m, and the three values of $\tilde{\varphi }$; Fig. 7 presents the output impedance versus the driving frequency at ${\eta }_c=$ 10 N·s/m², $\tilde{\varphi }=$ 0.45 and $H=$ 1×10⁴ A/m and the three values of ${\rho }^L$; Fig. 8 illustrates the output impedance versus the driving frequency at ${\rho }^L=$ 800 kg/m³, $\tilde{\varphi }=$ 0.45 and $H=$ 1×10⁴ A/m and the three values of ${\eta }_c$.

In Fig. 6, there are three resonant peaks of the curves, and the curve ($\tilde{\varphi }=$ 0.6) differs from the other two. It is special that the curve ($\tilde{\varphi }=$ 0.6) stays at frequency about 0.8 GHz. The larger the volume fraction, the stronger the interface interaction and the more resonant peaks. In the given frequency range, there is a resonant peak much higher than the other peaks, and the output impedance reaches the maximum value in Figs. 6-10. The resonant frequencies of ZnO FBARs decrease, because the resonator is being loaded with magnetic fluid. With the increase of the volume fraction $\tilde{\varphi }$, the density ${\rho }^L$and the ${\eta }_c$, the resonant frequency plunges, but the resonant peaks grow in size. Due to the small damping of the material, the resonance peaks are sharp, and the output impedance is significant near resonance. In Fig. 10, it seems that there are more than three resonant peaks of curve ($\tilde{\varphi }=$ 0.6). As shown inFig. 6 and Fig. 10, the resonant peakschange alike. The volume fraction of magnetic particles apparently has a stronger impact on the acoustic waves of the ZnO piezoelectric film than the other three factors.

Fig. 6Output impedance spectrum with different volume fraction

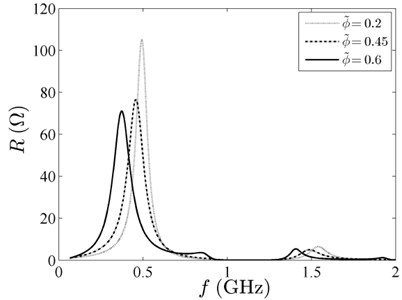
Fig. 7Output impedance spectrum with different density

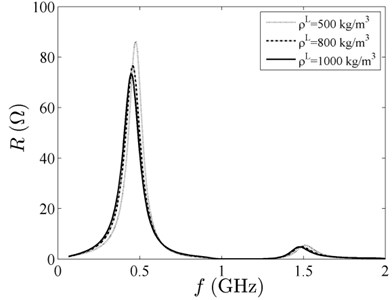
Fig. 8Output impedance spectrum with different viscous coefficient

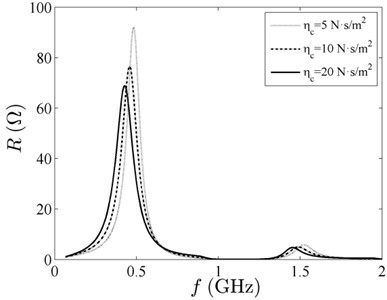
Fig. 9Output impedance spectrum with different magnetic field intensity coupling

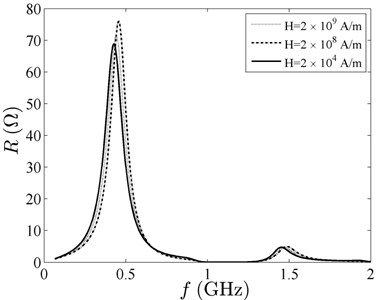
Fig. 10Output impedance spectrum with different coupling of the volume fraction, density, viscous coefficient, magnetic field intensity coupling

5. Conclusions

This paper analyses the thickness shear vibration of ZnO film covered with a finite-thickness layer of magnetic liquid. The analysis reveals that relative resonant frequency and the output impedance are sensitive to various design parameters. Specifically, the relative resonant frequency is positively correlated with the intensity of magnetic field, and the viscosity coefficient, density and volume fraction of magnetic fluid. Under the same viscosity coefficient and density, the magnetic field has a weak effect on the shift of the relative resonant frequency. By contrast, the effect of magnetic field is obvious when the density varies and the other two parameters are constant. For forced vibration, a resonant peak is much higher than other peaks, and the output impedance reaches the maximum in the given frequency range. Moreover, with the increase of the volume fraction $\tilde{\varphi }$, the density ${\rho }^L$ and the kinetic viscosity coefficient ${\eta }_c$, the resonant frequency plunges, but the resonant peaks grow in size.