A roller bearing fault diagnosis method using interval support vector deterministic optimization based on nested PSO

1. Introduction

As a key component of the mechanical system, roller bearing often causes disorder for the race fault, ball fault etc. These faults bring great security risks to the mechanical system. Therefore, the fault diagnosis of roller bearing is of tremendous practical significance in engineer [1-4]. Traditional fault diagnosis methods only aim at deterministic fault samples, ignoring the uncertainty of the samples. However, the uncertainty of the samples should never be ignored. For these years, many scholars have harvested some representative research achievements in uncertainty interval data classification. Based on probability density, Sutar puts forward an interval data classification which extends classical decision tree algorithms to handle data with interval values [5]. Li et al. propose an interval data decision tree classification algorithm which combined with evidence theory [6]. Naive Bayes, as a widely used classification method for deterministic samples, has aroused a lot of interest among relevant researchers. Qin et al. create NBU1 and NBU2 [7]. NBU1 and NBU2 both use the parameter estimation method based on Gauss distribution assumption to calculate the class conditional probability density function of interval data. There is a slight difference between the above two methods in processing of the interval data model. However, NBU1 and NBU2 need the accuracy type of the class conditional probability density function of uncertain data. FBC algorithm, proposed by Ren etc., assumes uncertain interval data to meet the Gauss distribution [8]. The non parametric estimation in the Parzen window method is applied to calculate the types of the class conditional probability density function of interval samples. However, as a lazy learning method, FBC needs all training samples to predict each rolling bearing fault repeatedly. Therefore, both the computational complexity and the memory requirements of this method are too enormous to be offered in fault diagnosis fields.

Support vector machines (SVM) is proposed by Vapnik [9]. Since structured risk minimization is applied in this method, it enables SVM to generalize better in the unseen interval testing samples than neural networks etc. which apply empirical risk minimization [10]. SVM can solve various problems in most of learning methods, such as small samples, nonlinearity, over fitting, high dimension. To make full use of these advantages, an ISVD model is proposed for the fault classification problem of uncertainty roller bearing samples. Meanwhile, the midpoint and the radius are optimized in this deterministic model. These two deterministic objective functions can be converted into a single objective optimization model by the linear combination. ISVD has Lagrange multiplier vector and interval sample vectors. These two groups of vectors are nested. The nested PSO algorithm is constructed based on the dynamic decreasing inertia weight PSO [11]. The advantages of nested PSO include excellent global optimization ability, fast convergence speed and easy implementation etc. Therefore, in this paper, the nested PSO is used to select the optimal decision variable and uncertain variable of ISVD.

The following parts of this paper is organized as the following. Section 2 reviews the order relation of interval number briefly. Support vector machines are introduced in Section 3, while an ISVD model is proposed in Section 4. Section 5 claims an optimization solver method based on the nested PSO for ISVD. Section 6 analyzes the classification results of UCI data and roller bearing faults, as well as the comparison results with other methods. Finally, the conclusions are presented in Section 7.

2. The theory of order relation

The order relation of interval number is proposed by Ishibuchi et al. [12]. For the minimization optimization problem, order relation ${\le }_{mw}$ of interval number is defined as following:

From Eq. (1), when an interval number $A$ is worse (${\le }_{mw}$) than another interval number $B$, the midpoint $m\left(A\right)$ and the radius $w\left(A\right)$ are bigger than or equal to $m\left(B\right)$ and $w\left(B\right)$;

For maximum optimization problems, Eq. (1) is converted as follows:

Through using ${\le }_{mw}$ to compare the objective function, one can know that the interval of the objective function caused by the uncertainty has not only a small midpoint but also a small radius. Thus, the uncertain objective function can be transformed into a two-objective optimization problem. One objective optimization problem is applied to get the smallest midpoint. The other optimization problem is utilized to obtain the smallest radius [13].

3. The theory of SVM

SVM is a machine learning method which is based on the structured risk minimization. In SVM, the classification can not only separate the two types of samples correctly, but also make the maximum classification distance. The former ensures the minimum of the empirical risk, and the latter is actually to minimize the confidence range. Let $\{\left({\mathbf{x}}_1,y_1\right),\dots ,({\mathbf{x}}_n,y_n\left)\right\}\subset \chi \times R$ be training data. The objective function of SVM can be described as following:

where ${\xi }_j$ is the slack variable, $c$ is the penalty parameter. This optimization problem, including the constraints, can be solved by the Lagrange function as follows:

Computing the partial derivatives, the solution of primal (4) can be calculated by working out the following Wolfe dual problem:

where $a_i$ is Lagrange multiplier. Only those points with $0\le a_i\le C$ are named support vectors.

4. The proposed ISVD optimization model

Through the above treatments, the SVM optimization problem is a quadric program. But when the training sample is an uncertain interval number ${\mathbf{x}}_i=[x_i^L,x_i^R]$, SVM is converted to ISVD model as follows:

where $\mathbf{a}$ is the Lagrange multiplier vector, $\mathbf{x}$ is the uncertain interval samples vector. Through the above order relation ${\le }_{mw}$ in Eq. (1), the optimal interval of the Eq. (6) has a small midpoint and a small radius simultaneously. For this reason, interval support vector optimization model in Eq. (6) can be converted ISVD optimization model. A deterministic two-objective programming problem is presented as:

This two objective programming problem includes the objective function and the constraints. A linear combination method is often used to dispose of the objective function [14]. The penalty function method is used to deal with the constraints [15]. Thus Eq. (7) can be converted into a single objective optimization model with a penalty function:

where 0 $\le \gamma \le$ 1 is a weighting factor of $m\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$ and $w\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$. $\phi$ and $\psi$ are normalization factors, $\sigma$ is the penalty factor which is often set as a large value. Eq. (8) is a nested nonlinear optimization problem. For a Lagrange multiplier vector $\mathbf{a}$, the inner optimization processes are involved to obtain the smallest midpoint and radius for all the uncertain interval samples vector $\mathbf{x}$.

5. Nested PSO based on dynamic decreasing inertia weight for ISVD model

PSO algorithm, different from the genetic algorithm etc., is evolved by the cooperation and competition among individuals but not genetic operators. In the stage of evolution, PSO has many advantages, especially its excellent global optimization ability, simple operation and easy implementation, no selection, crossover, mutation and so on. In order to further improve the global optimization ability of PSO. This paper introduces a modified PSO using dynamically decreasing inertia weight [11]. As mentioned by Shi and Eberhart, when the inertia weight is low ($\omega \text{≤}\text{0.8}$), the search time is very short, that is, all the particles tend to gather together quickly. This confirms that the PSO is more like a local search algorithm when $\omega$ is small. If there is an acceptable solution within the initial search space, then the PSO will find the global optimum quickly, otherwise it will not find the global optimum. On the contrary, when the inertia weight is large ($\omega \text{≥}\text{1.2}$), the PSO algorithm always explores new regions. Of course, the PSO algorithm needs more iteration to reach the global optimal, and it is more likely not to find the global optimal. When the inertia weight is moderate (0.8 $<\omega <$ 1.2), the PSO will have the best chance to find the global optimum but also takes a moderate number of iterations. According to these analyses, Shi and Eberhart do not set the inertia weight as the fixed value, but set it to a function that decreases linearly with time, and the function of the inertia weight is:

The detailed algorithm of PSO based on dynamic decreasing inertia weight can be summarized as follows:

Step 1: Particles are set as the random initial position $x_i^k$, $i=1,\dots ,n_{sw}$ and the random initial velocity $v_i^k$, $i=1,\dots ,n_{sw}$ in the search space.

Step 2: The fitness value is calculated for each particle.

Step 3: Compares each particle with its fitness $f_{id}^k$ and individual extreme $pbes{t}_{id}^k$. If $f_{id}^k>pbes{t}_{id}^k$, $pbes{t}_{id}^k$ is replaced by $f_{id}^k$.

Step 4: updates the velocity and position of each particle according to the following equations:

Step 5: If the end condition is satisfied, the algorithm is exit. Otherwise, $k=k+1$ and go back to Step 2.

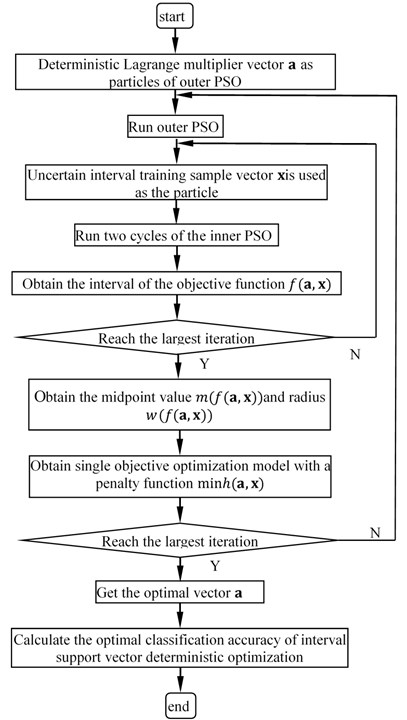
For these advantages of dynamic decreasing inertia weight PSO, a nested PSO is proposed to select the optimal Lagrange multiplier vector $\mathbf{a}$ of Eq. (8). There are two level dynamic decreasing inertia weight PSO in the nested PSO. The outer dynamic decreasing inertia weight PSO (outer PSO) is used to obtain the optimal value of the objective function $\mathrm{m}\mathrm{i}\mathrm{n}h(\mathbf{a},\mathbf{x})$. The deterministic Lagrange multiplier vector $\mathbf{a}$ is used as the particle in this PSO. The inner dynamic decreasing inertia weight PSO (inner PSO) is applied to get the $\underset{\mathbf{x}\in \mathrm{\Gamma }}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$ and $\underset{\mathbf{x}\in \mathrm{\Gamma }}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$. The uncertain training sample vector $\mathbf{x}$ is used as the particle in inner PSO. For computing each interval of the objective function $f(\mathbf{a},\mathbf{x})$, the outer PSO will call for two cycles of the inner PSO. Then the midpoint value $m\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$ and radius of the interval function $w\left(f\right(\mathbf{a},\mathbf{x}\left)\right)$ are calculated. The maximum generations are employed as stopping criterion for nested PSO. This paper draws the flow chart of the nested PSO for interval support vector deterministic optimization model in Fig. 1.

Fig. 1Flow chart of nested PSO for ISVD model

6. The experiment

To check the validity of the proposed ISVD, an UCI data set and the roller bearing fault experiments are carried out in this section.

6.1. The classification of UCI data

In this experiment, UCI iris data [16] set are used to test the effectiveness of ISVD based on nested PSO. Since there is not a set of standard uncertain data set in UCI, this experiment introduces uncertain information on the UCI data sets. The detailed method for adding uncertain information is as follows [17]:

For any UCI samples ${\mathbf{x}}_i=(x_{i1},x_{i2},\dots ,x_{im})$, $i=1,\dots ,n$, one can add the interval uncertain information to each feature vector. The interval feature vector is listed as follows:

10

$\left[{\underset{\_}{x}}_{ij},{\overline{x}}_{ij}\right]=\left[x_{ij}-r_j,x_{ij}+r_j\right],\mathrm{}\mathrm{}i=1,\dots ,n,\mathrm{}\mathrm{}j=\mathrm{1,2},\dots ,m,$

where $r_j$ is the interval radius. It can be obtained is as follows:

11

$r_j=\lambda \frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_{ij}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_{ij}\right)}{20},\mathrm{}\mathrm{}j=\mathrm{1,2},\dots ,m.$

The difference between $\mathrm{m}\mathrm{a}\mathrm{x}\left(x_{ij}\right)$ and $\mathrm{m}\mathrm{i}\mathrm{n}\left(x_{ij}\right)$ indicates the range of the sample set on the dimension $j$. $\lambda$ is a parameter that controls the size of the interval noise. For example: if $\lambda =$ 1, the distribution range of each attribute is added 10 % noise. The interval samples of Iris are shown in Table 1.

Table 1interval samples of iris

Iris type	Sepal length	Sepal width	Petal length	Petal width
Setosa	[5.05, 5.15]	[3.45, 3.55]	[1.38, 1.42]	[0.185, 0.215]
	[4.85, 4.95]	[2.95, 3.05]	[1.38, 1.42]	[0.185, 0.215]
Versicolour	[6.395, 6.605]	[2.75, 2.85]	[4.52, 4.68]	[1.47, 1.53]
	[5.595, 5.805]	[2.75, 2.85]	[4.42, 4.58]	[1.27, 1.33]
Virginica	[6.565, 6.835]	[2.445, 2.555]	[5.695, 5.905]	[1.76, 1.84]
	[7.065, 7.335]	[3.545, 3.655]	[5.995, 6.205]	[2.46, 2.54]

In order to ensure the stability, this paper uses 90 % of cross validation (10-fold Cross validation) estimation. The data sets are randomly divided into 10 groups. One group is taken turns to be chosen as the test set and the other 9 groups as the training set. Averaging 10 times is the result of the final classification accuracy. By using the training set, an interval support vector deterministic optimization is constructed in Eq. (8). In this equation, $\mathbf{x}$ is the interval training samples. $\gamma$ is a weighting factor. The larger $\gamma$ means that the preference of the radius of objection function is increased, while the preference of the midpoint is reduced. In this experiment, $\gamma$ is set 0.5 which means that the radius and midpoint are given a same preference. The proposed interval support vector deterministic optimization based on nested PSO has been implemented in MatLab 2012. The computer owns 3.2G GHz Core (TM)2 i3 CPU and 2.0 G memory. The operation system is Microsoft Windows 7. The detailed information of nested PSO is as follows:

In outer PSO:

(1) Lagrange multiplier vector $\mathbf{a}$ as particle of outer PSO. Number of particles: $n=$ 25;

(2) The largest iteration number: $ite{r}_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 100;

(3) Inertia weight of PSO: ${\omega }_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 1.2, ${\omega }_{\mathrm{m}\mathrm{i}\mathrm{n}}=$ 0.7298;

(4) Positive acceleration constants: $c_1=$ 1.4962, $c_2=$ 1.4962;

In inner PSO, uncertain interval training sample vector $\mathbf{x}$ is used as the particle of inner PSO. The other parameters are the same as the outer PSO. Iris data has three types, but ISVD only aims to tackle two classification problems. For this reason, classification problems of iris data are divided into three groups classification problems. The detailed classification types are: Setosa vs Versicolour, Setosa vs Virginica, Versicolour vs Virginica. The nested PSO runs three times to solve these two classification problems. The convergence result of nested PSO is shown in Fig. 2 and Table 2.

Fig. 2Convergence performance of nested PSO in ISVD

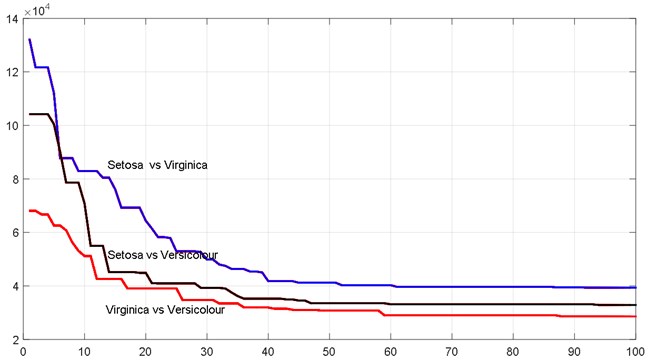
Table 2Optimization results for each two classification problem

–	The interval object function	The midpoint of object function	The radius of object function	The value of penalty function
Setosa vs Versicolour	[5.3715×104, 7.4131×104]	6.3923×104	1.0208×104	2.0125
Setosa vs Virginica	[6.2817×104, 9.8769×104]	8.0793×104	1.7976×104	1.0314
Versicolour vs Virginica	[2.8714×104, 4.9730×104]	3.9222×104	1.0508×104	0.9857

From Fig. 2 and Table 2, it can be found that the iterative solutions of nested PSO can approach the optimum in the 87 iterations. Especially for Setosa vs Virginica, only in 61 iterations, the value of the single objective optimization model combined with midpoint and radius is reduced from 1.265×10⁵ to 4.13×10⁴. Hence, the nested PSO has a higher convergence velocity. Through nested PSO, the optimal Lagrange multiplier vector $\mathbf{a}$ can be obtained and the optimal classification accuracy of ISVD can be calculated finally. The classification accuracy to analyze the performance of the proposed ISVD, NBU1, NBU2 and FBC is demonstrated in Table 3.

Table 3Classification accuracy comparison for Iris

Iris types	NBU1	NBU1	FBC	The proposed ISVD
Setosa	100 %	100 %	100 %	100 %
Versicolour	95 %	95 %	95 %	95 %
Virginica	92.5 %	92.5 %	95 %	97.5 %

According to Table 3, the accuracy of the proposed method is 100 %, 95 %, 97.5 % for Iris Setosa, Iris Versicolour and Iris Virginica respectively. The classification accuracy of the proposed method is 5 % higher than that of NBU1and NBU2 in the Iris Virginica type. For all the three Iris types, the accuracy of the proposed method is 97.5 %. The accuracy of NBU1 and NBU2 is only 95.83 %. Classification accuracy of NBU1 and NBU2 algorithm is the same, which is reasonable since the NBU1 and NBU2 are similar and these two methods are only different in the equation of average value and standard deviation. The accuracy of FBC is 96.67 %. However, as a lazy learning method, FBC needs all training samples to predict each rolling bearing fault repeatedly. Therefore, the memory requirements of this method are too enormous to be offered in fault diagnosis fields. The accuracy of the ISVD is higher than that of NBU1, NBU2 and FBC because the proposed method is constructed based on structured risk minimization theory. This theory pays attention to the empirical risk minimization and the model complexity minimization simultaneously. For this reason, the over fitting problem can be avoided and the proposed method has higher generalization ability for testing samples. Furthermore, based on dynamic decreasing inertia weight, nested PSO can obtain the optimal Lagrange multiplier vector $\mathbf{a}$ and improves the accuracy of ISVD because of its excellent global optimization ability

6.2. Fault diagnosis for the roller bearing

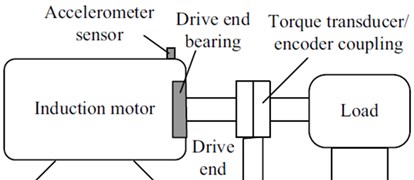
To verify the effectiveness of the proposed method, experiments are carried out on a roller bearing fault test platform in Fig. 3. In this test platform of Case Western Reserve University, an AC motor (2 hp) drives a shaft as the moving output. The corresponding speed of this motor can reach 1730 rpm. The test roller bearing supports the motor shaft at the drive end. The deep groove ball bearing 6205-2RS JEM SKF is selected in the tests platform. Bearing state consists of four categories: normal, inner race fault, outer race fault and ball fault.

Fig. 3a) Motor drive fault test platform, b) schematic diagram of the tests platform

a)

b)

Status of fault damage bearings is a single damage. Damage diameter is divided into 7 mils, 14 mils, 21 mils and 28 mils. The accelerometers are used to collect vibration data. These data can be stored by a recorder at a sampling frequency of 12 kHz for different bearing conditions.

Various defect roller bearing is produced by the electro-discharge machining in this test platform. Different roller bearings, such as inner race fault, outer race fault and ball fault are used to examine the proposed approach. Some defect roller bearing is shown in Fig. 4.

Fig. 4a) outer race fault, b) inner race fault, c) ball fault

a)

b)

c)

Twelve fault types, such as normal bearing, inner race faults whose fault severity are 7 mils, 14 mils, 21 mils and 28 mils, outer race faults whose fault severity are 7 mils, 14 mils, 21 mils, ball faults whose fault severity are 7 mils, 14 mils, 21 mils and 28 mils, are used in this experiment.

6.2.1. Uncertain interval feature vectors acquisition

In this section, each group of bearing fault vibration signal composed of 2048 points, is decomposed by intrinsic time scale decomposition (ITD) method in order to obtain a set of proper rotation components and the base component [18, 19]. The first three groups of rotation component instantaneous amplitude and instantaneous frequency are applied, since they contain the main information. Then, the sample entropy of instantaneous amplitudes and instantaneous frequencies is calculated. Fault data of specific features extraction steps are shown as:

(1) Obtain the fault vibration data from the accelerometers of the fault test platform.

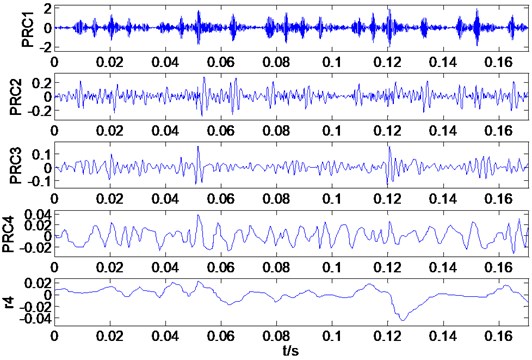
(2) Through ITD decomposition, the fault vibration data is decomposed of a set of rotation components and the baseline component. The decomposition results are given as Fig. 5.

(3) Obtain the first 3 group rotation components instantaneous amplitude, instantaneous frequency and instantaneous frequency.

(4) Calculate the sample entropy of the instantaneous amplitude and instantaneous frequency.

Fig. 5Decomposition results gained by ITD for inner race fault (28 mils)

Each feature vector component is six-dimensional because it includes the sample entropy of the instantaneous phase and instantaneous frequency of the first 3 group rotation components. By this means, 100 samples for each kind of fault signal can be obtained. Since there is no open standard uncertainty rolling bearing fault number set, this experiment also introduces uncertainty information on the rolling bearing fault samples [13]. The detailed method for adding uncertainty information is the same as UCI iris mentioned above.

Then, a part of the training samples and testing samples are shown in Table 4. The amplitude entropy 1 in Table 3 represents the first rotation component instantaneous amplitude sample entropy, other characteristics and so on.

6.2.2. Comparative analysis of classification accuracy

This section uses rolling bearing uncertain interval faults to compare the classification accuracy of NBU1, NBU2, FBC and the proposed method.

In order to ensure the stability of the test results, it is true that 10-fold cross-validation method is also applied to verify the algorithm classification accuracy. Weighting factor of the proposed method $\gamma$ is set 0.5. The experimental results are shown in Table 5. From Table 5, experimental results show that the classification accuracy of the proposed ISVD is better than NBU1, NBU2 and FBC. According to Inner race fault (14mils), accuracy of the proposed ISVD is 6.25 % higher than FBC, NBU1 and NBU2. Moreover, the total accuracy can be calculated. The proposed ISVD: 97.08 %. The reason of such a high accuracy is structural risk minimization principle and the outstanding global optimization ability of nested PSO in the learning process of the proposed method. The accuracy of NBU1is 94.79 %, while the accuracy of NBU2 is 94.58 %. Classification accuracy of NBU1 and NBU2 algorithm based on Naive Bias is very close, which is reasonable since these two methods are constructed based on Naive Bias and only different in the equation of average value and standard deviation. The accuracy of FBC: 95.31 %. However, the FBC algorithm is a kind of lazy learning method. It needs all training samples to predict each rolling bearing fault repeatedly. Both the computational complexity and memory requirements of this method are too large to be offered in roller bearing fault diagnosis.

Table 4Fault samples for twelve kinds of bearing vibration signals

Fault condition	Fault severity	Amplitude entropy 1	Amplitude entropy 2	Amplitude entropy 3	Frequency entropy 1	Frequency entropy 2	Frequency entropy 3
Normal	0	[0.337, 0.381]	[0.169, 0.179]	[0.053, 0.057]	[0.772, 0.797]	[0.323, 0.365]	[0.177, 0.185]
Inner race fault	7	[0.745, 0.756]	[0.423, 0.429]	[0.171, 0.175]	[0.960, 0.967]	[1.058, 1.070]	[0.589, 0.599]
	14	[0.330, 0.340]	[0.392, 0.398]	[0.137, 0.141]	[0.826, 0.837]	[0.921, 0.941]	[0.527, 0.538]
	21	[0.340, 0.347]	[0.302, 0.309]	[0.093, 0.099]	[0.527, 0.534]	[0.676, 0.687]	[0.463, 0.472]
	28	[0.912, 0.925]	[0.309, 0.316]	[0.132, 0.136]	[0.909, 0.917]	[0.730, 0.739]	[0.471, 0.482]
Outer race fault	7	[0.174, 0.179]	[0.385, 0.396]	[0.136, 0.139]	[0.764, 0.776]	[0.833, 0.854]	[0.532, 0.541]
	14	[0.993, 1.010]	[0.359, 0.372]	[0.113, 0.118]	[0.841, 0.852]	[0.823, 0.847]	[0.438, 0.449]
	21	[0.138, 0.143]	[0.225, 0.234]	[0.073, 0.077]	[0.909, 0.918]	[0.674, 0.683]	[0.416, 0.428]
Ball fault	7	[0.908, 0.923]	[0.404, 0.412]	[0.137, 0.141]	[0.652, 0.657]	[0.856, 0.881]	[0.483, 0.491]
	14	[0.722 ,0.778]	[0.390, 0.405]	[0.118, 0.124]	[0.809, 0.829]	[0.878, 0.921]	[0.489, 0.504]
	21	[0.834, 0.889]	[0.441, 0.450]	[0.158, 0.162]	[0.797, 0.810]	[0.944, 0.963]	[0.536, 0.551]
	28	[0.407, 0.434]	[0.463, 0.476]	[0.176, 0.181]	[0.593, 0.600]	[1.137, 1.150]	[0.579, 0.590]

Table 5Classification accuracy comparison of four algorithms

Fault condition	Target output	The proposed method	FBC	NBU1	NBU2
Normal	1	100 %	100 %	100 %	100 %
Ball (7mils)	2	100 %	100 %	93.75 %	93.75 %
Inner race fault (7mils)	3	100 %	100 %	100 %	100 %
Outer race fault (7mils)	4	100 %	100 %	98.75 %	98.75 %
Ball (14mils)	5	71.25 %	62.5 %	67.5 %	65 %
Inner race fault (14mils)	6	100 %	93.75 %	93.75 %	93.75 %
Outer race fault (14mils)	7	98.75 %	97.5 %	97.5 %	97.5 %
Ball (21mils)	8	95 %	91.25 %	90 %	90 %
Inner race fault (21mils)	9	100 %	100 %	100 %	100 %
Outer race fault (21mils)	10	100 %	100 %	100 %	100 %
Ball (28mils)	11	100 %	100 %	100 %	100 %
Inner race fault (28mils)	12	100 %	98.75 %	96.25 %	96.25 %

7. Conclusions

In this paper, ISVD is proposed by incorporating the interval number order relation theory into SVM, so that the advantages of SVM can be preserved. The main advantage is that the structural risk minimization principle enables the proposed method to generalize well in the unseen interval testing samples. Moreover, outstanding global optimization ability of nested PSO further improves the classification effect of the proposed method. Experiment results show that the proposed method has higher classification accuracy in roller bearing interval fault than NBU1, NBU2 and FBC. Nowadays, ISVD is still in the experimental verification stage based on the motor drive fault test platform. The proposed method will be used in the actual working environment. Its ability to resist noise needs further improvement in the near future, which will be the following important task of this research team