Design and simulation analysis of an improved wearable power knee exoskeleton

Wang, Fangzheng; Yan, Lei; Xiao, Jiang; Fan, Lei

doi:10.21595/jve.2019.19920

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2019

Check for updates

Design and simulation analysis of an improved wearable power knee exoskeleton

Fangzheng Wang¹

Lei Yan²

Jiang Xiao³

Lei Fan⁴

^{1, 2, 3, 4}School of Technology, Beijing Forestry University, Beijing, China

Corresponding Author:

Lei Yan

Cite the article Download PDF

Downloads 1765

WoS Core Citations 5

CrossRef Citations 5

Abstract

The wearable lower limb power robotic exoskeleton is a device that can improve the human walking ability. In this paper, an improved exoskeleton device for knee joint is designed, including the improvement of mechanical structure and hydraulic cylinder. In order to verify the effectiveness of the improvement of the hydraulic cylinder, we have carried out the following studies. Firstly, in terms of mechanical structure, length adjusting device is added to meet the needs of different people. At the same time, a limit device is added to the knee joint to improve the safety performance and comfort. Secondly, the dynamics of the model is carried out by Lagrange, and the exoskeleton model is established for ADAMS motion simulation. The force of ADAMS simulation, the calculated by Lagrange equation and the force of the first edition of hydraulic cylinder are compared, and the force selection of hydraulic cylinder is analyzed. By comparison with the first edition, the optimization rate of the improved hydraulic cylinder reaches 8 %. Finally, in order to verify the rationality of ADAMS simulation and the effectiveness of hydraulic cylinder improvement, the wear test is carried out, the average errors of leg centroid in normal walking, wearing exoskeleton walking and ADAMS simulation data are compared. The average error rate is less than 10 %. The results show that the simulation model design is reasonable, and the effectiveness of the hydraulic cylinder improvement is verified. The exoskeleton device designed can well follow the human motion. The simulation analysis of the exoskeleton provides important parameters for the manufacture and it also provides theoretical basis for the later control theory.

Design and simulation analysis of an improved wearable power knee exoskeleton

Highlights

Structure design of an improved wearable power knee exoskeleton
Adams simulation
Wear walking experiments

1. Introduction

The wearable exoskeleton device has been widely used in all aspects of daily life and industry. For example, in military applications, an exoskeleton is mainly used to improve the operational ability of soldiers and ease the carrying of weapons [1]. In industrial applications, the exoskeletons are mainly used to reduce the labor intensity of workers. In addition, in the medical field, an exoskeleton can assist patients who are unable to walk [2]. However, some important factors, such as lightness quality, wear comfort and control flexibility, need to be improved.

A brief introduction of a few commercial exoskeleton robot is presented below.

The AlterG Bionic Leg™ is a wearable mobile auxiliary device, which is powered by batteries [3]. It can help patients walk and automatically identify the patients' movement intention [4, 5]. At the same time, the device can also help in the rehabilitation of patients with spinal injuries to help them walk, so as to enhance and improve their sports posture and enhance their ability to exercise.

The C-Brace® Orthotronic Mobility System is a passive knee ankle foot orthosis robotic exoskeleton for running support [6]. It can be used to help paralyzed patients recover by stretching the knee joint. The hydraulic resistance control is provided by adjusting the hydraulic resistance of the standing stage and the swing stage to provide the walking aid to the patients, help wearers run or climb stairs to satisfy the patients’ walking desire [7, 8].

A robotic knee exoskeleton robot has been designed in our Laboratory for the assistance of the elderly. The first version of the lower limb exoskeleton was designed, as shown in Fig. 1. However, some shortcomings in the trial restricted the cooperation ability of the robot with the patient, the structure was heavy, the operation was inconvenient, and the security was poor. Therefore, in this paper, the improved version is introduced. In order to verify the effectiveness of the hydraulic cylinder improvement, the dynamic analysis of the model is carried out by Lagrange, and the ADAMS motion simulation of the exoskeleton model is established. By comparison with the first edition, the optimization rate of the improved hydraulic cylinder reaches 8 %. In order to verify the rationality of ADAMS simulation and the effectiveness of hydraulic cylinder improvement, the wear test was carried out. The average errors of the center of mass of the legs in normal walking, wearing exoskeleton walking and ADAMS simulation data were compared, and the average error rate was less than 10 %. The results show that the simulation model design is reasonable and the effectiveness of the improvement of the hydraulic cylinder is verified.

Fig. 1The first version of the knee joint powered robotic exoskeleton

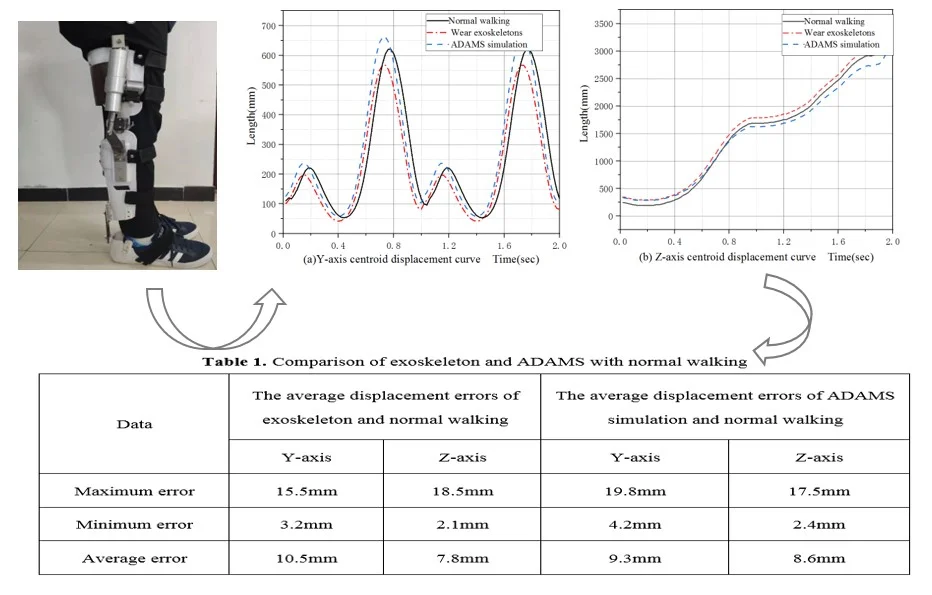
Fig. 2The improved version of the robotic exoskeleton

2. The structure design of lower limb exoskeleton

The robotic exoskeleton is a device that combines a human with a machine. The improved version is diagrammatically depicted in Fig. 2, the knee joint of the lower extremities has one degree of freedom, and an actuator. The device was ergonomically designed for the comfort and convenience of the wearer. The structure of the whole device is optimized and improved to increase its quality. In addition, an adjustable device is used on the thighs and legs in order to meet the wear ability requirements of patients with different heights.

2.1. The length adjusting of the device

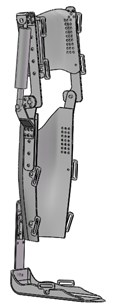
In order to wear more comfortably, the design of exoskeleton should be consistent with the size of human lower limbs, and the length of exoskeleton device can be adjusted according to the requirements. Fig. 3 shows the proportion of lower limbs relative to the total height of the human body. Let $H$ be the total height of the human body, the total height of the thigh relative to the human body is 0.245 $H$ , and the length of the leg relative to the human body is 0.246 $H$ [9]. As shown in Fig. 3, the red line represents the position of the lower extremity exoskeleton device in the human body. The total length of the designed thigh relative to the human body is 0.12 $H$ , and the length of the lower leg relative to the human body is 0.246 $H$ . According to the height range from 160 cm to 180 cm, for example. As shown in Table 1, the adjusting lengths of the thighs and legs of the exoskeleton device are calculated when $H =$ 160 cm and $H =$ 180 cm [10].

According to Table 1, the structural parameters of the rod of exoskeleton device are determined:

• Adjustment range of thigh: 190 mm-220 mm,

• Adjustment range of calf: 390 mm-450 mm.

Fig. 3The body with the height of the proportion

Table 1Adjustment range of connecting rod of exoskeleton robot

Connecting rod	$H$	1600 mm	1800 mm	Range
Length of thigh	0.12 $H$	190 mm	220 mm	190 mm-220 mm
Length of the calf	0.246 $H$	390 mm	450 mm	390 mm-450 mm

Four adjusting holes are designed by adjusting device. The adjusting interval of thigh is 10 mm, so the length of thigh can be fixed to 190 mm, 200 mm, 210 mm and 220 mm. The adjusting interval of calf is 20 mm, so the length of the calf can be fixed to 390 mm, 410 mm, 430 mm and 450 mm. The position of the adjusting hole is shown in Fig. 4.

Fig. 4a) The adjusting device of the length of the thigh, b) the adjusting device of the length of the calf

a)

b)

2.2. The limiting device of the knee

When designing the exoskeleton, careful consideration should be given to safety issues. Accordingly, a knee joint rotation limiting device is necessary to include in the design. In the direction of sagittal movement, the rotation range of the knee joint is between 0-80° [3, 11]. In order to avoid the knee joint going beyond this range, we designed a groove in the knee joint rotation device, so the exoskeleton can only move within this range, as shown in Fig. 5(a). Its working principle is shown in Fig. 5(b). When the knee joint rotates, points A and B rotate around the center point O in the groove mechanism respectively. When A rotates to C and B rotates to D, they reach the ultimate rotation position, which helps to realize the limitation of the range of motion of the joint, so as to play a role in human safety protection.

Fig. 5Knee joint rotation limiting device

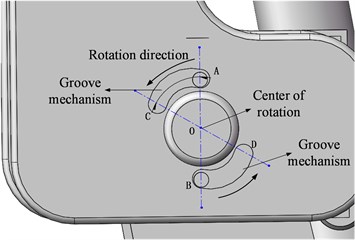
a) Working sketch

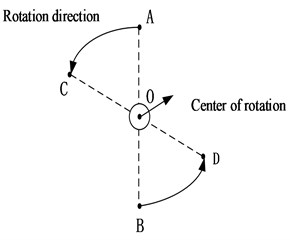
b) Working principle diagram

2.3. The driving mechanism

The exoskeleton device not only needs to be small in size and have a compact structure, but also must be lightweight. Therefore, the actuator uses an electric hydraulic cylinder, as shown in Fig. 6. First, the hydraulic actuator is a linear motion actuator, which greatly simplifies the design of the mechanical structure, and can transform mechanical energy into human motion and provide assistance. Second, it is small in size and smooth motion, making the whole structure more compact and natural [12, 13]. The rod parts of the hydraulic actuating structure were theoretically analyzed. Through calculation, the normal rated thrust of the hydraulic cylinder is is 600 N.

Fig. 6Knee driving linear motion actuator with hydraulic cylinder and hydraulic cylinder motion diagram

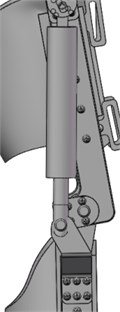
a)

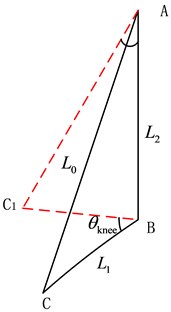
b)

As shown in Fig. 6, to establish the relationship between the hydraulic cylinder and the installation location:

1

θ = ∠ A B C - θ_{k n e e} .

$θ$ Comprises two straight lines $L_{1}$ and $L_{2}$ angle type, among them, the $L_{1}$ length is 38 mm and $L_{2}$ length is 189 mm. $θ_{k n e e}$ is the knee joint angle

In the case of the cosine law $△ A B C$ , the length of the driver can be obtained:

2

L_{0} = \sqrt{L_{1}^{2} + L_{2}^{2} - 2 L_{1} L_{2} c o s θ} .

However, the length of the drive must meet the Eq. (3) below:

3

L_{m i n} \leq L_{0} \leq (L_{m i n} + d),

when the knee joint hydraulic cylinder is at the two limit positions, the journey is the largest. According to human kinematics parameters, the rotation range of human knee joint is 0-80° [14], with 0 and 80 generation into the type (2). The length of the hydraulic cylinder change range was calculated to be from 195 mm-220 mm, with the largest travel distance being 25 mm. The maximum driving torque of the walking aid mechanism should be the same as that of the driving body. The average weight of the normal human body is 60 kg [7, 15]. The proportion of the human body lower limbs relative to the whole human body is 38.68 % [16]:

4

T_{1} = m \times 38.68 % \times t \times 1000 = 60 \times 38.68 % \times 0.98 \times 1000 = 22743.84 N . m m .

Among them, $t$ is the unit joint moment, the value is 0.98 N/kg. Finding the Maximum Driving Torque $T_{1}$ , According to the Eq. (5):

5

T_{1} = F_{1} . L_{1} .

Given the lengths of the maximum driving torques $T_{1}$ and $L_{1}$ , the maximum pulling force at the knee joint can be calculated. as follows the Eq. (6):

6

F_{1} = \frac{T_{1}}{L_{1}} = \frac{22743.84}{38} = 598.52 N .

Accordingly, the selected driving force of the hydraulic cylinder is 600 N.

3. Lower limb exoskeleton dynamics analysis and simulation

In order to verify the practicality of the design of the hydraulic cylinders and the mechanisms, the Lagrange method is adopted, and a simulation is conducted using the ADAMS software.

3.1. Dynamics analysis

First, in the process of dynamic analysis, we use Lagrange multipliers for dynamic analysis based on Fig. 9. The Lagrange equation is as shown in Eq. (7) and Eq. (8):

7

τ_{i} = \frac{d}{d_{t}} (\frac{\partial L}{\partial \overset{•}{q_{i}}}) - \frac{\partial L}{\partial q_{i}}, (i = 1,2, \dots, n),

8

L = E_{K} - E_{P} .

Therefore, the formulas to calculate the kinetic energy and the potential energy are as shown below.

Thigh connecting rod is as shown in Eq. (9) and Eq. (10):

9

E_{k 1} = \frac{1}{2} (m_{1} + M_{1}) l_{c 1}^{2} {\dot{θ}}_{1}^{2} - \frac{1}{2} m_{a} l_{c 1}^{2} {\dot{θ}}_{1}^{2},

10

E_{P 1} = (m_{1} + M_{1}) g l_{c 1} c o s θ_{1} - m_{a} g l_{1} c o s θ_{1} .

The crus connecting rod is as shown in Eq. (11) and Eq. (12):

11

E_{k 2} = \frac{1}{2} (m_{2} + M_{2}) [l_{c 1}^{2} {\dot{θ}}_{1}^{2} + l_{c 2}^{2} ({\dot{θ}}_{1} + {\dot{θ}}_{2})^{2} - 2 l_{1} l_{c 1} ({\dot{θ}}_{1} + {\dot{θ}}_{2}) {\dot{θ}}_{1} c o s {\dot{θ}}_{2}],

12

E_{P 2} = (m_{2} + M_{2}) g [- l_{1} c o s θ_{1} + l_{c 2} \cos (θ_{1} + θ_{2})] .

The expression of the Lagrange function can be obtained from the above formulas, as shown in Eq. (13):

13

L = E_{K 1} + E_{K 2} - (E_{P 1} + E_{P 2}) .

In the calculation, we can assume that the ankle as a passive joint, which rotates with the rotation of the knee joint. Accordingly, we can consider the following part of the knee joint as a whole connecting rod, and the unilateral robotic exoskeleton model can be simplified as a two-link model, as follows Eq. (14) and Eq. (15):

14

\begin{array}{l} E_{K 2} = \frac{1}{2} (m_{2} + M_{2}) [l_{c 1}^{2} {\dot{θ}}_{1}^{2} + l_{c 2}^{2} ({\dot{θ}}_{1} + {\dot{θ}}_{2})^{2} - 2 l_{1} l_{c 1} ({\dot{θ}}_{1} + {\dot{θ}}_{2}) {\dot{θ}}_{1} c o s {\dot{θ}}_{2}] \\ + \frac{1}{2} m_{f} [l_{c 1}^{2} {\dot{θ}}_{1}^{2} + l_{c 2}^{2} ({\dot{θ}}_{1} + {\dot{θ}}_{2})^{2} - 2 l_{1} l_{c 1} ({\dot{θ}}_{1} + {\dot{θ}}_{2}) {\dot{θ}}_{1} c o s {\dot{θ}}_{2}], \end{array}

15

\begin{matrix} E_{P 2} = (m_{2} + M_{2}) g [- l_{1} c o s θ_{1} + l_{c 2} \cos (θ_{1} + θ_{2})] + m_{f} g [- l_{1} c o s θ_{1} + l_{c 2} \cos (θ_{1} + θ_{2})] . \end{matrix}

The Lagrange function of the single side two-link system of the mechanism $L$ is as shown in Eq. (16):

16

L = E_{K 1} + E_{K 2} - (E_{P 1} + E_{P 2}) = \frac{1}{2} (m_{1} + M_{1}) l_{c 1}^{2} {\dot{θ}}_{1}^{2} - \frac{1}{2} m_{a} l_{c 2}^{2} {\dot{θ}}_{1}^{2}

+ \frac{1}{2} (m_{1} + M_{1}) [l_{c 1}^{2} {\dot{θ}}_{1}^{2} + l_{c 1}^{2} ({\dot{θ}}_{2} + {\dot{θ}}_{1})^{2} - 2 l_{1} l_{c 1} ({\dot{θ}}_{2} + {\dot{θ}}_{1}) {\dot{θ}}_{1} c o s {\dot{θ}}_{2}]

+ \frac{1}{2} m_{f} [l_{c 1}^{2} {\dot{θ}}_{1}^{2} + l_{c 2}^{2} ({\dot{θ}}_{2} + {\dot{θ}}_{1})^{2} - 2 l_{1} l_{c 1} ({\dot{θ}}_{2} + {\dot{θ}}_{1}) {\dot{θ}}_{1} c o s {\dot{θ}}_{2}] + (m_{1} + M_{1}) g l_{c 1} c o s θ_{1}

- m_{a} g l_{1} c o s θ_{1} - (m_{2} + M_{2}) g [- l_{1} c o s θ_{1} + l_{c 2} \cos (θ_{2} + θ_{1})]

- m_{f} g [- l_{1} c o s θ_{1} + l_{c 2} \cos (θ_{2} + θ_{1})] .

According to the above formula, we need to take the derivative respectively:

\frac{\partial L}{\partial θ_{1}}, \frac{\partial L}{\partial θ_{2}}, \frac{\partial L}{\partial {\dot{θ}}_{1}}, \frac{\partial L}{\partial {\dot{θ}}_{2}}, \frac{d}{d_{t}} \frac{\partial L}{\partial {\dot{θ}}_{1}}, \frac{d}{d_{t}} \frac{\partial L}{\partial {\dot{θ}}_{2}} .

The dynamic expression of the torque of the hip joint $T_{1}$ and the torque of the knee joint $T_{2}$ is as shown in Eq. (17) and Eq. (18):

17

T_{1} = D_{11} {\ddot{θ}}_{1} + D_{12} {\ddot{θ}}_{2} + D_{111} {\dot{θ}}_{1} + D_{122} {\dot{θ}}_{2} + D_{112} {\dot{θ}}_{1} {\dot{θ}}_{2} + D_{121} {\dot{θ}}_{2} {\dot{θ}}_{1} + D_{1},

18

T_{2} = D_{21} {\ddot{θ}}_{1} + D_{22} {\ddot{θ}}_{2} + D_{211} {\dot{θ}}_{1} + D_{222} {\dot{θ}}_{2} + D_{212} {\dot{θ}}_{1} {\dot{θ}}_{2} + D_{221} {\dot{θ}}_{2} {\dot{θ}}_{1} + D_{2} .

The equations of $T_{1}$ and $T_{2}$ expressed in matrix form are as shown in Eq. (19):

19

[\begin{array}{l} T_{1} \\ T_{2} \end{array}] = [\begin{array}{l} D_{11} & D_{12} \\ D_{21} & D_{22} \end{array}] [\begin{array}{l} {\ddot{θ}}_{1} \\ {\ddot{θ}}_{2} \end{array}] + [\begin{array}{l} D_{111} & D_{122} \\ D_{211} & D_{222} \end{array}] [\begin{array}{l} {\dot{θ}}_{1} \\ {\dot{θ}}_{2} \end{array}] + [\begin{array}{l} D_{112} & D_{121} \\ D_{212} & D_{221} \end{array}] [\begin{array}{l} {\dot{θ}}_{1} {\dot{θ}}_{2} \\ {\dot{θ}}_{2} {\dot{θ}}_{1} \end{array}] + [\begin{array}{l} D_{1} \\ D_{2} \end{array}] .

Through the above calculations, we provide a reliable theoretical basis for the motion state of the single lower extremity robotic exoskeleton, and provide a reference for the selection of hydraulic cylinders. In addition, the calculations also provide a theoretical basis and reference for the development and design of the control system.

3.2. Adams simulation analysis

For the purposes of the simulation, the three-dimensional model fabricated using SolidWorks is imported into the ADAMS software [17, 18]. The properties need to be edited, so the length and the center of gravity of each component in the ADAMS software, and the parameters are set up as shown in Table 2.

Table 2Normal human body size and quality

The section name of the body	Mass or centroid (mean value)	Length
Calf	2.20 kg	344 mm
Calf	224.1 mm	344 mm
Thigh	8.50 kg	438 mm
Thigh	254.5 mm	438 mm
Torso	26.37 kg	466.8 mm
Upper arm	1.46 kg	284 mm
Fore arm	0.75 kg	213 mm

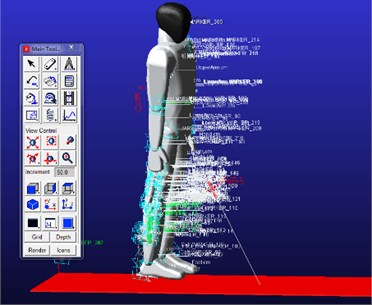
In the simulation process, we need to limit the rotation of the upper part of the human body to maintain balance. The friction coefficient is 0.6 in the human body and the ground [19, 20]. The driving data of each joint is set according to the standard drive function. The model is depicted in Fig. 7.

Fig. 7Wearable exoskeleton model and the human body

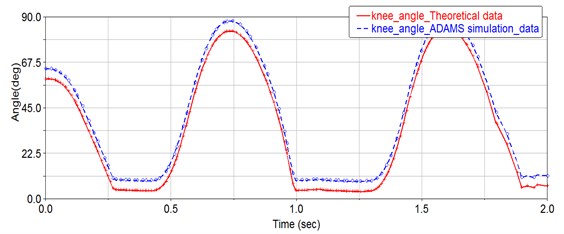
After the simulation, the data processing is performed by the ADAMS/postprocessor. As shown in Fig. 8, it is the theoretical angle of knee exoskeleton rotation and the angle data of ADAMS simulation. From the analysis of simulation data, it is found that the rotation angle of human knee joint is between 0 and 80 degrees, and it changes periodically. Through comparison, the error between simulation data and theoretical angle is within 0-6 degrees range, which shows that the simulation data of human joint angle accords with human kinematics. In addition, through the simulation data, it can be seen that the design of the knee joint limitation device meets the actual needs.

Fig. 8Knee joint angle and the rotation angle of the Adams simulation

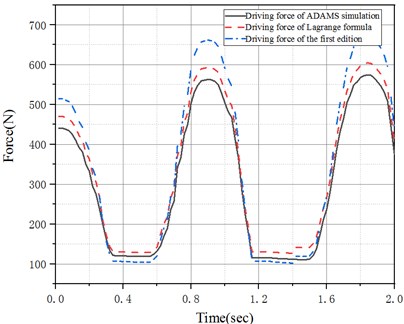
As shown in Fig. 9, three force curves are compared, including the hydraulic cylinder driving force simulated by ADAMS, the hydraulic cylinder driving force of the first edition and the Lagrange dynamic theory analysis. In Fig. 9, it can be concluded that the driving force trends of the three cylinders are similar and have good consistency. For the driving force of knee joint, the calculated moment of Lagrange equation is in good agreement with the driving force obtained by ADAMS simulation, which proves the correctness of the theoretical analysis of Lagrange dynamics. The maximum driving force of the hydraulic cylinder simulated by ADAMS is 560 N, and the maximum driving force of the hydraulic cylinder in the first edition is 650 N. Using ADAMS simulation data as standard, the average error of Lagrange is 10 N, the average error of driving force of the first edition is 50 N, and the optimal driving force of the selected hydraulic cylinder is 8 %.

Fig. 9Knee hydraulic cylinder driving force

4. Results verification

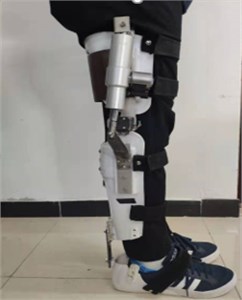
In order to verify the rationality of ADAMS simulation and the effectiveness of hydraulic cylinder improvement. The wear comparison experiment is needed. The influence of exoskeleton on human walking gait is mainly a comparative analysis of gait data with periodic variation. In this experiment, we used the data of human normal walking, wearing exoskeleton walking and ADAMS simulation to analyze the displacement curves in the $Y$ and $Z$ axis of the sagittal knee joint. As shown in Fig. 10, it is the human walking test with wearing exoskeleton.

Fig. 10The human walking test with wearing exoskeleton

As shown in Fig. 11, it is the change curve of center of mass displacement in $Y$ and $Z$ directions of normal walking, wearing exoskeleton walking and ADAMS simulation, and there is good consistency between them. The $Y$ direction represents the vertical displacement and the $Z$ direction represents the forward displacement.

Fig. 11Comparison of centroid changes of Y and Z axis

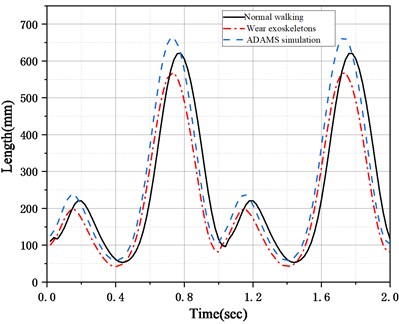
a) $Y$ -axis centroid displacement curve

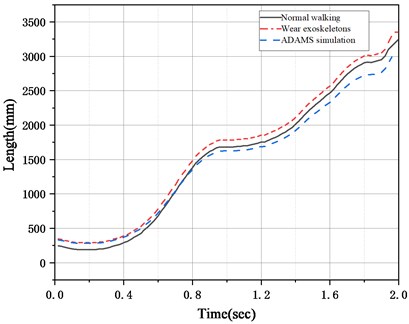
b) $Z$ -axis centroid displacement curve

Using the normal walking data as the standard, as shown in Table 3, the average displacement errors of exoskeleton and normal walking in $Y$ -axis is 10.5 mm, the average displacement errors of exoskeleton and normal walking in $Z$ -axis is 7.8 mm. The average displacement errors of ADAMS simulation and normal walking in $Y$ -axis is 9.3 mm, the average displacement errors of ADAMS simulation and normal walking in $Z$ -axis is 8.6 mm. The average error is less than 10 %, the average error is within the required accuracy range. The results show that the ADAMS simulation model is reasonable, and the dynamic model can meet the requirements, which verifies the effectiveness of hydraulic cylinder improvement.

Table 3Comparison of exoskeleton and ADAMS with normal walking

Data	The average displacement errors of exoskeleton and normal walking		The average displacement errors of ADAMS simulation and normal walking
Data	$Y$ -axis	$Z$ -axis	$Y$ -axis	$Z$ -axis
Maximum error	15.5 mm	18.5 mm	19.8 mm	17.5 mm
Minimum error	3.2 mm	2.1 mm	4.2 mm	2.4 mm
Average error	10.5 mm	7.8 mm	9.3 mm	8.6 mm

5. Conclusions

In this paper, an improved exoskeleton device for knee joint is designed, including the improvement of mechanical structure and hydraulic cylinder. In terms of mechanical structure, adjusting device and safety limit device are added. In order to verify the effectiveness of the hydraulic cylinder improvement, the dynamic analysis of the model is carried out by Lagrange, and the ADAMS simulation of the exoskeleton model is established. Three force curves were compared, including the force of ADAMS simulation, the calculated by Lagrange equation and the force of the first edition of hydraulic cylinder. Using the data simulated by ADAMS as the standard, the optimal driving force of the selected hydraulic cylinder was 8 %. In order to verify the rationality of ADAMS simulation and the effectiveness of hydraulic cylinder improvement, the wear test was carried out. The average error rate is less than 10 %. Therefore, the results show that the ADAMS simulation model is reasonable, and the dynamic model can meet the requirements, which verifies the effectiveness of hydraulic cylinder improvement. It also provides theoretical basis for the later control theory.

References

Vital J. P., et al. Combining discriminative spatiotemporal features for daily life activity recognition using wearable motion sensing suit. Pattern Analysis and Applications, Vol. 20, Issue 4, 2017, p. 1179-1194.

Publisher
Witte K. A., Fatschel A. M., Collins S. H. Design of a lightweight, tethered, torque-controlled knee exoskeleton. International Conference on Rehabilitation Robotics, London, 2017.

Publisher
Lu R., Li Z., Su C. Y., Xue A. Development and learning control of a human limb with a rehabilitation exoskeleton. IEEE Transactions on Industrial Electronics, Vol. 61, Issue 7, 2014, p. 3776-3785.

Publisher
Horst R. W. A bio-robotic leg orthosis for rehabilitation and mobility enhancement. Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2009.

Publisher
Xiao Y., Wang X., Li Z., Zhao Y. A method of kinematic analysis and singularity elimination for upper-limb exoskeleton. Jiqiren/Robot, Vol. 38, Issue 1, 2016, p. 33-40.

Search CrossRef
Xu X., Hou L., Huang X., Zhang W. Design and research of a wearable robot for upper limbs rehabilitation based on exoskeleton. Jiqiren/Robot, Vol. 36, Issue 2, 2014, p. 147-155.

Search CrossRef
Bai K. Design of a compliant knee-motion actuator for lower extremity exoskeletons. IEEE International Conference on Advanced Intelligent Mechatronics, Canada, 2016.

Publisher
Shamaei K., et al. Biomechanical effects of stiffness in parallel with the knee joint during walking. IEEE Transactions on Biomedical Engineering, Vol. 62, Issue 10, 2015, p. 2389-2401.

Publisher
Kirsch N. A., et al. Model-based dynamic control allocation in a hybrid neuroprosthesis. IEEE Transactions on Neural Systems and Rehabilitation Engineering, Vol. 26, Issue 1, 2018, p. 224-232.

Publisher
Yin Y. H., Fan Y. J., Xu L. D. Emg and Epp-integrated human-machine interface between the paralyzed and rehabilitation exoskeleton. IEEE Transactions on Information Technology in Biomedicine, Vol. 16, Issue 4, 2012, p. 542-549.

Publisher
Dollar A., Herr H. Lower extremity exoskeletons and active orthoses: challenges and state of the art. IEEE Transactions on Robotics, Vol. 24, Issue 1, 2008, p. 144-158.

Publisher
Martínez A., Lawson B., Goldfarb M. A Controller for guiding leg movement during overground walking with a lower limb exoskeleton. IEEE Transactions on Robotics, Vol. 34, Issue 1, 2018, p. 183-193.

Publisher
Lerner Z. F., Damiano D. L., And Bulea T. C. Relationship between assistive torque and knee biomechanics during exoskeleton walking in individuals with crouch gait. International Conference on Rehabilitation Robotics, London, 2017.

Publisher
Azocar A. F., Rouse E. J. Stiffness perception during active ankle and knee movement. IEEE Transactions on Biomedical Engineering, Vol. 64, Issue 12, 2017, p. 2949-2956.

Publisher
Viteckova S., Kutilek P., Jirina M. Wearable lower limb robotics: a review. Biocybernetics and Biomedical Engineering, Vol. 33, Issue 2, 2013, p. 96-105.

Publisher
Kim J. H., Han J. W., Kim D. Y., et al. Design of a walking assistance lower limb exoskeleton for paraplegic patients and hardware validation using CoP. International Journal of Advanced Robotic Systems, Vol. 10, Issue 9, 2013, p. 113-126.

Publisher
Hussain S., Xie S. Q., Jamwal P. K. Control of a robotic orthosis for gait rehabilitation. Robotics and Autonomous Systems, Vol. 61, Issue 9, 2013, p. 911-919.

Publisher
Anam K., Al-Jumaily A. Active exoskeleton control systems: state of the art. Procedia Engineering, Vol. 41, Issue 2, 2012, p. 988-994.

Publisher
Miao Y., Gao F., Pan D. State classification and motion description for the lower extremity exoskeleton SJTU-EX. Journal of Bionic Engineering, Vol. 11, Issue 2, 2014, p. 249-258.

Publisher
Shamaei K., Napolitano P. C., Dollar A. M. A quasi-passive compliant stance control Knee-Ankle-Foot Orthosis. IEEE 13th International Conference on Rehabilitation Robotics, Washinggton, 2013.

Publisher

Cited by

Design of a personalized knee rehabilitation exoskeleton with high motion compliance

(2024)

User experience of lower extremity exoskeletons and its improvement methodologies: A narrative review

Yuan Zhou

(2024)

2022 IEEE International Conference on Real-time Computing and Robotics (RCAR)

(2022)

Weight Distribution of a Knee Exoskeleton Influences Muscle Activities During Movements

Yi-Xing Liu | Longbin Zhang | Ruoli Wang | Christian Smith | Elena M. Gutierrez-Farewik

(2021)

Knee Exoskeletons Design Approaches to Boost Strength Capability: A Review

Juan R. Meda-Gutiérrez | Luis Adrián Zúñiga-Avilés | Adriana H. Vilchis-González | Juan Carlos Ávila-Vilchis

(2021)

About this article

Received

23 April 2018

Accepted

24 April 2019

Published

15 August 2019

SUBJECTS

Biomechanics and biomedical engineering

DOI

https://doi.org/10.21595/jve.2019.19920

Keywords

knee joint exoskeleton

dynamics analysis

Adams simulation

Acknowledgements

This study is financially supported by the Fundamental Research Funds for the Central Universities (No. 2015ZCQ-GX-03).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 09 21

A new driving strategy for Lower limb-assisted exoskeleton robot

Jin Zhu, Qi Huang, Xuan Li, Xiaojun Zhou

Research article

2022 05 15

Research on intelligent prosthetic knee system

Xinxin Deng, Zhiming Wang

Research article

2017 06 30

Study on the control algorithm for lower limb exoskeleton based on ADAMS/Simulink co-simulation

Hongfang Wu, Tianyu Jia, Na Li, Jian Wu, Lei Yan

Research article

2016 12 31

Optimization of the control scheme for human extremity exoskeleton

Yang Li, Cheng Xu, Xiaorong Guan, Zhong Li

F. Wang, L. Yan, J. Xiao, and L. Fan, “Design and simulation analysis of an improved wearable power knee exoskeleton,” Journal of Vibroengineering, Vol. 21, No. 5, pp. 1472–1482, Aug. 2019, https://doi.org/10.21595/jve.2019.19920

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.19920
UR  - https://doi.org/10.21595/jve.2019.19920
TI  - Design and simulation analysis of an improved wearable power knee exoskeleton
T2  - Journal of Vibroengineering
AU  - Yan, Lei
AU  - Wang, Fangzheng
AU  - Xiao, Jiang
AU  - Fan, Lei
PY  - 2019
DA  - 2019/08/15
PB  - JVE International Ltd.
SP  - 1472-1482
IS  - 5
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Yan_2019,
	doi = {10.21595/jve.2019.19920},
	url = {https://doi.org/10.21595/jve.2019.19920},
	year = 2019,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {5},
	pages = {1472--1482},
	author = {Lei Yan and Fangzheng Wang and Jiang Xiao and Lei Fan},
	title = {Design and simulation analysis of an improved wearable power knee exoskeleton},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. Yan, F. Wang, J. Xiao, and L. Fan, “Design and simulation analysis of an improved wearable power knee exoskeleton,” Journal of Vibroengineering, vol. 21, no. 5, pp. 1472–1482, Aug. 2019, doi: 10.21595/jve.2019.19920.

Copy IEEE

Copied to clipboard!

Yan, Lei, Fangzheng Wang, Jiang Xiao, and Lei Fan. “Design and Simulation Analysis of an Improved Wearable Power Knee Exoskeleton.” Journal of Vibroengineering 21, no. 5 (August 15, 2019): 1472–82. https://doi.org/10.21595/jve.2019.19920.

Copy Chicago

Copied to clipboard!

Design and simulation analysis of an improved wearable power knee exoskeleton

Abstract

Highlights

1. Introduction

2. The structure design of lower limb exoskeleton

2.1. The length adjusting of the device

2.2. The limiting device of the knee

2.3. The driving mechanism

3. Lower limb exoskeleton dynamics analysis and simulation

3.1. Dynamics analysis

3.2. Adams simulation analysis

4. Results verification

5. Conclusions

References

Cited by

About this article

Related Articles