Study on applicability of end corrections of extended inlet and outlet of expansion chamber hydraulic noise suppressor

2.1. Method

When the noise frequency is lower than the cut-off frequency of a muffler, the plane wave theory can be used to analyze the filtering characteristics [1]. In order to apply this theory to the analysis of acoustic characteristics of hydraulic suppressors, the following assumption was made [1, 2, 13]:

1. The hydraulic oil in the pipeline has laminar flow without tangential velocity component.

2. Compared with the environmental state, pressure pulsation is regarded as a small amplitude disturbance and the Mach number is very low. Therefore, the mean flow can be neglected. Also, compared with the density of the medium, perturbations on density are very small.

3. Compared with the pipe diameter, the pipeline is longer, so the effect of the end point can be ignored.

4. The time dependence is assumed to be of the exponential form $e^{j\omega t}$ where $\omega$ is the angular frequency.

According to the above hypotheses, the 1D wave equation admits a general solution [1]:

and therefore:

where $p$ is the fluctuating pressure, $x$ is the axial coordinate, $k$ is the wave number, $c$ is the velocity of wave propagation, ${\rho }_0$ is the density of the medium, $A$ and $B$ are coefficients and $u$ stands for particle velocity. When using Eqs. (1), (2), the transfer matrix of a uniform tube can be written as:

where $v$ is the mass velocity, $Y$ is the corresponding characteristic impedance. The transfer matrix for the $r$th element can be denoted by $\left[T_r\right]$. {$p_r$, $v_r$} is called the state vector at the upstream point $r$, and {$p_{r-1}$, $v_{r-1}$} is called the state vector at the downstream point $r-1$.

For types of extended-tube resonators, the equivalent impedance $Z_r$ at the junction is given by Eq. (3), that is [2]:

where ${\varsigma }_{end}$ is the normal impedance.

Therefore [2]:

Further, transfer matrix of a lumped element can be written as [2]:

2.2. Experimental validation

In order to validate whether this method is applicable to hydraulic systems, Eqs. (3) and (6) were used to simulate a hydraulic suppressor for a simple expansion chamber (SEC) and a double-tuned extended-tube chamber (DTETC), which are shown in Figs. 1, 2. Moreover, here $t$stands for wall thickness.

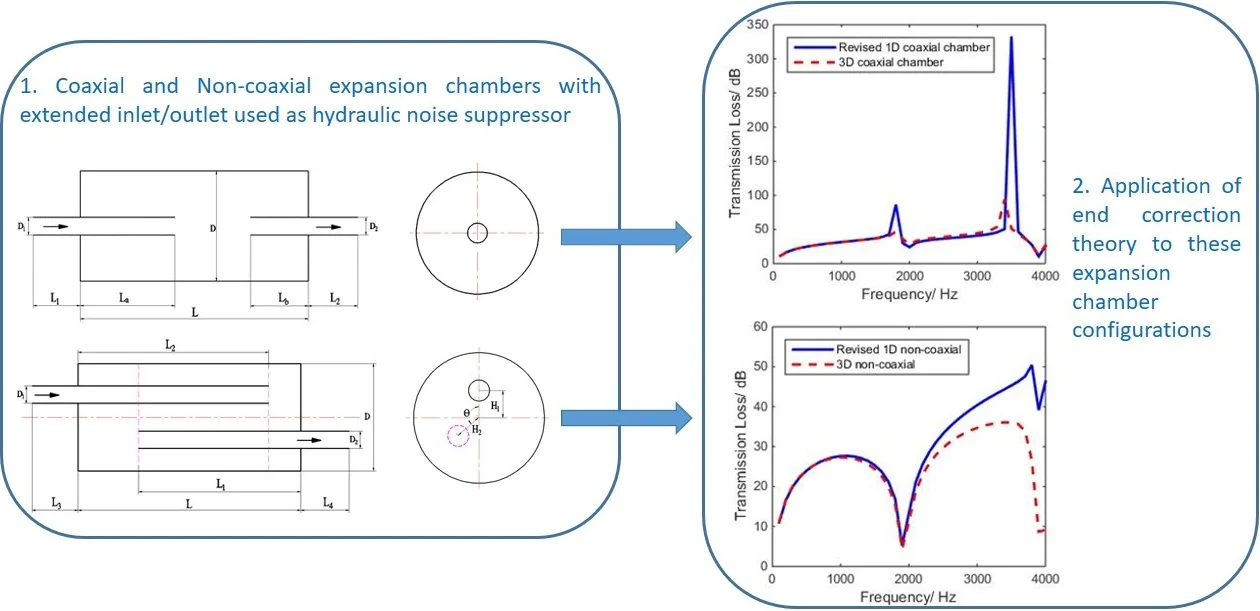
Fig. 1Scheme of simple expansion chamber (SEC) hydraulic suppressor: L= 175 mm, D1=D2= 38.6 mm, D= 68 mm, t= 2 mm, L1=L2= 74 mm

a) Elevation view

b) Left view

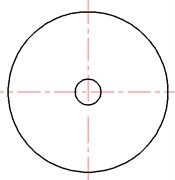
Fig. 2Scheme of double-tuned extended-tube chamber (DTETC) hydraulic suppressor: L= 175 mm, La=L/2, Lb=L/4, D1=D2= 38.6 mm, D= 68 mm, t= 2 mm, L1=L2= 74 mm

a) Elevation view

b) Left view

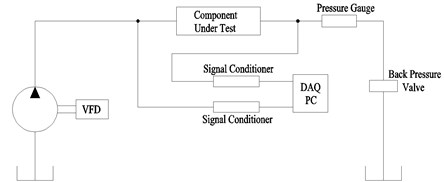
A scheme of the test rig can be seen in Fig. (3). Flow is provided to the system from a 9 piston axial piston pump driven by a variable frequency drive (VFD). The data from each pressure sensor are collected by a data acquisition card mounted inside of a PC.

Fig. 3Scheme of test setup for measurement of pressure pulsation of hydraulic suppressor

The hydraulic suppressors and their components are shown in Fig. 4.

The cut-off frequency, $f_{cut-off}$, of Figs. 1, 2 is given by [2]:

where $D$ is the tube diameter.

Fig. 4Experimental devices of SEC and DTETC: 1 – union joints, 2 – pressure sensors, 3 – inserted tubes, 4 – expansion chamber cavity

a)

b)

Considering the limitation of experimental installations, the frequency band is defined as 2000 Hz. The given configurations have been validated below.

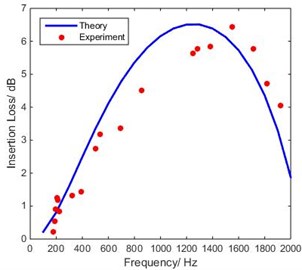
Figs. 5, 6 show the experimental validation for SEC and DTETC hydraulic suppressors. It is clear that predictions of the 1D analytical approach presented here compare well with those observed experimentally.

Fig. 5Comparison of theoretical IL of SEC with experimental measurements

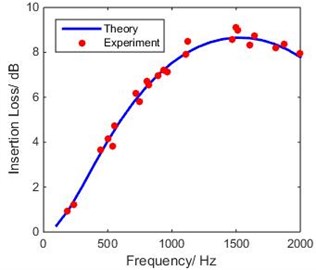
Fig. 6Comparison of theoretical IL of DTETC with experimental measurements

4.1. Study on end corrections of coaxial expansion chamber hydraulic suppressor

The geometry shall be modeled as shown in Fig. 7.

The cut-off frequency of Fig. 7 is given by:

Considering this cut-off frequency, the research spectrum is defined as 4000 Hz. Predictions of the 1-D model were compared with those of the 3-D model, as shown in Fig. 8.

Fig. 7Coaxial expansion chamber hydraulic suppressor with extended inlet and outlet: D= 0.2 m, D1=D2= 0.03 m, L= 0.36 m, La= 0.18 m, Lb= 0.09 m, L1=L2= 0.07 m

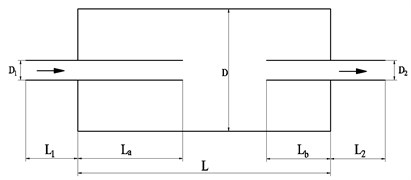
a) Elevation view

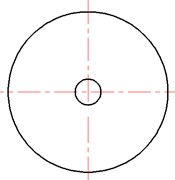
b) Left view

Fig. 8Comparison between 1-D and 3-D models of coaxial expansion chamber

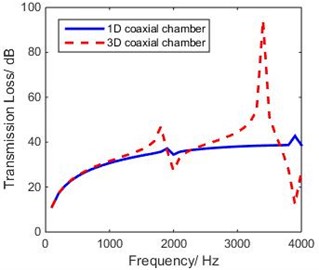
The Fig. 8 shows that the two peaks of the 3-D curve shift to the left of those of 1-D curve, which is similar to the results of corresponding mufflers. Hence, in reference to the acoustic length corrections of expansion chamber mufflers, the resonance peaks would occur at [2]:

where the effective length $L_{\mathrm{e}\mathrm{f}\mathrm{f}}$:

Therefore, the end correction is given by [10]:

where $f_r$ is the first resonance frequency evaluated by FEM, $L_g$ is the geometrical length of the inserted tube.

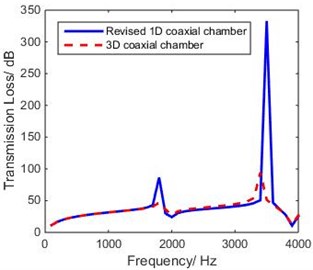
Fig. 9 shows that the resonance frequencies due to extended inlet/outlet are observed to occur at 1800 Hz and 3500 Hz. Using Eq. (12), the end corrections are calculated as 14.4 mm and 10 mm respectively. Predictions of the 1-D model match with those of the 3-D model only when we added the end corrections to the geometric length for use in the 1-D model [10], as shown in Fig. 10.

Fig. 10 shows that the first two peaks of the 1-D curve are in good agreement with those of FEM analysis; that means that the theory of end corrections is applicable to coaxial expansion chamber hydraulic suppressors.

Fig. 9Theoretical TL of extended inlet and outlet of coaxial expansion chamber

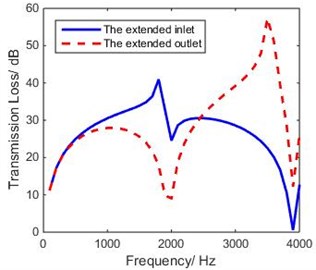
Fig. 10Comparison of theoretical TL of revised 1-D and 3-D model of coaxial expansion chamber

4.2. Study on end corrections of non-coaxial expansion chamber hydraulic suppressor

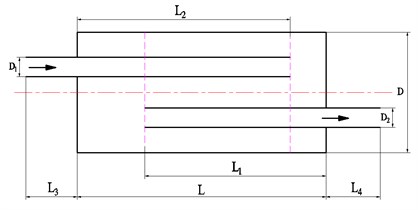
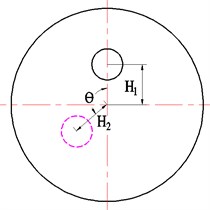
The theory similar to the one from 4.1 is used to study whether the end correction theory is applicable to non-coaxial expansion chamber hydraulic suppressors. The geometry need to be modeled as shown in Fig. 11.

Fig. 11Non-coaxial expansion chamber hydraulic suppressor with extended inlet and outlet: D= 0.2 m, D1=D2= 0.03 m, L= 0.36 m, L1= 0.28 m, L2= 0.3 m, L3=L4= 0.07 m, H1=H2= 0.04 m, θ= 180°

a) Elevation view

b) Left view

Predictions of the 1-D model were compared with those of the 3-D model, as shown in Fig. 12.

Fig. 12 shows that the first peak in the 3-D model is in good agreement with the corresponding peak in the 1-D model. However, the second peak in the 3-D model moved to the right of the corresponding peak in the 1-D model. Therefore, in order to consider the evanescent 3-D effects near the discontinuities, the geometric length in the 1-D model has to be increased by end corrections to achieve the effective acoustic length [10], which is the same as in 4.1. By using the FEM again, the theoretical TL of the extended inlet/outlet was obtained, as shown in Fig. 13.

Fig. 13 shows that the resonance frequencies due to extended inlet/outlet are observed to occur at 1200 Hz and 1300 Hz. Using Eq. (12), the end corrections were calculated as –8.3 mm and –10.8 mm respectively. The results of revised the 1-D model, and those of 3-D model were compared with them, as shown in Fig. 14.

Fig. 14 shows that the second peak of the 1-D curve departs even farther from that of the FEM analysis; that means that the theory of end corrections is not applicable to non-coaxial expansion chamber hydraulic suppressors.

Fig. 12Comparison between 1-D and 3-D model of non-coaxial expansion chamber

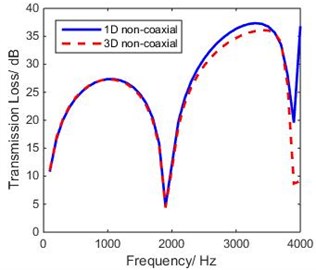
Fig. 13Theoretical TL of extended inlet and outlet of non-coaxial expansion chamber

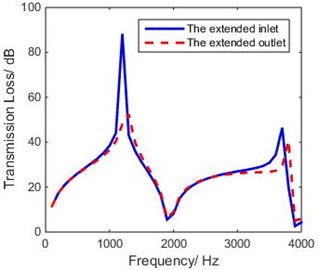
Fig. 14Comparison of theoretical TL of revised 1-D and 3-D model of non-coaxial expansion chamber