Degradation feature extraction method for piezoelectric ceramic of ultrasonic motor based on DCT-SV cross entropy

1. Introduction

For the advantages of high torque, quick response, no electromagnetic and auto-locking, ultrasonic motors have been widely used in the areas such as aerospace, medical equipment, optical instruments, robots, and new military equipment [1, 2]. Crack on piezoelectric ceramic is the main reason leading to failure of ultrasonic motors. It is necessary to pay considerable attention to the degradation feature extraction for piezoelectric ceramic, so that early warning and prevention could be made in time especially in the case of slight degradation.

The literature referring to the crack of piezoelectric ceramic mainly focuses on the mechanism and stress analysis [3-5]. In ultrasonic motor, monitor electrode voltage (MEV) is often used to monitor the vibration of stator. Since the MEV generated by the positive piezoelectric effect is similar to the signal generated by the acceleration sensor, the fault diagnosis methods based on vibration analysis have great reference value for this study. The basement of the feature extraction is the signal processing for obtaining sensitive failure information, and various methods have been applied in signal analysis and fault diagnosis recently, such as wavelet transform and empirical mode decomposition (EMD). Wang Z. [6] extracted the rolling bearing fault feature parameters by the best set of mother wavelets. Hu Q. [7] proposed an effective method for rotating machinery based on a weighted extreme learning machine with wavelet packet decomposition. Li Y. [8] applied bandwidth EMD and adaptive multi-scale morphology analysis for incipient fault diagnosis of rolling bearings. Yu X. [9] improved the accuracy of bearing fault diagnosis by local Fisher discriminant analysis and EMD based on vibration signals. However, these popular methods also have unsolved problems: One is the selection of thresholds and wavelet basis in wavelet transform; the other one is the mode fixing and end effect in EMD method.

In the past few years, signal processing methods based on spectral information analysis are widely used in fault diagnosis of mechanical devices. Among them, local mean decomposition as a novel time–frequency analysis method, can self-adaptively decompose a complicated signal into a set of components, each of which is the product of an envelope signal and a purely frequency modulated signal. Zhao H. [10] proposed a compound interpolation envelope local mean decomposition for fault diagnosis of reciprocating compressor, the envelope frequency spectrum presented a more significant peak of fault frequency. Li D. [11] proposed an enhanced bispectrum technique for incipient induction motor fault detection, and the effectiveness of the method was examined by different operating conditions. Hassan M. A. [12] introduced a new concept based on the bicoherence spectrum to assess the health conditions of helicopter drive train. Discrete Cosine Transform (DCT) as the spread of Fourier transform, has the property of energy aggregation [13, 14]. Wang Y. [15] proposed an improved DCT de-noising method for vibration signal to reveal the performance degradation of the hydraulic pump. Furthermore, singular value decomposition (SVD) is also widely used in the rotating machinery fault diagnosis. Kang M. [16] proposed SVD-based feature extraction to categorize the faults of the induction motor by support vector machine. Yang Q. [17] introduced an efficient solution to diagnose multiple mechanical faults in wind turbine gearbox by EMD and SVD joint approach. Yang H. [18] presented sliding window de-nosing K-SVD method for bearing fault diagnosis. Liu Y. [19] assembled SVD with wavelet transformation to extract the fault feature for submersible pump.

Entropy is able to quantify the disorder or uncertainty of probability distribution, and it has been widely applied in damage monitoring. Zhao H. [20] proposed a novel hermite local mean decomposition to construct the envelopes, and the multiscale fuzzy entropy was successfully used for bearing clearance fault diagnosis of reciprocating compressor. Ai Y. T. [21] fused singular spectrum entropy, power spectrum entropy, wavelet space spectrum entropy and wavelet energy spectrum entropy for the rolling bearing fault diagnosis. Cross entropy is an index that can reflect the deviation degree of two sets of probability distribution. The smaller cross entropy value, the more consistent the probability distribution, and vice versa. Ye J. [22] used cross entropy to diagnosis the main fault types of turbine, which is a good reference for degradation feature extraction of ultrasonic motor.

As far as degradation feature extraction for piezoelectric ceramic is concerned, the energy transmission would be subjected to a disturbance as the traveling wave passes through the crack on ceramic. MEV can reflect the vibration of piezoelectric ceramic in ultrasonic motor [23]. For the reason that DCT has the property of energy aggregation, DCT coefficients of MEV signal will be sensitive to energy change caused by the crack. The DCT coefficients can be used for information extraction to improve the correlation with the degradation. However, DCT just separates the useful information and noise in different frequency ranges, and the noise will still affect the results of degradation feature extraction based on information entropy analysis. In traditional method, the noise can be filtered out by removing the high frequency coefficients which are usually selected by engineering experience [15]. Therefore, the filtering results are largely influenced by human factors. Furthermore, drive frequency of the ultrasonic motor generally needs to be more than 20 kHz, the traditional method would also result in the loss of useful information. To solve above problems, singular value (SV) will be incorporated into the calculation of information entropy in this paper. A matrix can be constructed by DCT coefficients of MEV signal, then SV sequence of the matrix will be used to extract cross entropy for improving anti-noise performance.

Consequently, a novel degradation feature extraction method for piezoelectric ceramic in ultrasonic motor is proposed based on DCT-SV cross entropy. The remainder of this paper is organized as follows: In Section 2, the SV sequence based on DCT coefficients is given. Then the cross entropy quantifying the distribution differences between test sample and standard sample will be detailed. In Section 3, the effectiveness of the proposed method will be validated with experimental results. Finally, the conclusions are provided in Section 4.

2. DCT-SV cross entropy

The MEV signal sequence is noted as $x\left(n\right)$ with $N$ points, $n=$1, 2,…, $N$. The DCT coefficients can be defined as the following formula [24]:

where $k=$ 1, 2,…, $N$, $u\left(1\right)=\sqrt{1/N}$, $u\left(k\right)=\sqrt{2/N}$, $k\ne 1$.

DCT has the property of compacting the most energy within the fewest number of coefficients. In order to reduce the influence of human factors in traditional DCT de-noising method, SV is incorporated into the calculation of information entropy. The proposed DCT-SV cross entropy can be described as follows.

Construct a matrix $A$ according to DCT coefficient sequence $y\left(k\right)$:

where $m\ge$1, $n\ge$ 1 and $n$ is the integration of $N/m$.

SVD of matrix $A$ can be expressed as follows [25]:

where $P$ and $Q$ are orthogonal matrixes, $D=diag({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_L)$, $L$ is the order of $A$.

The weight coefficient of singular value can be defined as:

where $i=$1, 2,…, $L$.

The DCT-SV cross entropy which is taken as the degradation feature, is defined as follows:

where ${\mu }_t=\left\{{\mu }_{ti}|i=1,\dots ,L\right\}$ denotes the weight coefficient distribution of test data, ${\mu }_s=\left\{{\mu }_{si}|i=1,\dots ,L\right\}$ denotes the one of standard data in normal state.

Therefore, the proposed DCT-SV cross entropy can quantify the distribution difference between test data and standard data. The smaller the DCT-SV cross entropy, the closer the standard data and test data are. Furthermore, $E_c=$0 if and only if ${\mu }_s={\mu }_t$.

The flowchart of degradation feature extraction is concluded as Fig. 1.

3. Experimental results

3.1. Data sampling of MEV signal

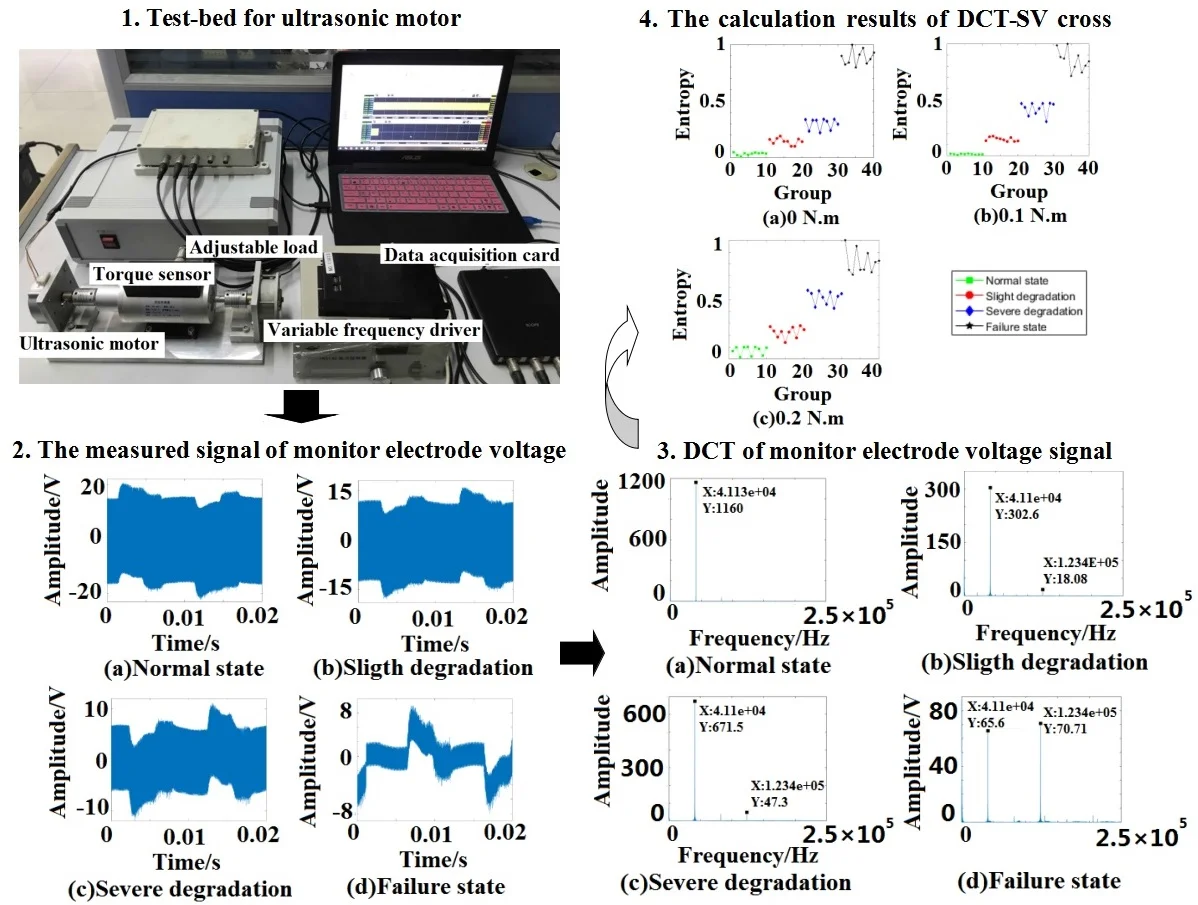
The data sampling of MEV signal was carried out by the ultrasonic motor test-bed, which is shown in Fig. 2.

Fig. 1The flowchart of degradation feature extraction

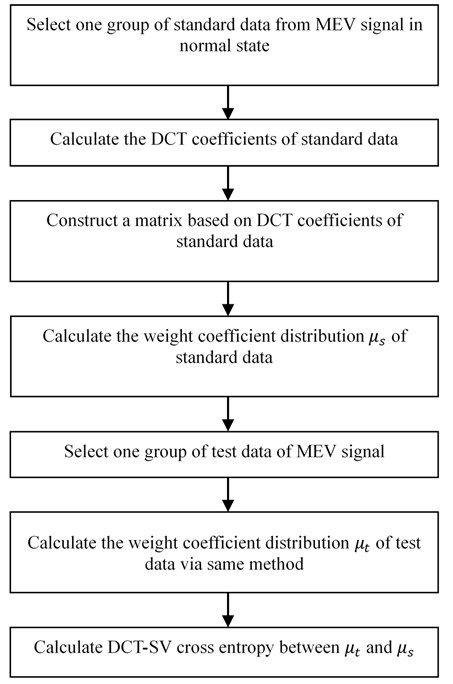
Fig. 2Test-bed for ultrasonic motor

The tested ultrasonic motor is a TRUM-60-P. Its maximum torque is 0.6 N·m. The speed is controlled by a variable frequency driver, and the load can be changed by a magnetic powder brake. The frequency of MEV was 41 kHz, and the signal was collected by the Handyscope HS4 data acquisition card of TiePie engineering. The sampling frequency was set to be 500 kHz, and the sampling time of each group data was 2 s. The MEV signals were recorded in three load conditions including 0 N·m, 0.1 N·m and 0.2 N·m. There were 40 test samples under each load condition, and 10 test samples in each degradation state. The test samples were numbered as follows: 0-10 groups were actual normal state, 11-20 groups were actual slight degradation, 21-30 groups were actual severe degradation, and 31-40 groups were actual failure state.

The piezoelectric ceramics of four degradation states are shown in Fig. 3.

Fig. 3The piezoelectric ceramics in four degradation states

a) Normal state

b) Slight degradation

c) Severe degradation

d) Failure state

e) Crack details in slight case

f) Crack details in severe case

g) Crack details in failure case

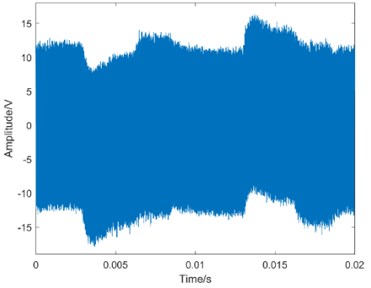
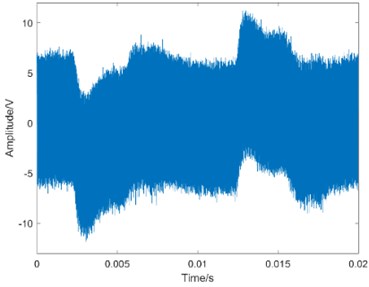
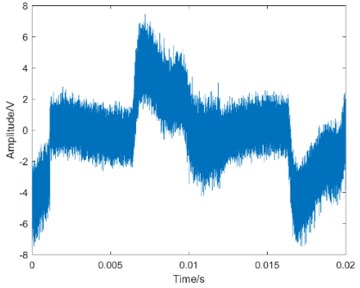
Fig. 4The waveform of MEV

a) Normal state

b) Slight degradation

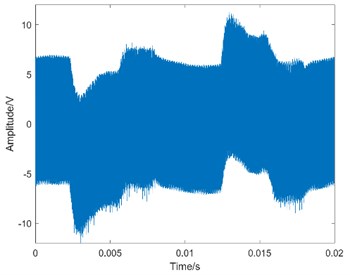
c) Severe degradation

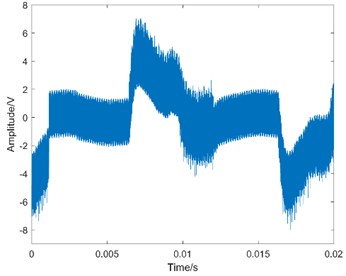
d) Failure state

The surface conditions of the cracks are described as follows:

(1) Normal state: intact;

(2) Slight degradation: the average width of crack is 0.2 mm and the length is 7.6 mm;

(3) Severe degradation: the average width of crack is 0.7 mm and the length is 8.7 mm;

(4) Failure state: the average width of central crack is 0.4 mm and the length is 2.3 mm. In addition, there are defect (12.2 mm²) and pitting corrosion (4.1 mm²) located on both sides of the crack, respectively.

Taking operation condition 0 N·m as an example, the waveform of MEV is shown in Fig. 4.

3.2. DCT spectrum

Taking the no-load condition as an example, the DCT spectrum in four degradation states is shown as Fig. 5.

From the comparison of four sub-graphs in Fig. 5, the 41.1 kHz driving component can be clearly distinguished. With the degradation development and the attenuation of stator vibration, the amplitude of the driving component is gradually decreasing. On the contrary, it is also worth noting that there are some components increasing with the degradation development. Taking the 123.4 kHz component as an example, it is almost close to zero in normal state, the amplitude in severe degradation state is slightly larger than that in slight degradation state, and the amplitude increases significantly in failure state. Based on the above analysis, it is true that the DCT coefficients contain some useful information varying regularly with the degradation. Furthermore, DCT spectrum becomes more complex from normal state to failure state. Therefore, the entropy representing DCT coefficient complexity can be used for the degradation feature extraction.

Fig. 5The DCT spectrum of MEV signal

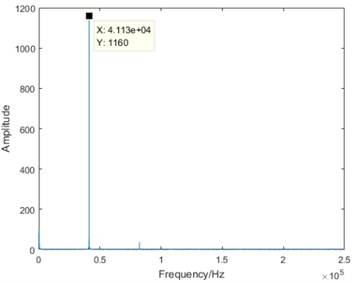
a) Normal state

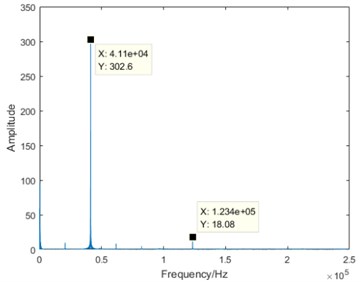
b) Slight degradation

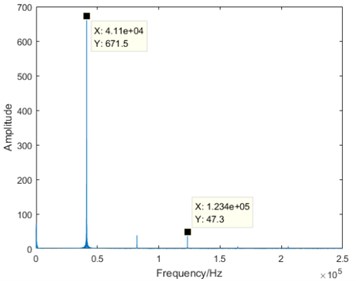
c) Severe degradation

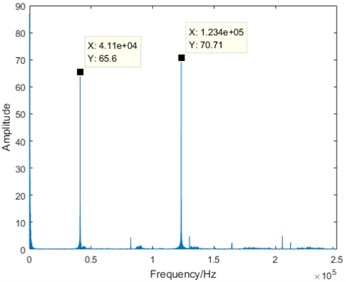
d) Failure state

3.3. DCT entropy

In order to verify the superiority of the proposed DCT-SV cross entropy, DCT entropy was used for comparative analysis. The DCT entropy is described as follows [26]:

6

$E_{DCT}=-\sum _{k=1}^{n}y\left(k\right)\mathrm{l}\mathrm{n}\left(y\left(k\right)\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}k=\mathrm{1,2},\dots ,N,$

where $y\left(k\right)$ is the DCT coefficients of MEV. $N$ is the data length of test sample.

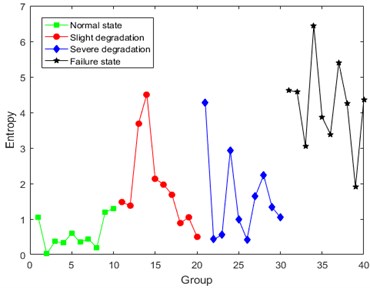
Taking operation condition 0 N·m as an example, the results of DCT entropy in four degradation states are shown as Fig. 6.

Fig. 6Results of DCT entropy

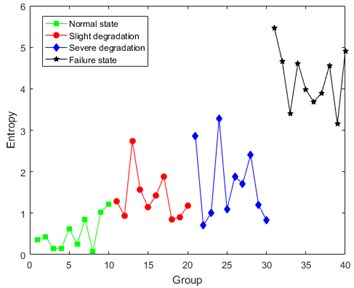
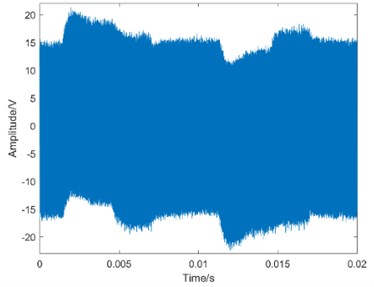
Fig. 7Waveform of the simulated signal with 10 dB noise

a) Normal state

b) Slight degradation

c) Severe degradation

d) Failure state

Analysis of Fig. 6 shows that the values of DCT entropy are generally increasing with the constant development of degradation, which represents that the DCT coefficients of MEV signal contains degradation information caused by the crack. However, the first three degradation states can’t be distinguished very clearly. The volatility of DCT entropy in the same degradation state is still relatively large. The main reason for this situation is considered to be the noise interference in MEV signal.

To further verify the noise influence on the calculation results, the simulated 10 dB noise was added to the measured signal, and the corresponding waveform is shown in Fig. 7.

The DCT entropy results of the simulated signal are shown in Fig. 8.

Compared with Fig. 6, the volatility in Fig. 8 becomes larger, and the difference between failure state and the first three states gets smaller. Consequently, it is unreasonable to take DCT entropy as the degradation feature, and the noise influence on the results of DCT entropy has been verified again.

The traditional way filtering out the noise is to remove the high frequency DCT coefficients according to engineering experience which is largely influenced by human factors. In this paper, DCT-SV cross entropy will be taken as the degradation feature to improve the anti-noise performance.

Fig. 8DCT entropy results of the simulated signal

3.4. Degradation feature extraction based on DCT-SV cross entropy

3.4.1. The parameter selection of the constructed matrix

The row number $m$ in the constructed matrix determines the length of SV sequence, and SV is proportional to the amount of information [27]. According to Eq. (5), $m$ will affect the calculation results of DCT-SV cross entropy. Consequently, the choice of $m$ value will be discussed in the following. Limited by the paper space, the SV sequences of constructed matrices in which $m$ ranges from 1 to 10, are listed in Table 1.

Table 1The statistics of SV sequence

	${\sigma }_1$	${\sigma }_2$	${\sigma }_3$	${\sigma }_4$	${\sigma }_5$	${\sigma }_6$	${\sigma }_7$	${\sigma }_8$	${\sigma }_9$	${\sigma }_{10}$
$m=$1	90.504
$m=$2	81.760	38.811
$m=$3	84.815	29.946	10.032
$m=$ 4	74.023	50.203	12.827	5.171
$m=$5	86.169	23.586	10.834	9.190	2.781
$m=$ 6	86.219	22.220	12.741	5.812	3.036	2.127
$m=$7	86.902	20.299	12.886	5.584	4.185	2.696	2.047
$m=$ 8	85.140	19.265	12.924	4.710	3.284	1.967	1.802	1.686
$m=$ 9	86.763	20.483	12.627	5.399	3.498	2.383	1.991	1.578	0.680
$m=$ 10	86.557	20.019	13.602	5.169	3.253	2.101	1.718	1.503	0.673	0.522

Based on the row information summarized in Table 1, it is clear that SV decreases gradually with the increasing of column number, and it means that the information corresponding to SV also decreases gradually.

According to Eq. (4), the weight coefficient of SV is defined to reflect the information proportion. The statistics of weight coefficient are shown in Table 2.

In this paper, we set 0.01 as the threshold for the choice of $m$ value. The SV whose weight coefficient is less than 0.01 (1 %) will be considered to be meaningless, because the corresponding information is small enough to be ignored. From the statistics in Table 2, we can notice that, as the column number reaches up to 9, the weight coefficients highlighted in bold will be less than the threshold value 0.01. Therefore, $m=$8 was selected to construct a matrix for DCT-SV cross entropy.

Table 2The weight coefficients statistics for SV

	${\mu }_1$	${\mu }_2$	${\mu }_3$	${\mu }_4$	${\mu }_5$	${\mu }_6$	${\mu }_7$	${\mu }_8$	${\mu }_9$	${\mu }_{10}$
$m=$ 1	1
$m=$ 2	0.678	0.322
$m=$ 3	0.680	0.240	0.080
$m=$ 4	0.520	0.353	0.090	0.036
$m=$ 5	0.650	0.178	0.082	0.069	0.021
$m=$ 6	0.652	0.168	0.096	0.044	0.023	0.016
$m=$ 7	0.646	0.151	0.096	0.041	0.031	0.020	0.015
$m=$ 8	0.651	0.147	0.099	0.036	0.025	0.016	0.014	0.013
$m=$ 9	0.641	0.151	0.093	0.040	0.026	0.018	0.015	0.012	0.005
$m=$ 10	0.641	0.148	0.101	0.038	0.024	0.016	0.013	0.011	0.005	0.004

3.4.2. Results of DCT-SV cross entropy

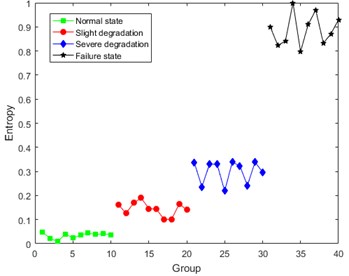
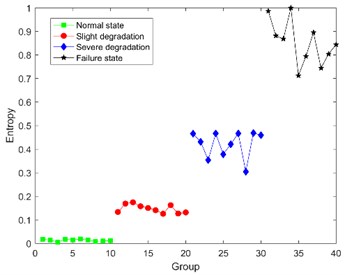
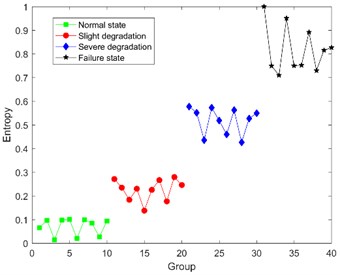
Under the condition that $m=$8, the DCT-SV cross entropy results of test sample in three load conditions are shown in Fig. 9.

Fig. 9 shows that DCT-SV cross entropy keep a clear uptrend with the degradation in all three load conditions, and there are also clear discrimination from normal state to failure state. Furthermore, it also has a good performance to discover slight degradation.

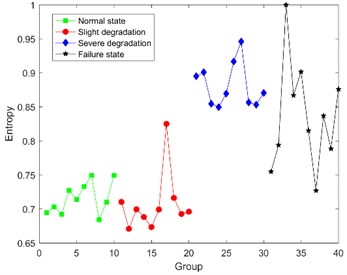
For further analysis, Bispectral analysis is adopted to extract the degradation feature for the following comparison. The calculation results of Bispectral singular entropy are shown in Fig. 10 [28].

Table 3Comparison between DCT-SV cross entropy and Bispectral singular entropy

Feature extraction method	Normal state	Slight degradation	Severe degradation	Failure state
DCT-SV cross entropy (0 N·m)	0.052±0.005	0.145±0.044	0.279±0.060	0.898±0.101
DCT-SV cross entropy (0.1 N·m)	0.012±0.006	0.150±0.024	0.386±0.082	0.856±0.144
DCT-SV cross entropy (0.2 N·m)	0.057±0.043	0.209±0.071	0.502±0.076	0.855±0.145
Bispectral singular entropy (0 N·m)	0.721±0.029	0.748±0.077	0.896±0.050	0.864±0.137
Bispectral singular entropy (0.1 N·m)	0.719±0.027	0.679±0.031	0.888±0.089	0.843±0.157
Bispectral singular entropy (0.2 N·m)	0.802±0.022	0.732±0.069	0.884±0.045	0.875±0.125

Fig. 9The calculation results of DCT-SV cross entropy

a) 0 N·m

b) 0.1 N·m

c) 0.2 N·m

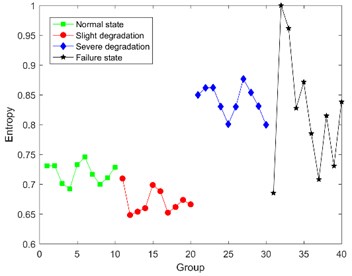
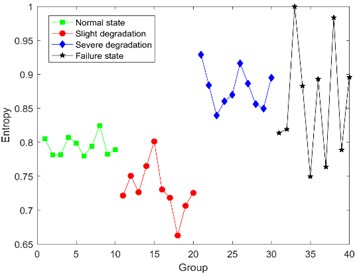
Fig. 10The results of Bispectral singular entropy

a) 0 N·m

b) 0.1 N·m

c) 0.2 N·m

Fig. 10 shows that it seems reasonable that the Bispectral singular entropy values of the latter two states are slightly higher than that of the former two states. But there is a wrong logic that the average entropy value of normal state is higher than the one of slight degradation, and the values in severe degradation and failure state are overlapped and indistinguishable. Consequently, Bispectral singular entropy can’t be used as the feature to indicate different degradation state for ultrasonic motor.

In order to verify the superiority of the proposed method, comparison between DCT-SV cross entropy and Bispectral singular entropy are listed in Table 3.

From Table 3, it is obvious that not only DCT-SV cross entropy keeps better correlation with degradation, but also the fluctuation range of DCT-SV cross-entropy is smaller than that for Bispectral singular entropy.

3.5. Anti-noise performance of degradation feature

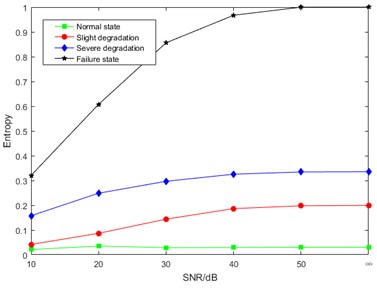
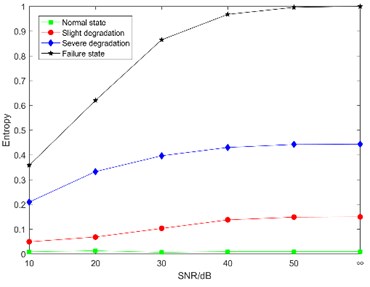
In order to verify the anti-noise performance of the proposed DCT-SV cross entropy, a numerical simulated noise was added to the measured MEV signal. There were five kinds of signal-to-noise ratio including 10 dB, 20 dB, 30 dB, 40 dB, 50 dB, and the one of the original measured signal was marked as “∞”. The DCT-SV cross entropy results with simulated noise are shown in Fig. 11.

The analysis of Fig. 11 shows that DCT-SV cross entropy values of the four degradation states get closer with the increasing noise intensity. The main reason for this situation is that, to some extent, the noise cancels out the complexity difference of DCT coefficients among the states. However, benefiting from the anti-noise ability of SVD, the proposed feature still keeps a good performance to follow the degradation trend from normal state to failure state [29].

Fig. 11DCT-SV cross entropy of the signal with simulated noise

a) 0 N·m

b) 0.1 N·m

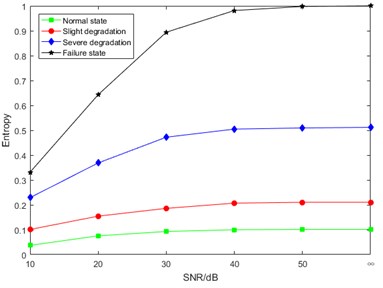
c) 0.2 N·m

4. Conclusions

A degradation feature extraction method for piezoelectric ceramic of ultrasonic motor was proposed based on DCT-SV cross entropy, which was verified by experiment results analysis. The conclusions can be drawn as follows:

1) DCT coefficients of MEV signal can sensitively reflect the energy change in stator vibration of ultrasonic motor, and the coefficients can be used to extract the degradation feature for piezoelectric ceramic.

2) DCT-SV cross entropy as the degradation feature, is sensitive to the piezoelectric ceramic degradation state changing, and has a good performance to discover early degradation. It is meaningful for the condition-based maintenance of ultrasonic motors.

3) DCT-SV cross entropy presents a satisfactory anti-noise performance which has been verified by the simulated noise.