A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance

Nguyen, Vanliem; Zhang, Jianrun

doi:10.21595/jve.2020.20966

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2020

Check for updates

A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance

Vanliem Nguyen¹

Jianrun Zhang²

¹School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi, 435003, China

^{1, 2}School of Mechanical Engineering, Southeast University, Nanjing, 211189, China

Corresponding Author:

Jianrun Zhang

Cite the article Download PDF

Downloads 1319

WoS Core Citations 4

CrossRef Citations 6

Abstract

In order to research the impact of the vibration on working stability of the vibration compaction system (VCS) and increase the paver’s performance, the acceleration responses at the screed surface under the excitation frequencies of the tampers and vibration screed are analyzed via the root mean square acceleration responses (RMSAR) at the bottom of the screed surface. A non-linear dynamic model of the VCS is then established to research the impact of the VCS’s dynamic parameters on the performance of paver via the objective functions of the vertical, pitch and roll RMSAR of the vibration screed. The dynamic parameters are then optimized based on a multi-objective genetic algorithm to enhance the paver’s performance. The experiment and simulation results show that the dynamic parameters greatly affect the paver’s performance. The compression performance is quickly increased, while the working stability and paving quality are reduced with increasing the angular deviations of tampers and excitation frequencies of both the tampers and vibration screed and vice versa. Also, the paver’s performance is significantly improved by using the optimal parameters of the VCS.

A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance

1. Introduction

To pave the asphalt mixture on the various pavements road uniformly and rapidly, the vibration compaction system (VCS) of the asphalt paver equipped with a couple of tampers and vibration screed had been applied [1-5]. The tampers were employed to squeeze the mixture of the asphalt which was paved on the surface of pavements to become tighter, while the vibration screed was employed to enhance smoothness and finish the pavements. Three performance indices of the compression efficiency, paving quality and working stability were then used to evaluate the performance of the asphalt paver [1, 6].

The existed researches showed that the compression performance of the asphalt paver was greatly influenced by both the compacting forces generated by the tampers and asphalt material’s properties [2, 7-11]. The research results of the effect of the temperature [12, 13] and plastic deformation [8, 14] of the hot mix asphalt materials on the paver’s performance indicated that the asphalt density and compression efficiency significantly depended on the hot mix asphalt. To reach the desired value of density, the fuzzy clustering techniques were applied to quickly analyze the compaction data of the hot mix asphalt [7]. Based on the compaction monitoring system [15], the errors in the compaction process including the compaction delay, unequal compaction converge and temperature of the mixed asphalt were then controlled. However, the temperature deviation on the paving surface was still high, thus, an infrared temperature scanning bar system [16] was also investigated and applied to solve this issue. The above research results show that compression efficiency was significantly ameliorated via the application of modern technology to control the characteristics of the asphalt mixture and compacting forces of the tampers. However, the above studies only focused on analyzing the effect of asphalt material properties on compression efficiency. Therefore, the compacting force was only considered under the excitation frequency of tampers, while the compacting force was depended not only by the mass and excitation frequency but also by the angular deviations of tampers [1, 2, 6]. Consequently, the impact of angular deviations of tampers characterized by the design parameters of the VCS on compression efficiency should be considered to fully evaluate the paver’s performance.

The influence of the design parameters of the VCS on the working stability and paving quality of the asphalt paver was then evaluated [1, 5, 6, 17]. Besides, the effect of the operating parameters of the VCS such as the moving speed, excitation frequencies, and mass of tampers on the pavement smoothness was also studied based on the acceleration response at the bottom of the vibration screed surface [18, 19]. The results showed that the vibration excitation of tampers significantly affected paving quality. Thus, a 2D model of the VCS was established to analyze the impact of excitation frequency of the tampers ( $f_{1}$ ) and vibrator screed ( $f_{2}$ ) on the accelerations and displacements of the front and rear screed [5]. The results showed that the vibration screed gained better service performance when the vibration frequency of $f_{1}$ was in a range of 10-20 Hz and $f_{2}$ was a range of 30-40 Hz. To enhance the working stability and paving quality, an excitation frequency range of both $f_{1}$ and $f_{2}$ from 0 to 45 Hz were optimized under the different pavements of the asphalt mixtures of SMA-13, AC-20, and AC-25 [2-4, 6]. The paving performance was then found at the excitation frequencies of $f_{1} =$ 15 Hz and of $f_{2} =$ 32 Hz [6]. All the above studies indicated that the performance of the asphalt paver was improved based on the optimization of the genetic algorithm. However, both the working stability and paving quality were still low under the optimal frequencies of $f_{1}$ and $f_{2}$ . In order to solve this issue, the eccentric distance of the eccentric shaft and mass of tampers were also optimized [20]. Based on the optimal results, the vibration amplitude at all nodes on the vibration screed was significantly decreased, thus, the surface quality of paving was also improved. In all the above studies, a 2D model was mostly used to analyze and optimize the parameters of the VCS. However, the actual width of the vibration screed is 9 or 12 m [5, 6], thus, the roll angle of vibration screed could significantly affected the working stability and paving quality. Conversely, this issue has not yet been concerned with the existed researches.

To fully reflect the impact of dynamic parameters of the VCS on the paver’s performance, the experimental study is given to analyze the actual performance of the asphalt paver. A non-linear dynamic model with three dimensions (3D) of the VCS is then established to research the impact of the dynamic parameters on the compression efficiency, paving quality and working stability of the asphalt paver. To improve the paver’s performance, multi-objective optimization of the genetic algorithm is then applied to optimize the dynamic parameters. The root mean square acceleration response (RMSAR) [5, 14] at the centre of gravity of vibration screed in all the vertical, pitch, and roll directions are chosen as the objectives to evaluate the compression efficiency ( $\bar{E}$ ), paving quality and working stability ( $\bar{Q}$ ). The innovation in the paper is that a 3D nonlinear dynamic model is given to fully evaluate the influence of the pitch and roll angles of the vibration screed on paving quality and working stability. All the dynamic parameters of the VCS are analyzed and optimized to improve the paver’s performance based on the experimental study and numerical simulation.

2. Experimental study and mathematical model

2.1. Experimental test

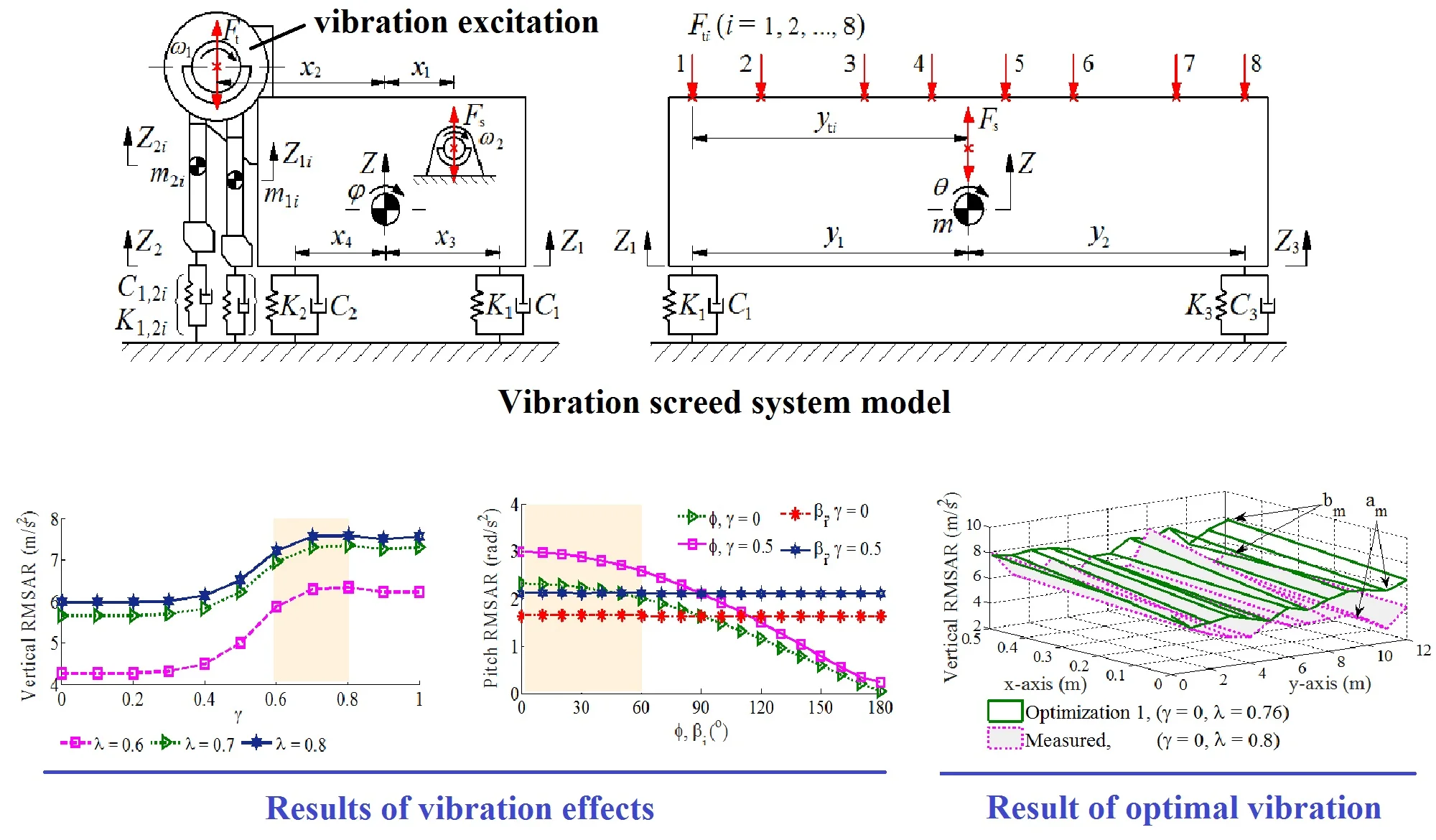
The dynamic parameters of the VCS including the excitation frequencies $f_{1}$ and $f_{2}$ of the tampers and vibrator screed, the angular deviations $α$ , $β_{i}$ , and $ϕ$ of excitation forces between the right and left sides of the first and second tampers, between tampers, and between the first and second tampers, as described in Fig. 5 and Eq. (10). In order to evaluate the vibration and stability of machines, the acceleration response calculated via the RMSAR was mainly applied [6, 11, 21]. This paper, the actual performance of the asphalt paver is analyzed based on the RMSAR of experimental results under the main excitations of $f_{1}$ and $f_{2}$ . The experimental process is performed as follows:

(i) Preparing instruments: An asphalt paver including a screed width of 12 m, a dynamic test, and analysis system of Belgium LMS, and 3D accelerometers ICP are given to determine the acceleration responses at the bottom of the screed surface. The sensors are calibrated and installed at 13 locations on the front $a_{m}$ and rear $b_{m}$ of the screed surface, ( $m =$ 0-12). The experimental model is illustrated in Fig. 1.

(ii) Experimental process: To measure the acceleration response on the screed surface, multi-point measurements of the vertical acceleration responses [11] at the bottom of the screed surface are used. The measurement process is performed in two cases: (1) under excitation frequency of tampers $f_{1} =$ {20 %, 40 %, 60 %, 80 %} of $f_{1 m a x}$ and without the excitation of the vibrator screed, $f_{2} =$ 0; (2) also under same vibration excitation of $f_{1}$ and using $f_{2} =$ 50 % of $f_{2 m a x}$ of the vibrator screed. However, it is difficult to accurately determine the input excitation frequencies of $f_{1}$ and $f_{2}$ , thus, based on the maximum rotation angular velocity of tampers and vibrator screed ( $ω_{1 m a x}$ and $ω_{2 m a x}$ ), the rotation angular velocity of $ω_{1}$ and $ω_{2}$ of tampers and vibrator screed are given by the operator as the vibration excitations for the experimental process. To simplify the analysis of results, the vibration excitation of the tampers and vibrator screed are defined by ratios $λ$ and $γ$ as follows:

1

λ = \frac{ω_{1}}{ω_{1 m a x}} = \frac{f_{1}}{f_{1 m a x}},

2

γ = \frac{ω_{2}}{ω_{2 m a x}} = \frac{f_{2}}{f_{2 m a x}} .

Therefore, two experimental cases are rewritten by Eq. (1) $λ =$ {0.2, 0.4, 0.6, 0.8} with $γ =$ 0 and (2) with $γ =$ 0.5. The time of a test is 30 s.

(iii) Extracting data: Through the signal processor and displaying the results, as shown in Fig. 1(b), the measured data including the vertical acceleration responses and the RMSAR at measured positions on the screed surface are carried out.

Fig. 1Diagrammatic sketch of the experimental set-up for the asphalt paver

a) Vibration compaction system

b) Asphalt paver: 1 – accelerometer; 2 – signal processor and display the results

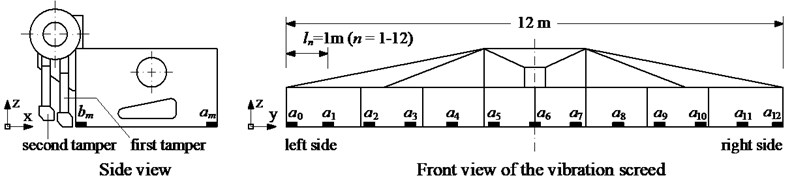
c) Installation locations of accelerometers on the vibration screed

2.2. Experimental result and analysis

In order to evaluate the paver’s performance, the indexes of the compression efficiency ( $\bar{E}$ ), paving quality and working stability ( $\bar{Q}$ ) are proposed based on statistical theory [22] as follows:

3

\bar{E} = \frac{\sum_{i = 1}^{n} X_{n}}{n},

4

\bar{Q} = \frac{\sum_{i = 2}^{n} |X_{n} - X_{n - 1}|}{n - 1},

where $X_{n}$ is the RMSAR at the measured points $n$ ; $\bar{E}$ is the average value of $X_{n}$ ; $\bar{Q}$ is the average deviation between the measured points of $X_{n}$ , $n = \{a_{m}, b_{m}\}$ ; thus, both the bigger value of $\bar{E}$ and the smaller value of $\bar{Q}$ meaning that the paver’s performance is better.

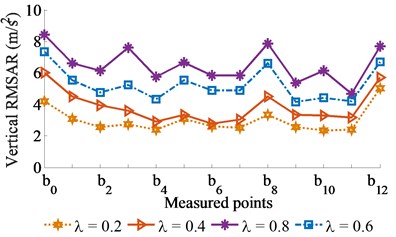
Fig. 2Experimental RMSAR results without excitation of vibrator screed (γ= 0)

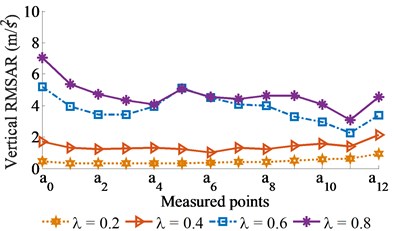
a) At front of screed surface

b) At rear of screed surface

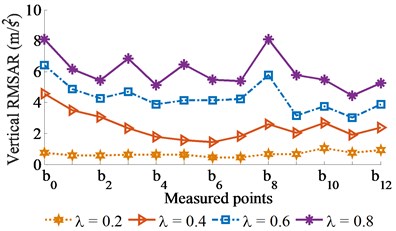
Fig. 3Experimental RMSAR results with excitation of vibrator screed γ= 0.5)

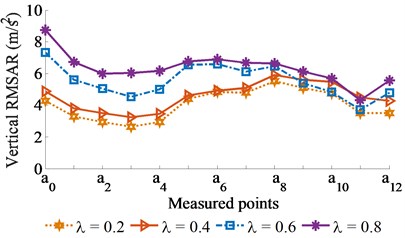
a) At front of screed surface

b) At rear of screed surface

The measured and statistical results of the vertical RMSAR at bottom of the screed surface under the various excitations of $λ =$ {0.2, 0.4, 0.6, 0.8} with $γ =$ 0 and 0.5 are shown in Figs. 2 and 3, and listed in Table 1. With $γ =$ 0 (without the excitation of $f_{2}$ ), observing the results in Fig. 2, it can see that the vertical RMSAR at the bottom of the screed surface is insignificantly skewed with $λ =$ 0.2 and 0.4. It implies that the pavement surface is relatively smooth but the compressive efficiency is low. When increasing excitation of $λ$ to 0.6 or 0.8, the vertical RMSAR at the bottom of the screed surface is strongly enhanced, thus, the compressive efficiency of the VCS is increased. However, the vertical RMSAR at the measured points at front/rear positions on screed surface are greatly skewed, these results show that the VCS works unstable and the paving quality is low, especially at $λ =$ 0.8. Consequently, the vibration excitation of $f_{1}$ greatly affects the paver’s performance. With $γ =$ 0.5 (adding 50 % of $f_{2}$ ), Fig. 3 shows that the vertical RMSAR is skewed not only greater but also higher their values without the $f_{2}$ . It is due to the effect of the $f_{2}$ part from the main excitation of $f_{1}$ . The calculated results in Table 1 also show that both the average values of $\bar{E}$ and $\bar{Q}$ are enhanced with increasing ratios of $λ$ and $γ$ . Thus, compressive efficiency is increased, while the paving quality and working stability are remarkably reduced.

In order to evaluate the impact of the vibration on the screed shaking which directly affects the smoothness and stability of the VCS, the vertical ( $Z)$ , pitch and roll ( $φ$ and $θ$ ) acceleration responses at the centre of gravity of the vibration screed can be calculated via the measured results of the vertical RMSAR at the front/rear points on the screed surface according to the kinetic relationship of screed. It is assumed that the effect of angle deformations of screed is negligible, thus, the acceleration responses of the vibration screed are calculated by [5, 11]:

5

\ddot{Z} = \frac{{\ddot{Z}}_{b_{6}} x_{3} + {\ddot{Z}}_{a_{6}} x_{4}}{x_{3} + x_{4}}, \ddot{φ} = \frac{{\ddot{Z}}_{b_{6}} - {\ddot{Z}}_{a_{6}}}{x_{3} + x_{4}}, \ddot{θ} = \frac{({\ddot{Z}}_{b_{1}} - {\ddot{Z}}_{b_{11}}) x_{3} + ({\ddot{Z}}_{a_{1}} - {\ddot{Z}}_{a_{11}}) x_{4}}{(l_{a_{1}} + l_{a_{2}}) (x_{3} + x_{4})},

where ${\ddot{Z}}_{k}$ is the vertical RMSAR at measured points, ( $k = a_{1}$ , $a_{6}$ , $a_{11}$ , $b_{1}$ , $b_{6}$ , $b_{11}$ ); $x_{3}$ , $x_{4}$ and $y_{a 1}$ , $y_{a 2}$ are the distances between the centre of gravity of the vibration screed and the corresponding measurement points in the directions of $x$ and $y$ .

Table 1The statistical results of the RMSAR on screed surface

$λ$	$γ =$ 0		$γ =$ 0.5
$λ$	${\bar{E}}_{1}$	${\bar{Q}}_{1}$	${\bar{E}}_{2}$	${\bar{Q}}_{2}$
$λ =$ 0.2	0.67	0.20	3.28	0.61
$λ =$ 0.4	1.91	0.45	4.11	0.57
$λ =$ 0.6	4.01	0.74	5.30	0.83
$λ =$ 0.8	5.23	0.93	6.32	0.93

Fig. 4Measured results of the RMSAR at the centre of gravity of the vibration screed

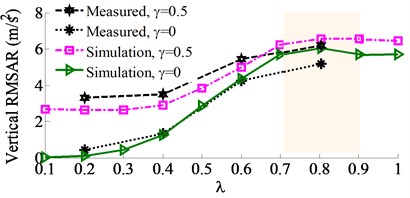
a) Vertical acceleration response

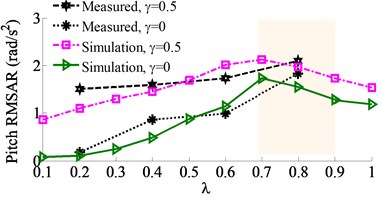
b) Pitch acceleration response

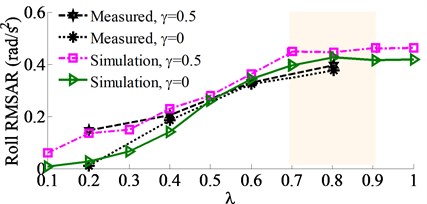
c) Roll acceleration response

Measured results of the RMSAR of the vibration screed under different excitations of $λ =$ {0.2, 0.4, 0.6, 0.8} with $γ =$ 0 and 0.5 are shown in Fig. 4. Observing Figs. 4(a)-(c), the results indicate that the RMSARvalues in all the vertical, pitch and roll directions are strongly changed by the ratios of $λ$ and $γ$ , particularly the $λ$ . Their values are slightly increased by $λ \leq$ 0.4, and strongly enhanced by $λ >$ 0.4. Besides, the RMSAR values with $γ =$ 0.5 are also higher than without $γ$ . This is due to the influence of increasing the vibration excitations of $f_{1}$ and $f_{2}$ . Thus, the compressive efficiency is significantly increased by increasing the ratios $λ$ and $γ$ , however, the paving quality and working stability are reduced due to increasing both the pitch and roll angles of the vibration screed, especially at $λ =$ 0.8. To fully reflect the influence of dynamic parameters on the paver’s performance, especially the screed shaking, the other dynamic parameters of the VCS such as the angular deviations $α$ , $β_{i}$ , and $ϕ$ of the tampers also need to be concerned. However, it is difficult to analyze the effect of these angular deviations on the paver performance based on the experimental method. To solve this problem, a 3D dynamic model of the VCS is then concerned.

2.3. Mathematical model of the VCS

In this study, a 3D dynamic model of the VCS which may fully assess the screed shaking on the paver’s performance is built to analyze the dynamic parameters of the VCS, as plotted in Fig. 5, where $Z$ , $φ$ , and $θ$ are the vertical, pitch and roll motions at the centre of gravity of screed; $m$ , $m_{1 i}$ , and $m_{2 i}$ are the mass of the screed, first and second tampers; $k_{1 i}$ , $k_{2 i}$ , $k_{j}$ and $c_{1 i}$ , $c_{2 i}$ , $c_{j}$ are the medium stiffness and damping coefficients of pavement at the bottom of the first/second tampers, and screed surface, respectively; $F_{t i}$ and $F_{s}$ are the vertical excitation forces produced by the rotating eccentric masses and excitation frequencies of the tampers and vibrator screed; $x_{j}$ and $y_{1,2}$ , $y_{t i}$ are the VSS’s longitudinal and lateral distances, $i =$ 1-8, $j =$ 1-4.

Fig. 5Vibration screed system model

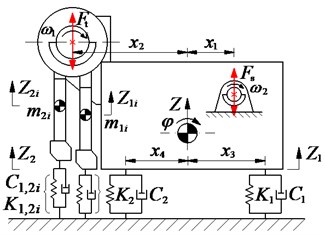
a) Side view

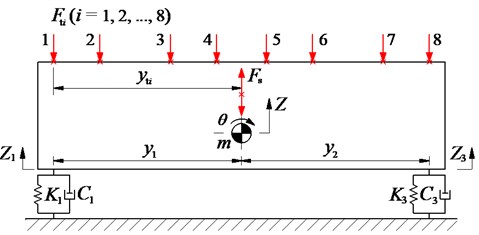
b) Front view

According to the nonlinear vibration theory and the VCS’s dynamic model, the motion equations are written by:

6

\begin{array}{l} m \ddot{Z} = F_{s} + \sum_{i = 1}^{8} F_{t i} - \sum_{j = 1}^{4} F_{j}, \\ I_{y} \ddot{φ} = \sum_{i = 1}^{8} F_{t i} x_{2} + \sum_{j = 1}^{4} (- 1)^{j + 1} F_{j} x_{u} - F_{s} x_{1}, \\ I_{x} \ddot{θ} = \sum_{j = 1}^{4} (- 1)^{v} F_{j} y_{v} + \sum_{i = 1}^{4} F_{t i} y_{t i} - \sum_{i = 4}^{8} F_{t i} y_{t i} . \end{array}

The vertical dynamic forces of the vibration screed-pavement interaction in the paving process is described by:

7

F_{j} = C_{j} {\dot{Z} + (- 1)^{j} x_{u} \dot{φ} + (- 1)^{v + 1} y_{v} \dot{θ}} + k_{j} {Z + (- 1)^{j} x_{u} φ + (- 1)^{v + 1} y_{v} θ\},

where $v =$ 1, $u = j + 2$ with $j =$ 1, 2; $v =$ 2, $u = j$ with $j =$ 3, 4.

With the mass $m_{s}$ and distance $e_{s}$ of the eccentric configuration of the vibrator screed, the excitation force of the vibrator screed is described as follows:

8

F_{s} = m_{s} e_{s} ω_{2}^{2} s i n ω_{2} t .

The excitation force of the first/second tampers affecting the vibration screed can be calculated by:

9

F_{t i} = \{\begin{array}{l} - m_{1 i} {\ddot{Z}}_{1 i} + C_{1 i} {\dot{Z}}_{1 i} + K_{1 i} Z_{1 i} \\ - m_{2 i} {\ddot{Z}}_{2 i} + C_{2 i} {\dot{Z}}_{2 i} + K_{2 i} Z_{2 i} \end{array}\}

10

\{\begin{array}{l} Z_{1 i} = e_{1 i} s i n (ω_{1} t + β_{i} + ζ α), \\ Z_{2 i} = e_{2 i} s i n (ω_{1} t + β_{i} + ζ α + ϕ), \end{array}

where $e_{1 i}$ and $e_{2 i}$ are the eccentric distances of tampers, $β_{i}$ is the angular deviations of excitation forces between tampers, $α$ is the angular deviation of excitation forces between the right and left sides of the first/second tampers, and $ϕ$ is the angular deviation of excitation forces between the first/second tampers.

By replacing Eq. (10) into (9) and the mathematical transformation, the $F_{t i}$ is rewritten by:

11

F_{t i} = m_{1 i} e_{1 i} ω_{1}^{2} s i n (ω_{1} t + β_{i} + ζ α) + m_{2 i} e_{2 i} ω_{1}^{2} s i n (ω_{1} t + β_{i} + ζ α + ϕ)

+ C_{1 i} e_{1 i} ω_{1} c o s (ω_{1} t + β_{i} + ζ α) + C_{2 i} e_{2 i} ω_{1} c o s (ω_{1} t + β_{i} + ζ α + ϕ)

+ K_{1 i} e_{1 i} s i n (ω_{1} t + β_{i} + ζ α) + K_{2 i} e_{2 i} s i n (ω_{1} t + β_{i} + ζ α + ϕ),

where $ζ =$ 0 with $i =$ 1-4, $ζ =$ 1 with $i =$ 5-8.

By combining Eqs. (6)-(8) and (11), all the acceleration responses of the vibration screed in the vertical, pitch and roll directions are solved, and the vertical acceleration responses at front/rear points ( $a_{m}$ and $b_{m}$ ) under the screed surface are thus calculated as:

12

{\ddot{Z}}_{ψ} = \ddot{Z} + (- 1)^{v} x_{v + 2} \ddot{φ} + (- 1)^{v + 1} y_{n} \ddot{θ},

where $ψ$ is $a_{m}$ or $b_{m}$ ; $v =$ 1 with $m =$ 0-6; $v =$ 2 with $m =$ 7-12.

In order to assess the effect of the dynamic parameters on the paver’s performance as well as compare the simulation results with test results, the RMSAR at points under the screed surface and at the centre of gravity of the vibration screed is calculated by [21, 23]:

13

R M S A R_{ψ} = \sqrt{\frac{1}{T} \int_{0}^{T} [{\ddot{Z}}_{ψ} (t)]^{2} d t},

14

R M S A R_{w} = \sqrt{\frac{1}{T} \int_{0}^{T} [a_{w} (t)]^{2} d t},

where $w$ is the symbol for $Z$ , $φ$ , or $θ$ ; ${\ddot{z}}_{ψ} (t)$ is the acceleration in the vertical direction at $a_{m}$ and $b_{m}$ calculated as in Eq. (12); $a_{w} (t)$ is the acceleration in the vertical direction of $w$ ; $T$ is the simulation time.

3. Simulation and discussion

To verify the accuracy of the mathematical model as well as analyze the impact of dynamic parameters on the paver’s performance, an excitation frequency range of tampers characterized by the ratios of $λ =$ {0.1, 0.2, …, 1.0} with two different excitations of the vibrator screed $γ =$ 0 and 0.5 are simulated and compared with the measured results under the same experimental condition. The lumped parameters of the VCS are listed as in Table 2.

Table 2Lumped parameters of the VCS

Parameter	Value	Parameter	Value
$m$ / kg	3083	$e_{s}$ / m	2.5×10^-3
$m_{11,18}$ / kg	78	$e_{i 1}$ / m	3×10^-3
$m_{12,17}$ / kg	110	$e_{i 2}$ / m	3×10^-3
$m_{13,16}$ / kg	70	$ω_{1 m a x}$ / rpm	1250
$m_{14,15}$ / kg	69	$ω_{2 m a x}$ / rpm	2700
$m_{21,28}$ / kg	80	$K_{1,3}$ / N m^-1	3.57×10⁶
$m_{22,27}$ / kg	114	$K_{2,4}$ / N m^-1	3.06×10⁶
$m_{23,26}$ / kg	71	$K_{i 1,2}$ / N m^-1	0
$m_{24,25}$ / kg	72	$C_{1,3}$ / Ns m^-1	58×10³
$x_{1}$ / m	0.114	$C_{2,4}$ / Ns m^-1	68×10³
$x_{2}$ / m	0.2	$C_{i 1,2}$ / Ns m^-1	0
$x_{3}$ / m	0.332	$β$ / ^o	90; 180
$x_{4}$ / m	0.163	$α$ / ^o	60
$y_{1}$ / m	6	$ϕ$ / ^o	{90; 120; 180}
$y_{2}$ / m	6	$i =$ 1-12

The comparison results of the RMSAR at the centre of gravity of the vibration screed are shown in the same Figs. 4(a)-(c). The results indicate that the characteristic curves of the RMSAR with the simulation are similar to the measured results. Therefore, the VCS’s model can be reliable to assess the simulation results.

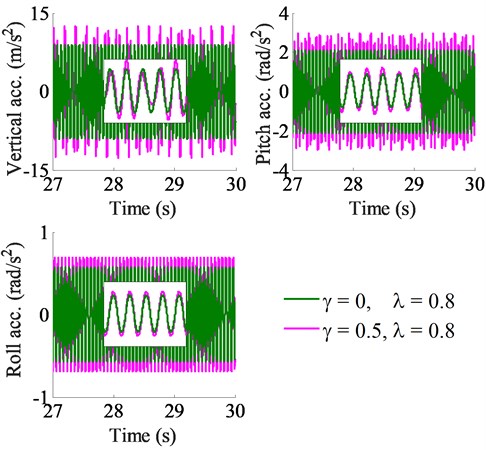
Fig. 6Acceleration responses of the vibration screed

3.1. Effect of the dynamic parameters

3.1.1. Effect of excitation frequency of tampers

The tempers are used to compact the asphalt pavement, thus, the excitation frequency of the tampers not only affects the stability of paving density but also influences the vibration of the screed surface, which causes the unevenness of the paving surface [14]. Under the vibration excitation of tampers characterized by the ratios of $λ =$ {0.1, 0.2, …, 1.0} with $γ =$ 0 and 0.5, the simulation results in the same Fig. 4 show that the RMSAR in all vertical, pitch and roll motions are remarkably affected by the ratio of $λ$ in both two cases of $γ$ . Especially, all values of the RMSAR are maximum at a range of 0.6 ≤ $λ$ ≤ 0.9 corresponding the excitation frequency of tampers, 12.5 ≤ $f_{1}$ ≤ 18.7 Hz. Therefore, the compressive efficiency of the VCS is also the maximum at this frequency range. However, the paving quality and working stability are significantly reduced due to increasing the maximum paver’s pitch and roll vibrations. Observing Fig. 4(a), the vertical RMSAR is the largest at $λ =$ 0.8 ( $f_{1} =$ 16.6 Hz), concurrently, both pitch and roll RMSAR in Figs. 4(b)-(c) are slightly reduced. Thus, the excitation of tampers at $λ =$ 0.8 can significantly improve the paver’s performance. At a ratio of $λ =$ 0.8 with $γ =$ 0 and 0.5, the acceleration responses at the centre of gravity of the vibration screed are plotted as in Fig. 6.

Fig. 7Effect of the excitation of the vibrator screed

a) Vertical acceleration response

b) Pitch acceleration response

c) Roll acceleration response

Fig. 8Effect of the angular deviation α

a) Vertical acceleration response

b) Pitch acceleration response

c) Roll acceleration response

3.1.2. Effect of excitation frequency of vibrator screed

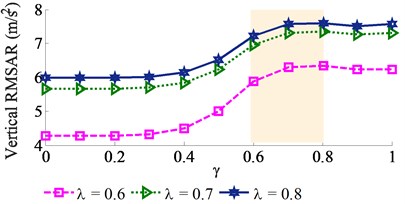
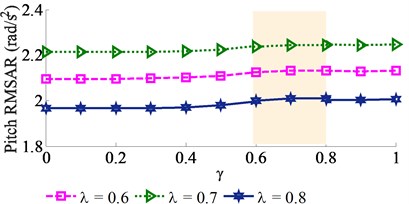
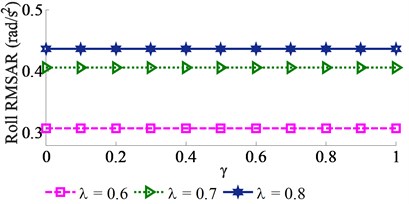
An excitation frequency range of vibrator screed characterized by the ratio of $γ =$ {0.1, 0.2, …, 1.0} with three maximum excitations of the tampers including $λ =$ {0.6, 0.7, 0.8} is respectively simulated to evaluate the impact of the excitation frequency of $f_{2}$ on the paver’s performance.

The simulation results of the vertical, pitch and roll RMSAR at the centre of gravity of the vibration screed are shown in Fig. 7. Observing Fig. 7(a), it can see that the vertical RMSAR is lightly affected at 0 ≤ $γ$ ≤ 0.5 and 0.8 ≤ $γ$ ≤ 1.0, and it is strongly increased at 0.6 ≤ $γ$ ≤ 0.8 corresponding the excitation frequency of 27 ≤ $f_{2}$ ≤ 36 Hz in all three cases of $λ =$ {0.6, 0.7, 0.8}. Contrariwise, both the pitch and roll RMSARs are insignificantly affected by the excitation of the vibrator screed, as depicted in Figs. 7(b)-(c). This is due to the vibrator screed is installed near the centre of gravity of the vibration screed. Besides, with $λ =$ 0.8, the vertical RMSAR is the largest, while the pitch RMSAR is the smallest. Thus, the paver’s performance is significantly improved at 0.6 ≤ $γ$ ≤ 0.8 with $λ =$ 0.8, corresponding the excitation frequencies of $f_{1} =$ 16.6 Hz and 27 ≤ $f_{2}$ ≤ 36 Hz.

3.1.3. Effect of the angular deviation $α$

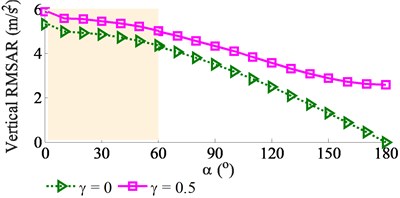
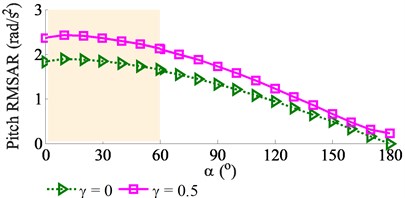
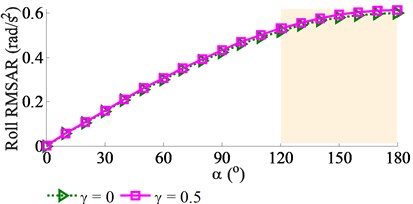
To analyze the impact of the angular deviation $α$ on the pave’s performance, a range of $α =$ {0°, 10°, 20°,…, 180°} is simulated at a ratio of $λ =$ 0.8 with $γ =$ 0 and 0.5. The results of the vertical, pitch and roll RMSAR of the vibration screed are plotted in Fig. 8.

The simulation results show that the pave’s performance is significantly affected by the angular deviation of $α$ . Both the vertical and pitch RMSARs are reduced while the roll RMSAR is enhanced with increasing the angular deviation of $α$ in both cases of $γ =$ 0 and 0.5. The maximum values of the vertical and pitch RMSARs are obtained at 0° ≤ $α$ ≤ 60°. It implies that the compressive efficiency of the VCS is the largest. Additionally, with the screed’s width 12 m, the screed’s roller vibration strongly affects on paving quality and working stability of the VCS. However, the minimum RMSAR of the screed’s roll vibration is also obtained at 0° ≤ $α$ ≤ 60°. Consequently, in order to enhance the paver’s performance, the angular deviation of $α$ in a range of 0° ≤ $α$ ≤ 60° should be chosen.

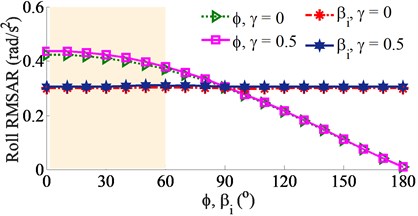
Fig. 9Effect of the angular deviations ϕ and βi

a) Vertical acceleration response

b) Pitch acceleration response

c) Roll acceleration response

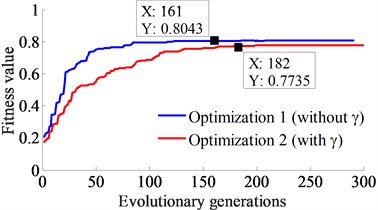
Fig. 10The curve of fitness values

3.1.4. Effect of the angular deviations $ϕ$ and $β_{i}$

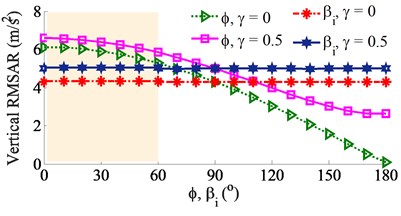
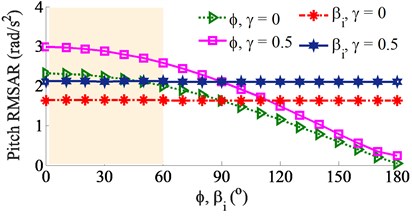
Similarly, the same initial conditions of the excitations of $λ =$ 0.8 with $γ =$ 0 and 0.5, both the angular deviations of $ϕ$ and $β_{i}$ in a range from 0° to 180° are also simulated, respectively. With the impact of the angular deviation $ϕ$ , the simulation results are plotted in Fig. 9. All the vertical, pitch and roll RMSARs are quickly decreased in both cases of $γ =$ 0 and 0.5 with increasing the angular deviation $ϕ$ , especially from 90° to 180°. The minimum RMSARs of the screed’s pitch and roll vibrations are obtained with an angular deviation range of 120^o ≤ $ϕ$ ≤ 180^o. Therefore, both the paving quality and working stability are significantly improved due to decreasing the screed shaking.

With the impact of the angular deviation $β_{i}$ , the results are also given in the same Fig. 9. Observing Figs. 9(a)-(c), it can see that the RMSARs are insignificantly affected by the angular deviation $β_{i}$ in both cases of $γ =$ 0 and 0.5, this is due to the angular deviations ( $β_{i}$ ) of excitation forces between tampers are symmetrically arranged following the tampers. Consequently, in order to enhance the compressive efficiency as well as improve the paving quality and working stability of the VCS, the angular deviation $ϕ$ in a range of 120° ≤ $ϕ$ ≤ 180° and the initial angular deviations $β_{i}$ should be used.

Based on the analysis results of the impact of the dynamic parameters on the paver’s performance, it can be deduced that when the compressive efficiency of the VCS is increased then the both paving quality and working stability is reduced and vice versa. It is difficult to simultaneously satisfy all the objectives of the compression efficiency, paving quality and working stability. Thus, to improve the paver’s performance, the dynamic parameters { $λ$ , $γ$ , $α$ , and $ϕ$ } of the VCS should be optimized based on the above analysis results.

3.2. Optimization of the VCS’s dynamic parameters

3.2.1. Optimization of dynamic parameters based on the genetic algorithm

The purpose of GA is to seek the minimum or maximum of different objectives via the computational techniques and algorithm program which is developed based on natural selection principles [23-25]. Therefore, GA is defined as finding a vector $a = {[a_{1}, a_{2}, a_{3}, \dots, a_{x}]}^{T}$ to obtain the minimum or maximum values of the vector of objective functions $G (a)$ as follow:

15

G (a) = [g_{1} (a), g_{2} (a), g_{3} (a), . . ., g_{x} (a)]^{T} .

Depending on $x_{p} (a) \leq$ 0, $p =$ 1, 2, 3,... , $P$ , $y_{q} (a) =$ 0, $q =$ 1, 2, 3,... , $Q$ , where $P$ is number of inequality constraints, $Q$ is number of equality constraints.

Basic steps of GA include the original population and encode; fitness evaluation; genetic operation and termination criterion [25]. This paper, the dynamic parameters of the VCS need to be optimized to improve the paver’s performance. Accordingly, both the minimum values of the pitch and roll RMSARs at the centre of gravity of the vibration screed ( $R M S A R_{φ}$ and $R M S A R_{θ}$ ) are chosen as the objective functions. The steps of GA are described as follows:

(i) Set up the original population and encode: To optimize the dynamic parameters of $λ$ , $γ$ , $α$ , and $ϕ$ ; four initial parameters including 0.6 ≤ $λ$ ≤ 0.9, 0.6 ≤ $γ$ ≤ 0.8, 0° ≤ $α$ ≤ 60°, and 120° ≤ $ϕ$ ≤ 180° are chosen based on the analysis results. Then, these four initial parameters are linked into a chromosome described as a vector $a = {[λ, γ, α, ϕ]}^{T}$ . Thus, the chromosomes of, $γ$ , $α$ , and $ϕ$ are encoded by $G = {[b, c, d, e]}^{T} = {[g_{i}]}_{1 \times 4}^{T}$ , $i =$ 0-20, in which:

16

\{\begin{array}{l} b = 10 λ = [60, . ., b_{i}, . ., 90], \\ c = 10 γ = [60, . ., c_{i}, . ., 80], \end{array} \{\begin{array}{l} d = α = [0, . ., d_{i}, \dots 60], \\ e = ϕ = [120, . ., e_{i}, \dots, 180], \end{array}

b_{i + 1} = b_{i - 1} + 2, c_{i + 1} = c_{i - 1} + 3, d_{i + 1} = d_{i - 1} + 6, e_{i + 1} = e_{i - 1} + 6 .

Additionally, the individuals in the original population are randomly created, and each gene in an individual is also randomly chosen by a value of 0 ≤ $g_{i}$ ≤ 20 as in Eq. (16). The size of the original population is set up to 100.

(ii) Fitness value (objective functions): In order to find the objective functions in the paper, the fitness value ( $χ$ ) is given based on Eq. (14) as follow [23, 24]:

17

χ = \frac{1}{R M S A R_{φ} + R M S A R_{θ}} .

Based on the GA program and via the mathematical model of the VCS, the individuals for higher fitness values are updated before the evolution process ends, then the optimal individuals can be achieved.

(iii) Genetic operation: The genetic operation includes the process of crossover, mutation, and selection. Herein, the probability of the crossover and mutation process used in 300 generations is 0.95 (95 %) and 0.05 (5 %). Thus, in the crossover process, 95 % of parents are selected and 5 % of children are then created with exact copies of their parents. With probability 5 % of the mutation process, each individual undergoes a mutation process in which the values of genes in a chromosome are randomly changed with a probability of 0.05 to create new genes in individuals [23]. After that, only individuals that satisfy the adaptability are selected to perform the crossover process of the next generation. When satisfying the stop condition, the crossover process ends.

Fig. 11Optimal results of vertical RMSAR at the bottom of the screed surface

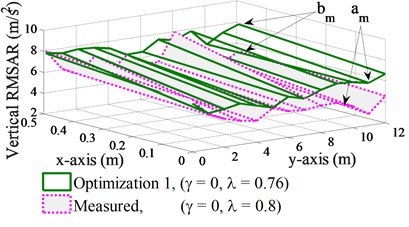
a) Without the excitation of the vibrator screed

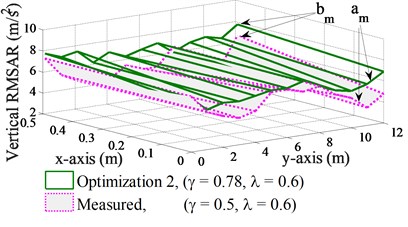
b) With the excitation of the vibrator screed

Table 3The optimal dynamic parameters of the VCS

Parameter	Initial value	Optimization 1	Optimization 2
$λ$	0.6	0.76, ( $f_{1} =$ 15.9 Hz)	0.6, ( $f_{1} =$ 12.5 Hz)
$γ$	0.6	0, ( $f_{2} =$ 0)	0.78, ( $f_{2} =$ 35.1 Hz)
$α$	0°	30.5°	55.6°
$ϕ$	90°	160.5°	145.8°

Table 4The comparison results of the paver’s performance

Without $γ$	${\bar{E}}_{1}$	${\bar{Q}}_{1}$	With $γ$ ( $λ =$ 0.6)	${\bar{E}}_{2}$	${\bar{Q}}_{2}$
Experiment ( $λ =$ 0.8)	5.23	0.93	Experiment ( $γ =$ 0.5)	5.30	0.83
Optimization 1 ( $λ =$ 0.76)	6.27	0.64	Optimization 2 ( $γ =$ 0.78)	6.16	0.62
Improvement / %	16	31	Improvement / %	14	25

3.2.2. Optimal results

To optimize the dynamic parameter of the VCS, the initial dynamic parameters of $λ = γ =$ 0.6, $α =$ 0^o, $ϕ =$ 90^o are used to simulate with the simulation time of 10 s, while other parameters are unchanged in the simulation process. The fitness value in two cases of $γ =$ 0 and 0.5 is shown in Fig. 10. The optimal results indicate that maximum values of $χ$ are limited from the 161th evolutionary generation to the end with $γ =$ 0, and from the 182th evolutionary generation to the end with $γ =$ 0.5. By recording, the optimal parameters are listed in Table 3.

Based on the optimal parameters, the vertical RMSAR at the bottom of the screed surface are respectively analyzed as follow: Without the excitation of the vibrator screed ( $γ =$ 0), the optimal parameter of $λ =$ 0.76 ( $f_{1} =$ 15.9 Hz) also closes to the ratio of $λ =$ 0.8 in the experiment, thus, the vertical RMSAR of the optimal parameters with $λ =$ 0.76 are compared with the ratio of $λ =$ 0.8 in the initial experiment, as plotted in Fig. 11(a). Besides, the indexes of the paver’s performance are also listed in Table 4. The comparison results in Fig. 11(a) show that the vertical RMSAR at the front/rear points of the screed surface is not only higher but also relatively evenly distributed under the screed surface in comparison with measured results of $λ =$ 0.8. This is the result of the dynamic parameters of $λ$ , $ϕ$ and $α$ is optimized. The comparison results in Table 4 also show that the ${\bar{E}}_{1}$ value is increased by 16 % while the ${\bar{Q}}_{1}$ value is greatly reduced by 31 % in comparison with the experiment. Thus, the paver’s performance is significantly improved.

With adding the excitation of the vibrator screed, the optimal parameter of $λ =$ 0.6 ( $f_{1} =$ 12.5 Hz) is also equal to the ratio of $λ =$ 0.6 in the experiment, concurrently the optimal value of $γ =$ 0.78 also closes to the ratio of $γ =$ 0.5 in the experiment. Thus, the results of the optimal parameters with $γ =$ 0.78 are compared with the ratio of $γ =$ 0.5 in the initial experiment at the same ratio of $λ =$ 0.6, as plotted in Fig. 11(b) and listed in the same Table 4. The optimal results show that the vertical RMSARs at the front/read points under the screed surface are higher and more stable than the measured results with the original parameters. Besides, both the ${\bar{E}}_{2}$ and ${\bar{Q}}_{2}$ values are respectively improved by 14 % and 25 %. It means that the compressive efficiency, paving quality and working stability are simultaneously improved.

Consequently, it can be concluded that the optimal parameters not only enhance compression efficiency but also improve paving quality and working stability of the asphalt paver in the paving process.

4. Conclusions

The impact of dynamic parameters of the VCS on the paver’s performance is researched and analyzed via the experiment and numerical simulation. The parameters are then optimized to improve the paver’s performance. The results can be summarized as follows:

1) Dynamic parameters of the VCS significantly affect the screed shaking and the paver’s performance. The compression efficiency is increased while the paving quality and working stability are reduced with increasing the excitation frequencies of tampers $f_{1}$ and vibrator screed $f_{2}$ and reducing the angular deviations $α$ and $ϕ$ .

2) The compression efficiency, paving quality and working stability are significantly improved by the optimal dynamic parameters of $λ$ , $γ$ , $ϕ$ , and $α$ . However, the vibration excitation of tampers $f_{1}$ and vibrator screed $f_{2}$ can be changed and depended on the operator in the paving process. Therefore, the paver’s performance can be further improved by control of the dynamic parameters.

3) Research results can add to the body of knowledge and serve as a basis for studying optimal design or control of dynamic parameters of the VCS to improve paver’s performance.

References

Luo T., Gan X., Luo W. Nonlinear dynamics simulation of compacting mechanism with double-eccentric vibrator of asphalt-paver. International Conference on Intelligent Computation Technology and Automation, 2010.

Publisher
Wan Y., Jia J. Nonlinear dynamics of asphalt-screed interaction during compaction: Application to improving paving density. Construction and Building Materials, Vol. 202, 2019, p. 363-373.

Publisher
Liu H., Jia J., et al. Investigation of paver screed on compaction characteristics of mixture. China Journal of Highway and Transport, Vol. 29, Issue 7, 2016, p. 152-157.

Search CrossRef
Jia J., Wan Y., Liu H. Parameter optimization for a compaction system of vibration screed of an asphalt paver based on a multi-objective genetic algorithm. Journal of Vibration and Shock, Vol. 36, Issue 12, 2017, p. 230-235.

Search CrossRef
Luo D., Feng Z., Wang X. Simulation and experimental study on compacting mechanism of asphalt paver. Journal of Guangxi University, Vol. 36, Issue 5, 2011, p. 729-735.

Search CrossRef
Yin C. Dynamic Study and Parameter Optimization about Screed and Tamper Mechanism of the Paver. M.S. Thesis, Southeast University 2018.

Search CrossRef
Amadore A., Bosurgi G., Pellegrino O. Analysis of hot mix asphalt compaction data by means of fuzzy clustering techniques. Construction and Building Materials, Vol. 40, 2013, p. 430-437.

Publisher
Xu Q., Chang G., et al. Influences of intelligent compaction uniformity on pavement performances of hot mix asphalt. Construction and Building Materials Vol. 30, Issue 5, 2012, p. 746-752.

Publisher
Zheng S. H., Dai Q. H., Lin S. W. Response characteristics analysis of vibrating drum in vibratory roller considering the asymmetrical hysteresis of materials. Journal of Machine Design, Vol. 33, Issue 9, 2016, p. 87-91.

Search CrossRef
Feng Z., Zhu L., Wang X., Zhao L. Dynamic simulation and parametric selection for tamping mechanism of paving machines. China Journal of Construction Machinery, Vol. 7, Issue 1, 2009, p. 26-30.

Search CrossRef
Nguyen V. L., Zhang J. R., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 8527574.

Publisher
Mollenhauer K., Wistuba M. Influence of asphalt compaction procedure on 3d deformation properties. International Journal of Pavement Engineering, Vol. 17, Issue 1, 2013, p. 1-8.

Publisher
Hou H., Wang T., et al. Investigation on the pavement performance of asphalt mixture based on predicted dynamic modulus Construction and Building Materials, Vol. 106, 2016, p. 11-17.

Publisher
Tian J., Xiao Z., Xu L. Vibrating character of compacting mechanism of paver. China Journal of Construction Machinery, Vol. 2, Issue 2, 2004, p. 201-205.

Search CrossRef
Kassem E., Liu W., Scullion T., et al. Development of compaction monitoring system for asphalt pavements. Construction and Building Materials, Vol. 96, 2015, p. 334-345.

Publisher
Kim M., Mohammad L., Phaltane P., et al. Density and SCB measured fracture resistance of temperature segregated asphalt mixtures. International Journal of Pavement Research and Technology, Vol. 10, Issue 2, 2017, p. 112-121.

Publisher
Sun J., Xu G., Wang X. Dynamics analysis and improvement of screed based on computer simulation. Journal of Multimedia, Vol. 8, Issue 5, 2013, p. 548-556.

Publisher
Jia J., Liu H., Wan Y. Dynamic characteristics modelling of the tamper-asphalt mixture interaction: application to predict asphalt mat density. International Journal of Pavement Engineering, Vol. 20, Issue 5, 2017, p. 530-543.

Publisher
Tian G., Yan W., Zhang D. Integrated designing method applied in paver attachment design. Journal of Shenyang University of Technology, Vol. 27, Issue 5, 2005, p. 481-484.

Search CrossRef
Luo D., Feng Z., Wang X. Parameter optimization for compacting system of asphalt paver based on response surface method. Journal of Vibration and Shock, Vol. 31, Issue 15, 2012, p. 92-95.

Search CrossRef
Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole Body Vibration-Part 2: General require. Technical Report ISO 2631-1:1997, International Organization for Standardization, Geneva, Switzerland, 1997.

Search CrossRef
OliveDavid J. Statistical Theory and Inference. Springer International Publishing Switzerland, 2014.

Publisher
Wang W., Song Y., Xue Y., Jin H., Hou J., Zhao M. An optimal vibration control strategy for a vehicle’s active suspension based on improved cultural algorithm. Applied Soft Computing, Vol. 28, 2015, p. 167-174.

Publisher
John H., Michael G., Gregory D. Multi-objective control optimization for semi-active vehicle suspensions. Journal of Sound and Vibration, Vol. 330, 2011, p. 5502-5516.

Publisher
Nariman Z., Salehpour M., Jamali A., and Hanghgoo E. Pareto optimization of a five-degree of freedom vehicle vibration model using a MUGA. Engineering Applications of Artificial Intelligence, Vol. 23, Issue 4, 2010, p. 543-551.

Publisher

Cited by

Influence of the Shear Process on the Compaction Success and Friction Behavior During Asphalt Paving

Leandro Harries | Stefan Böhm

(2024)

Study on paving compactness detection based on frequency domain characteristics of screed device vibration signal

Qingyun Luo | Honghai Liu | Zhongxin Xu | Ping Wu

(2024)

Optimization of Particle Distribution for Asphalt Mixtures in Screw Conveyer of Paver Based on Discrete Element Method and Response Surface Methodology

Yan Li | Min Ye | Yi Zhang | Yiding Sun | Changfeng Hao

(2023)

Development of automated control systems at the construction stage (using the example of linear objects)

P. D. Sevastyanov | A. V. Kazakov | M. V. Matveeva | A. V. Peshkov

(2023)

Application of machine learning method to control the vibration of the car’s suspension system

Huaxiang Zhou | Vanliem Nguyen | Renqiang Jiao | Yuan Huan

(2021)

Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Peiling Wang | Nguyen Van Liem | Jianrun Zhang

(2020)

About this article

Received

26 August 2019

Accepted

14 January 2020

Published

31 March 2020

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2020.20966

Keywords

vibration compaction system

asphalt paver

paver’s performance

genetic algorithm

Acknowledgements

This work has been supported by the National Key Research and Development Plan (No. 2019YFB2006402).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 18

Ameliorating vibratory roller quality based on two methods of cab’s horizontal damper and cab’s active suspension

Tianyuan Jiang, Vanliem Nguyen, Fan Zhang

Research article

2022 02 05

Kinematic and dynamic analysis of three-mass oscillatory system of vibro-impact plate compactor with crank excitation mechanism

Vitaliy Korendiy, Oleksandr Kachur, Volodymyr Gursky, Volodymyr Gurey, Nadiia Maherus, Oleh Kotsiumbas, Oleksandr Havrylchenko

Research article

2021 08 11

Analyzing the compacting energy and force distribution during the tamper-asphalt mixture interaction

Renqiang Jiao, Vanliem Nguyen, Jianrun Zhang

Research article

2020 09 30

Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Peiling Wang, Nguyen Van Liem, Jianrun Zhang

V. Nguyen and J. Zhang, “A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance,” Journal of Vibroengineering, Vol. 22, No. 2, pp. 322–336, Mar. 2020, https://doi.org/10.21595/jve.2020.20966

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2020.20966
UR  - https://doi.org/10.21595/jve.2020.20966
TI  - A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance
T2  - Journal of Vibroengineering
AU  - Zhang, Jianrun
AU  - Nguyen, Vanliem
PY  - 2020
DA  - 2020/03/31
PB  - JVE International Ltd.
SP  - 322-336
IS  - 2
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhang_2020,
	doi = {10.21595/jve.2020.20966},
	url = {https://doi.org/10.21595/jve.2020.20966},
	year = 2020,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {2},
	pages = {322--336},
	author = {Jianrun Zhang and Vanliem Nguyen},
	title = {A sensitivity analysis of the importance of the dynamic parameters on the paver's performance},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]J. Zhang and V. Nguyen, “A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance,” Journal of Vibroengineering, vol. 22, no. 2, pp. 322–336, Mar. 2020, doi: 10.21595/jve.2020.20966.

Copy IEEE

Copied to clipboard!

Zhang, Jianrun, and Vanliem Nguyen. “A Sensitivity Analysis of the Importance of the Dynamic Parameters on the Paver’s Performance.” Journal of Vibroengineering 22, no. 2 (March 31, 2020): 322–36. https://doi.org/10.21595/jve.2020.20966.

Copy Chicago

Copied to clipboard!

A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance

Abstract

1. Introduction

2. Experimental study and mathematical model

2.1. Experimental test

2.2. Experimental result and analysis

2.3. Mathematical model of the VCS

3. Simulation and discussion

3.1. Effect of the dynamic parameters

3.1.1. Effect of excitation frequency of tampers

3.1.2. Effect of excitation frequency of vibrator screed

3.1.3. Effect of the angular deviation α

3.1.4. Effect of the angular deviations ϕ and βi

3.2. Optimization of the VCS’s dynamic parameters

3.2.1. Optimization of dynamic parameters based on the genetic algorithm

3.2.2. Optimal results

4. Conclusions

References

Cited by

About this article

Related Articles

3.1.3. Effect of the angular deviation $α$

3.1.4. Effect of the angular deviations $ϕ$ and $β_{i}$