Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Wang, Peiling; Liem, Nguyen Van; Zhang, Jianrun

doi:10.21595/jve.2020.21560

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2020

Check for updates

Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Peiling Wang¹

Nguyen Van Liem²

Jianrun Zhang³

^{1, 2}School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi, 435003, China

²Faculty of Automotive and Power Machinery Engineering, Thai Nguyen University of Technology, Thai Nguyen, 23000, Vietnam

³School of Mechanical Engineering, Southeast University, Nanjing, 211189, China

Corresponding Author:

Nguyen Van Liem

Cite the article Download PDF

Downloads 949

WoS Core Citations 1

CrossRef Citations 8

Abstract

To enhance the compression performance and improve the paving quality of the VSS of the pavers, the experimental research of the VSS is performed to assess the VSS’s vibration stability under various excitations of the tampers and vibrator screed. A VSS’s dynamic model is also established to simulate and evaluate the VSS’s working performance. The root-mean-square (RMS) acceleration responses of the vertical and pitching motions at centre of gravity of the screed floor are chosen as the objective functions. In order to increase the VSS’s working performance, the dynamic parameters of the angular deviations of tampers are then controlled based on Fuzzy control. The research results indicate that the RMS value of the vertical screed motion is remarkably increased, concurrently the RMS value of the pitching screed angle is significantly reduced by controlling the angular deviations of tampers under different excitation frequencies of the VSS. Therefore, the VSS’s working performance is significantly improved in comparison without the control of the angular deviations.

Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Highlights

Improve the paving quality of the vibration screed system (VSS) is researched based on the optimal fuzzy control
The research results have been determined via the experimental research of the VSS
Results: the RMS value of the pitching screed angle is significantly reduced by controlling the angular deviations of tampers under different excitation frequencies of the VSS
Results: the VSS’s working performance is significantly improved in comparison without the control of the angular deviations
Application: Result can also be referenced to control the compaction force of soil compactors, which has not yet been considered in existing publications, to enhance vehicle's performance

1. Introduction

The vibratory screed system (VSS) of the pavers was used to pave uniformly and rapidly the asphalt mixture on the pavements. Thus, the VSS was designed by using a pair of tampers and a screed floor. The tampers were applied to compress the asphalt mixture on the pavements to obtain more uniform and tighter densities. Meanwhile, the screed floor with a width of 9 or 12 m was used to improve the smooth pavement in the paving process [1-3], as shown in Fig. 1(a). Therefore, VSS’s working performance was mainly evaluated via compression performance and paving quality [4, 5].

To analyze the compression performance of the VSS, the influence of the interaction between the compression force of tampers, mix-asphalt material, and elastoplastic ground on the VSS’s compression performance had been analyzed by some researchers [5-9]. It was found that the compression performance was mainly affected by mix-asphalt material when the elastoplastic ground obtained with its high-density. Thus, the characteristics of the mix-asphalt material were studied. The influence of the size of particles, temperature, and density of the mix-asphalt material was analyzed under the excitation of tampers [7, 10, 11]. The Fuzzy technique, compaction monitoring system, and multi-sensor infrared temperature scanning bar system were also applied to reduce the error of the unequal converge and optimize the compression density of the mix-asphalt material, respectively [8, 12, 13]. The research results indicated that the maximum compression performance could be achieved by using hot mix-asphalt under high and stable amplitude compressive forces of tampers. However, the research results also showed that the compression force of tampers was greatly affected by the dynamic parameters of the VSS, such as the excitation frequencies of tampers and vibrator screed, angular deviations of tampers, and distance of eccentric configuration of tampers [4, 6, 14, 15]. The vibration excitations of the VSS, the mass of tampers, and eccentric distance of the eccentric shafts were then optimized to improve the compression performance, respectively [3, 4, 16]. These dynamic parameters were then optimized, the optimal results showed that the maximum compression performance was obtained under the excitation frequencies of tampers ( $f$ ) from 10 Hz to 20 Hz and vibrator screed ( $f_{s}$ ) from 30 Hz to 40 Hz, especially at $f =$ 15 Hz and $f_{s} =$ 32 Hz. However, the results also indicated that the VSS’s shaking was the maximum at these excitation frequencies. Therefore, the paving quality of the VSS was strongly decreased. To reduce the VSS’s shaking, the angular deviations between adjacent tampers of the front and rear tampers ( $ϕ_{i}$ ), between right and left tampers ( $α_{i}$ ), and between the front and rear tampers ( $β$ ) were analyzed and optimized [4, 18]. The paving quality was then significantly improved. Although the researches had not yet considered under various excitation frequencies of both $f$ and $f_{s}$ , the conclusion of the researches indicated that controlling the angular deviations of the tampers could optimize the VSS’s working performance under different excitations of $f$ and $f_{s}$ .

In this study, to further enhance the compression performance and improve the paving quality of the VSS, the VSS’s working performance is researched via the experiment under various excitations of the tampers and vibrator screed. A VSS dynamic model is then established to simulate and evaluate the VSS’s vibration stability. The compression performance and paving quality are chosen as two indexes to evaluate the VSS’s working performance based on the objective functions of the RMS acceleration responses of the vertical and pitching screed motions. Based on the MATLAB/Simulink software and its Fuzzy control tools, the VSS dynamic model and angular deviations of tampers are then designed and controlled to enhance the compression performance and improve the paving quality of the VSS.

2. Experimental research of the VSS

2.1. Set-up of the test model

The vibration screed system includes eight couples of tampers excited by the vibration frequency ( $f$ ) of the tampers to compact the asphalt pavements and a screed floor excited by the mass of the eccentric configuration of the vibrator screed with the excitation frequency ( $f_{s}$ ) to smooth the asphalt pavements.

In order to investigate the VSS’s stability and paving efficiency, the experiment of the VSS is made under different excitation frequencies of tampers and vibrator screed to measure the vertical acceleration responses and their RMS values on the screed floor. The testing process is as follows: a vibration screed system with its width 12m is used for the experiment. Accelerometers ICP^® and an analysis system of Belgium LMS are applied to measure and compute the vertical acceleration responses and their RMS values on the screed floor. There are 24 sensors in which 12 sensors are installed in the front screed floor and 12 sensors are installed on the rear screed floor to determine the acceleration response at measurement points. The model of the test set-up is detailed in Fig. 1.

The measurement process is made under the different excitation frequencies of $f =$ {10 %, 20 %,..., 100 %}× $f_{m a x}$ corresponding to two different excitation frequencies of $f_{s} =$ {0 %, 50 %}× $f_{s m a x}$ . Herein, $f_{m a x} =$ 21 Hz and $f_{s m a x} =$ 45 Hz determined based on the actual parameters of the maximum angular velocities of tampers $ω_{m a x} =$ 1250 rpm and vibrator screed $ω_{s m a x} =$ 2700 rpm of the VSS are the maximum excitation frequencies of the tampers and vibrator screed, respectively. It can also be simply described based on the $f_{m a x}$ and $f_{s m a x}$ as follows:

1

\{\begin{array}{l} f = {f_{1},^{} f_{2},^{} f_{3},^{} f_{4},^{} f_{5},^{} f_{6},^{} f_{7},^{} f_{8},^{} f_{9},^{} f_{10}} \\ = \{2.1,^{} 4.2,^{} 6.3,^{} 8.4,^{} 10.5,^{} 12.6,^{} 14.7,^{} 16.8,^{} 18.9,^{} 21\} H z \\ f_{s} = \{f_{s 1},^{} f_{s 2}\} = \{0,^{} 22.5\} H z . \end{array},

Based on the measured data of the vertical acceleration responses at measurement points, their RMS values are computed via the signal processor and then displayed.

In previous studies of the VSS experiment, the acceleration response of the screed floor had only tested at three different locations on the screed floor [14] or at each measurement position [1] to evaluate the influence of the excitation frequencies of the tampers on the VSS’s stability. The above methods are simple for the experiment but difficult to accurately reflect the VSS’s stability due to the width of VSS up to 12 m. In this test method, the RMS acceleration responses at various measurement positions can be simultaneously determined, thus, the VSS’s stability and paving efficiency are easily analyzed compared with the existed researches.

Fig. 1Structure of VSS and its experimental set-up

a) Experimental set-up

b) Experimental model

2.2. Discussion of test results

Based on the measured results of the RMS acceleration responses at measurement points i on the front and rear screed floors ( $R M S_{({\ddot{z}}_{1 a})}$ and $R M S_{({\ddot{z}}_{2 a})}$ ), the RMS values at centre of gravity of the screed following the screed width are calculated by:

2

R M S_{({\ddot{z}}_{a})} = \frac{R M S_{({\ddot{z}}_{1 a})} x_{2} + R M S_{({\ddot{z}}_{2 a})} x_{1}}{x_{1} + x_{2}},

where $x_{1}$ and $x_{2}$ are the distances from the centre of gravity of the screed to measurement points $a$ at front and rear screed floors in the $x$ -direction, $a =$ 1, 2, ..., 12.

The RMS accelerations under the different excitation frequencies of tampers $f = \{f_{1}, f_{2}, \dots, f_{10}\}$ in two cases of Eq. (1) without screed excitation ( $f_{s 1} =$ 0 Hz) and (2) with screed excitation ( $f_{s 2} =$ 22.5 Hz) are plotted in Figs. 2(a)-(b).

(1) Without the screed excitation ( $f_{s 1} =$ 0 Hz), the results in Fig. 2(a) show that the RMS accelerations on the screed width are relatively symmetrical and uniform under excitations of $f < f_{5}$ . It means that the smoothness of the pavement surface is good and the paving quality is improved. However, the obtained RMS values are relatively small, thus, the compression performance is low and the asphalt density may be reduced and not uniformed.

When increasing the excitations of $f_{5} \leq f \leq f_{7}$ , the RMS results are quickly increased. The VSS’s compression performance is thus enhanced, especially at $f_{7} =$ 14.7 Hz. But the paving quality is strongly reduced due to uneven distribution of accelerations on the screed floor under the impact of $f$ .

When increasing the excitations of $f_{7} < f \leq f_{10}$ , the measured results show that the RMS values are insignificantly increased while the RMS values between the tested locations are still greatly skewed, therefore, the working performance of the VSS are insignificantly improved under the excitations of $f > f_{7}$ .

Fig. 2Experimental results under various frequency excitations of the VSS

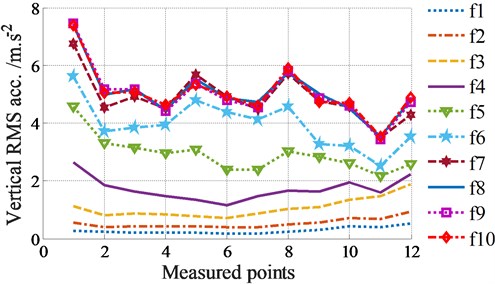
a) Without screed excitation ( $f_{s 1} =$ 0 Hz)

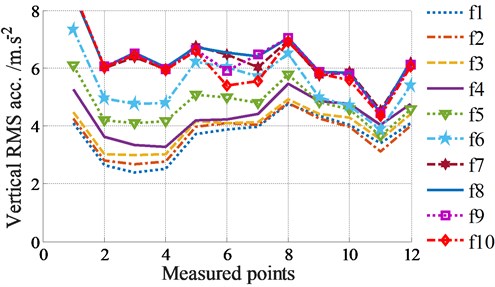
b) With screed excitation ( $f_{s 2} =$ 22.5 Hz)

(2) With the screed excitation ( $f_{s 2} =$ 22.5 Hz) added to the VSS, Fig. 2(b) indicates that the influence of the various excitation frequencies of tampers on the RMS accelerations of the screed floor is similar to the results without the screed excitation. However, due to the influence of the screed excitation $f_{s 2}$ , the RMS accelerations at the tested locations are remarkably skewed and increased in comparison with the results of without the screed excitation, especially under excitations of $f < f_{5}$ .

Based on the experimental analysis of the VSS, it can see that the excitation frequencies of both $f$ and $f_{s}$ strongly affect the VSS’s working performance. The VSS’s compression performance is maximum at $f = f_{7}$ or $f_{8}$ while the paving quality is greatly reduced at these frequencies. It is very difficult to obtain simultaneous both increasing the compression efficiency and improving the paving quality under the various excitations of both $f$ and $f_{s}$ .

The research results in Refs. [2, 5] also showed that the asphalts paver’s performance is affected not only by the vibration excitations of $f$ and $f_{s}$ but also by the angular deviations of the tampers. Thus, in order to improve the VSS’s working performance, a VSS’s dynamic model is established to control the vibration of tampers under the various excitations of $f$ and $f_{s}$ .

3. Dynamic model and vibration control of VSS

3.1. The vibration dynamic model of VSS

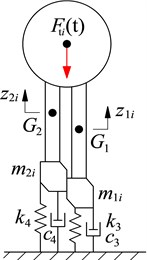
In order to study vibration and control the VSS, its mathematical model should be set-up to calculate vibration equations. Based on the VSS’s structure in Fig. 1(a), a dynamic model of the VSS is then built as in Fig. 3(a) to research the vibration characteristics of the VSS, where $m_{0}$ and $J$ are the mass and moment of inertia of the screed. $z$ and $φ$ are vertical and angular displacements at centre of gravity of the screed. $c_{1,2}$ and $k_{1,2}$ are the damping and stiffness parameters of the asphalt pavement under the screed floor. $F_{1} (t)$ and $F_{2} (t)$ are the vibration excitation forces of the screed and tamper of the VSS. $l_{1,2}$ and $l_{3,4}$ are the distances from centre of gravity of the screed to the location of vibration isolations and vibration excitations, respectively.

Fig. 3The dynamic model and vibration excitation model of the vibration screed system

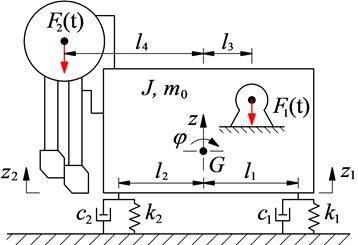
a) VSS’s dynamic model

b) Vibration excitation of tampers

Based on the dynamic model in Fig. 3(a) and application of Newton’s second law, the dynamic differential equation for the VSS is given by the following matrix form:

3

[\begin{matrix} m_{0} & 0 \\ 0 & J \end{matrix}] [\begin{array}{l} \ddot{z} \\ \ddot{φ} \end{array}] + [\begin{matrix} c_{1} + c_{2} & - l_{1} c_{1} + l_{2} c_{2} \\ - l_{1} c_{1} + l_{2} c_{2} & l_{1}^{2} c_{1} + l_{2}^{2} c_{2} \end{matrix}] [\begin{array}{l} \dot{z} \\ \dot{φ} \end{array}]

+ [\begin{matrix} k_{1} + k_{2} & - l_{1} k_{1} + l_{2} k_{2} \\ - l_{1} k_{1} + l_{2} k_{2} & l_{1}^{2} k_{1} + l_{2}^{2} k_{2} \end{matrix}] [\begin{matrix} z \\ φ \end{matrix}] = [\begin{matrix} F_{1} (t) + F_{2} (t) \\ l_{4} F_{1} (t) - l_{3} F_{2} (t) \end{matrix}] .

The vibration excitation forces of the vibrator screed $F_{1} (t)$ and tampers $F_{2} (t)$ in the $z$ -direction are respectively calculated as follows:

4

\{\begin{array}{l} F_{1} (t) = m_{s} e_{s} (2 π f_{s})^{2} s i n 2 π f_{s} t, \\ F_{2} (t) = \sum_{i = 1}^{8} F_{t i} (t), \end{array}

where $m_{s}$ , $e_{s}$ , and $f_{s}$ are the mass, distance of eccentric configuration, and vibration excitation frequency of the vibrator screed, respectively. $F_{t i} (t)$ is the vibration excitation force of tamper $i$ in the $z$ -direction.

To determine the $F_{t i} (t)$ of tamper $i$ , the dynamic model of tampers is then established as in Fig. 3(b). Where $\{z_{1 i}, z_{2 i}\}$ and $\{m_{1 i}, m_{2 i}\}$ and are the vertical displacements and masses at centre of gravity of the front and rear tampers $i$ . $c_{3,4}$ and $k_{3,4}$ are the damping and stiffness parameters of the asphalt pavement under the front and rear tampers, ( $i =$ 1, 2,..., 8).

Based on the dynamic model in Fig. 3(b) and also application of Newton’s second law, the equation of the excitation force $F_{t i} (t)$ of the tampers is determined as:

5

\{\begin{array}{l} F_{t i} (t) = m_{1 i} {\ddot{z}}_{1 i} + m_{2 i} {\ddot{z}}_{2 i} + c_{3} {\dot{z}}_{1 i} + c_{4} {\dot{z}}_{2 i} + k_{3} z_{1 i} + k_{4} z_{2 i}, \\ z_{1 i} = e_{1} s i n (2 π f t + ϕ_{i} + α_{i} + β), \\ z_{2 i} = e_{2} s i n (2 π f t + ϕ_{i} + α_{i}), \end{array}

where $\{\begin{array}{l} i = 1,3, 5,7 \\ i = 2,4, 6,8 \end{array}$ then $\{\begin{array}{l} ϕ_{i} = 0 \\ ϕ_{i} = 90 ° \end{array}$ ; $\{\begin{array}{l} i = 1,2, 3,4 \\ i = 5,6, 7,8 \end{array}$ then $\{\begin{array}{l} α_{i} = 0 \\ α_{i} = 60 ° \end{array}$ . $e_{1}$ and $e_{2}$ are the distance of the eccentric configuration of the front and rear tampers. $f$ is the vibration excitation frequency of tampers. $ϕ_{i}$ is the angular deviation between adjacent tampers of the front and rear tampers. $α_{i}$ is the angular deviation between the right tampers, $i =$ 1,2,3,4, and left tampers, $i =$ 5,6,7,8. $β$ is the angular deviation between the front and rear tampers, $β =$ 90°.

The excitation forces of the VSS in Eq. (4) are then applied to simulate the vertical and pitching acceleration responses at centre of gravity of the screed.

3.2. Evaluation index of VSS’s working performance

The influence of the vibration excitations $f$ and $f_{s}$ on the VSS’s working performance is evaluated via the vertical RMS accelerations of the screed floor in the experimental part. To evaluate the VSS’s compression performance and paving quality, the RMS acceleration responses of the vertical screed motion and pitching screed angle at centre of gravity of the screed are chosen as the evaluation indexes and described as follows:

6

\{\begin{array}{l} R M S (\ddot{z}) = \sqrt{\frac{1}{T} \int_{0}^{T} {\ddot{z} (t)}^{2} d t}, \\ R M S (\ddot{φ}) = \sqrt{\frac{1}{T} \int_{0}^{T} {\ddot{φ} (t)}^{2} d t}, \end{array}

where $\ddot{z} (t)$ and $\ddot{φ} (t)$ is the acceleration responses of the vertical screed motion and pitching screed angle at centre of gravity of the screed in the simulation time of $T$ .

Therefore, to increase compression performance and improve the paving quality of the VSS, the increase of $R M S (\ddot{z})$ and reduction of $R M S (\ddot{φ})$ are the objective functions.

3.3. Design of fuzzy control for the VSS

3.3.1. VSS’s control model

The VSS’s working performance is mainly dependent on the vibration excitations of $F_{1} (t)$ and $F_{2} (t)$ of the vibrator screed and tampers, as described in Eq. (4). Meanwhile, $F_{2} (t)$ is greatly affected by the dynamic parameters of angular deviations of { $ϕ_{i}$ , $α_{i}$ , and $β$ } part from the excitation frequency ( $f$ ) of tampers [2, 5]. In the working process of the VSS, both $f$ and $f_{s}$ frequencies can be changed and depend on the VSS’s operator, while parameters of { $ϕ_{i}$ , $α_{i}$ , and $β$ } are unchanged according to the original design. In order to increase compression performance and improve the paving quality of the VSS, the compression acceleration in the $z$ -direction needs to be increased, concurrently the VSS shaking should be minimized. Therefore, the angular deviation parameters of { $ϕ_{i}$ , $α_{i}$ , and $β$ } in Eq. (5) should be controlled based on the change of the excitation frequencies { $f$ , $f_{s}$ } and feedback accelerations { $\ddot{z} (t)$ , $\ddot{φ} (t)$ }.

The vibration control methods such as PID control, Fuzzy control, $H_{i n f}$ control, PID-Neural, Skyhook-Fuzzy, or PID-Fuzzy control [8, 18, 19] have been applied to control the mechanical vibration systems or vehicle suspension systems. The used control methods depend on the various control objects of each system. Fuzz control is the controller that does not depend on the operating conditions of the control system. It only depends on the appropriate selection of the control rules in the fuzzy inference system (FIS). Particularly, Fuzz control has the ability to control multi-objective based on its FIS [18, 20]. Based on the multi-objective functions of this study, Fuzzy control can be suitable to control the VSS’s vibrations.

To control the VSS’s vibrations, Fuzzy control is then used to calculate the optimal dynamic parameters of { $ϕ_{i}$ , $α_{i}$ , and $β$ } based on four signals of the excitation frequencies { $f$ , $f_{s}$ }, acceleration responses of the vertical motion, and of pitching angle at centre of gravity of the screed { $\ddot{z} (t)$ , $\ddot{φ} (t)$ }. Its control system model has been given in Fig. 4.

Fig. 4VSS’s control model with Fuzzy control

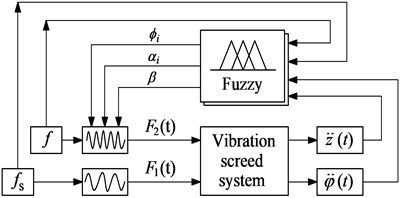
Fig. 5In-output variables of membership function

3.3.2. Fuzzy control and application

Based on the research results of the influence of the angular deviations on the VSS’s working performance [1, 4], it was found that the compression performance and paving quality were significantly improved with $ϕ_{i} =$ 60°, $α_{i} \leq$ 60°, and $β \geq$ 120°. Thus, based on the experimental results of the influence of the excitation frequencies { $f$ , $f_{s}$ } on the VSS’s working performance in Section 2.2, the boundary conditions of the control parameters are defined by:

7

\{\begin{array}{l} 0 ° \leq α_{i} \leq 30 °, \\ 120 ° \leq β \leq 150 °, \end{array} w i t h \{\begin{array}{l} f \leq f_{5} = 10.5 H z, \\ f_{s} \leq f_{s 2} = 22.5 H z, \end{array}

\{\begin{array}{l} 30 ° \leq α_{i} \leq 60 °, \\ 150 ° \leq β \leq 180 °, \end{array} w i t h \{\begin{array}{l} f_{5} < f \leq 21 H z, \\ f_{s 2} < f_{s} \leq 45 H z . \end{array}

The angular deviation parameters are then controlled based on Fuzzy control.

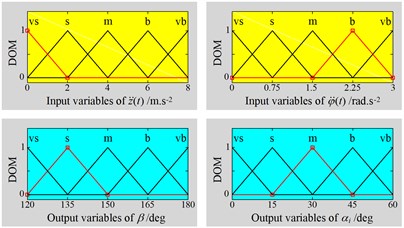
In Fuzzy control, there are three basic parts of the fuzzification interface, FIS, and defuzzification interface. Its control principle consists of the following steps: First, the input parameters are transformed into input linguistic variables via the fuzzification interface, then, input linguistic variables are deduced into output linguistic variables through FIS, and finally, the output linguistic variables are transformed back to output parameters via defuzzification interface [21]. According to the control model described in Fig. 4, four input values of { $f$ , $f_{s}$ , $\ddot{z} (t)$ , and $\ddot{φ} (t)$ } and three values of { $ϕ_{i}$ , $α_{i}$ , and $β$ } are used for Fuzzy control, respectively. However, the $ϕ_{i} =$ 60° is defined with the initial parameter of the system, thus, their in-output variables of membership function in FIS are given in Fig. 5 based on the boundary conditions in Eq. (7).

Fig. 5, in-output linguistic variables are defined by very small (vs), small (s), medium (m), big (b), and very big (vb), respectively. The shape of membership functions is used by the triangular function and the value of the degree of memberships (DOM) is between 0 and 1.

With the FIS of Fuzzy control, “If-then” rules are then built to describe the relationship between in-output language variables based on the boundary conditions of the control model and the experience of the designer. In this study, fifty control rules are given in Tables 1 and 2 and described as follows:

(1) IF 0 ≤ $f$ ≤ 10.5 and 0 ≤ $f_{s}$ ≤ 22.5Hz, $\ddot{z} (t)$ is "vs", $\ddot{φ} (t)$ is "vs" THEN $α_{i}$ is "vs" and $β$ is "vs";

(2) IF 0 ≤ $f$ ≤ 10.5 and 0 ≤ $f_{s}$ ≤ 22.5Hz, $\ddot{z} (t)$ is "s", $\ddot{φ} (t)$ is "vs" THEN $α_{i}$ is "s" and $β$ is "vs";

...

(50) IF 10.5 < $f$ ≤ 21 and/or 22.5 < $f_{s}$ ≤ 45Hz, $\ddot{z} (t)$ is "vb", $\ddot{φ} (t)$ is "vb" THEN $α_{i}$ is "vb" and $β$ is "b".

The centroid method and minimum function in FIS of Fuzzy control [20] are then used to calculate the output values via if-then rules.

Table 1The FIS’s rules with 0 ≤ f ≤ 10.5 and 0 ≤ fs ≤ 22.5 Hz

Control rules		$α_{i}$					$β$
		$\ddot{z} (t)$					$\ddot{z} (t)$
		vs	s	m	b	vb	vs	s	m	b	vb
$\ddot{φ} (t)$	vs	vs	s	s	m	m	vs	vs	s	s	m
	s	s	s	s	m	m	vs	s	s	s	m
	m	s	s	m	m	m	s	s	m	m	m
	b	m	m	m	m	m	s	s	m	m	m
	vb	m	m	m	m	m	m	m	m	m	m

Table 2The FIS’s rules with 10.5 < f ≤ 21 and/or 22.5 < fs ≤ 45 Hz

Control rules		$α_{i}$					$β$
		$\ddot{z} (t)$					$\ddot{z} (t)$
		vs	s	m	b	vb	vs	s	m	b	vb
$\ddot{φ} (t)$	vs	m	m	m	b	vb	m	m	b	b	b
	s	m	b	b	b	vb	m	m	b	vb	b
	m	m	b	b	b	vb	b	b	vb	vb	b
	b	b	b	b	vb	vb	b	vb	vb	vb	b
	vb	vb	vb	vb	vb	vb	b	b	b	b	b

Table 3Major parameters of the vibration screed system

Parameter	Value	Parameter	Value	Parameter	Value
$m_{0}$ (kg)	3 083	$m_{14,15}$ (kg)	69	$l_{1}$ (m)	0.332
$m_{11,18}$ (kg)	78	$m_{24,25}$ (kg)	72	$l_{2}$ (m)	0.163
$m_{21,28}$ (kg)	80	$c_{1}$ (kNs m^-1)	58	$l_{3}$ (m)	0.114
$m_{12,17}$ (kg)	110	$c_{2}$ (kNs m^-1)	68	$l_{4}$ (m)	0.2
$m_{22,27}$ (kg)	114	$c_{3,4}$ (Ns m^-1)	0	$e_{1}$ (m)	0.003
$m_{13,16}$ (kg)	70	$k_{1}$ (kN m^-1)	3 570	$e_{2}$ (m)	0.003
$m_{23,26}$ (kg)	71	$k_{2}$ (kN m^-1)	3 060	$e_{s}$ (m)	0.0025

4. Control results

Based on the actual structure parameters listed in Table 3, MATLAB/Simulink is applied to simulate the VSS’s dynamic equations under various vibration excitations of tampers ( $f$ ) at two cases of $f_{s 1} =$ 0 Hz and $f_{s 2} =$ 22.5 Hz. The Fuzzy control tools in MATLAB are then designed and developed to control the vibration screed system based on the boundary conditions in Eq. (7) and control rules in Tables 1 and 2.

4.1. Without the excitation of vibrator screed

The simulation results of the acceleration responses of the vertical and pitching screed motions under excitation of $f = f_{5} =$ 10.5 Hz and without $f_{s}$ are plotted in Figs. 6(a)-(b). The controlled results show that the vertical screed acceleration is increased, concurrently the pitching screed acceleration is reduced in comparison with that of the simulated results without control. This means that the VSS’s working performance is significantly improved under an excitation $f =$ 10.5 Hz of tampers.

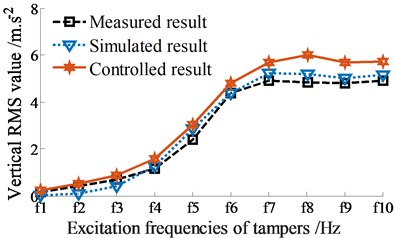
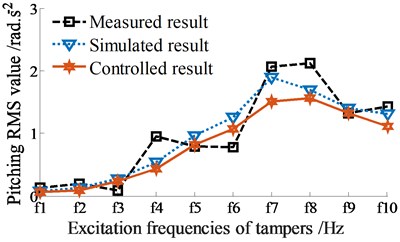
The control performance is then evaluated under various excitation frequencies of tampers, 0 ≤ $f$ ≤ 21 Hz. The measured, simulated, and controlled results of the RMS accelerations of the vertical and pitching screed motions are shown in Figs. 7(a)-(b), respectively.

Under the same experimental condition, the simulated and measured results without control show that the curves of the RMS values of the vertical and pitching RMS values at centre of gravity of the screed with simulation are similar to that of measurement. The small error between the simulated and measured values can be due to the influence of the engine vibration and error of the VSS parameters. However, the error between the measured and simulated values is negligible. Therefore, this implies that the mathematical model with the parameters of the VSS is accurate and feasible, and it is used to simulate and analyze the control results.

Fig. 6Acceleration responses at centre of gravity of screed without excitation of fs1 (fs1= 0 Hz)

a) Vibration of screed heave at $f =$ 10.5 Hz

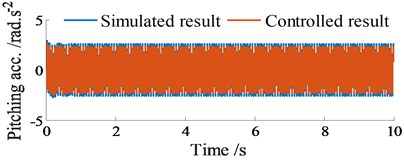
b) Vibration of screed shaking at $f =$ 10.5 Hz

Fig. 7RMS acceleration responses at centre of gravity of screed without excitation of fs1 (fs1= 0 Hz)

a) Vibration of screed heave

b) Vibration of screed shaking

The controlled results in Figs. 7(a)-(b) indicate that the RMS acceleration response of the vertical screed motion is enhanced, concurrently the RMS acceleration response of the pitching screed angle is significantly decreased under various excitation frequencies of tampers in comparison with the simulated and measured results without control. This major difference is due to the dynamic parameters of angular deviations { $ϕ_{i}$ , $α_{i}$ , and $β$ } are controlled by the Fuzzy control. Thus, the VSS vibration used Fuzzy control can increase the compression performance and simultaneously improve the paving quality.

4.2. With adding the excitation of vibrator screed

Under the same simulation condition in Section 4.1, an excitation frequency of the vibrator screed $f_{s 2} =$ 22.5 Hz is then added to the screed. The acceleration results of the vertical and pitching screed motions are plotted in Figs. 8(a)-(b).

Similarly, with the controlled results, the vertical acceleration of the screed is also increased, concurrently the pitching acceleration of the screed is reduced in comparison with the simulated results without control. Besides, the amplitude of the acceleration responses with vibrator screed excitation $f_{s 2} =$ 22.5 Hz in Figs. 8(a)-(b) is also higher and unstable in comparison with the amplitude of the acceleration responses without vibrator screed excitation $f_{s 2} =$ 0 Hz in Figs. 6(a)-(b). This issue is due to the influence of the vibrator screed excitation $f_{s 2}$ .

Besides, the RMS acceleration results of the screed are also computed and plotted in Figs. 9(a)-(b). Comparison of all the measured, simulated, and controlled results in both Figs. 7(a)-(b) and 9(a)-(b), it can see that the compression performance is maximum at $f_{7} \leq f \leq f_{8}$ . When increasing the excitation frequency $f_{8} < f \leq f_{10}$ , the compression performance is significantly reduced under all two cases without $f_{s 1}$ or adding $f_{s 2}$ of the vibrator screed. This can be due to the effect of the frictional resistance in the VSS. In order to obtain the maximum compression performance, the excitation of the tampers should be used by 14.7 ≤ $f$ ≤ 16.8 Hz, particularly at $f =$ 14.7 Hz. This research result is also close to the existed result in Ref. [4]. However, due to the screed shaking is also maximum at this excitation frequency. Therefore, paving quality is significantly decreased.

Fig. 8Acceleration responses at centre of gravity of screed with excitation of fs2 (fs2= 22.5 Hz)

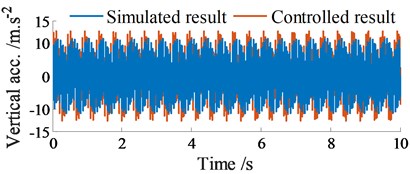
a) Vibration of screed heave at $f =$ 10.5 Hz

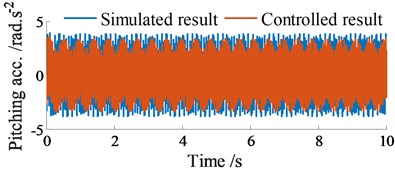
b) Vibration of screed shaking at $f =$ 10.5 Hz

Fig. 9RMS acceleration responses at centre of gravity of screed with excitation of fs2 (fs2= 22.5 Hz)

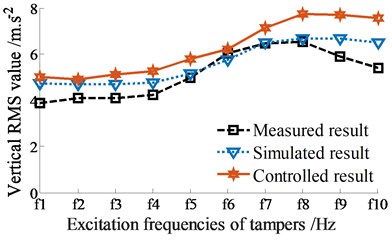
a) Vibration of screed heave

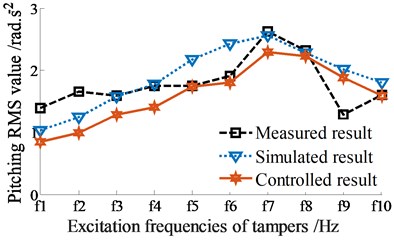
b) Vibration of screed shaking

The comparison results between the simulation and measurement in Figs. 9(a)-(b) also show that the curves of the vertical and pitching RMS values at centre of gravity of the screed without control are similar to that of measurement. Meanwhile, the controlled result of the RMS value of the vertical screed motion is also higher than that of the simulated result without control and the RMS value of the pitching screed angle is also lower than that of the simulated and measured results without control. This major difference is also due to the dynamic parameters of angular deviations { $ϕ_{i}$ , $α_{i}$ , and $β$ } are optimized by the Fuzzy control. Based on the above analysis results, it can be concluded that the compression performance is increased and the paving quality of the VSS is significantly improved under different excitation frequencies of tampers with or without the excitations of the vibrator screed. Consequently, the VSS’s working performance is significantly improved via the dynamic parameters of angular deviations of { $ϕ_{i}$ , $α_{i}$ , and $β$ } controlled by using the Fuzzy control.

5. Conclusions

1) Based on the measured and simulated results, the vibration excitations of tampers and vibrator screed greatly influence on the VSS’s working performance. The maximum compression performance is obtained at a range of 14.7 ≤ $f$ ≤ 16.8 Hz, especially at $f =$ 14.7 Hz.

2) The compression performance is increased, concurrently the paving quality is significantly improved with the angular deviations of { $ϕ_{i}$ , $α_{i}$ , and $β$ } controlled by Fuzzy control under various excitation frequencies of the VSS. Thus, the VSS’s working performance is remarkably improved by the control of angular deviations of tampers

3) The result of this study can contribute to the existing body of knowledge of the vibratory screed system of the asphalt paver and provide a reference for the optimal control of other paving machines to further improve the paving performance. Additionally, the result can also be referenced to control the compaction force of soil compactors, which has not yet been considered in existing publications [9, 17], to enhance the soil compactors’ performance.

References

Luo D., Feng Z., Wang X. Simulation and experimental study on compacting mechanism of asphalt paver. Journal of Guangxi University, Vol. 35, 2011, p. 729-735.

Search CrossRef
Liu H., Jia J., Ma C., et al. Investigation of paver screed on compaction characteristics of mixture. China Journal of Highway and Transport, Vol. 29, 2016, p. 152-157.

Search CrossRef
Jia J., Wan Y., Liu H. Parameter optimization for a compaction system of vibration screed of an asphalt paver based on a multi-objective genetic algorithm. Journal of Vibration and Shock, Vol. 36, 2017, p. 230-235.

Search CrossRef
Yin C. Dynamic Study and Parameter Optimization about Screed and Tamper Mechanism of the Paver. M.S. thesis, Southeast University, 2018.

Search CrossRef
Wan Y., Jia J. Nonlinear dynamics of asphalt-screed interaction during compaction: Application to improving paving density. Construction and Building Materials, Vol. 202, 2019, p. 363-373.

Publisher
Feng Z., Zhu L., Wang X., Zhao L. Dynamic simulation and parametric selection for tamping mechanism of paving machines. China Journal of Construction Machinery, Vol. 7, 2009, p. 26-30.

Publisher
Xu Q., Chang G., Gallivan V., Horan R. Influences of intelligent compaction uniformity on pavement performances of hot mix asphalt. Construction and Building Materials, Vol. 30, 2012, p. 746-752.

Publisher
Amadore A., Bosurgi G., Pellegrino O. Analysis of hot mix asphalt compaction data by means of fuzzy clustering techniques. Construction and Building Materials, Vol. 40, 2013, p. 430-437.

Publisher
Nguyen V., Zhang J., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 1-17.

Publisher
Hou H., Wang T., Wu S., et al. Investigation on the pavement performance of asphalt mixture based on predicted dynamic modulus. Construction and Building Materials, Vol. 106, 2016, p. 11-17.

Publisher
Mollenhauer K., Wistuba M. Influence of asphalt compaction procedure on 3d deformation properties. International Journal of Pavement Engineering, Vol. 17, 2013, p. 1-8.

Publisher
Kassem E., Liu W., Scullion T., et al. Development of compaction monitoring system for asphalt pavements. Construction and Building Materials, Vol. 96, 2015, p. 334-345.

Publisher
Kim M., Mohammad L., Phaltane P., et al. Density and SCB measured fracture resistance of temperature segregated asphalt mixtures. International Journal of Pavement Research and Technology, Vol. 10, 2017, p. 112-121.

Publisher
Jia J., Liu H., Wan Y. Dynamic characteristics modelling of the tamper-asphalt mixture interaction: application to predict asphalt mat density. International Journal of Pavement Engineering, Vol. 20, 2017, p. 530-543.

Publisher
Sun J., Xu G., Wang X. Dynamics analysis and improvement of screed based on computer simulation. Journal of Multimedia, Vol. 8, 2013, p. 548-556.

Publisher
Luo D., Feng Z., Wang X. Parameter optimization for compacting system of asphalt paver based on response surface method. Journal of Vibration and Shock, Vol. 31, 2012, p. 92-95.

Search CrossRef
Van L., Jian R. A sensitivity analysis of the importance of the dynamic parameters on the paver’s performance. Journal of Vibroengineering, Vol. 22, 2020, p. 322-326.

Publisher
Nguyen V., Zhang J., Yang X. Low-frequency performance analysis of semi-active cab’s hydraulic mounts of an off-road vibratory roller. Shock and Vibration, Vol. 2019, 2019, p. 1-15.

Publisher
Yildirim S¸. Vibration control of suspension systems using proposed neural network. Journal of Sound and Vibration, Vol. 277, 2004, p. 1059-1069.

Publisher
Ebrahimi N., Gharaveisi A. Optimal fuzzy supervisor controller for an active suspension system. International Journal of Soft Computing and Engineering, Vol. 2, 2012, p. 36-39.

Search CrossRef
Mamdani E., Assilian S. An experiment in linguistic synthesis with a fuzzy logic controller. International Journal of Man-Machine Studies, Vol. 7, 1975, p. 1-13.

Publisher

Cited by

Experiment and optimum of the asphalt paver’s parameters to ameliorate the working performance

Yundong Mei | Qian Li | Jianwei Li

(2024)

Advanced Manufacturing Processes IV

Vitaliy Korendiy | Oleksandr Kachur

(2023)

Development of automated control systems at the construction stage (using the example of linear objects)

P. D. Sevastyanov | A. V. Kazakov | M. V. Matveeva | A. V. Peshkov

(2023)

Performance of semi-active cab suspension system with different control methods

Shicheng Ni | Vanliem Nguyen

(2023)

Application of machine learning method to control the vibration of the car’s suspension system

Huaxiang Zhou | Vanliem Nguyen | Renqiang Jiao | Yuan Huan

(2021)

Study on running deviation mechanism and intelligent control of belt conveyor

Vanliem Nguyen | Renqiang Jiao | Dapeng Feng | Lang Hou

(2021)

Analyzing the compacting energy and force distribution during the tamper-asphalt mixture interaction

Renqiang Jiao | Vanliem Nguyen | Jianrun Zhang

(2021)

Effect of the mass-stiffness distribution of the vibratory roller cab on the ride quality in low-frequency region

Huan Yuan | Zhiqiang Zhang | Aoran Yang | Hao Dong

(2020)

About this article

Received

24 June 2020

Accepted

20 August 2020

Published

30 September 2020

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/jve.2020.21560

Keywords

asphalt paver dynamic model

VSS performance

vibration screed

Fuzzy control

Acknowledgements

This work has been supported by the Scientific Research Project of Education Department of Hubei Province, China (No. B2019228), Teaching and Research Project of Hubei Polytechnic University, China (No. 2018C45), Open Fund Project of Hubei Key Laboratory of Intelligent Transportation Technology and Device, Hubei Polytechnic University, China (No. 2020XY105), and National Key Research and Development Plan, China (No. 2019YFB2006402).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 18

Ameliorating vibratory roller quality based on two methods of cab’s horizontal damper and cab’s active suspension

Tianyuan Jiang, Vanliem Nguyen, Fan Zhang

Research article

2021 08 11

Analyzing the compacting energy and force distribution during the tamper-asphalt mixture interaction

Renqiang Jiao, Vanliem Nguyen, Jianrun Zhang

Research article

2021 02 16

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li, Vanliem Nguyen, Xiaoyan Guo, Yan Kang

Research article

2020 04 02

Control the ride comfort of soil compactor with semi-active seat suspension and cab’s horizontal damper

Beiping Zhang, Vanliem Nguyen, Yong Wang

P. Wang, N. V. Liem, and J. Zhang, “Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control,” Journal of Vibroengineering, Vol. 22, No. 6, pp. 1415–1426, Sep. 2020, https://doi.org/10.21595/jve.2020.21560

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2020.21560
UR  - https://doi.org/10.21595/jve.2020.21560
TI  - Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control
T2  - Journal of Vibroengineering
AU  - Liem, Nguyen Van
AU  - Wang, Peiling
AU  - Zhang, Jianrun
PY  - 2020
DA  - 2020/09/30
PB  - JVE International Ltd.
SP  - 1415-1426
IS  - 6
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Liem_2020,
	doi = {10.21595/jve.2020.21560},
	url = {https://doi.org/10.21595/jve.2020.21560},
	year = 2020,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {6},
	pages = {1415--1426},
	author = {Nguyen Van Liem and Peiling Wang and Jianrun Zhang},
	title = {Experimental research and optimal control of vibration screed system ({VSS}) based on fuzzy control},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]N. V. Liem, P. Wang, and J. Zhang, “Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control,” Journal of Vibroengineering, vol. 22, no. 6, pp. 1415–1426, Sep. 2020, doi: 10.21595/jve.2020.21560.

Copy IEEE

Copied to clipboard!

Liem, Nguyen Van, Peiling Wang, and Jianrun Zhang. “Experimental Research and Optimal Control of Vibration Screed System (VSS) Based on Fuzzy Control.” Journal of Vibroengineering 22, no. 6 (September 30, 2020): 1415–26. https://doi.org/10.21595/jve.2020.21560.

Copy Chicago

Copied to clipboard!

Experimental research and optimal control of vibration screed system (VSS) based on fuzzy control

Abstract

Highlights

1. Introduction

2. Experimental research of the VSS

2.1. Set-up of the test model

2.2. Discussion of test results

3. Dynamic model and vibration control of VSS

3.1. The vibration dynamic model of VSS

3.2. Evaluation index of VSS’s working performance

3.3. Design of fuzzy control for the VSS

3.3.1. VSS’s control model

3.3.2. Fuzzy control and application

4. Control results

4.1. Without the excitation of vibrator screed

4.2. With adding the excitation of vibrator screed

5. Conclusions

References

Cited by

About this article

Related Articles