Medical image registration based on PCA and M_PSNR

1. Introduction

In recent years, medical image registration has played an important role in clinical diagnosis and treatment planning, domestic and foreign experts and scholars in the medical image registration study phase has made many achievements, in a growing number of surgical navigation system and virtual surgery system, rapid registration is played a crucial role, at present most allocation algorithm between MRI and CT, the existing medical image registration methods mainly include two categories: the method based on gray level and based on the characteristics of the method [1].

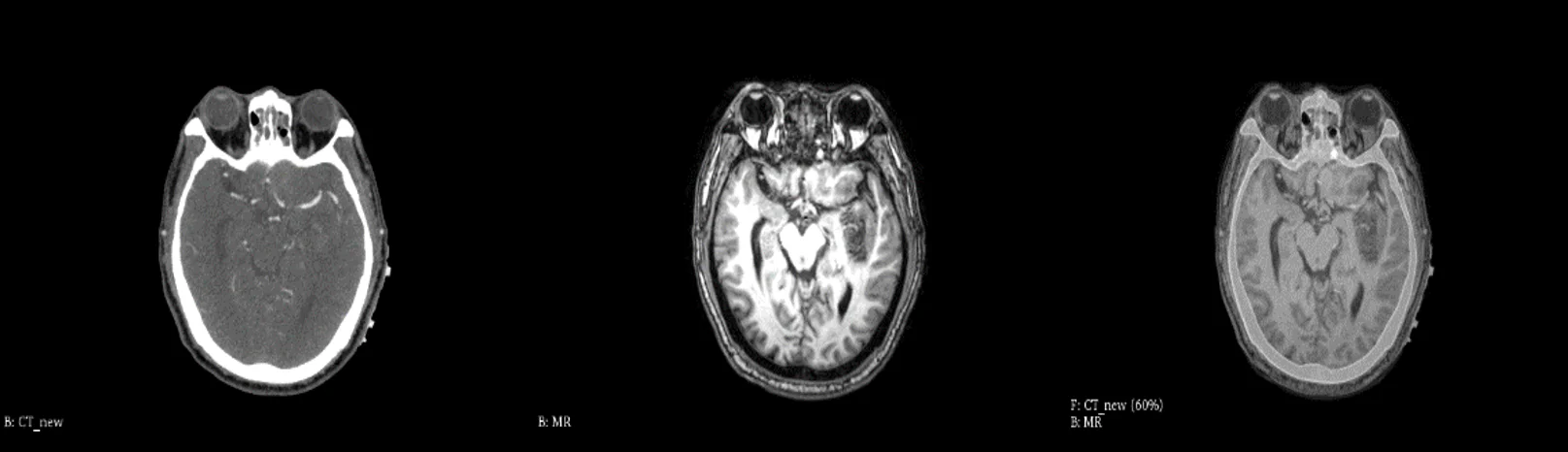
3D Slicer software in the field of medicine has strong function of Registration, the user simply import the CT and MRI data, select the General Registration Registration (Elastix) module, can quickly achieve the same patients with different mode of image Registration, also can according to the actual situation to adjust the required parameters and templates, as shown in the Figs. 1-3.

Fig. 1CT

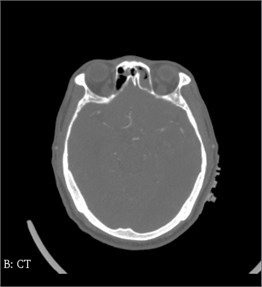
Fig. 2MR

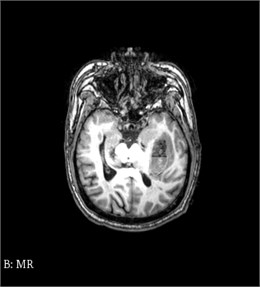
Fig. 3CT and MR registration

Medical image registration is a kind of typical problem in the field of image processing. Typically, patients receive multiple tomographic radiography for medical diagnosis. For example, images from different acquisition devices, different time, different shooting angles and so on, these are called multimode images, and multimode images are very useful in medical image analysis, because images in different modes provide supplementary information. Multimodal image registration is a method of recording the volume of different modes, for example, computed tomography (CT) and magnetic resonance (MR). Since the 20th century, medical imaging technology has experienced rapid development from static to dynamic [2], from shape to function, and from plane to three-dimensional. Combining various images to display their information on the same image and provide diversified images for clinical medical diagnosis will be a technology of great application value, while accurate and efficient image matching criteria is a major difficulty.

2. The problem of image registration based on mutual information values

Define a stereo coordinate system: the $X$-axis – along the line scan direction; the $Y$-axis – along the column scan direction; the $Z$-axis – from the bottom to the top. General with MRI image as a reference image ($R$), CT images are floating images ($F$). The image sizes of $R$ and $F$ are both $M\mathrm{*}N$, $L$ grayscale, and the grayscale values at the point $(x,y)$ are respectively $r(x,y)$ and $f(x,y)$. Under some transformation $\alpha$, the joint probability density of $R$ and $F$ images can be obtained through normalization processing $P_{FR,\alpha }(f,r)$:

where, $h_{\alpha }(f,r)$ refers to the joint gray histogram of $R$ and $F$ under the transformation of $\alpha$, and the probability density of $F$ is:

Similarly, the probability density of $R$ is:

The information contained in the gray distribution of the image is defined as the entropy of the image, denotation as $H$. In the process of medical image registration, when the space of $R$ and $F$ images is consistent, their corresponding gray mutual information $I\left(\alpha \right)$ reaches the maximum value, and the mutual information calculation formula is as follows:

where $H\left(R\right)$ is the entropy value of the reference image, $H\left(F\right)$ is the entropy value of the floating image, and $H(R,F)$ is the joint entropy of the two. That is:

According to the above equation, an optimal transformation $\tilde{\alpha }$ can be found under the rigid transformation to obtain the maximum mutual trust value [3]:

Since $\alpha$ is translation and rotation in the three-dimensional space of medical images:

where $\theta$ is the Angle of rotation as $\alpha$ change.

It can be seen that the process of finding the best transformation $\tilde{\alpha }$ is actually a multi-parameter optimization problem. Unconstrained method is usually used to find the optimal solution in such problems. By referring to the literature [4] and using the mutual information of images as the similarity test, it is necessary to use the multi-parameter optimization method of Powell [5] and simplex method to obtain the parameters in translation and rotation changes. Due to the fact that many local minima are involved in the calculation of mutual information, these optimization methods tend to get people into the trouble of local optimization. In the calculation of the optimal solution, the calculation amount is very large, the process is very tedious, and a lot of cycles and iterations are required, which consumes a lot of search time. More importantly, this algorithm needs an accurate and proper initial value. If it is not selected properly, it will consume more search time and may even cause the failure of medical image registration. Therefore, it is necessary to find a method with low registration time.

3. PCA neural network model

PCA is a tool for finding patterns of high-dimensional data, images, etc. In machine learning practice, PCA is often used to preprocess the input neural network data. PCA is the nature of the direction of maximum variance as the main characteristics, through the gathering, rotation and scaling of data in each orthogonal direction will be “related to”, which make them in different orthogonal directions without correlation, this algorithm can get rid of some low variance of dimension and dimension reduction effect, this operation can improve the convergence rate of the neural network and the overall effect.

In order to improve the registration efficiency and increase the probability of registration success, the first task is to find the optimal initial value needed for medical image registration, which can greatly reduce the search time. First, PCA neural network [6] was used to calculate the first principal direction of the feature image, and then the first principal direction of the feature image was matched with the center of mass to achieve image registration. The following are the basic methods and steps of PCA algorithm in image registration.

3.2. Calculate rotation angle

The calculation of rotation Angle is an important step in medical image registration. As long as the image is rotated, it is obvious that the rotation Angle is equal to the rotation Angle of the first main direction. The first main direction of the reference feature image ($R$) and floating feature image ($F$) was calculated by using PCA neural network method, and then the rotation Angle, namely the Angle between the two main directions, was obtained [7].

The calculation of the first principal direction requires the principal element analysis neural network method of $Oja$, which can be used to calculate the principal direction of the correlation matrix with a given random data set.

Let’s say the input matrix:

11

$x\left(k\right)=\left[\begin{array}{l}{x}_1\left(k\right)\\ x_2\left(k\right)\\ \cdots \\ x_n\left(k\right)\end{array}\right]x_n\left(k\right)\in R^n,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\left(k=\mathrm{0,1},2,\dots \right).$

It’s a zero mean random matrix.

If $C_k=x\left(k\right)x(k{)}^T$ is defined, then PCA learning algorithm of $Oja$ can be described by the following random difference equation:

12

$w\left(k+1\right)=w\left(k\right)+\eta \left[w\left(k\right)C_k-w^T\left(k\right)w\left(k\right)C_{k}w\left(k\right)\right],$

where, $\eta$ is the learning rate, and $w\left(k\right)$ meets the following formula:

13

$w\left(k\right)=\left[\begin{array}{c}{w}_1\left(k\right)\\ w_2\left(k\right)\\ \cdots \\ w_n\left(k\right)\end{array}\right].$

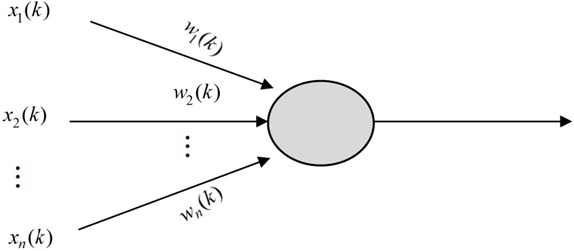
If the learning rate $\eta$ meets some basic conditions, $w$ will converge to the first main direction. The learning algorithm of PCA neural network model is shown in Fig. 4.

Fig. 4PCA neural network model algorithm schematic diagram

The reference image ($R$) and the floating image ($F$) are respectively included in the corresponding matrix $r\left(k\right)$ and $f\left(k\right)$, which satisfy the following equation:

14

$r\left(k\right)=\left(\begin{array}{l}{x}_1^r\left(k\right)\\ x_2^r\left(k\right)\end{array}\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}f\left(k\right)=\left(\begin{array}{l}{x}_1^f\left(k\right)\\ x_2^f\left(k\right)\end{array}\right).$

Using$$PCA principal component analysis neural network method under $Oja$, the first principal direction of $R$ image can be obtained:

15

$W_R={\left(r_x,r_y\right)}^T.$

And $‖W_R‖=1$, similarly, the first principal direction of image $F$ is obtained:

16

$W_F={\left(f_x,f_y\right)}^T.$

$A{b}_{\alpha }$ is the absolute value of the Angle.

And $‖W_f‖=1$.

The calculation formula of the Angle $\alpha$ between these two vectors is as follows:

17

$A{b}_{\alpha }=\left|\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}(W_R^T,W_F)\right|.$

Function $\mathrm{s}\mathrm{g}\mathrm{n}\left(x\right)$ is defined as follows:

18

$\mathrm{s}\mathrm{g}\mathrm{n}\left(x\right)=\left\{\begin{array}{l}1,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}x>0,\\ 0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}x=0,\\ -1,\mathrm{}\mathrm{}\mathrm{}x<0.\end{array}\right.$

In general, the rotation Angle is within [–30°, 30°], so the value of the rotation Angle can be obtained according to the $\mathrm{s}\mathrm{g}\mathrm{n}\left(x\right)$ function:

19

$\alpha =\left\{\begin{array}{l}\mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{f_y}{f_x}\right)\cdot A{b}_{\alpha },\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{r_y}{r_x}\right)\ne \mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{f_y}{f_x}\right),\\ \mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{r_y}{r_x}-\frac{f_y}{f_x}\right)\cdot A{b}_{\alpha },\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{r_y}{r_x}\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{f_y}{f_x}\right).\end{array}\right.$

3.5. Registration translation calculation

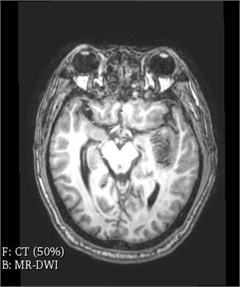
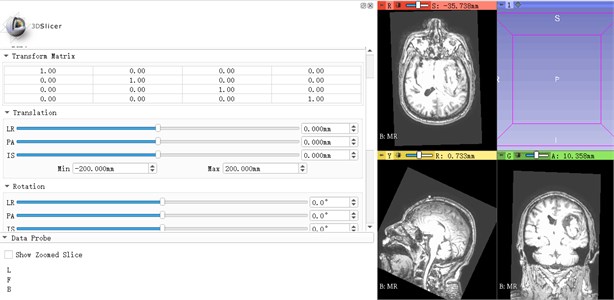
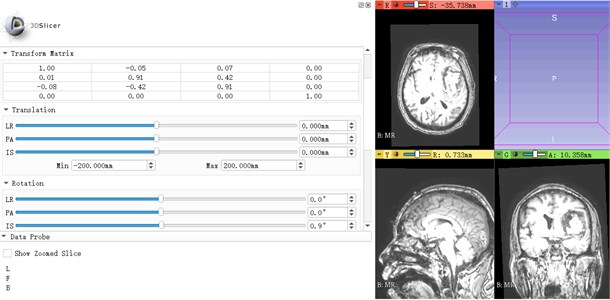
Translation and Rotation are important steps in the image registration process, and the Translation and Rotation operations in the Transforms module in 3D Slicer software can translate and rotate slices, taking MR as an example. The section was rotated and adjusted by Rotation. The axial midline adjustment (IS) and coronal midline adjustment (PA) were performed to make the yellow line of the cross line coincide with the midline, and the sagittal position was adjusted by Angle (LR). The comparison before and after translation and rotation is shown in Fig. 5.

Fig. 5MR contrast diagram before and after translation rotation

4. Image similarity test based on PSNR method

Based on the problem of mutual information value in medical image registration, it requires a large amount of calculation, a complex process and a long time, so it cannot directly reflect the difference between the reference image and the floating image as a whole. In order to evaluate the image similarity after registration more objectively, the PSNR method (image peak signal-to-noise ratio) [7] was finally adopted to test the similarity, so as to further reduce the time of image registration.

PSNR is a commonly used objective standard for evaluating images, which can directly show the gray scale difference between $R$ and $F$ on the whole. Generally, the larger the calculated PSNR is, the smaller the gray difference between $R$ and $F$ is, and the more similar the image is. On the contrary, the smaller$$PSNR is, the bigger the gray scale difference between $R$ and $F$ images is, and the bigger the difference between the two images is. The mathematical formula of is expressed as follows:

where, MSE is the mean square error between $R$ and $F$ images. Combining with Eq. (8), we can get:

Since PSNR algorithm has more advantages in terms of computational load, it is selected as the similarity test of $R$ and $F$ images, and then refers to 1 to find the best transformation of the two images, so as to maximize the PSNR value of the image after registration:

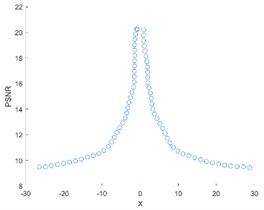
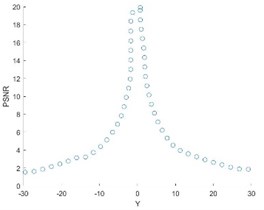
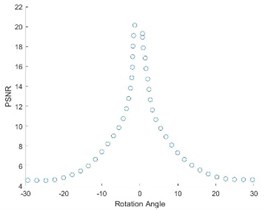
Self-registration was carried out for the $X$ direction, $Y$ direction and Angle rotation in Fig. 1, and the following PSNR change curve (Fig. 6) was obtained.

As can be seen from the Fig. 6, the PSNR curve has a break point and needs to be corrected.

Fig. 6PSNR curve

5. Improved M_PSNR method

Theoretically, the value of $\sum _{x=1}^M\sum _{y=1}^N\left(r\right(x,y)-f(x,y){)}^2$ could be 0, in which case PSND$=\mathrm{\infty }$, it is like an image registration with itself; But in the actual situation $R$ and $F$ the two images on time, $\sum _{x=1}^M\sum _{y=1}^N\left(r\right(x,y)-f(x,y){)}^2$ is impossible to be 0.

It is necessary to modify the above Eq. (22) and add a modified value $\mathrm{\Delta }d$ to obtain the improved$$PSNR, which is defined as M_PSNR algorithm. The calculation of M_PSNR method is as follows:

The optimal transformation ${\tilde{O}}_{tf}$ of the corresponding two images becomes:

According to Eq. (24), the modified value $\mathrm{\Delta }d$ is:

Because of the preconditions:

The norm of the modified value $\mathrm{\Delta }d$ is obtained:

A large number of experiments have shown that:

As a result:

Substitute $\mathrm{\Delta }d$ into Eq. (24), and get:

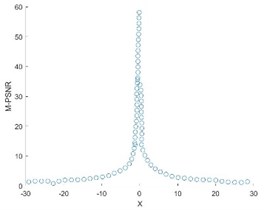
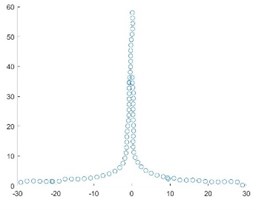
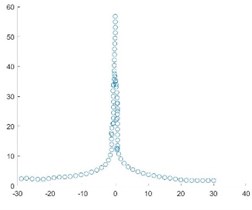
The following M_PSNR curve graph (Fig. 7) was obtained by self-registration of Fig. 1.

After adding the modified value, the M_PSNR curve is smoother, and the registered image will not show the $\mathrm{\infty }$ break point. When testing the similarity degree of images, the curve of the improved M_PSNR method is relatively smooth, and there is no breakpoint in the image after registration, and the registration speed is greatly improved. Secondly, the algorithm is simple and universal with strong portability.

6. Discussions

This paper is based on the problem of mutual information value in medical image registration. For example, when calculating the maximum gray mutual information $I\left(\alpha \right)$ [9], it involves the solution of some local minima, which requires a large amount of calculation, a tedious process and a lot of time. A method based on$$PCA neural network and M_PSNR model is proposed.

When determining the centroid coordinates of the image, the zero-order moment and the first-order moment are calculated. Then PCA neural network method was used to calculate the rotation Angle of the first principal direction, and the rotation invariance of PCA was used to get the initial value, and then the Angle between the two principal directions, namely the rotation Angle, was obtained. The initial registration value obtained [10] by this method is close to the optimal, which can reduce the search time, avoid getting into the local optimal problem when searching for the optimal rotation, and obtain better registration accuracy.

In order to further reduce the time of image registration, M_PSNR method is required to conduct similarity test for the two images and find the best transformation $O_{tf}$ of the two images, so that the M_PSNR value of the image after registration can reach the maximum. At the same time, an improved M_PSNR method was proposed. The calculation amount was about the same, but the modified $\mathrm{\Delta }d$ was added to improve the registration speed.

Fig. 7M_PSNR curve

7. Conclusions

In conclusion, for the registration methods used for mutual information, the image registration methods used in this paper have more advantages. The larger the image size, the higher the registration effect. PCA neural network model was used to complete the registration of its first principal direction and the centroid of the image, and then the improve PSNR d method was used to test the similarity of $R$ and $F$ images. A rigid registration method based on PCA neural network and M_PSNR was proposed, which was simple and efficient. CT and MRI image registration will provide doctors with more medical information, including diagnosis and treatment information. Accurate registration is helpful for diagnosis and treatment of craniocerebral tumor and other problems [12].