Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure

Li, Cong; Yang, Guolai; Yu, Qingbo; Sun, Quanzhao

doi:10.21595/jve.2021.21867

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2021

Check for updates

Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure

Cong Li¹

Guolai Yang²

Qingbo Yu³

Quanzhao Sun⁴

^{1, 2, 4}School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China

³China Aerospace Science and Industry Nanjing Chenguang Group, Nanjing, China

Corresponding Author:

Guolai Yang

Cite the article Download PDF

Downloads 1189

WoS Core Citations 2

CrossRef Citations 2

Abstract

In view of the influence of projectile-barrel coupling on tank firing accuracy, a finite element model of projectile-barrel coupling based on vibration theory was established. By defining user subroutines to simulate the change of the physical field of interior ballistics, the load condition under which the propellant gas radial pressure acts on the inner wall of the barrel and varies with the motion of the projectile is realized. On this basis, the dynamic characteristics of projectile-barrel coupling considering the radial effect of propellant gas pressure were studied. The reference targets such as cradle, projectile and muzzle were selected for analysis, and compared with the situation without considering the radial effect of propellant gas pressure. The results show that the motion trend of the projectile in the bore and the response law of muzzle vibration change greatly when considering the radial effect of propellant gas pressure and these changes may seriously affect the law of projectile dispersion. The radial effect of propellant gas pressure can cause stronger dynamic response, which cannot be ignored in the simulation of artillery firing process. This work provides a practical reference for further study of tank firing accuracy.

Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure

Highlights

Provide a convenient method of secondary development of subroutine in ABAQUS program to simulate the change of the physical field of interior ballistics, the load condition under which the propellant gas radial pressure acts on the inner wall of the barrel and varies with the motion of the projectile is realized.
After considering the radial effect of propellant gas, more real kinetic results can be obtained.
The dynamic characteristics of projectile-barrel coupling change greatly when considering the radial effect of propellant gas pressure and these changes may seriously affect the law of projectile dispersion.
Probing into the influence of the radial effect of propellant gas pressure on muzzle vibration is helpful to establish an accurate launch environment model, which is used to explore the key factors affecting the firing accuracy of artillery.

1. Introduction

With the sharp increase of the contradiction between maneuverability and power, under the condition of high-speed maneuver, the stability of the tank body deteriorates, the barrel disturbance increases, and the incentive of the projectile to the barrel increases, which seriously affects the firing accuracy of the tank. Therefore, it is particularly important for tank firing accuracy to study the influence of projectile excitation on muzzle vibration.

Due to the clearance between the projectile and the barrel and the existence of copper band, bourrelet and copper band will contact and collide with the inner wall of the barrel, which will affect not only the motion of the projectile, but also the flexible motion of the barrel, and greatly affect the firing accuracy of the gun [1].

Many scholars have studied the problem of projectile-barrel coupling. Reference [2] studied the influence of projectile-gun coupling system on muzzle vibration by using a cyclic coupling model of interior ballistics. In reference [3], the dynamic equations of projectile-barrel coupled system considering the effect of rigid-flexible coupling during the artillery launching process are established, and the proposed contact force model is employed to quantify the contact responses between barrel and bourrelet. In reference [4], a method with which the force can be transferred by the analog barrel was presented, based on the rigid-flexible coupling dynamics model including virtual substances. In order to study the vibration characteristics of the barrel excited by the moving projectile during the gun firing, reference [5] established the moving projectile-elastic barrel coupling vibration equation considering the initial deflection of the barrel, and analyzed the effect of projectile velocity and mass on the muzzle vibration characteristics. However, the above studies focus on the contact collision between the projectile and the barrel, ignoring the influence of the propellant gas effect. However, in the process of firing, not only the projectile will contact and collide with the inner wall of the barrel, but also the high pressure propellant gas will scour the inner wall of the barrel, resulting in a certain elastic vibration of the barrel, which has a direct impact on the initial motion attitude of the projectile, and then affects the firing accuracy [6, 7].

Therefore, based on previous studies, this paper studies the muzzle vibration characteristics when firing armour-piercing projectiles under the condition of zero firing angle of tank, considering the radial effect of propellant gas pressure, and makes a comparative analysis with the situation without considering the radial effect of propellant gas pressure.

2. Projectile-barrel coupling dynamic model

2.1. Load analysis of barrel

The barrel is simplified as an equal cross-section Euler-Bernoulli beam with one end fixed and the other free [8]. It is assumed that the projectile moves along the axis of the bore. When the projectile moves in the bore, the barrel is subjected to propellant gas radial pressure and the contact collision force of the projectile. The mechanical model is shown in Fig. 1.

Fig. 1Simplified schematic diagram of actual loading of barrel

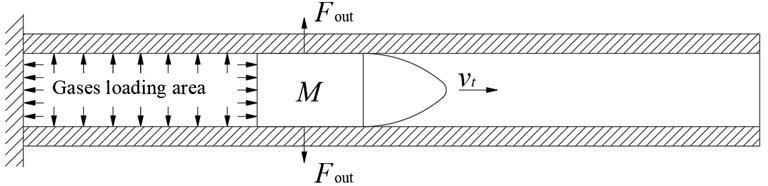
Considering the damping and the projectile inertia effect, according to D’Alembert ‘s principle [9], the equation of radial motion of the projectile under the action of gunpowder gas is obtained:

1

\frac{\partial^{2}}{\partial x^{2}} [E I (x) \frac{\partial^{2}}{\partial x^{2}} y (x, t)] + ρ A (x) [\frac{\partial^{2}}{\partial t^{2}} y (x, t) + 2 H \frac{\partial}{\partial t} y (x, t)] = F,

where $E I (x)$ is the bending stiffness of the barrel, $A (x)$ is the cross-sectional area of the barrel, and $ρ$ is the mass density per unit length of the barrel, $H$ is the velocity attenuation coefficient of the barrel, and $y (x, t)$ is the deflection at t moment at the position of the barrel, $F$ is the loading condition of the barrel.

2.2. Finite element model

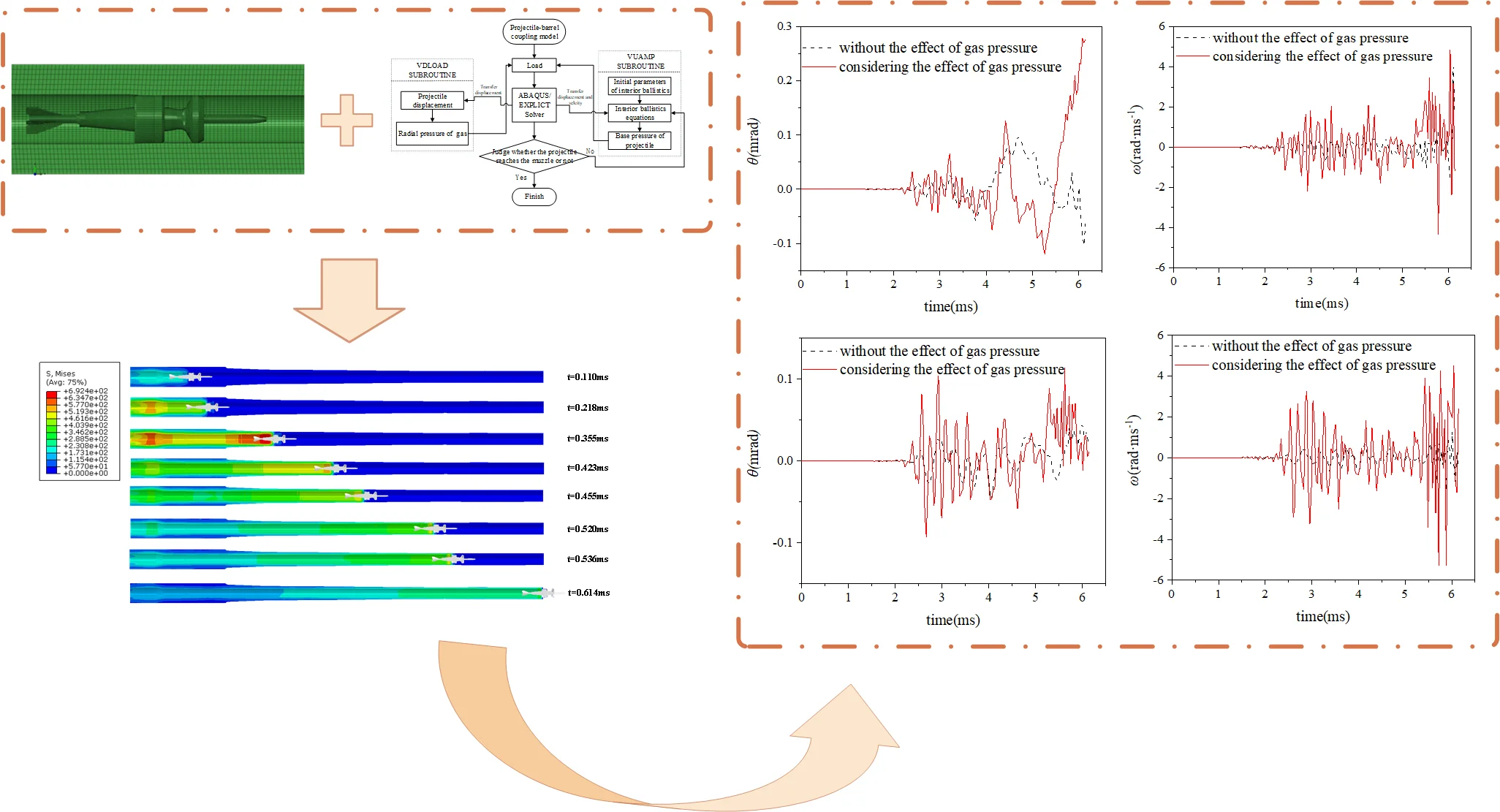
The finite element model of the whole vehicle is shown in Fig. 2, and the finite element model of projectile and barrel is shown in Fig. 3. The barrel, projectile and copper band are all divided by eight-node hexahedral elements (C3D8R). In the finite element model, the relationship between the copper band and the inner wall of the barrel is defined as point-to-surface contact, and the bourrelet and the inner wall of the barrel, and the recoil part and the cradle are defined as surface-to-surface contact, all of which are dealt with by the penalty function method. The deformation of the projectile is not the main object of study, so the projectile is modeled as rigid body and the copper band is modeled as elastic-plastic body.

Fig. 2The finite element model of the whole vehicle

Fig. 3The finite element model of projectile and barrel

2.3. Simulation of physical field variation of interior ballistics

During the movement of the projectile in the bore, there is an interaction between the barrel, the projectile and the propellant gas, which is a complex process of physical field change [10]. On the one hand, propellant gas pushes the projectile and recoil to complete the interior ballistic process. On the other hand, propellant gas will exert pressure on the inner wall of the barrel after the projectile, and the pressure will change dynamically with the movement of the projectile. Therefore, through the secondary development of ABAQUS software, VUAMP and VDLOAD subroutines are written based on FORTRAN programming language to simulate the changes of interior ballistic physical field [11].

2.3.1. Simulation of propellant combustion process

At present, most scholars use the method of loading the measured inner chamber pressure curve at the bottom of the projectile to simulate the process of propellant gas driving the motion of the projectile in the bore, but this method is equivalent to calculating the friction work and plastic work twice, and incorrect results will be obtained. In order to accurately describe the combustion process of gunpowder, the interior ballistic thrust subroutine (VUAMP), is used to provide the pressure at the bottom of the projectile. The interior ballistic model is based on the classical interior ballistic model of mixed charge based on thermodynamics, and its mathematical model can be described as follows:

2

\{\begin{matrix} ψ_{i} = χ_{i} Z_{i} (1 + λ_{i} Z_{i} + μ_{i} Z_{i}^{2}), \\ \frac{d Z_{i}}{d t} = \frac{u_{1 i}}{e_{1 i}} p^{n^{*}}, \\ φ m \frac{d v}{d t} = S p, \\ S p (l_{ψ} + l) = \sum_{i = 1}^{n} f_{i} m_{i} ψ_{i} - \frac{θ}{2} φ m v^{2}, \\ \frac{d l}{d t} = v, \end{matrix}

where $l_{ψ} = l_{0} [1 - \sum_{i = 1}^{n} \frac{Δ_{i}}{ρ_{p i}} (1 - ψ_{i}) - \sum_{i = 1}^{n} α_{i} Δ_{i} ψ_{i}]$ , $i$ is the kind of propellant ( $i = 1, 2, \dots, n$ ); $ψ_{i}$ is the percentage of propellant burned; $χ_{i}$ and $μ_{i}$ are the shape parameters of the propellant; $Z_{i}$ is the relative burned thickness, $u_{1 i}$ is the burning rate, and $n^{*}$ is the burning rate index; $φ$ is the secondary power factor; $p$ is the powder gas pressure, $m$ is the projectile mass, $l$ is the projectile travel, and $v$ is the projectile velocity; $S$ is the gun barrel cross-sectional area, $θ$ is the heat ratio, $l_{0}$ ( $l_{ψ}$ ) is the chamber (free) volume-to-bore area ratio; $f_{i}$ is the propellant force, $ρ_{p i}$ is the propellant density, $e_{1 i}$ is the propellant thickness, $α_{i}$ is the powder gas covolume, $Δ_{i}$ is the loading density, and $m_{i}$ is the propellant mass.

The relative burned thickness $Z_{i}$ can be solved by fourth-order Runge-Kutta method, projectile velocity $v$ and projectile trave $l$ can be read directly by sensor in ABAQUS, and propellant gas pressure $p$ can be solved by bringing $v$ and $l$ into Eq. (2).

2.3.2. Realize the loading of propellant gas effect

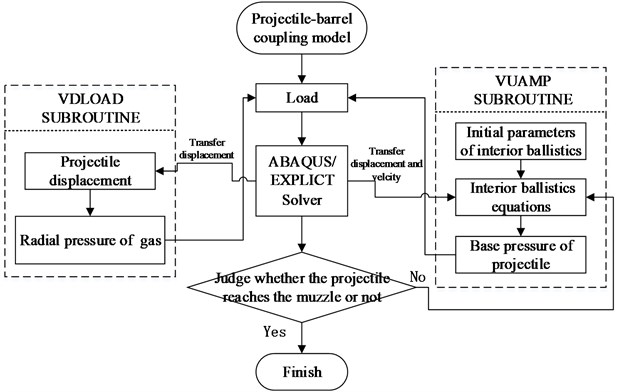
The radial pressure of propellant gas acting on the inner wall of the barrel will dynamically change in the post-projectile area with the motion of the projectile. Therefore, the subroutine (VDLOAD) is used to simulate the load acting on the barrel. When the VUAMP subroutine is used to load the projectile, the axial displacement of the projectile along the barrel is continuously read by the ABAQUS internal sensor and transmitted to the VDLOAD subroutine, thus the radial loading of the inner wall of the barrel is realized. Fig. 4 is the flow diagram of the implementation process by subroutine.

Fig. 4The calculation flow diagram

3. Analysis of numerical simulation results

3.1. Dynamic response process of barrel stress

Fig. 5 selects the barrel stress cloud images at three time nodes, from which we can see that the projectile divides the space in the bore into the high pressure area behind the projectile and the normal pressure area in front of the projectile, and the high stress of the barrel is mainly distributed in the rear area. And the loading area of the barrel behind the projectile changes dynamically with the motion of the projectile, which realizes the dynamic loading of the radial pressure of the propellant gas on the barrel. It shows that the method of subroutine loading can well describe the actual load conditions.

Fig. 5Dynamic process of stress in the inner wall of barrel

3.2. Analysis of projectile motion in bore

The in-bore motion time of armor-piercing projectile is 6.14 ms, and the calculated velocity curve of the projectile is shown in Fig. 6. After loading the firing load, the projectile speed increases rapidly. After moving 6.14 ms in the bore, the projectile moves to the muzzle position. Table 1 shows the comparison between the simulation and experimental results of the initial velocity of the projectile when it comes out of the muzzle. The simulation results show that the initial velocity of the projectile is about 1744.1 m/s. The initial velocity of the armor-piercing projectile measured by experiments at normal temperature is about 1744.5 m/s [12]. The difference between the simulation value and the experimental value is very small, and the error of simulation calculation is about 0.02 %. This shows that the projectile-barrel coupling model considering the radial effect of propellant gas pressure has a certain credibility, and more in-depth research and analysis can be carried out based on this model.

Fig. 6Velocity of projectile in bore

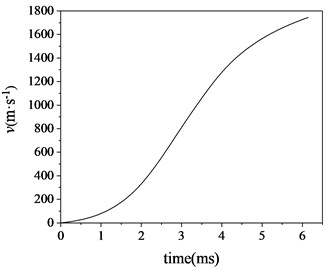
Table 1Comparison between calculated initial velocity and experimental initial velocity of projectile

Simulation and experimental results	Projectile initial velocity / (m/s)
Simulation results	1744.1
Experimental results	1744.5
Relative error	0.02 %

3.3. Load analysis of cradle

Because the pressure of propellant gas acts on the inner wall of the barrel, the inner wall of the barrel will produce a certain elastic deformation. The elastic deformation of the inner wall of the barrel will cause the expansion of the inner chamber to a certain extent, which will make the barrel and bush fit more closely, and then affect the coordination relationship between the barrel and the cradle. Because the barrel will have an impact on the cradle during the recoil motion, it can be seen from the stress change curve on the surface of the inner cylinder shown in Fig. 7 that after considering the radial pressure of gunpowder gas, the load of the inner cylinder of the cradle fluctuates greatly. And the cradle is connected to the trunnion to play a pitching role, and its large load fluctuation may aggravate the disturbance of the barrel. Fig. 8 shows the comparison of the angular velocity in the vertical direction of the cradle considering the radial effect of propellant gas and only considering the coupling of projectile and barrel.

Fig. 7Stress curve of inner cylinder of cradle

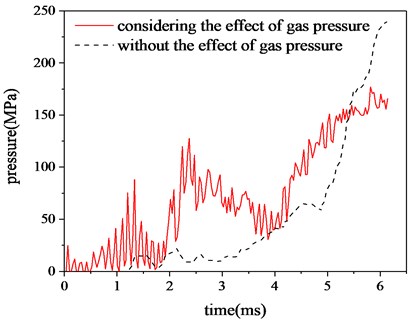
Fig. 8Vertical angular velocity of cradle

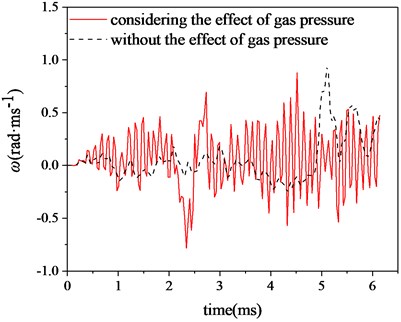
It can be clearly seen from Fig. 8 that the angular frequency in the vertical direction of the cradle is faster and the amplitude is relatively larger when considering the radial effect of propellant gas pressure than only considering the projectile-barrel coupling. Therefore, under the influence of the radial effect of propellant gas pressure, the shaking of the cradle is more intense, and the action on the barrel will inevitably aggravate the disturbance of the barrel, and then affect the firing accuracy.

3.4. Analysis of muzzle vibration response

Under the influence of the radial effect of propellant gas pressure, the disturbance of the barrel increases, and the contact collision between the projectile and the barrel becomes more intense. In order to further explore the law of the swing of the projectile in the bore, Fig. 9 and Fig. 10 show the curve of the central point of the bourrelet moving with time in the vertical direction and horizontal direction during the movement of the projectile in the bore. It can be clearly seen that after considering the radial effect of propellant gas pressure, the motion attitude of the projectile in the bore changes greatly, especially when the projectile comes out of the muzzle, the vertical displacement of the projectile is quite different. Table 2 shows the comparison of the absolute value of the vertical displacement of the bourrelet of the projectile when the projectile comes out of the muzzle. It can be seen that under the influence of the radial effect of propellant gas pressure, compared with only the coupling of projectile and barrel, the relative error of the absolute value of the vertical displacement of the projectile is 66.67 % when the bourrelet of the projectile comes out of the muzzle. This error is mainly caused by the different excitation of the muzzle vibration to the projectile when the projectile comes out of the muzzle, so it is necessary to analyze the muzzle vibration.

The muzzle center point is selected as the observation point, and the muzzle angular displacement and angular velocity curves shown in Figs. 11-14 are obtained. It can be clearly seen from the figure that after considering the radial effect of propellant gas pressure, compared with the situation without considering the radial effect of propellant gas pressure, the muzzle vibration is intensified, not only the muzzle swings faster, but also the vibration amplitude is also increased. Especially when the projectile approaches the muzzle position, the muzzle vibration is more intense, which will have a great impact on the projectile flight attitude when the projectile comes out of the muzzle, and then affect the firing accuracy. What has a great influence on the firing accuracy is the angular displacement of the Vertical direction of the muzzle when the projectile comes out of the muzzle, as shown in Table 3. When the projectile comes out of the muzzle, after considering the radial effect of propellant gas pressure, the absolute value of muzzle angular displacement is 0.276 mrad, while the absolute value of muzzle angular displacement only considering projectile and barrel coupling is 0.063 mrad. The relative error is 338.10 %. Obviously, under the influence of the radial effect of propellant gas pressure, the disturbance of the muzzle is larger, and the contact collision between the projectile and the flexible barrel has an obvious influence on the muzzle vibration state, which will directly affect the projectile dispersion. Therefore, considering the radial effect of propellant gas, it is very necessary to study the firing accuracy of the tank.

Table 2Comparison of the absolute value of the vertical displacement of bourrelet

Conditions	Absolute value of vertical displacement of bourrelet / (mm)
Considering the effect of gas pressure	0.130
Without the effect of gas pressure	0.078
Relative error	66.67 %

Fig. 9Vertical displacement of bourrelet

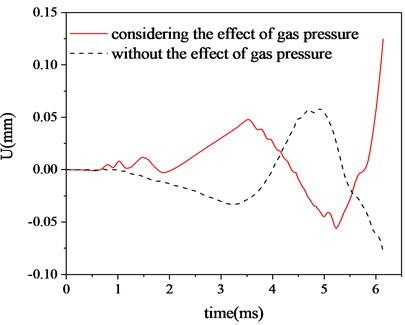
Fig. 10Horizontal displacement of bourrelet

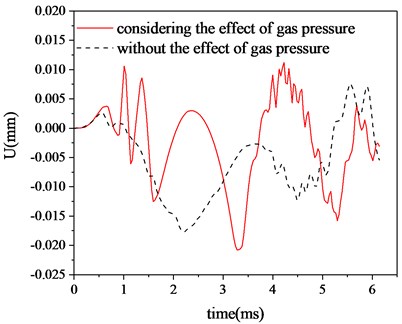
Fig. 11Vertical angle displacement

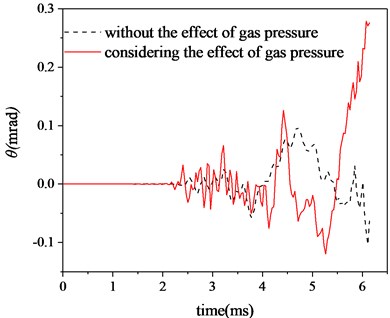
Fig. 12Vertical angular velocity

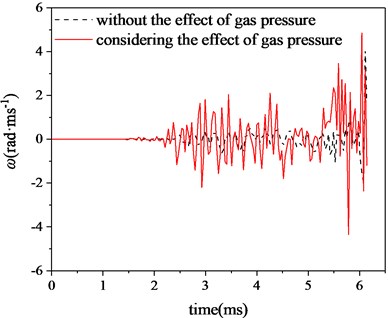
Fig. 13Horizontal angular displacement

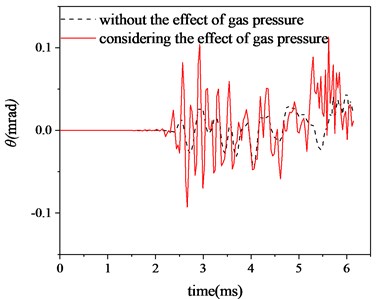
Fig. 14Horizontal angular velocity

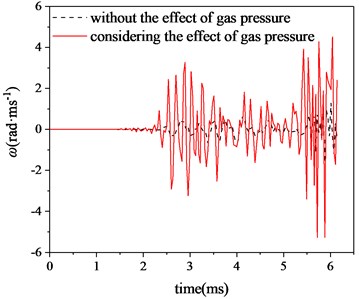
Table 3Comparison of absolute value of angular displacement of muzzle

Conditions	Absolute value of angular displacement of muzzle / (mrad)
Considering the effect of gas pressure	0.276
Without the effect of gas pressure	0.063
Relative error	338.10 %

4. Conclusions

From the point of view of tank firing accuracy, this paper studies the influence on the vibration characteristics of projectile-barrel coupling under the impact of high pressure propellant gas on the basis of the existing tank firing dynamics model based on projectile-barrel coupling. With the help of the user-defined subroutine provided by the finite element software, the correlation process between the in-bore motion of the projectile and the classical interior ballistic gunpowder combustion is realized, and the problem of radial pressure dynamic loading of propellant gas in the bore is realized at the same time. Through the comparative analysis of the dynamic response of the barrel in the numerical simulation environment with or without gas pressure radial effect, the following conclusions can be drawn:

1) In the process of tank launch, under the influence of the radial effect of propellant gas pressure, the coordination relationship between barrel and cradle is changed, which aggravates the impact of barrel on cradle during recoil.

2) Compared with only considering the coupling of projectile and gun, after considering the radial effect of propellant gas pressure, the motion attitude of the projectile in the bore changes greatly, and the impact of the projectile on the barrel is severer.

3) From the law of muzzle vibration, it can be seen that after considering the radial effect of propellant gas pressure, the disturbance amplitude of muzzle is very different from the situation without considering the radial effect of propellant gas pressure. When the projectile comes out of the muzzle, the disturbance of the muzzle will affect the flying attitude of the projectile, and this error will directly affect the dispersion law of the projectile.

In order to explore the key parameters that affect the tank firing accuracy, an accurate launch environment model should be established. However, only considering the coupling of projectile and barrel, there is no influence of propellant gas effect on the whole tank launch process, so it is impossible to accurately simulate the actual launch environment. Therefore, it is necessary to consider the radial effect of gunpowder gas pressure.

References

Ge J. L., Yang G. L. A study on the projectile-barrel coupling problem considering the initial deflection due to gravity of tube. Proceedings of the 3rd International Conference on Mechanical Engineering and Mechanics, Vol. 1, 2009, p. 718-723.

Search CrossRef
Qian L. F., Chen G. S. The uncertainty propagation analysis of the projectile-barrel coupling problem. Defence Technology, Vol. 13, Issue 4, 2017, p. 229-233.

Publisher
Ma J., Chen G. S., Ji L., Qian L. F., Dong S. A general methodology to establish the contact force model for complex contacting surfaces. Mechanical Systems and Signal Processing, Vol. 140, 2020, p. 106678.

Publisher
Chen S. Y., Wang L. M., Shi W. Dynamic analysis of contact/impact in projectile-barrel rigid-flexible coupling model. Journal of Naval University of Engineering, Vol. 25, Issue 4, 2013, p. 97-102.

Search CrossRef
Di C. C., Qin J. Q., Fang Y., Yang Y. L. Analysis of vibration characteristics of the projectile-barrel coupling system considering the initial deflection of the barrel. Journal of Mechanical Strength, Vol. 47, Issue 2, 2019, p. 504-508, (in Chinese).

Search CrossRef
Gimm H. I., Cha K. U., Cho C. K. Characterizations of gun barrel vibrations of during firing based on shock response analysis and short-time Fourier transform. Journal of Mechanical Science and Technology, Vol. 26, Issue 5, 2012, p. 1463-1470.

Publisher
Procházka S., Seman P., Vídeňka M. Deformation of the cannon barrel when projectile goes by muzzle. Proceedings of 9th Symposium on Weapon Systems, 2009.

Search CrossRef
Zhang X. B., Wang Y. Z. Analysis of dynamic characteristics for rarefaction wave gun during the launching. Journal of Applied Mechanics, Vol. 77, Issue 5, 2010, p. 1003-1013.

Publisher
Siddiqui S. A., Golnaraghi M. F., Heppler G. R. Large free vibrations of a beam carrying a moving mass. International Journal of Non-linear Mechanics, Vol. 38, Issue 10, 2003, p. 1481-1493.

Publisher
Wang L. Q., Yang G. L., Xiao H., Sun Q. Q., Ge J. L. Interval optimization for structural dynamic responses of an artillery system under uncertainty. Engineering Optimization, Vol. 52, Issue 2, 2020, p. 343-366.

Publisher
ABAQUS User’s Manual. Version 6.6, Hibbitt, Karlsson and Sorensen Inc, Michigan, 2006.

Search CrossRef
Liu F. F., Rui X. T., Yu H. L., Zhang J. S., Gu J. J. Influence of barrels’ flexibility on the launch dynamics of tank during marching fire. Vibration and Shock, Vol. 35, Issue 2, 2016, p. 58-63+96, (in Chinese).

Search CrossRef

Cited by

Study on the coupling calculation method for the launch dynamics of a self-propelled artillery multibody system considering engraving process

Shujun Zhang | Xiaoting Rui | Hailong Yu | Xiaoli Dong

(2024)

General design principle of artillery for firing accuracy

Linfang Qian | Guangsong Chen | Minghao Tong | Jinsong Tang

(2022)

About this article

Received

09 January 2021

Accepted

22 March 2021

Published

31 March 2021

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2021.21867

Keywords

projectile-barrel coupling

the radial effect of propellant gas pressure

user subroutine

muzzle vibration and firing accuracy

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 11 26

Modeling and simulation on engraving process of projectile rotating band based on two-phase flow interior ballistic

Zhen Wang, Liqun Wang, Guolai Yang

Research article

2020 06 29

Study on dynamic response of moving tank under the action of temperature field

Yuze Ma, Guolai Yang

Research article

2019 08 15

Research on vibration characteristics of a multi-barrel artillery

Yingfeng Wu, Qingsi Cheng, Guolai Yang, Jinsong Dai

Research article

2019 03 31

Launching dynamic analysis for tank on the move based on dynamic simulation

Yu Chen, Guolai Yang, Quanzhao Sun

C. Li, G. Yang, Q. Yu, and Q. Sun, “Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure,” Journal of Vibroengineering, Vol. 23, No. 5, pp. 1129–1137, Mar. 2021, https://doi.org/10.21595/jve.2021.21867

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.21867
UR  - https://doi.org/10.21595/jve.2021.21867
TI  - Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure
T2  - Journal of Vibroengineering
AU  - Yang, Guolai
AU  - Li, Cong
AU  - Yu, Qingbo
AU  - Sun, Quanzhao
PY  - 2021
DA  - 2021/03/31
PB  - JVE International Ltd.
SP  - 1129-1137
IS  - 5
VL  - 23
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Yang_2021,
	doi = {10.21595/jve.2021.21867},
	url = {https://doi.org/10.21595/jve.2021.21867},
	year = 2021,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	number = {5},
	pages = {1129--1137},
	author = {Guolai Yang and Cong Li and Qingbo Yu and Quanzhao Sun},
	title = {Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]G. Yang, C. Li, Q. Yu, and Q. Sun, “Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure,” Journal of Vibroengineering, vol. 23, no. 5, pp. 1129–1137, Mar. 2021, doi: 10.21595/jve.2021.21867.

Copy IEEE

Copied to clipboard!

Yang, Guolai, Cong Li, Qingbo Yu, and Quanzhao Sun. “Analysis of Projectile-Barrel Coupling Vibration Characteristics Considering the Radial Effect of Propellant Gas Pressure.” Journal of Vibroengineering 23, no. 5 (March 31, 2021): 1129–37. https://doi.org/10.21595/jve.2021.21867.

Copy Chicago

Copied to clipboard!

Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure

Abstract

Highlights

1. Introduction

2. Projectile-barrel coupling dynamic model

2.1. Load analysis of barrel

2.2. Finite element model

2.3. Simulation of physical field variation of interior ballistics

2.3.1. Simulation of propellant combustion process

2.3.2. Realize the loading of propellant gas effect

3. Analysis of numerical simulation results

3.1. Dynamic response process of barrel stress

3.2. Analysis of projectile motion in bore

3.3. Load analysis of cradle

3.4. Analysis of muzzle vibration response

4. Conclusions

References

Cited by

About this article

Related Articles