Self-organization and evolution in dynamic friction systems

1. Introduction

The synergetic paradigm of evolution and self-organization that was developed and widely used in the second half of the 20th century [1]-[3] has found its way into tribology as well [4]-[9]. It was established that the process of friction is described in terms of interconnected physical, physic-chemical and chemical phenomena that lead to various changes in the transition zone between two interacting surfaces. We will refer to this zone as tribosphere. If we follow the synergetic paradigm, then according to the principle of expansion of state-space dimension, first of all, it is necessary to describe the interactions between mechanical subsystems and the tribosphere [10]. Therefore, the forces that are formed on the surfaces in contact should be represented in the state coordinates of the system. The mathematical description of the forces in the state coordinates defines the properties of the link that connects interacting subsystems. It is important to note that the consideration of the contact interaction forces in the function of the state coordinates fundamentally changes the paradigm of friction analysis. Friction is already considered as a dynamic system in which the forces that depend on the coordinates of the state actually form an intra-system regulator [11]. Therefore, the parameters of this regulator, i.e., the dynamic coupling formed by the friction zone, determine the asymptotic stability of the tribosystem. When stability is lost in such a system, various attractors (limit cycles, invariant tori, and chaotic attractors) must form in the vicinity of the equilibrium. When studying tribosystems, we gave priority to the analysis of self-oscillations [10]-[19]. In recent years, several studies have been published that consider the conditions for the appearance of tori and strange (chaotic) attractors [10], [19]. Various ways of self-excitation are considered, including those associated with the formation of a time-delay argument [20]. In recent years, particularly great interest has been paid to the study of the stability and properties of the attracting sets of deformation displacements in friction systems during cutting [21]-[28]. At the same time, it is shown that vibrations affect the wear rate of the contacted pairs [29]-[31]. It was the change in the vibration properties of the friction unit depending on the state of the tribo-medium that led to the development of the direction in tribo-technology, which con-sists in the creation of systems for vibration diagnostics of friction processes [30]-[33].

However, in all known works on the dynamics of the friction process the dynamic link formed by the process is deemed to be set and constant during the life of the system. In our opinion, the next phase of research should take into account the changes in representation of forces in the state coordinates through modeling how irreversible transformations in the zone of the contact between interacting surfaces influence the tribosphere properties. These irreversible transformations in particular cause evolutionary changes of the properties of the friction system leading to a dynamic reorganization of the system during its functioning.

We emphasize that the power of irreversible transformations stimulates changes in the parameters of the dynamic coupling over time, changes the dynamic properties of the contact and the output characteristics of the friction unit, for example, the wear rate of the contacting pairs. The purpose of the research presented in the article is experimental-mathematical modeling of evolutionary reorganization in a dynamic friction system. It is the study of the evolution of the properties of friction due to the phase trajectory of the power of irreversible transformations in the friction zone that fundamentally distinguishes the materials presented in the article from the known ones.

2. Generalized mathematical model of the evolutionary dynamic system of friction. Method of its analysis

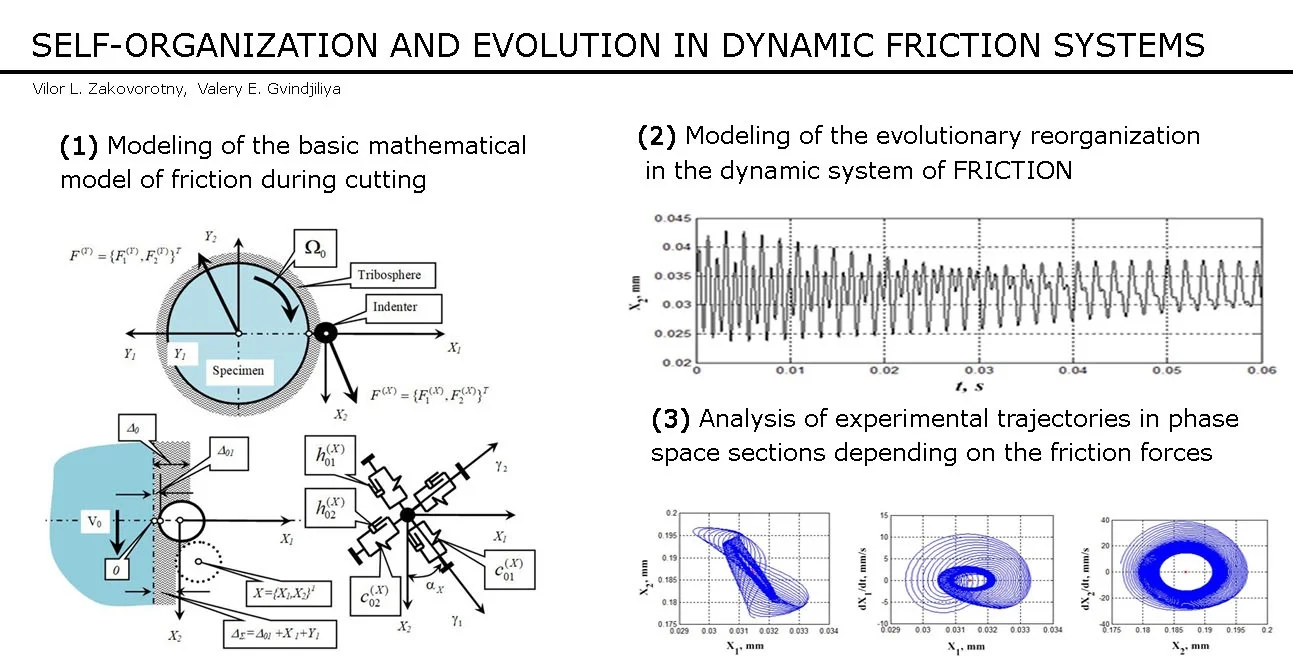
In the study of machine dynamics, it is usually represented in the form of a finite-dimensional space structure where separate generalized masses are linked with linear elastic dissipative connections [10], [14]. The principal properties of this system can be seen if we analyze systems with the following features (Fig. 1).

Deformational displacements $\mathbf{X}=\{X_1,X_2{\}}^T$ and $\mathbf{Y}=\{Y_1,Y_2{\}}^T$ of the two interacting subsystems are considered in a plane normal to the axis of rotation of the workpiece. 2. The object of the study is the contact between a spherical indenter of radius $r$ and a round specimen of radius $R$. Note that $R\gg r$. The specimen rotates at constant angular velocity ${\mathrm{\Omega }}_0$ represented in $\left[c^{-1}\right]$. 3. There are no torsional deformations of the specimen and the indenter. Therefore, generated forces of the contact interaction are applied to the centers of mass of the interacting subsystems and deformational displacements occur in the directions shown on Fig. 1. Here forces $F^{\left(X\right)}$ and $F^{\left(Y\right)}$ are equal and opposite. 4. Width ${\mathrm{\Lambda }}_0$ of the tribosphere can be considered constant and its properties - isotropic along the perimeter of rotation. 5. Forces that are formed at the contact of the surfaces depend on the depth of penetration into the tribosphere as well as on speeds of the relative movement of the surfaces.

Thus, forces are represented by dependence (Fig. 1):

where ${\mathbf{\Delta }}_{\mathrm{0,1}}$ is the preset value of the indenter without elastic deformational displacements; $V_0$ is relative sliding velocity without velocities of elastic deformational displacements; $p_1,...p_n$ are parameters included in the forces model. If Eq. (1) are defined, then the link that joins subsystems together into one dynamic system of friction is set. The above statements make it possible to define an equation for the friction system dynamics as follows:

where:

are matrices of inertia, of velocity, of other coefficients. That is why, if the reaction from the friction process of subsystem is not taken into account, $X$ and $Y$ are, first, asymptomatically stable and, second, autonomous. It is Eq. (1) that change the properties of the system and transform autonomous subsystems into a single dynamic system of friction. Currently existing dynamic models of the friction process differ in the ways Eq. (1) are presented [10], [14]. They are aimed at exposing various physical processes in the friction zone, for example, the decrease of friction forces as the speed of relative sliding increases [14]. At the same time, as a rule, scalar (not special) models of indenter oscillations are being considered. These models enable the explanation some issues with the loss of stability and appearance of auto-oscillations. Moreover, parameters of the model are deemed to be set and unchanging during the operation. Therefore, the most important question of the synergetic paradigm on the evolutionary reorganization is not examined at all. The basic concept of the evolutionary reorganization of the system means that the changes of tribosphere properties are associated with the phase trajectory of the power of irreversible transformations of input energy in the contact zone for the work done. Then, taking into account Eqs. (1) and (2) we obtain a dynamics evolutionary equation:

where $w_{i_i}(A-\varsigma )=\mathrm{e}\mathrm{x}\mathrm{p}[-(T_{i,1}{)}^{-1}(A-\varsigma )]+{\beta }_i\mathrm{e}\mathrm{x}\mathrm{p}[(A-\varsigma )\left(T_{i,2}{)}^{-1}\right]$ are kernels of integral operators, with that $T_{i.1}$, $T_{i.,2}$ are constant works with dimension $kgm$, these parameters describe the evolutionary heredity of trajectories as the work is done; ${\alpha }_i$ are parameters that determine the connection of the trajectory of power for the work done; $p_{0,i}$ is the initial parameter value. The system Eq. (3) properties are investigated in several stages.

At the first stage stationary evolutionary trajectory ($X_1^{*}\left(A\right)$, $X_2^{*}\left(A\right)$, $Y_1^{*}\left(A\right)$, $Y_2^{*}\left(A\right)$) is analyzed. It constitutes the solution to integral equation:

At the second stage we analyze the stability of trajectories ($X_1^{*}\left(A\right)$, $X_2^{*}\left(A\right)$, $Y_1^{*}\left(A\right)$, $Y_2^{*}\left(A\right)$) corresponding to parameters $p_1\left(A\right),...p_n\left(A\right)$. If they are stable, then they will be attractors for system Eq. (3). Otherwise, it will be necessary to analyze attractors in the neighborhood of the stationary evolutionary trajectory, their corresponding variations of contact interaction forces, changes of work and power of irreversible transformations as well as to adjust parameters of the dynamic link, that is to say the very stationary evolutionary trajectories. For this purpose, it is convenient to analyze in advance the properties of system Eq. (3) and to construct system bifurcation diagrams in the zone of identification of evolutionary parameters. However, even if there are no system bifurcations in the course of evolution, it is still possible to evaluate tribosphere properties from evolutionary diagrams of roots of the characteristic polynomial linearized in the neighborhood of the system equilibrium.

Earlier we have put this concept forward as a basis for constructing systems of dynamic diagnostics of the friction site state based on the use of autoregressive spectral analysis of the observed vibrational sequences [10], [34]-[36].

3. Example of the system and its properties

Let us examine system Eq. (3) where there are no deformations of the specimen present and let us take into account the following main features of modeling of forces in state coordinates [10], [14], [38].

1) The tribosphere exhibits gradient functional services [14], [38]. Therefore, as surfaces come closer, first, the forces of contact interaction increase and, second, normal and tangential forces are redistributed. Their thorough analysis shows that in certain cases there are potential barriers in these characteristics associated with various physical phenomena, for example, the destruction of the servovite film (protective tribofilm) [10], [37], [38]. Let us call changes in contact interaction forces caused by surfaces coming closer together approximation functions. If approximation functions are set, then for every gap we can obtain important characteristics of the friction site. For example, the ratio of tangential force to normal force in a given equilibrium point is usually interpreted as coefficient of friction. From the changes in the gap it is possible to establish force gradients that affect the existence condition of external friction, etc. In the dynamic system these gradients define the dynamic rigidity of the contact. In this paper we will only refer to the most common case where with the narrowing of the gap the forces are increasing steadily. The main properties of these functions can be described in rather simple expressions:

where $\rho$, $\upsilon$ are parameters having meaning of pressure and density respectively. They have dimensions [kg/mm²] and [kg/mm³]. $X_{\mathrm{0,1}}$ is the distance between the surface of the tribosphere and the apex of the indentor with the assumption that there are no elastic deformations.

Fig. 1Diagram of the basic model of the dynamic friction model

2) Research suggests that, firstly, contact interaction forces do not appear instantly. Secondly, there is some delay between variations of normal and tangential components of forces. Thirdly, when examining steady disturbed periodic motions phase shifts between variations of normal and tangential components of the forces are amplitude- and frequency-dependent [38], [39]. Finally, the trajectory covered by the indenter in relation to the specimen in the speed range (0.1-3.0) m/s remains practically unchanged once a new force balance is established. Therefore, the amount of delay depends on the relative sliding speed.

3) When the relative sliding speed is rising with the normal force unchanged the tangential component is decreasing which is associated with the temperature-speed factor. The above specific features allow the presentation of contact interaction forces in the following way:

where $T_1,\dots ,T_2$ are time constants that characterize the delayed transformation of elastic deformational displacement changes into forces; $k$ is a nondimensional parameter $k<1$; $а$ is a parameter that described the steepness of friction force decrease when relative sliding speed is increasing [s/m]. In Eq. (6) relation $T_1<T_2$ is fulfilled. And $T_1=l_1/V$; $T_2=l_2/V$ is true ($l_1$ is an efficient trajectory needed to establish the normal component and $l_2$ – the tangential component of forces). State coordinates in Eq. (6) have a limited range of definition $\left(V+\frac{d{X}_2}{dt}\right)>0$, $X_1<X_{\mathrm{0,1}}$. Nowadays the paper is published that takes into account delay of friction forces in depend on variation of deformational displacement, but in modeling of dynamic system the author used the model of pure time delay [20].

4. Equilibrium properties in the dynamic friction system

The system equilibrium is defined by conditions: $X_1^{}=X_1^{*}=const$, $X_2^{}=X_2^{*}=const$. From Eqs. (2) and (6) we obtain an equation for calculation of the equilibrium. If $X_{\mathrm{0,1}}=сonst$ and $V=const$ for $X_1^{*}$:

where ${\vartheta }_V=\upsilon [1-k\mathrm{e}\mathrm{x}\mathrm{p}(-aV\left)\right]$; $c_{\mathrm{\Sigma }}=[c_{\mathrm{1,1}}{c}_{\mathrm{2,2}}-(c_{\mathrm{1,2}}{)}^2\left]\right(c_{\mathrm{2,2}}{)}^{-1}$. After calculating $X_1^{*}$ we establish $X_2^{*}=\left\{\rho \right(X_{\mathrm{0,1}}-X_1^{*}{)}^2-c_{\mathrm{1,1}}{X}_1^{*}\left\}\right(c_{\mathrm{2,1}}{)}^{-1}$. Eq. (7) has three solutions. However, in the range of definition of the parameters it always has only one real solution because $\rho (X_{\mathrm{0,1}}-X_1^{*}{)}^2\gg {\vartheta }_V(X_{\mathrm{0,1}}-X_1^{*}{)}^3{c}_{\mathrm{2,1}}/c_{\mathrm{2,2}}$ and $X_{\mathrm{0,1}}>X_1^{*}$. Stability of the equilibrium is of fundamental importance. To analyze it is necessary to examine linearized equation in variations with respect to ($X_1^{*}$, $X_2^{*}$). After substitution of $X_1^{}=X_1^{*}+x_1\left(t\right)$ and $X_2^{}=X_2^{*}+x_2\left(t\right)$ from Eqs. (1) and (3) we obtain a linearized equation in variations:

where:

Since $X^{*}=\{X_1^{*},X_2^{*}\}=const$, then Eq. (8) has constant parameters. Then stability is defined with solutions of characteristic equation:

To achieve this the known criteria can be used [40]. To ascertain the mechanisms of stability loss in the system the structure of matrices $h^{\left(\mathrm{\Sigma }\right)}$ and $c^{\left(\mathrm{\Sigma }\right)}$ can be analyzed; they are not symmetric due to the reaction induced by the friction process [41]-[43]. They can be represented in the form of symmetric and skew-symmetric components $h^{\left(\mathrm{\Sigma }\right)}=h_C^{\left(\mathrm{\Sigma }\right)}+h_K^{\left(\mathrm{\Sigma }\right)}$ and $c^{\left(\mathrm{\Sigma }\right)}=c_C^{\left(\mathrm{\Sigma }\right)}+c_K^{\left(\mathrm{\Sigma }\right)}$. Therefore, due to the process reaction potential velocity and elastic links are formed (defined by matrices $h_C^{\left(\mathrm{\Sigma }\right)}$ and $c_C^{\left(\mathrm{\Sigma }\right)}$), as well as gyroscopic and circulatory forces (defined by matrices $h_K^{\left(\mathrm{\Sigma }\right)}$ and $c_K^{\left(\mathrm{\Sigma }\right)}$). If $h_C^{\left(\mathrm{\Sigma }\right)}$ is positively definite, then it is a dissipation matrix and given the positive definiteness of the symmetric part of the elasticity matrix the system has an asymptomatically stable equilibrium point. In the case when $h_C^{\left(\mathrm{\Sigma }\right)}$ is negatively definite, then it forms accelerating forces. Then the equilibrium point becomes unstable and gyroscopic forces cannot stabilize the equilibrium. Thus, the first main mechanism of the stability loss is determined by the transformation of the symmetric part of the speed coefficient matrix from positive definite to negative definite. Being positive definite matrix $c_C^{\left(\mathrm{\Sigma }\right)}$ forms forces directed towards the equilibrium; matrix $c_K^{\left(\mathrm{\Sigma }\right)}$ forms forces that are orthogonal to the direction of deformational displacements. They cause the formation of circular trajectories in relation to the equilibrium point. If the symmetric part becomes negative definite, then the system equilibrium becomes unstable and periodic variations start to develop in the system in the form of precession oscillations. The above statements complement and generalize the known studies in the field of the friction process stability. First, the system stability depends on control parameters $X_{\mathrm{0,1}}$ and $V$. Second, stability loss is crucially affected by delayed arguments $T_1$ and $T_2$ and parameter $a$ that influence matrix $h_C^{\left(\mathrm{\Sigma }\right)}$. Third, stability loss mechanisms can be examined only using a spatial model of the system. Gyroscopic and circulatory forces do not occur in scalar models.

5. Attractors that are formed in the neighborhood of the equilibrium

If the equilibrium is unstable, attractors form in its neighborhood [23]. The system builds a model of two interconnected oscillating circuits that have two main sources of self-excitation. One is caused by the delay in forces, the other is due to the existence of a region where the increase in speed corresponds to the decrease in the friction force. Therefore, three states can exist in the system: asymptomatically stable equilibrium point, asymptomatically stable limit cycle and two-dimensional invariant torus. Let us examine a system for which parameters of the indenter dynamic model are given in Table 1 and parameters of the dynamic link formed by the friction process – in Table 2. The system in question is steel-bronze. The bronze indenter is a sphere 8.0 mm in diameter. The specimen is made of steel. Friction with no lubricant. The methodology for parameter identification was detailed in the previous publications [13]-[15], [23].

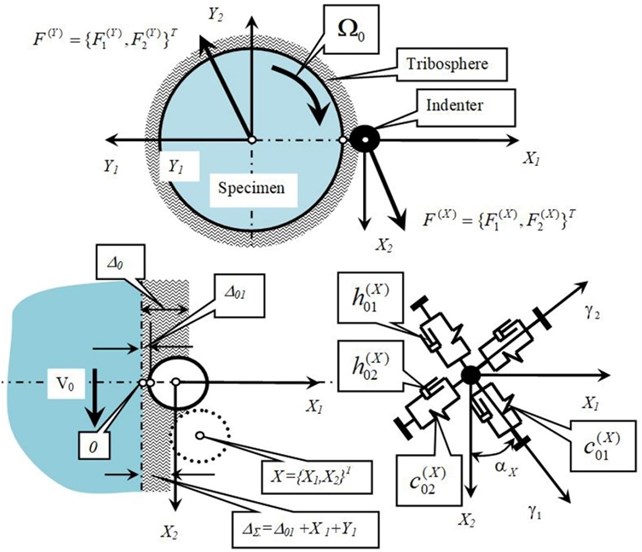
The range of definition of the indenter penetration into the tribosphere in the steady state is $\left(X_{\mathrm{0,1}}-X_1^{*}\right)\in \left(25;150\right)$mkm. The range of variation of dynamic rigidity of the contact at the site of definition of the indenter penetration into the tribosphere is $\partial F_1/\partial X_1\in \left(50;1200\right)$ kg/mm and $\partial F_2/\partial X_1\in \left(2.5;150\right)$kg/mm. As the surfaces get closer to each other, for these parameters the coefficient of friction increases from $k_{TP.}=$ 0.06 to $k_{TP.}=$ 0.18. Without going into too much detail, let us analyze the bifurcation diagram in the plane of these parameters (Fig. 2). The shaded area on Fig. 2 corresponds to an asymptomatically stable equilibrium, the hatched area “D-О-E” is where a two-dimensional invariant torus is formed. D-partition areas are also shown. They divide the parameter space into “В-О-С”, “С-О-F”, “F-O-A” areas and a shaded area. They differ in the number of roots of the characteristic polynomial of linearized equations in the right complex semiplane. In areas “В-О-С” and “F-O-A” there is one pair of complex conjugate roots with positive real roots, area “С-О-F” has two pairs of such roots. However, the boundaries within which the two-dimensional torus is formed are displaced on the bifurcation diagram (Fig. 2). Line “С-О-F” transforms into line “D-O-E”. Time charts for this case are shown in Fig. 3. It can be clearly seen that there is some pulling of high frequency oscillations towards low frequency ones.

Fig. 2Bifurcation diagram in plane (ρ,υ): “B-О-D” is an area of the orbitally asymptomatically stable limit cycle at high frequency; “E-О-A” is an area of the forming of the orbitally asymptomatically stable limit cycle at low frequency

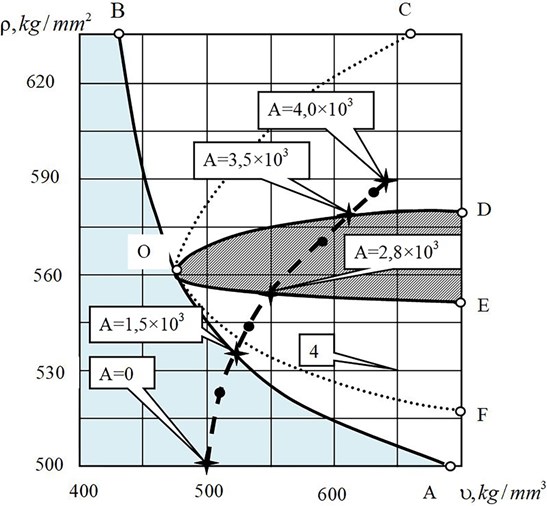
The variation of parameters of matrix $c$ results in shifting of roots of the characteristic polynomial Eq. (9). The roots can get closer to each other. In this case the area where the two-dimensional torus is formed degenerates.

Fig. 3An example of transformation of a two-frequency process into a single-frequency process

6. Reorganization of the dynamic system in the process of evolution.

Since there are no deformations of the specimen in the studies example, then taking into account Eqs. (3) and (6) it is necessary to use the system:

where $p_1=\rho \left(A\right)$, $p_2=\upsilon \left(A\right)$, $p_3=T_1\left(A\right)$,$p_4=T_2\left(A\right)$, $p_5=k\left(A\right)$,$p_6=a\left(A\right)$. System Eq. (10) is written for area $X_{\mathrm{0,1}}>X_1$. Let us give an example of the evolutionary reorganization of the system, parameters of which are specified in Tables 1 and 2. Parameters of kernels of integral operators for a relative sliding speed of 0.5 m/s are shown in Table 3.

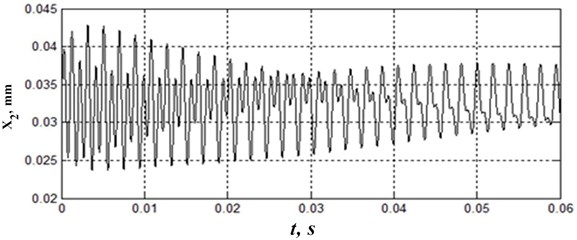
Fig. 4 shows examples of trajectories of elastic deformational displacements in plane $X_1^{}$, $X_2^{}$ in variations in relation to equilibrium points (trajectories on the left) as well as projections of phase trajectories in plane $X_1^{}$, $d{X}_1^{}/dt$ (trajectories in the middle) and $X_2^{}$, $d{X}_2^{}/dt$ (trajectories on the right). The bifurcation diagram (Fig. 2) shows values of work (black circles) for which trajectories are calculated in Fig. 4. The bifurcation diagram and examples of trajectory changes in the space of elastic deformational displacements demonstrate a large variety of formed attractors that change as friction forces do work. At the same time, as the work is done, certain regions stand out where the topology of the phase space remains unchanged, along with bifurcation points where topology changes. It should be emphasis that the transformation of topology of the phase space of the deformational displacements as a consequence of changes in the interactions of contacted surfaces, changes such properties of the contact as the power of irreversible transformations of the energy introduced into the contact. Therefore, for example, such parameters as wear intensity (increment of wear along the path), transformation of surface roughness, including the formation of equilibrium roughness, etc., do not remain unchanged after bifurcation points in the process of system evolution. These properties affecting the functional suitability of friction pairs during operation can change fundamentally depending on the parameters of the interacting subsystems.

Fig. 4Examples of trajectories in phase space sections depending on the work done by friction forces

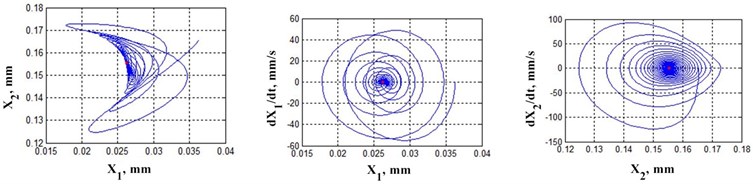
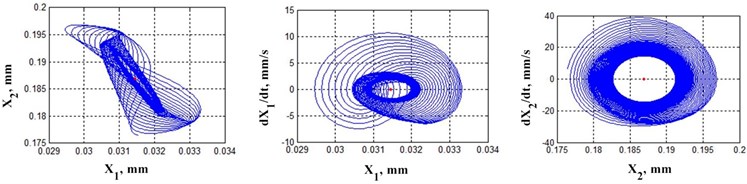
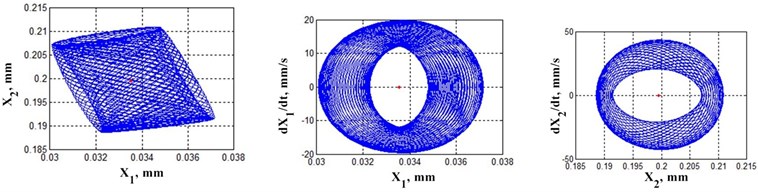
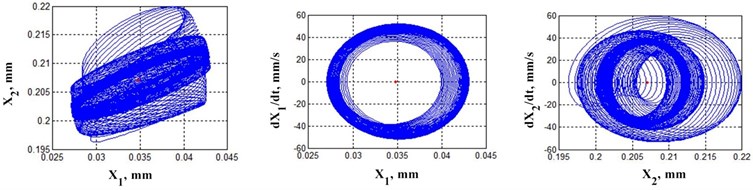
Presented in the article materials allow explaining the experimental investigations carried out during the last thirty years in the direction of evolution of the dynamic friction system. They are described in detail in monographs [10], [14], [36], [38] and articles [15], [22], [29], [30]. Let us briefly consider the results of the experimental study of the vibration characteristics of contacting pairs during the development of their wear. For concreteness, two systems: steel-brass and steel-glycerin-brass are considered. The vibrations in the contact interaction force space and the power of irreversible transformations as wear develops were studied. Vibrations were measured with vibration accelerometers, with subsequent integration and elimination of the trend due to uncertainty in initial conditions. The obtained vibration sequences in the form of vibration displacements, velocities and accelerations made it possible to reconstruct the vibration characteristics, their frequency images in the form of auto and mutual spectra as well as in the form of evolution diagrams of root distribution of the characteristic polynomial of autoregressive models of dynamics. Traditional statistical functional analyses of time sequences, as well as sequences based on the Poincare stroboscopic mapping algorithms, have been used in the analysis of oscillations. The following properties were found:

a) as wear progresses, there is a restructuring of the vibrational displacement attractors and associated contact interaction forces, including bifurcations of the attraction sets of deformations;

b) as a rule, there is a critical wear after which chaotic oscillations develop in the system. It is established that the general tendency of evolution of tribosystem from determinism at the initial stage to chaos occurs after some critical work of friction forces;

c) evolution and moments of bifurcations depend on initial parameters of the system, for example, on elements of a matrix of rigidity of indenter suspensions;

d) the intensity of wear depends on the evolution of dynamic contact properties and it can change fundamentally after bifurcation points;

e) in the same external friction conditions, but when changing, for example, the elements of the indenter subsystem stiffness matrix, selective transfer in the steel-glycerin-brass system may or may not be formed. Experiments show great sensitivity of selective transfer formation to small variations in friction system parameters as well as to small perturbations such as rotating spindle run-out.

We can continue the list of evidence showing the dependence of the output properties of the friction unit on the dynamic characteristics of the friction unit, and it is well known that these properties change in the course of functioning of the friction unit. All previously considered mathematical models of friction process dynamics, were “frozen”. They considered individual aspects of the dynamics, for example, the formation of attracting sets of deformations of the type of limit cycles [14], [15]. They did not allow us to analyze the evolution of the dynamical system, to consider bifurcations of the attracting sets of strain displacements formed during friction as the work is performed by friction forces. Finally, the friction process was considered without emphasis on its systematic character, including the internal connection of the power of irreversible energy transformations, the intensity of wear of contacting surfaces, the transformation of their geometrical topology, etc. But it is the consideration of the system, not the process, the functional connectivity of the system coordinates, their evolution, that are the main distinctive features of the proposed methodology and mathematical modeling, which analytically explain the above mentioned experimentally observed properties of friction units.

Our studies aimed at forming wear-free friction conditions have shown that the selective transfer may not be formed in friction of steel-bronze in glycerol in depend on the dynamic parameters of the indenter [37], [38]. There is other, as a rule, experimental studies aimed at revealing the connection of dynamics and wear resistance of friction units [15]-[19]. In this case at studying of output properties of friction, for example, wear resistance of contacting pairs, there is a fundamental problem of sensitivity of output properties of friction process to variations of dynamic parameters of interacting subsystems. Therefore, by analogy with dynamic systems, it is possible to introduce the concept of robustness on the output properties of the friction system.

The system approaches, the disclosure of functional relationships between coordinates provide an analytical and semantic basis for dynamic monitoring of the state of friction units [10], [21], [32-34]. The developed mathematical toolkit and researches of evolution of attractive sets of deformation displacements allow defining reliable information models of diagnostics of knots of a friction knowingly on the basis of mathematical modeling. For example, our analytical and experimental studies have shown that chaotic dynamics always develops in the dynamic system when tool wear approaches its critical value. The dynamic monitoring systems for rotary tribosystems developed on this basis have been implemented at a number of enterprises in Russia. Thus, the developed technique of mathematical modeling of evolution of friction system is a way of estimation of evolutionary transformations of dynamic system of a friction depending on naturally formed phase trajectory of power of irreversible transformations in the friction knot on the produced work.

7. Conclusions

The performed studies allow us to draw a general conclusion about the system-synergetic properties of the dynamic friction system. The representation of the forces formed in the interface area of the contacting surfaces in the state coordinates leads to the fact that these forces form an internal feedback and begin to play the role of an internal state regulator. Since the force model is nonlinear, such effects as branching of equilibrium points are possible in the system depending on the parameters. It is shown that in the vicinity of these points it is possible to form all the attractive sets known in nonlinear dynamics (limit cycles, invariant tori, chaotic attractors). Since the parameters of the system depend on the power of irreversible energy transformations in the friction zone, during the operation of the friction process, its dynamic restructuring is observed, which changes the output characteristics of friction and wear. It should be emphasized that the naturally released power of input energy in the contact area actually characterizes the factor not considered earlier, which changes the properties of the friction system. It is considered not “frozen”, but evolutionary changing, and the "generator" of these changes is energy release in the friction zone. Depending on the parameters of interacting subsystems, evolutionary trajectories, including bifurcations of attractive sets of strain displacements and their corresponding forces, change the properties of the friction system. The accounting of these changes, the methodology of modeling and studying as a single system fundamentally distinguish the given results from the known ones in the field of friction dynamics. Let us list the following most important provisions that follow from the completed study.

The dynamic friction system is formed as a result of interaction between two mechanical subsystems through a dynamic link created in the zone of the contact of interacting surfaces. The dynamic link that represents a model of forces in the state coordinates of the system is nonlinear in relation to elastic deformational displacements and their speeds. Therefore, the dynamic system of friction can serve as an example of various effects in nonlinear dynamics.

While examining linearized equations in variations in relation to the equilibrium point of elastic deformational displacements, matrices of speed coefficients and elasticity become nonsymmetrical due to the reaction by the process of friction. Therefore, dissipative, acceleration, gyroscopic, potential and circulatory forces are created in the course of the friction process. The main mechanisms of equilibrium stability loss in the system are associated with the transformation of the symmetric part of the speed coefficient matrix from positive definite to negative definite as well as with a significant increase in circulatory forces in relation to their potential components. The formation of circulatory forces makes it possible to explain the always experimentally observed trajectories of periodic deformation displacements of the contacting pairs in the form of circular precessional oscillations.

The principal property of a dynamic friction system is the change in the parameters and properties of the dynamic coupling formed, depending on the phase trajectory of the power of irreversible energy trans-formations in the contact region according to the work performed. As a result, the dynamic friction system undergoes evolutionary changes in its properties during its operation. They manifest themselves in the branching of equilibrium points (fork-type bifurcations) and in the change in the topology of the phase space in the regions surrounding the equilibrium. These changes, depending on the bifurcation points of the deformation displacements and the corresponding forces and powers, cause changes in the physical interactions on the contact surfaces. Moreover, the areas of stationary states alternating with changes in the topology of the phase space lead to the formation of chaotic dynamics in the deformation displacements. Chaotic dynamics usually correspond to the stage of catastrophic wear and tear. Therefore, this opens possibilities for building systems to diagnose the tribosphere state from its vibration data, for example, using models of autoregressive spectral analysis. This method has been tested in diagnostics of bearing units in machines, as well as in machining of materials by cutting. In the latter case, due to the coordination of the trajectories of the machine's executive elements programmed by the CNC system with the evolutionary changes of the system, the possibility of reducing the reduced costs of manufacturing a batch of parts by 1.5-2.0 times is shown.

It is found that the evolutionary changes in the properties of the dynamic friction system are sensitive to the variations in the parameters and the perturbations that always occur. Therefore, firstly, the wear of the contacting pairs changes with variations in the system parameters, and secondly, it does not re-main unchanged at individual stages of evolution. Thus, the results of studying the wear resistance of the contacting pairs obtained on experimental stands can be transferred to a specific machine with great care. Moreover, we can introduce the concept of “roughness” of the system to the evolutionary changes in its properties.

The developed mathematical tools are based on the synergetic paradigm of analysis and synthesis, ac-cording to which the mathematical modeling of interacting subsystems is based on the representation of interactions in state coordinates. In this case, the interacting subsystems are transformed into a single interconnected dynamic system. Changes in the properties of the bond, for example, as a result of the release of energy to the contact area, cause a change in the entire system. The given material is limited by mechanical interactions represented by forces, and the coordinates of the state are considered in the form of spatial elastic deformation displacements. It should be taken into account that the release of energy in the contact zone causes many other physical interactions, for example, the power of irreversible transformations is a source of heat production. Then, as the coordinates of the state, it is necessary to consider the thermodynamic parameters and they cannot but affect the mechanical parameters. Thus, the further development of the ideas given in the article should be extended to the system physics of interactions: thermodynamics; tribochemistry, including the problems of selective transport; molecular interactions (adhesion, diffusion), etc.