Study on vibration characteristics of ship mining system under composite load

2.1. Overall system structure

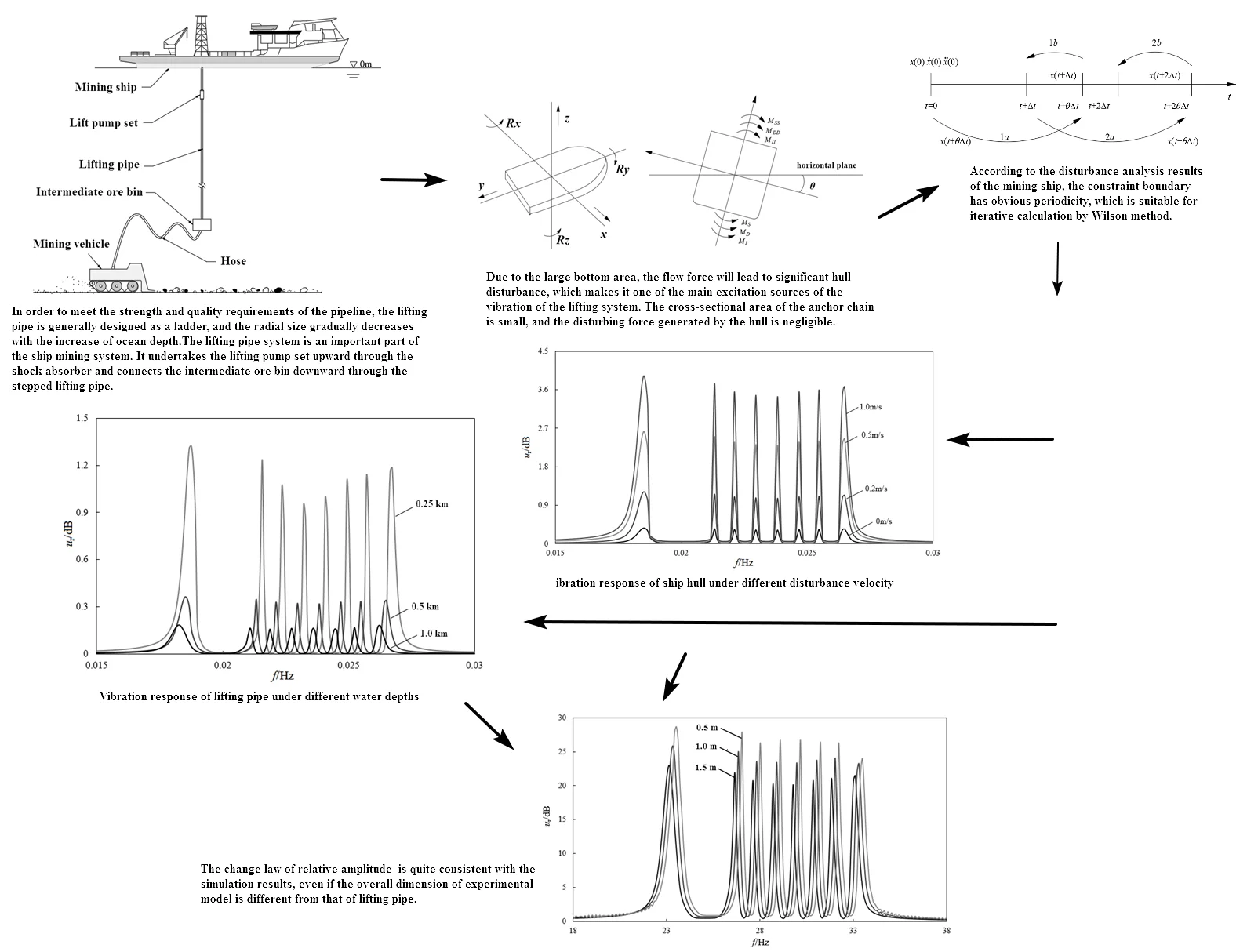
The mainstream ship mining system is mainly composed of mining ship, pipe lifting system, ore collection system and mining vehicle. Its cooperative working principle is shown in Fig. 1. This type of mining system has high flexibility and integration, high safety, scattered power sources [11], convenient equipment maintenance and good business prospects. However, during operation, due to the large length of the ore lifting pipe, vibration is easily produced under the action of ocean current, which brings great inconvenience to material lifting, ore bin storage and ship towing. In the whole deep-sea mining operation, the ore collection system is connected with the mining vehicle through a hose mechanism, and the ore is initially broken and decontaminated before entering the ore bin. In order to meet the strength and quality requirements of the pipeline, the lifting pipe is generally designed as a ladder, and the radial size gradually decreases with the increase of ocean depth.

Fig. 1Overall structure of ship mining system

2.2. Bearing analysis of lifting system

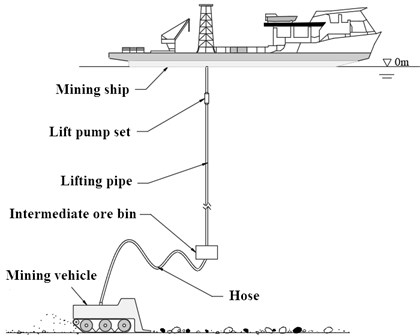
The lifting pipe system is an important part of the ship mining system. It undertakes the lifting pump set upward through the shock absorber and connects the intermediate ore bin downward through the stepped lifting pipe. The stress diagram of the lifting system is shown in Fig. 2. It can be seen that the action of ocean current is one of the key factors affecting the vibration of the lifting. Under the action of ocean current load $F\left(x\right)$, the node displacement response of lifting pipe is $u\left(t\right)$, and its radial and axial vibration components are $u_1\left(t\right)$ and $u_2\left(t\right)$ respectively.

In essence, ocean current refers to the large-scale transfer of seawater from one sea area to the other, which is a special current movement with obvious interaction effect with waves. According to the cause of formation [12], ocean current can be divided into wind current, density current and wave current, and nearshore current and offshore current according to different flow ranges. The speed and direction of ocean current movement is changing slowly with time and space. Therefore, in the actual ocean engineering calculation, ocean current is generally regarded as steady-state current [13]. The velocity of ocean current is different at different ocean depths. Through the test and exponential function fitting, it can be concluded that the functional relationship between the water flow rate $V_c$ within 5 km of the vertical deep sea and the sea depth $z$ under the condition of four-level wind load [14] is:

Fig. 2Bearing diagram of lifting system

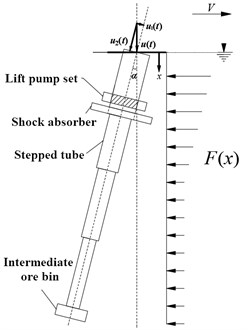
The curve between $V_c$ and $z$ can be drawn by MATLAB, as shown in Fig. 3. It can be seen that when the ocean depth exceeds 2 km, the water flow rate hardly changes and remains at about 0.1 m/s. The flow rate in the whole shallow water area (water depth 0-1 km) is greatly affected by water depth, and the flow rate at sea level is the largest, which decreases sharply with the increase of water depth. In moderate waters (water depth 1-2 km), the influence of water depth on water flow rate gradually weakens. The ocean current in shallow water has the most significant force on the lifting pipe system. According to the test, under the action of different wind loads, the changes of hydrodynamic load per unit area of lifting pipe in water depth of 0-1 km show significant consistency with the changes of water flow rate.

Fig. 3Relationship between current velocity and sea depth

2.3. Hull disturbance analysis

When the ship mining system works, the anchor chain can effectively restrict the displacement of the ship hull. However, due to the large bottom area, the flow force will lead to significant hull disturbance, which makes it one of the main excitation sources of the vibration of the lifting system. The cross-sectional area of the anchor chain is small, and the disturbing force generated by the hull is negligible. It is assumed that the center of gravity of the mining ship is located at the waterline, and the disturbance model is a six degree of freedom rigid body. In terms of vibration direction, set $x$ direction as transverse, $y$ direction as longitudinal and $z$ direction as vertical, as shown in Fig. 4. Taking the transverse plane vibration as the research object, set the active towing moment of the ocean current as $M_S$, the inertial towing moment as $M_I$, the damping towing moment as $M_D$, the active disturbance moment of the wave as $M_{SS}$, the inertial disturbance moment as $M_{II}$, the damping disturbance moment as $M_{DD}$, and the included angle between the hull and the horizontal plane as $\theta$. Then the governing equation of motion can be expressed as:

where $V_t$ is the displacement of mass the center, $h_a$ is the height of the transverse mass center.

The superposition of ocean current and wave determines the disturbance law of the hull, and the hull disturbance further affects the vibration of the lifting system. Based on the lateral sway mechanism and Newton's second law, the hull disturbance equation can be characterized as:

where $N_{\theta }$ is the disturbance damping coefficient, $I_{xx}$ is the moment of inertia, $J_{xx}$ is the additional moment of inertia, $a_{\theta }$ is the inclination of the superimposed force.

Fig. 4Hull disturbance model

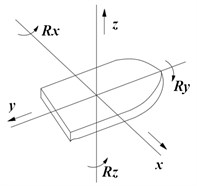
Fig. 5Variation of transverse included angle between hull and horizontal plane

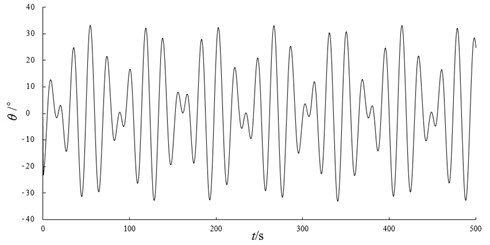
Under severe wind load conditions (extreme working condition, level 8 transverse wind load), the disturbance law can be analyzed according to the structural parameters, draft state and disturbance equation of the mining ship, as shown in Fig. 5. It can be seen that the hull disturbance has obvious periodicity, but the characteristic frequency is very low. At a specific ocean current rate, it is easy to cause resonant excitation force to the lifting pipe and significantly amplify the amplitude of the pipe.

3.1. Dynamic equation

The load of the lifting pipe system is complex and changeable. In addition to the composite flow load, the restrained end is also affected by the hull disturbance, which makes the lifting pipe have significant forced vibration in both transverse and longitudinal directions. The influence of different loads and constraints on vibration is expressed in the form of amplitude superposition [15], which is easy to cause damage and failure of the whole system, such as material blockage, pipe burst, overload deformation, etc., and reduce the working life of the lifting pipe. There are many factors affecting the composite load, such as wind load, ore bin storage, hull disturbance speed, lifting pipe length and so on. In the dynamic equation [16], these contributing factors can be expressed in the form of stiffness matrix and damping matrix. According to the bearing response diagram shown in Fig. 2 and the D’Alembert principle, the dynamic equation of the lifting system can be expressed as:

where [$M$], [$C$] and [$K$] represent the stiffness, damping and mass matrix of the lifting system, $F\left(t\right)$ is the composite load matrix.

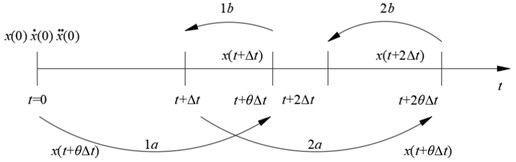
Due to the complexity and nonlinearity, it is difficult to get the dynamic equation of the lifting system by using the direct integration method. However, according to the disturbance analysis results of the mining ship, the constraint boundary has obvious periodicity, which is suitable for iterative calculation by Wilson method [17]. The principle of this calculation method is shown in Fig. 6. Firstly, the overall stiffness, mass and damping matrix are determined. Then, given the initial value, select the time step and calculate the integral constant to meet the requirements of unconditional stability. Finally, the equivalent stiffness matrix is formed, and the parameters such as displacement, velocity and acceleration at the next moment are calculated iteratively. This research method can obtain higher calculation efficiency and good convergence effect. The kinematic parameters can be solved by setting virtual positioning points through links RT real-time simulation software.

Fig. 6Solving principle of Wilson method

3.2. Vibration characteristics under different wind loads

According to Eq. (1), the wind load is converted to the ocean current rate. Taking the minimum disturbance of the mining ship as the boundary, the relationship curve between the relative amplitude $u_r$ and the excitation frequency $f$ of the lifting pipe at the water depth of 500 m under different wind loads can be calculated, as shown in Fig. 7. The formula for calculating the relative amplitude $u_r$ is:

where $a_n$ is the transient amplitude, $a_0$ is the reference amplitude at time 0, so as to ensure that the initial relative amplitude of the spectral response is 0.

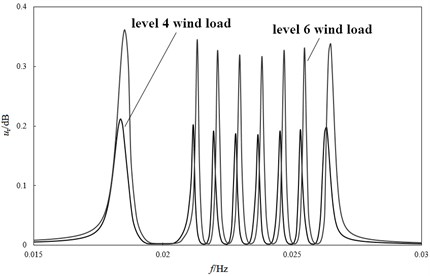
It can be seen from Fig. 7 that there are multiple characteristic frequencies in the range of 0.03 Hz for the lifting system, and the wind load has a certain impact on the characteristic frequency of the system. Under different resonance frequencies, the relative amplitude of specific wind load remains basically unchanged. At a specific resonance frequency, the relative amplitude under level 6 wind load is more than 50 % higher than that under level 4 wind load.

Fig. 7Vibration response of lifting pipe under different wind loads

3.3. Vibration characteristics of ship hull under different disturbance velocities

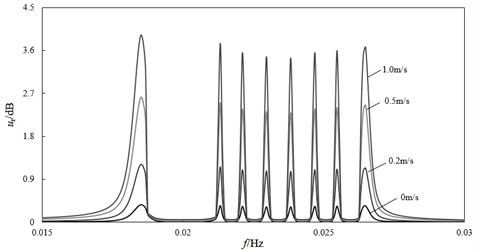
Hull disturbance is the result of the combined action of wind load and current. Under the condition of f level 4 wind load, the relationship curve between the relative amplitude and excitation frequency of the lifting pipe at the water depth of 500 m can be obtained, as shown in Fig. 8. It can be seen that the hull disturbance velocity has no effect on the characteristic frequency of the lifting pipe system, but the larger hull disturbance will cause the significant increase of the relative amplitude of the lifting pipe. Compared with wind load, the disturbance of mining ship has a more significant impact on the vibration of lifting system. When the ship mining system works, it is necessary to ensure that the mining ship is stably maintained in the effective resource area. However, there are often multiple mining areas in the whole project, and the installation and disassembly process of the lifting system is very cumbersome and time-consuming, which requires the mining ship to have great anti disturbance ability. It can be seen that strictly controlling the disturbance of mining ship through technical means is one of the most effective ways to reduce the vibration amplitude of lifting pipe, and it is also the key condition to ensure stable and efficient production.

Fig. 8Vibration response of ship hull under different disturbance velocity

3.4. Vibration characteristics of different water depths

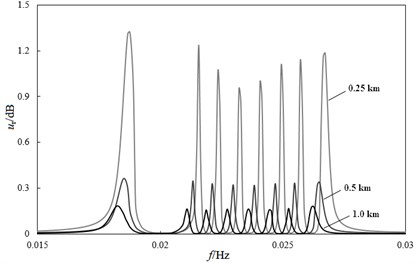
According to the bearing characteristics of the lifting pipe system, the ocean current under different water depths has different effects on the lifting pipe. Considering the mass change of ore lifting pipe, the vibration response results of ore lifting pipe under different water depths in shallow water can be calculated, as shown in Fig. 9. It can be seen that the characteristic frequencies of lifting pipe nodes at different water depths are different. With the increase of water depth, the characteristic frequencies show a decreasing trend. When the water depth is 250 m, the peak amplitude decreases first and then increases with the increase of excitation frequency. The ocean current load in the deep sea is weak, so the relative amplitude of the lifting pipe at the depth of 1 km is small. However, due to the continuity of the lifting pipe structure and large axial size, the overall deflection affected by the disturbance of the top hull is more significantly.

Fig. 9Vibration response of lifting pipe under different water depths

4.1. Design of test bench

In order to verify the vibration calculation results of the lifting system, according to the bearing characteristics of the lifting system, a vibration feedback test-bed of the lifting system is built based on the principles of analogy method and hammering method, as shown in Fig. 10.

Fig. 10Lifting system test bench

In the test bench, the lifting pipe is a stainless steel pipe with a length of 2 m, an outer diameter of 45 mm and an inner diameter of 42 mm. The immersion length of the tank after filling is 1.5 m. The waterproof YK – yd20 acceleration sensor is selected for vibration signal acquisition to measure the node vibration at 1 m and 1.5 m away from the steel pipe. The signal conditioning chassis adopts links – 01×01 series developed by Lingsi Chuangqi Company. It contains the voltage isolation conditioning module links – 02a01 at the acquisition end and the relay module links – 02d56 at the excitation end. The multi degree of freedom excitation is applied to the end of the steel pipe through the multi degree of freedom swing system, the periodic disturbance characteristics of the mining ship are simulated, and the connected actuator is controlled to apply hammering excitation.

4.2. Result analysis

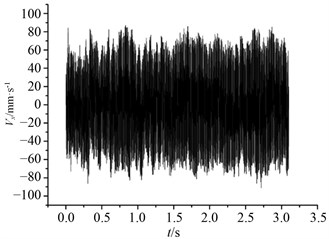
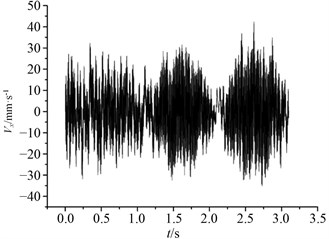
The variation curve of transverse ($x$-direction) vibration velocity signal $V_x$ of mine pipe model at 1 m node and 1.5 m node is shown in Fig. 11. It can be seen that compared with the 1.5 m node of the model, the vibration at 1m node is stronger, but the stability and periodicity of amplitude are more obvious. With the increase of water depth, the amplitude of vibration decreases significantly, and some discontinuities gradually appear.

Fig. 11Lateral vibration response of lifting pipe

a) 1 m position

b) 1.5 m position

Fig. 12Longitudinal vibration response of lifting pipe

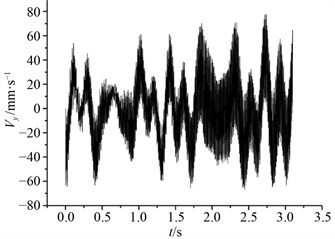
a) 1 m position

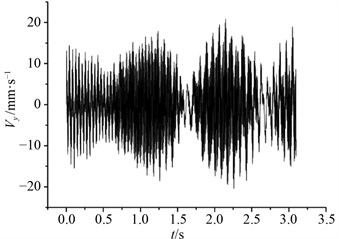
b) 1.5 m position

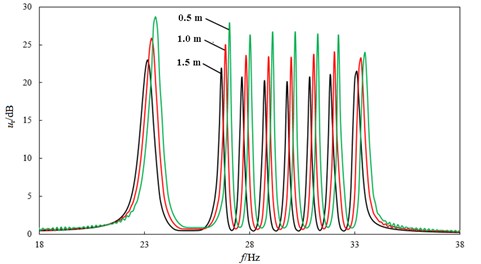
Fig. 13Spectrum response under different water depths

The variation curve of longitudinal ($y$-direction) vibration velocity signal $V_y$ of lifting pipe model at 1 m node and 1.5 m node is shown in Fig. 12. It can be seen that under the influence of hull disturbance constraints, at the same node position, although the amplitude peak of the longitudinal vibration of the riser model is slightly smaller than that of the transverse vibration, the fluctuation is more significant. The longitudinal vibration at the 1.5 m node also shows some discontinuous linearity.

Through Fourier transform and filter processing, the spectrum response under different water depths can be obtained in Fig. 13. It can be seen that the change law of relative amplitude $u_r$ is quite consistent with the simulation results, even if the overall dimension of experimental model is different from that of lifting pipe.