Six-DOF modular robotic arm bearing chatter suppression algorithm

3.1. Kinematic analysis of a six-DOF modular robotic arm

The study focuses on a modular robotic arm with six-DOF that has varied lengths of motion in each of its rotating joints. Different-sized modular joints are assigned in accordance with the function of power and load factors, taking into account the arm's range of motion. The first and fifth joint axes of the Six-DOFrobot arm used in the study are in the vertical direction, while the second, third, fourth, and sixth joint axes are in the horizontal direction. An axis-vertical linkage, an axis-parallel linkage, and six rotatable joints typically make up a Six-DOFrobot arm. These jointed bars are each joined to a maximum of two other jointed bars [15-16]. There are equivalent D-H representations for the various rotating joint coordinate systems due to the various properties of the particular axial joints. Table 1 lists the relevant D-H parameters.

As shown in Table 1, each rod $i$ can be represented by a scale representation where $i$ represents the angle between the two axis joint links and $i$ indicates the length of the rod, which is the shortest distance between the two joint axes (i.e. the torsion angle of the rod). By measuring the distance $d_i$ and the angle ${\theta }_i$ between the two rods, the study establishes the link between their positions. After adopting the normal D-H coordinate system’s parameters, the six-DOF robotic arm’s coordinate system is established. Equation must be satisfied by the built-in D-H parametric technique Eq. (1):

$T\left(z_{i-1},d_i\right)$ and $R\left(z_{i-1},{\theta }_i\right)$ in Eq. (1) stand for the rotation matrix around the axial joint and the translation matrix along the axial motion, respectively. The distance along the $z_{i-1}$ axis between $X_{i-1}$ and $X_i$ is indicated by the symbol $d_i$. ${\theta }_i$ indicates the rotation from $z_{i-1}$ to the corner between $X_i$ around the $z_{i-1}$ axis. $a_i$ stands for the separation between $z_{i-1}$ and $z_i$ along the $X_i$ axis. The angle of rotation from $z_{i-1}$ to $z_i$ is represented by ${\alpha }_i$, which denotes the orientation around the $X_i$-axis. Eq. (2) is then used to calculate the rotation and translation matrices’ expressions:

${}_i{}^{i-1}\mathrm{}T$ stands for the position transformation matrix in Eq. (2). By adding the D-H data to the equation, the transformation matrix between the individual axis joints is obtained. The transformation connection between the end of the robot arm and the base of the robot arm is the product of the transformation matrix between each neighbouring link, as shown in Eq. (3):

The transformation matrix between the coordinate system of the base of the robot arm and the matrix created by the combination of $n_{ij}$, $o_{ij}$, $a_{ij}$ in Eq. (3) can be calculated by multiplying the matrices. The end-effector of the robot arm's end-effector is represented by the three-dimensional coordinates ${\left[P_x,P_y,P_z\right]}^T$. The equations for the robotic arm’s forward motion can be determined using the D-H parametric technique, and if the rotation angle of the axis joint is known, it is possible to determine the position of the robotic arm end-effector with respect to the position of the coordinate system [17-18]. A kinematic model of the Six-DOFrobotic arm joint using the standard D-H parametric method is shown in Fig. 1.

Fig. 1D-H parameters modeling the joint movement of the robotic arm

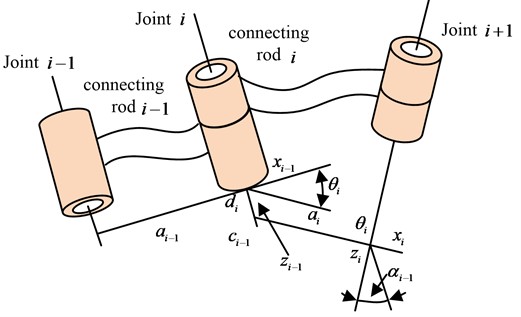
The inverse kinematics of the robot arm is generated and explained using the coordinates and velocity of the robot hand after deriving the forward kinematics of the robot arm and acquiring all the joint angles. Eq. (4) can be created by multiplying the left side of Eq. (3) by a factor of ${}_1{}^0\mathrm{}{T}^{-1}$ and the right side by a factor of ${}_6{}^5\mathrm{}{T}^{-1}$, using robot arm joint 1 as an example:

The inverse kinematic position transformation matrix is obtained by substituting the D-H parameters into equation; it is abbreviated and is displayed in Eq. (5):

The final expression for the corner of joint 1 is given in equation after Eq. (5)'s combination is solved for Eq. (6):

The expression for all joint angles can be produced in the same manner by applying the aforementioned equation, as demonstrated in Eq. (7):

where, $\alpha =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(g_{14}/g_{24}\right)$. The positive and negative kinematic equations for a Six-DOF robot arm can be calculated more precisely with all of the aforementioned equations. Moreover, the motion trajectory of each joint may be readily determined when the trajectory of the robot arm’s end effector is known. To operate the arm quickly, the robot arm control system is given efficient kinematic settings.

3.2. Design of a six-DOF robotic arm oscillation control method based on visual measurement and optimized PID

The end of a Six-DOFrobotic arm is subject to severe jitter during operation, so the research is based on a kinematic analysis of the Six-DOFrobotic arm, with displacement measurements of the vibrations at the end of the arm and thus active control of the changes. The study uses real-time tremor displacement signals obtained from visual measurements as control inputs [19-20]. The control algorithm is used to output a control voltage to achieve tremor suppression in the robotic arm. To complete the experiment, the study first selects the PID control algorithm in active control, incorporating intelligent optimisation strategies for parameter optimisation and selection. In accordance to the definition of the control algorithm, the corresponding controller is composed of three parts, namely Proportional, Integral and Differential. The relationship between the output and the input of the system is shown in Eq. (8):

where, $e\left(t\right)$ represents the input to the system and $u\left(t\right)$ represents the output of the system. $K_p$ represents the proportional parameter, $T_i$ represents the integral time parameter and ${\tau }_d$ represents the differential time parameter. $K_p$, $T_i$ and ${\tau }_d$ are all variables that can be regulated in the system. The transfer function of the system is shown in Eq. (9):

$G\left(s\right)$ stands for the system transfer function in Eq. (9). Fig. 2 displays a schematic diagram of the PID control method.

Fig. 2PID control and application principle

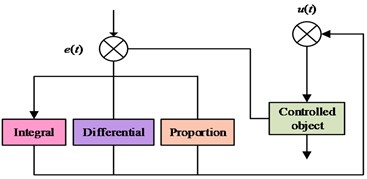
a) The PID control principle

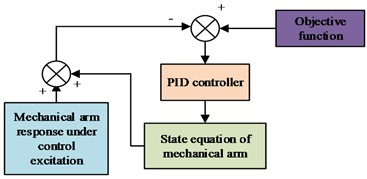
b) The application of PID control to manipulator

Fig. 2(a) is the PID control principle; Fig. 2(b) is the Application of PID Control to Manipulator. Due to the increased usage of control technology, research can be focused on the choice of objects in various systems. To obtain control of the system, control experiments can be performed by choosing just one or two of the three components: proportional, integral, and differential (i.e., P, PI, PD control), or by altering the settings of the various control connections. The selection of parameters affects the efficacy of the control, and depending on that selection, the researcher can choose the sort of approach. The control system is classified into two categories: online adaptive and ideal parameter determination [21]. The offline approach, also known as the rectification method, typically relies on artificial empirical equations to determine the parameters (usually using the Ziegler-Nichol response curve method). The step response of the controlled item can be used to determine the system model. Eq. (10) contains the model’s parameters and expression:

$G_p\left(s\right)$ stands for the system model in Eq. (10), $K_p$, $K_p$, and $T_d$ stand for the control parameters that were created by merging empirical equations. $\tau$ stands for the pure lag time, $\tau$ for the time constant, and $K$ for the model scale factor. The selection of the robotic arm end tremor data is then optimised using an intelligent optimization technique for visual measurement. The AFSA, an intelligent optimization technique based on a school of fish’s behaviour, is preferred. Fig. 3 depicts the algorithm’s implementation procedure.

The process begins by simulating the tremor at the end of the robotic arm as an artificial fish swimming. Assuming that the state at this point is $X$ and the corresponding sensing range is $Visual$, if a new position state $X_V$ is observed within the sensing range at a certain moment, the state of the position is discriminated to observe whether it is better than the current moment state. If it is better than the current state, it will continue to swim in the direction of the observation and get a distance of $Step$. If it is not better than the current state, it will continue to search for another position until it satisfies the requirement to end the iteration. The expression of the above process is given in Eq. (11):

$Rand\left(\right)$ stands for a function with values between [0, 1] in Eq. (11) while $Step$ stands for a movement step. Different states are denoted by $X$, which stands for $X=\left(x_1,x_2,\cdots ,x_n\right)$ and $X_V=\left(x_{v1},x_{v2},\cdots ,x_{vn}\right)$, respectively. The work integrates the artificial fish swarm method with the PID control algorithm to produce the best PID controller for the six-DOF modular robotic arm tremor control system. In the artificial fish swarm experiment, the PID parameters are utilised as simulation parameters, and the simulation control effect is employed as the nutrient concentration, i.e., the degree of adaptation. After numerous iterations of optimization, the ideal state results are obtained. Fig. 4 depicts the particular optimisation procedure and the functioning of the simulation control system.

Fig. 3Implementation process of the artificial fish algorithm

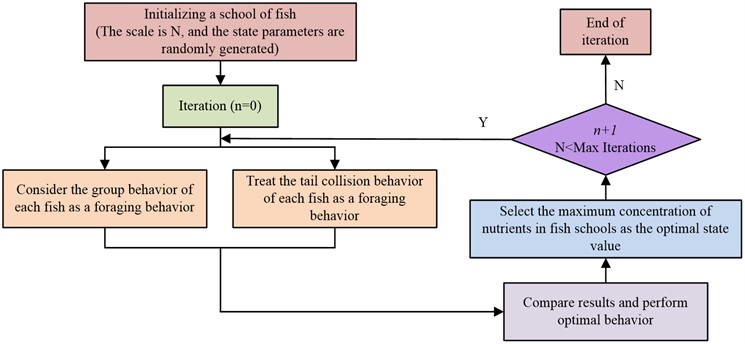
Fig. 4Control flow chart of fused artificial fish-PID technology

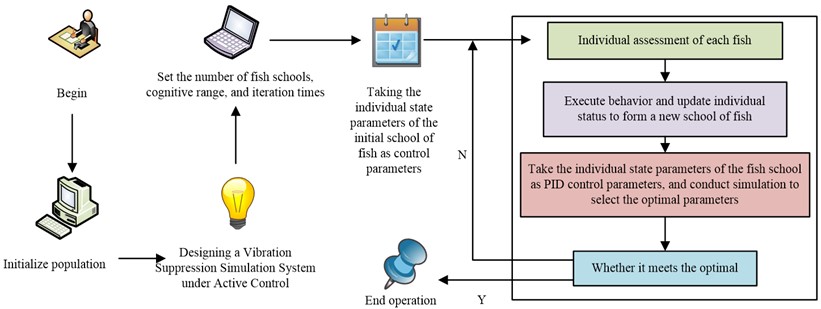
As shown in Fig. 4, the system typically includes a simulation model for a robotic arm, a PID controller, an objective function, and related parts. The general procedure is as follows: to induce a tremor response, the controlled item is exposed to the controller’s output. Where the controller receives feedback from the control error, which is the difference between the response function and the objective function, to create a closed loop. The Six-DOFrobot arm can be viewed as a cantilever in accordance with the structural model, which corresponds to the cantilever beam spatial state expression in Eq. (12):

In Eq. (12), $X$ represents the vibration displacement matrix, $u$ represents the input matrix, $K$, $M$, $C$ represents the modal stiffness, modal mass and modal damping of the mechanical arm cantilever beam and $\delta$ represents the force factor. Since the vibration control mode is the first stage mode, the stiffness, mass and damping of the first-order mode are assumed to be $K$, $M$, $C$, and the expressions of the relevant parameters need to satisfy Eq. (13):

where, $\zeta$ denotes the damping ratio and ${\omega }_n$ denotes the intrinsic frequency. And it can be noted that the equation of state of the robotic arm can be solved by using the structural damping ratio and the inherent frequency. The damping ratio and natural frequency can be extracted and solved using the frequency response method. The damping ratio solution is given in Eq. (14):

where, $f$ represents the frequency and this value has an effect on the magnitude of the output ratio. The final synthesis of the above gives the spatial equation of state of the robotic arm. The simulation test system is shown in Fig. 5.

Fig. 5Simulation system framework diagram

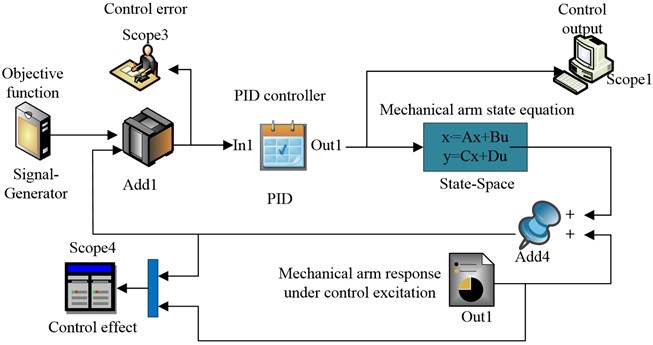
The spatial equation of state of the robotic arm in the simulation system of Fig. 6 has to be filled in according to the model equation, with $C$ taking the value range ${\left[\mathrm{1,0}\right]}^T$ and $D$ being substituted in as a zero matrix. In addition, as the control objective of the study is to suppress the tremor of the robotic arm, the objective function is set to 0. The simulation system platform is constructed according to the study control scheme.

4.1. Performance analysis of a Six-DOF robotic arm bearing chatter suppression system

In an effort to verify the effectiveness of the artificial fish swarm-PID control technique in a robotic arm-bearing tremor suppression system, the study began by testing the performance of the constructed system. The basic hardware environment setup for the experiments is presented in Table 1.

Firstly, Improved Ant Colony Algorithm (IACA) and Improved Convolutional Neural Networks (ICNN), which have the same experimental experience, were selected for performance comparison with the research algorithm. The number of iterations of each algorithm was set to 100 to ensure that the experiments were conducted in a fair and reasonable manner. The Cornell dataset and the Jacquard dataset were then selected to examine the performance metrics of the models, where the convergence variation of the algorithms is shown in Fig. 6.

Fig. 6Comparison of convergence changes for different algorithms

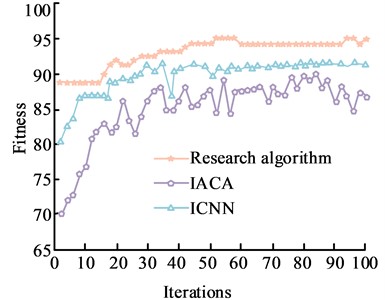
a) Cornell dataset

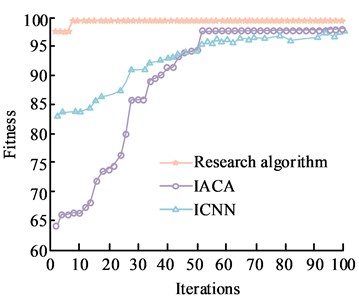
b) Jacquard data set

As can be noticed from Fig. 6, the values of the degree of adaptation under all three algorithm runs show a certain increase as the number of iterations increases. Fig. 6(a) shows the quiz of convergence on the Cornell dataset. With the iterations, the values of the degrees of adaptation of the two algorithms, IACA and ICNC, show a fluctuating trend of zigzag changes and do not have stable values. In contrast, the study algorithm has a maximum fitness value of 94 when the number of iterations is 60, which indicates a more stable convergence of the study algorithm. Fig. 6(b) shows the test of convergence on the Jacquard dataset, where the increase in the number of iterations causes the fitness values of the algorithms to change rapidly. When the number of iterations reaches about 9, the adaptation degree of the research algorithm reaches 99 and converges to 99. When the number of iterations reaches 52, IACA and ICNN have balanced adaptation degrees, but both are smaller than the research algorithm. The above results show that the research constructed algorithm has a better adaptation effect and a faster convergence rate. The Jacquard dataset was then used as the main dataset to test the extended performance. The accuracy and recall of the three algorithms were compared, and the PR curves are shown in Fig. 7.

Fig. 7PR curves of the cornell data set

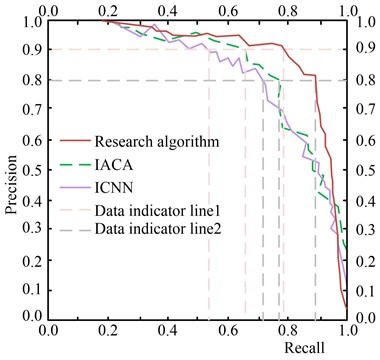
The PR curves in Fig. 7 show that when the precision rate of the algorithm is 0.8 and 0.9, the corresponding recall rates are 0.893 and 0.785, respectively. The above results indicate that the precision and recall values of ICNN and IACA are smaller for the same experimental conditions. This suggests that the proposed algorithm offers a more thorough service for the robotic arm vibration suppression system and has a higher accuracy rate in the optimisation selection of the system. The higher recall rate also improves the overall usage of the Six-DOFrobotic arm in the market. With this in mind, the study compares the mean absolute percentage error (MAPE) under different data sets tested, as shown in Fig. 8.

Fig. 8Mean absolute percent error contrasts across different data sets

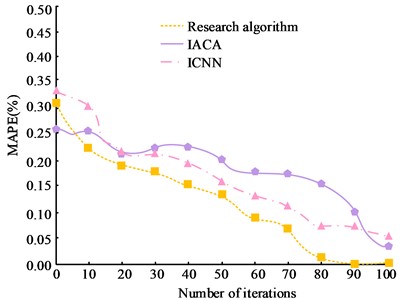
a) Cornell dataset

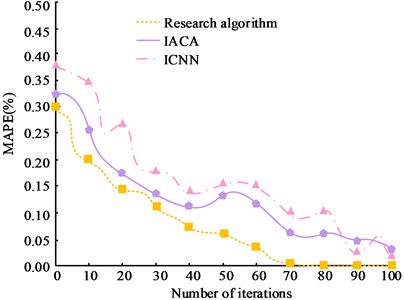
b) Jacquard data set

Fig. 8(a) is the test of MAPE on the Cornell dataset; Fig. 8(b) is the test of MAPE on the Jacquard dataset. From Fig. 8, it can be observed that as the number of iterations increases, the total MAPE values of all three algorithms on different data sets show a significant decreasing trend. Among them, the research algorithm has a lower MAPE value compared to the other three algorithms. In Fig. 8(a), the research algorithm has the smallest MAPE value when the number of iterations reaches 80, which is close to 0. The MAPE values of IACA and ICNN are 0.452 and 0.501 respectively, which are significantly larger than the research algorithm. In Fig. 8(b), when the MAPE value of the research algorithm is 0, the corresponding number of iterations is 70. The significant difference between the MAPE values of the research algorithm and the other algorithms can be seen on the basis of the significance results. This indicates that the algorithm proposed in the study has less error and better performance in the measurement of robotic arm tremor suppression.

4.2. Analysis of the practical application effect of the six degrees of freedom manipulator bearing chatter suppression strategy

The Six-DOF robotic arm tremor control system designed in the study is a control system under a PID controller. As the control implementation is piezoelectric sheet control, the output of the controller is the voltage acting on the piezoelectric sheet and the flexible arm model can be chosen as the spatial equation of state. The research design model shows that the intrinsic frequency, which can be determined using the frequency response method, and the structural damping ratio can both be used to solve the equation of state for the flexible mechanical arm rod. A swept output signal of 0.1 to 10 Hz is set in the signal generator for 10 s, and a sampling frequency of 90 Hz is selected for the vision measurement system. The data measurement is swept ahead of time to excite for a specific amount of time, while the acquired signal is analysed by digital signal processing. The results of the swept frequency excitation response and response spectrum are presented in Fig. 9 to verify that data is not lost.

Fig. 9Sweep excitation response and response spectrum results

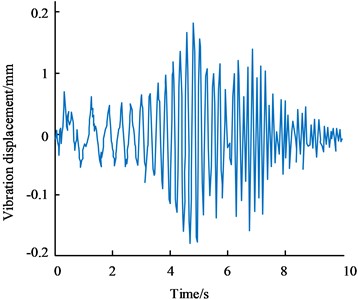
a) The frequency sweep excitation response

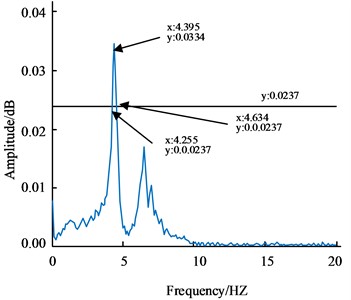
b) The response spectrum result

Fig. 9(a) is the frequency sweep excitation response; Fig. 9(b) is the response spectrum result. The data measurement is swept ahead of time to excite for a specific amount of time, while the acquired signal is analysed by digital signal processing. The results of the swept frequency excitation response and response spectrum are presented in Fig. 9 to verify that data is not lost. In Fig. 9(b), it can be seen that the peak frequency is $f=$ 4.395 HZ, so the inherent frequency is ${\omega }_n=2\pi f=$27.615 HZ. On the spectrum curve, make a straight line parallel to the $x$-axis with a height of $1/\sqrt{2}$ of the peak, i.e. 0.0237. The intersection of the straight line and the spectrum curve is the half-power point, i.e. (4.255, 0.0237) and (4.634, 0.0237), corresponding to frequencies of $f_1=$ 4.255 HZ and $f_2=$ 4.634 HZ. The damping ratio is estimated to be $\xi =(f_2-f_1)/2f=$ 0.0431 according to the half power bandwidth method. $\delta$ in $\delta M^{-1}$ of the equation of state is the force factor, which affects the output ratio. To obtain its value and verify the accuracy of the equation of state, the simulated equation of state response and the actual experimental response under the same excitation are compared and calculated to determine the output ratio. Using the above excitation experimental setup, the signal generator outputs a sinusoidal signal with a frequency of 4.395 Hz, which is amplified by the signal amplifier to a peak value of 40 V. The results are compared with a sinusoidal signal with a frequency of 4.395 Hz and a peak value of 40 in Simulink as input to obtain the equation of state response and adjust the spatial equation of state parameters. When $\delta M^{-1}$ is 0.27, the equation response is the same as the measured result. The final corresponding spatial equation of state is obtained as $X=\left[\begin{array}{ll}0& 0\\ -762.59& -2.3804\end{array}\right]X+\left[\begin{array}{l}0\\ 0.27\end{array}\right]u$. In addition to this, the study selected the Z-N method for determining the parameters of the PID control technique and applied it together with the research algorithm to the Six-DOFrobotic arm control system, the results of which are shown in Fig. 10 for comparison.

Fig. 10Comparison of the control results under the different algorithms

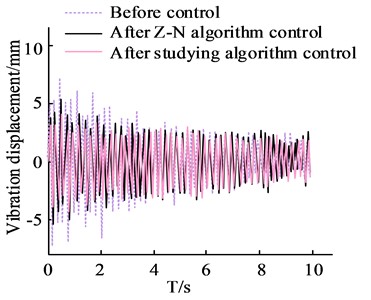
a) Comparison results of vibration displacement before and after control

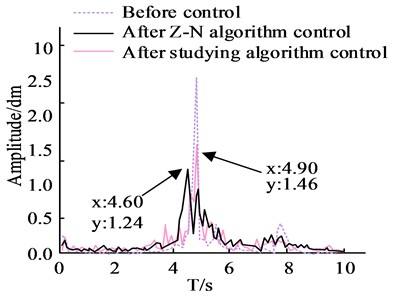
b) Spectrum comparison results before and after control

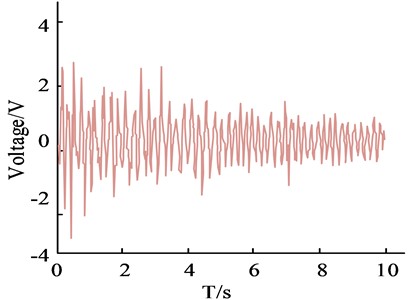
c) PID control output under Z-N method parameters

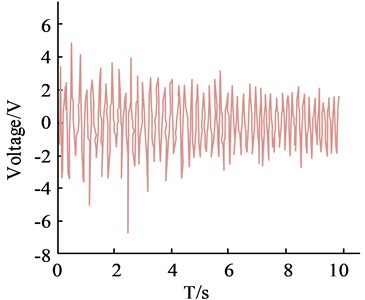
d) Study PID control output under algorithm parameters

Fig. 10(a) is the comparison results of vibration displacement before and after control; Fig. 10(b) is Spectrum comparison results before and after control; Fig. 10(c) is the PID control output under Z-N method parameters; Fig. 10(d) is the Study PID control output under algorithm parameters. Examination of the results in Fig. 10 demonstrates that the settings produced by both algorithms may govern the suppression of tremor in the robot arm. The two algorithms offer a superior tremor suppression effect on the tremor during the robotic arm's commencing operation phase and have a more substantial control effect in the first few seconds, according to the control time domain. The average control effects of the Z-N technique and the fish swarm method were calculated using the results of the spectrum analysis as the average control effect, and were found to be 51.56 % and 42.96 %, respectively. It is evident that the controller operating under the artificial fish swarm optimised parameter methodology has a greater control output signal when compared to the controller operating under the parameters of the Z-N technique. The study's proposed algorithm has better control performance, which effectively verifies the algorithm's superiority and better chatter suppression impact, according to the spectrum results. The specific effect is depicted in Fig. 11 and is the result of testing and recording the six-DOF robotic arm end-genuine effector's tremor suppression effect.

Fig. 11Tremor inhibition effect at the end of the manipulator actuator

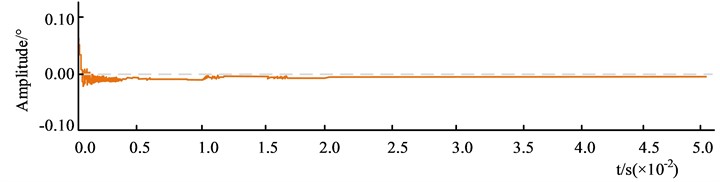
a) First experiment

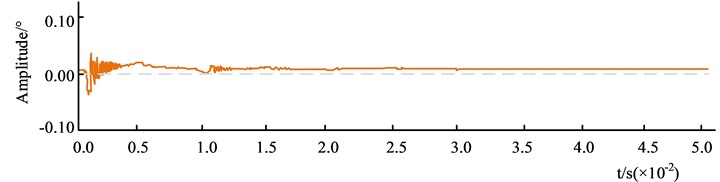
b) Second experiment

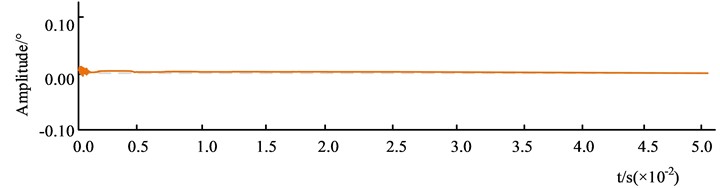
c) The third experiment

Fig. 11 shows the effect of tremor suppression on the robotic arm. The overall experiment was conducted three times, with the system running for 0.05 s. The "+" and "-" indicate the occurrence of rightward and leftward tremor movements of the robotic arm, respectively. Fig. 11(a) shows the first experiment. At the beginning of the experiment, the tremor amplitude of the arm decreased from 0.05° to 0.0001 s, and then trembled to the left, after which the tremor amplitude was more stable but always less than 0.00°. Fig. 11(b) shows the second experiment. At the beginning of the experiment, the amplitude of the arm tremor started to tremble rapidly from the right to the left and stabilized after 0.01 s, but the amplitude was always greater than 0.00°. Fig. 11(c) shows the third experiment. The robot arm tremor amplitude changes rapidly at the start of the experiment, tends to 0 at 0.0001 s, and remains stable thereafter. The data shows that the research algorithm has a high adaptability to robotic arm tremor suppression, and the amplitude gradually decreases with the number of experiments. The algorithm is able to converge to 0 quickly and can be applied to robotic arm tremor suppression.