Information exergy-based method for structural damage diagnosis

2.1. Generalized information entropy

Information entropy (Shannon entropy) was firstly proposed by C. E. Shannon as a criterion for analyzing and comparing probability distributions [11]. It provides a measure of information of any distribution and piece of information source.

It is now clear that the information entropy $S$ of an information source $E$ is related to the space division and the corresponding measurement defined on the space as the following form [13]:

where:

$A_i(i=\text{1},\text{2},\dots ),$ limited to $A_i\cap A_j=\varphi ,\forall i\ne j$ and $E=\underset{i}{\cup }{A}_i,$ is a division of the information source, like the realizations of a random variable;

$\mu (•),$ limited to $\sum _i\mu (•)=1,$ is the measurement of the information source on the dividing space, much like a probability density function.

Like Shannon entropy, generalized information entropy can work as a criterion for interpretating a piece of information source. In the case of damage diagnosis, it can reveal useful information about the condition monitoring time series, which is associated with the damage dynamics of the structure or system.

Generalized information entropy methods have been applied in mechanical and structural faults diagnosis using structural health monitoring information as information source and damage sensitive features as measures [12, 13]. Nevertheless these generalized entropy-based diagnostic methods are still based on moment sensory condition monitoring time series and uncertain diagnostic results may be resulted [14, 15]. Therefore the concept of information exergy is discussed in the following subsection.

2.2. Information exergy

Exergy is defined as the maximum theoretical useful work obtained if a system $S$ is brought into thermodynamic equilibrium with the environment by means of processes in which the $S$ interacts only with this environment [16]. Exergetic analysis has been used in [17] for chiller health monitoring and performance assessment.

Before introduction of the information exergy, definition of moment condition monitoring time series should be cleared. It refers to one piece of sensory time series quickly acquired at one moment. While in a condition monitoring process serval sets of condition monitoring time series are recorded.

Recently, information exergy based on the generalized information entropy has been coined for rotating machinery vibration faults diagnosis in [18].

Information exergy, denoted as $Y\left(t\right)$ is a time cumulating function of information entropy as follows:

where:

$S\left(t\right)$ is generalized information entropy of moment sensory condition monitoring time series at $t$;

$t_1$ and $t_{\text{2}}$ are the starting and ending moment of the condition monitoring process.

$Y\left(t\right)$ is called planar information exergy.

Planar information exergy $Y\left(t\right)$ is descreted as the following way to simplify the calculation and application:

where:

$S\left(i\right)$ is the generalized information entropy of sensory condition monitoring time series at descreted moment $i$;

$m(m=\text{1},\text{2},\dots ,M)$ is a discrete moment in the interval $[t_{\text{1}},t_{\text{2}}]$ and $M$ is the number of total descrete moments of the condition monitoring process.

Finally, all the $Y(m-1)$ are arranged into a vetor $\mathbf{Y}={[y_{\text{1}},y_{\text{2}},\dots ,y_{M-\text{1}}]}^{\text{T}}$ ($T$ is the transposition operator). This vetor combines all the information in a condition monitoring process, thus more confident diagnostic decision can be made.

3.1. Structural damage diagnostic method

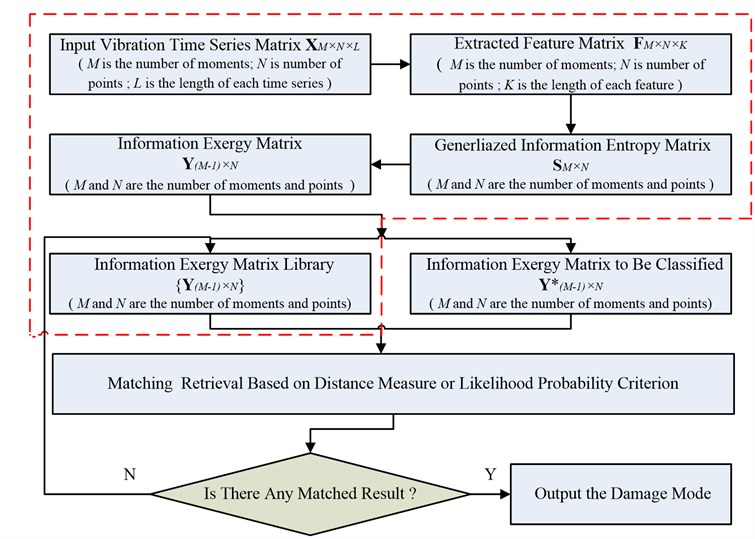
The proposed method for structural damage diagnosis (Fig. 1) primarily consists of two phases, the off-line learning phase (the part enclosed in the red dashed line) and the on-line exploiting phase as follows:

(1) Acquire vibrational signals through the data acquisition system, especially from the structural health monitoring system of the structure of interest.

(2) Extract features from the original vibration time series, such as singular value spectrum, wavelet packet decomposition power spectrum etc.

(3) Calculate the generalized information entropy pertaining to the extracted feature according to Eq. (1).

(4) Compute the information exergy related to the above information entropy with Eq. (3).

(5) Construct the information exergy library of typical damage modes of the interested structure which is to be used as a searching pool during the exploiting phase.

(6) Match retrieval based on similarity criterion (distance metrics or likelihood probability) when an unknown instance arrives.

(7) Make decision-whether to output matched damage mode(s), or to compile the unkown instance into the library as a typical damage mode itself.

Information exergy-based damage identification method is a generic framework that many kind of feature extraction techniques and similarity matching criterions can be embeded. Exergic features combining muti-moment condition monitoring time series can caputure the damage dynamics of the structure and reduce the uncertainty of the diagnostic results.

Fig. 1Flow chart of the structural damage diagnostic method based on information exergy

3.2. Extraction of singular value spectrum information exergy

Many kinds of information exergic features can be constructed to perform structural damage diagnosis. Here singular value spectrum information exergy is used to illustrate how information exergic features are extracted from the condition monitoring time series.

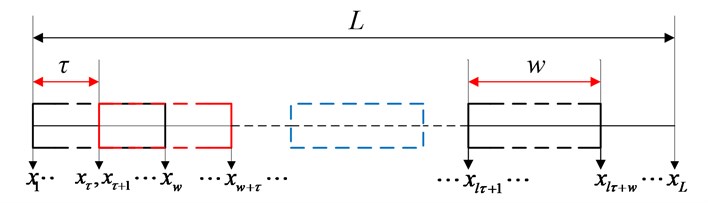
Firstly, the moment time series $x_n(n=1,\mathrm{}2,\dots ,L)\text{,}$ is embeded into the reconstructed phase space with an analysis window of width $w$ and time-delay $\tau$ (Fig. 2), thus its trajectory matrix is obtained as follows:

Note that when the time-delay $\tau$ equals unitary, then we get the Hankel matrix based trajectory matrices as in [19].

Then, the trajectory matrix $\mathbf{X}$ is subjected to singular value decomposition [20]:

and the diagnal matrix $\Lambda$ is as the following form:

None-zero ${\lambda }_i(i=\text{1},\text{2},\dots ,k)$ preserves principal information of the trajectory matrix and is defined as singular value spectrum of the original moment time series $x_n$.

Singular value spectrum can be viewed as a division of the original moment time series in the singular value spectrum space with the following measure:

Thus generalized information entropy can be difined according to Eq. (1) using $\mu \left({\lambda }_i\right)$. Hereafter this kind of generalized information entropy is denoted as singular value spectrum infomation entropy (SVS-InEn).

Fig. 2Illustration of the trajectory matrix construction schematic

To some exent, SVS-InEn reflects the complexity of energy distribution of the moment time series in the singular value spectrum space. The larger the SVS-InEn is, the more disperse the energy is and the more complicated the moment time series is.

Based on the above analysis, one SVS-InEn can be derived for each moment time series using Eq. (7) and Eq. (1). Considering Eq. (3), corresponding singular value spectrum information exergy is obtained by combining results of all the moment time series together, hereafter abbrivated as SVS-InEx.

Further taking the multi-points sensory information into account, a SVS-InEx feature matrix $\mathbf{Z}$ can be obtained arranging multi-moment and multi-point condition monitoring information in the row and column, respectively:

where $M$ and $N$ are the number of total discrete moments and sensory points of the condition monitoring process.

Other types of information exergic feature can be constructed in a similar procedure. The SVS-InEx feature matrix merging time and space information of a structure as damage sensitive index will be applied to the damage diagnosis of a truss-like structure in the following section.

4.1. Experimental setup

The structure (Fig. 3(a)) used in this study is a one by one bay three-story truss structure. It is composed of angle steel bolted together in the four vertices of each level and the dimension is 400 by 400 by 900 (in mm). To facilitate the management of the date files and damage scenarios, all the 16 vertices of the structure are marked as $i-j$ from the top to the bottom, where $i$ and $j$ are the level number and the vertices of each level, respectively. Each bolted point off-table is installed an acceleration sensor (Fig. 3(b)) to collect its vibrational time-series signal and total of 12 channel signals are acquired in every running. During the study, ES-15 hydraulic shaking table (Fig. 4) output a sine wave of 3 mm amplitude and 12 Hz frequency is employed in the experiment to excite the truss structure.

Fig. 3Three-story truss structure: a) overall view, b) details of the sensor installation

a)

b)

Fig. 4ES-15 hydraulic shaking table

4.2. Damage modes and data preparation

Three structural damage modes are considered in this case study and they are tabulated in Table 1. The structure was initially bolted by a dynamic wrench to work as benchmark undamaged condition. While bolt at the 1-2 point of the structure was loosed to simulate single bolt loosing damge mode 2 and both bolts at the 1-2 and 2-2 joint were released as multiple bolt loosness damge mode 3. During the tests, other factors that may have impacts on the diagnostic processes were tightly controlled to study potentials of the proposed information exergy-based method for damage identification.

During conditioning motoring process, four pieces of moment condition monitoring time series of acceleration signals were acquired. Each moment condition monitoring time series was sampled with a sampling frequency of 200 Hz and data points of 1 K with the Emerson 2130.

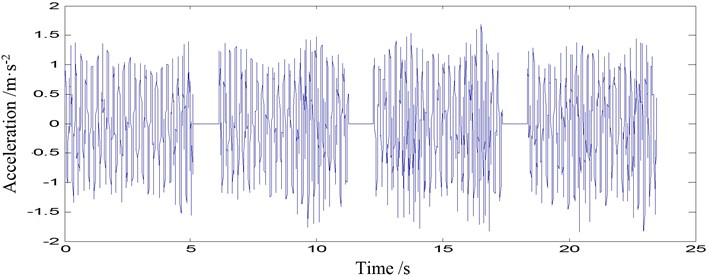
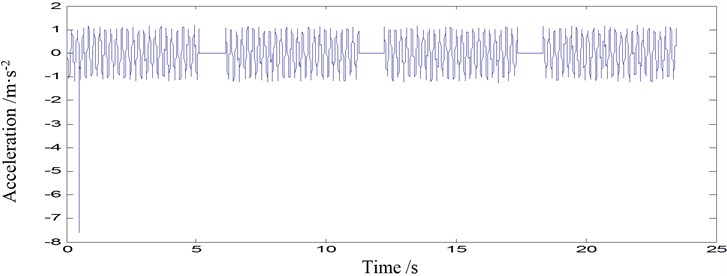
Fig. 5Acceleration time-histories of point 1-2 under three scenarios: a) damage mode 1, b) damage mode 2, c) damage mode 3

a)

b)

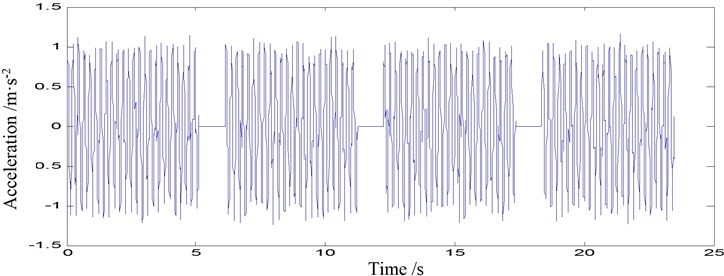
c)

4.3. Results and discussions

The acceleration signals of point 1-2 and point 2-2 under these three scenarios are illustrated in Fig. 5 and Fig. 6, respectively. For space reasons, the four pieces of time series of each scenario are plotted in the same subfigures with a spacing of 1 s (the corresponding flat parts).

Fig. 6Acceleration time-histories of point 2-2 under three scenarios: a) damage mode 1, b) damage mode 2, c) damage mode 3

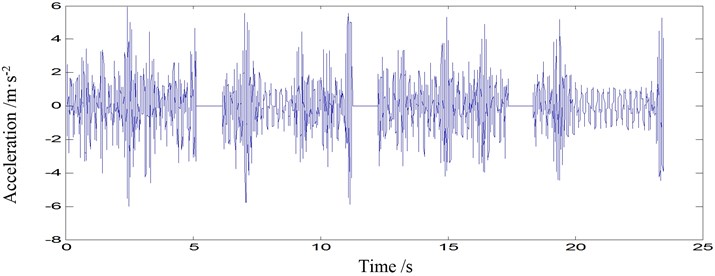
a)

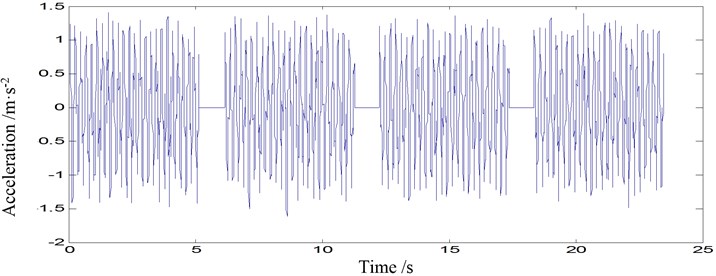
b)

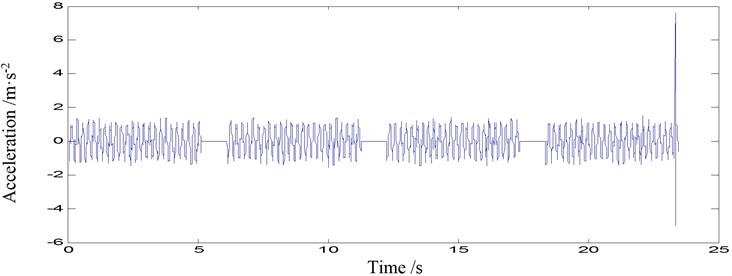
c)

It is noticed that the moment time series from the same damage modes aquired consecutively demonstrated very different patterns, such as Fig. 6(a). Also, there are outliers in one of the four samples (Fig. 5(b) and Fig. 6(c)). Damage diagnosis based on these moment time series will result in uncertain or even errorous results.

4.3.1. Qualitative results with discussions

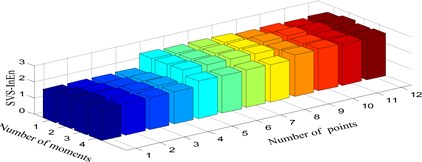
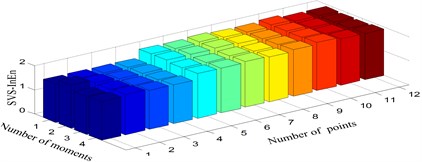
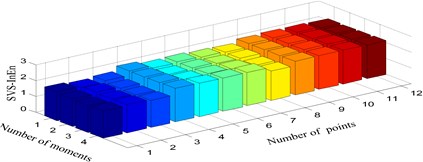
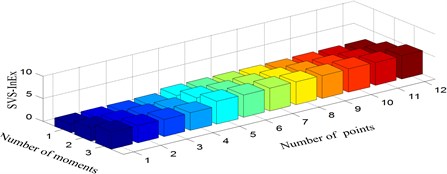
Four consecutive moment time series of the accleration of the chalked sensory points (Fig. 3) are employed for damage identification of each scenario. After data preprocesssing, the SVS-InEn and SVS-InEx features for the two bolt looseness damage modes are respectively shown in Fig. 7 and Fig. 8. Please note that the sensory pionts (1-1, 1-2, ..., 3-4, as marked in Fig. 3(a)) are sequentially denoted from 1 to 12.

Fig. 7Singular value spectrum information entropy under three scenarios: a) Damage mode 1, b) Damage mode 2, c) Damage mode 3

a)

b)

c)

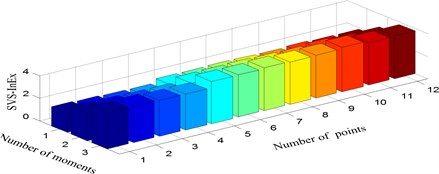
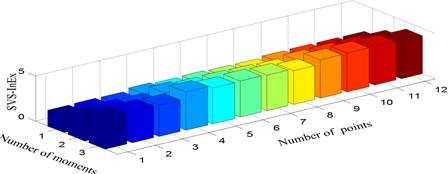
Fig. 8Singular value spectrum information exergy under three scenarios: a) damage mode 1, b) damage mode 2, c) damage mode 3

a)

b)

c)

Some results can be concluded from these two figures. Firstly, the SVS-InEn is inclined to decrease with the occurrence of bolt looseness and this is true as the less uncertainty one information source is the smaller the information entropy is. Secondly, although the SVS-InEn can differentiate damage mode 2 from damage mode 1, it can not identify the multiple bolt looseness (damage mode 3) from undamaged scenario (damage mode 1) with high confidence, because SVS-InEn of the two cases are both within almost the same range, i.e. 1~3 (Fig. 7). Thirdly, both the two damaged modes are regconized as different from the integrity mode by the SVS-InEx feature since SVS-InEx of the three senarios are varying within different ranges (Fig. 8). Finally, it is observed that the variance between damage mode 2 and damage mode 1 is much larger than that between damage mode 3 and damage mode 1, which is counter-intuition and needs further studies.

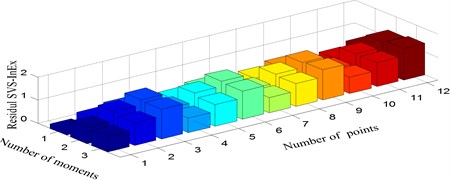
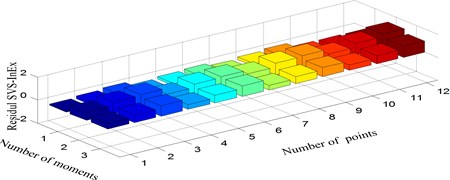
Fig. 9Residual singular value spectrum information exergy: a) damage mode 1 vs. 2, b) damage mode 1 vs. 3, c) damage mode 2 vs. 3

a)

b)

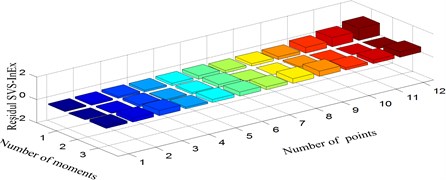
c)