Numerical investigation of dynamical properties of vibroactive pad during hot imprint process

1. Introduction

The exceptional potential of hot imprint technology like: low cost, easy implementation and ability to obtain high resolution are the main reasons for further investigation, establishment and application of such manufacturing capabilities. The basic principle of hot embossing composes from following major steps: first of all polymer substrate is heated above its glass transition temperature. Then a mold (or master) is pressed against the substrate. Lastly, the system is cooled down below glass transition temperature, and the embossed substrate is demolded from the tool. On the other hand there is necessity to study the risk of formed microstructure potential defects, which can occur as the result of material melting and releasing of the structure from the mold. These defects include material shrinkage, visible cracks, etc. One of the ways to improve the quality of replicas can be usage of high-frequency vibrations in the process of mechanical hot imprint. Ultrasonic vibrations [1-4] are widely applied in industrial processes, especially in welding and joining of thermoplastic with low softening temperature.

Ultrasonic vibrations during the process of hot imprint help diminish or completely avoid bubble defect in the pattern. It is also revealed that ultrasonic vibrations forced softened polymer to move to the center of the pattern area. The effect of ultrasonic vibrations asserts better under the action of lower contact force, because high contact force may inhibit amplitudes of ultrasonic vibration [5].

As it is revealed high frequency vibrations can be used as a measure to improve the quality of replicas [6], on the other hand it is necessary to know working regimes of the equipment, which generates such vibrations, in this case working regimes of vibroactive pad. To perform such an analysis experimentally is impossible, so it was decided in this paper to create model of vibroactive pad and analyze this pad using Comsol Multiphysics software (with and without the action of mechanical load) [7, 8]. Later on, the results of numerical analysis are compared with real construction (without mechanical load (since with load it would be impossible to observe vibration modes), when observing it with holographical inferferometer – PRISM).

2. Finite element model of vibroactive pad

Modeling of vibroactive pad used in hot imprint process as frequency generator is presented in this section.

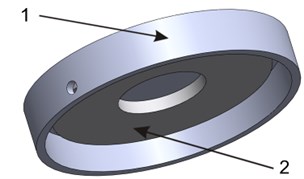
Aluminum cylinder with the top surface and a mounting hole in the side wall was chosen as a vibrating pad. The drawing of the vibrating pad with the mounted piezoelectric element is shown in the Fig. 1.

Fig. 1The 3D view of the pad (1) with the piezoelectric element (2)

The applicability of vibroactive pad vibration in the process of hot imprinting was analyzed numerically using finite element method. The dynamic parameters of the vibroactive pad (Fig. 1) were calculated using program COMSOL Multiphysics 3.5a. Dynamic research of vibroactive pad was carried out under different conditions: without mechanical load and with load in the center of vibroactive pad.

The geometrical parameters of vibroactive pad are: vibroactive pad thicknesses ($h_{Al}$) is 2 mm, thickness of piezo ceramic ring $h_{PZT}$ is 3 mm, and total height of the vibroactive pad $h$ is 10 mm. It is necessary to determine boundary conditions and initial value of the parameters of the model. Vibroactive pad’s bottom surface is fixed (Fig. 2). Potential difference $Q$ according to the experimental results between the upper and the lower piezoceramic ring surfaces vary from 5 to 150 V. The computational scheme of vibroactive pad is presented in Fig. 2.

Fig. 2Computational scheme of vibroactive pad (displacement (u, v, w), thickness of vibroactive pad (hAl), thickness of piezo ceramic ring (hPZT) and height of vibroactive pad (h))

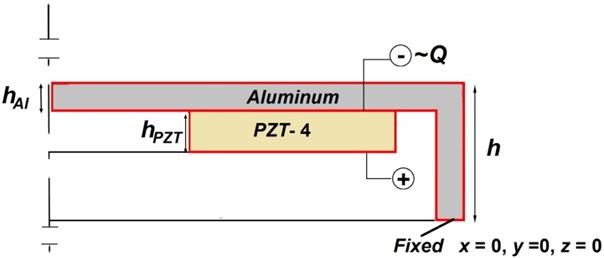
Fig. 3Tetrahedral finite element [9]

The pad’s material is aluminum (D16) and the disk is modeled as a piezo ceramic material PZT-4. The PZT-4 material’s and aluminum’s parameters were chosen from Comsol Multiphysics material library.

Quadratic tetrahedral finite element (which has ten nodes and four dependent variables in each node (displacements in $u$, $v$, $w$ directions and voltage $Q$)) was chosen for modeling (Fig. 3).

The material parameters for the piezoelectric material were specified according to: selecting the stress-charge form based on the constitutive equation and entering the material data (the elasticity-matrix elements in the $c_E$ matrix, the piezoelectric coupling-matrix elements in the e matrix, and the relative permittivity in the ${\epsilon }_{rS}$ matrix). The material properties in this model were set considering that the polarization is in the z direction, which is a common orientation, according to the literature.

Elasticity matrix: The elasticity matrix defines the stress-strain relation, and is denoted as matrix $c_E$:

where $\sigma$ is stress, and $\epsilon$ is strain,

$c_E=\left[\begin{array}{cccccc}1.38999e11& 7.78366e10& 7.42836e10& 0& 0& 0\\ 7.78366e10& 1.38999e10& 7.42836e10& 0& 0& 0\\ 7.42836e10& 7.42836e10& 1.15412e10& 0& 0& 0\\ 0& 0& 0& 2.5641e10& 0& 0\\ 0& 0& 0& 0& 2.5641e10& 0\\ 0& 0& 0& 0& 0& 3.0581e10\end{array}\right].$

Coupling matrix: The coupling matrix defines the piezo coupling matrix e, used in the stress-charge form of the constitutive equation:

where $\sigma$ is stress, $\epsilon$ – strain, and $E$ is the electric field,

$e=\left[\begin{array}{cccccc}0& 0& 0& 0& 12.7179& 0\\ 0& 0& 0& 12.7179& 0& 0\\ -5.20279& -5.20279& 15.0804& 0& 0& 0\end{array}\right].$

Relative permittivity: The relative permittivity ${\epsilon }_{rS}$ appears in the constitutive relation on stress-charge and strain-charge forms, respectively:

${\epsilon }_{rS}=\left[\begin{array}{ccc}762.5& 0& 0\\ 0& 762.5& 0\\ 0& 0& 663.2\end{array}\right]$.

Piezoelectric FEM equations can be written in terms of nodal displacement $\left\{U\right\}$ and nodal electrical potential $\left\{\phi \right\}$ for each node.

where $\left[K_{uu}\right]$ is mechanical stiffness matrix, $\left[K_{u\phi }\right]$ is piezoelectric coupling matrix, $\left[K_{\phi \phi }\right]$ is dielectric stiffness matrix, $\left[M_{uu}\right]$ is mass matrix, $\rho$ is piezoelectric density, $\left[N_u\right]$ is matrix of elemental shape functions, $\left[C_{uu}\right]$ is mechanical damping matrix, $\left[B_u\right]$, $\left[B_{\phi }\right]$ is derivatives of FEM shape functions, $\left[c\right]$ is elastic coefficients, $\left[e\right]$ is piezoelectric coefficients, $\left[\epsilon \right]$ is dielectric coefficients, $\beta$ is damping coefficient, $\left\{F\right\}$ is external mechanical effect and $\left\{Q\right\}$ is electrical effect.

The understanding of the resonance characteristics of vibroactive pad can be investigated by visualizing the displacement, generated in the structure at resonant frequencies, which provide the resulting modal shapes. It is needed to solve eigenvalue problem. The analysis consists of two steps: static analysis and eigenvalue analysis. The first step was static analysis for different electrical potential $\left\{Q\right\}=\{Q,Q=\stackrel{\mathrm{-}}{5,150}\text{V}\}$ and the pressure was equal to zero.

The second step was eigenvalue analysis of deformed vibroactive pad:

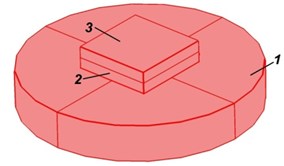
The next step is to create finite element model of vibroactive pad, when it is under the action of mechanical load. Thus the model was modified, by adding additional load (Fig. 4).

Fig. 4Modified vibroactive pad (1) with sample (2) and pressure tool (3)

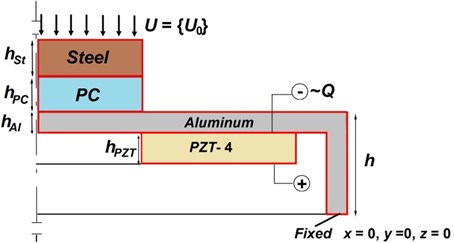
A 20×020 mm sample of polycarbonate and the pressure tool are projected in the middle of the vibroactive pad (Fig. 5.). The pressure device is modeled as non-deformable very stiff isotropic body from structural steel. Material properties of sample of polycarbonate and pressure tool were taken from COMSOL Multiphysics library (Table 1.). The thicknesses of steel ($h_{st}$) and polycarbonate ($h_{PC}$) are 3 mm. The pressure is defined as displacement ($U$) of upper steel’s plane by $z$ axis.

The full analysis consists also of two steps: static analysis and eigenvalue analysis. The first step was static analysis for different pressure $\left\{F\right\}=\{L,L=\stackrel{-}{1.01\cdot {10}^5,5.06\cdot {10}^5}\text{\hspace{0.17em}\hspace{0.17em}Pa}\}$.

The second step was eigenvalue analysis of deformed vibroactive pad:

Fig. 5Computational scheme of vibroactive pad with load (displacement (u, v, w), thickness of vibroactive pad (hAl), thickness of piezo ceramic ring (hPZT), thickness of specimen (hPC), thickness of pressure horn (hSt) and height of vibroactive pad (h))

3. Results

Frequencies of modes of vibrations were compared in order to check the validity of vibroactive pad modeling results with experimental data.

Numerical simulation results of vibroactive pad working at different regimes are presented in Fig. 6.

In order to determine the validity of mathematical model, it was compared with experimental results. The same vibration modes were obtained experimentally using the PHASE III PRISM system (measurement resolution – 20 nm, measurement range – 100 µm, largest part size – 1000 mm, working distance >1.3 m, data acquisition rate – 30 Hz, laser power – 20 mW, laser wavelength – 532 nm), produced by Hytec Company [10-12]. Vibration modes of made vibroactive pad (without load) are presented in (Fig. 7).

The comparison between the experimental research (Fig. 7) and simulation results (Fig. 6) shows that simulation results corresponds experimental results of vibroactive pad. The calculated difference of vibration frequency between experimental and simulated results was 5.4 % (the first form), 7.9 % (the second form), and 28.7 % (the third form). As it can be seen from the results, mathematical model is valid, and can be used for further analysis.

The next step of the investigation is to find operating frequencies of the vibroactive pad, when it is under load of 5.06·10⁵ Pa. For the development of vibroactive pad, which could be applied in the mechanical hot imprint process, it is useful to know vibration frequencies for corresponding modes under the pressure of vibroactive pad’s surface. It is impossible to observe vibration modes by using holographic interferometer, since loading device would cover the surface, which interests us, so the only way is to rely on numerical results. All these modes allow to achieve various optical properties of microstructure. The initial mathematical model (without load) of vibroactive pad was modified. The pressure as constrain displacement was added to the center of the pad. Pressure parameters are applied to area of the sample (20×20 mm). The vibration modes of vibroactive pad under the pressure of 5.06·10⁵ Pa are presented in the Fig. 8.

Fig. 6Vibration modes of model of vibroactive pad (without load): a)5.8 kHz and 10 V, b) 9.5 kHz and 60 V, c) 19.3 kHz and 70 V

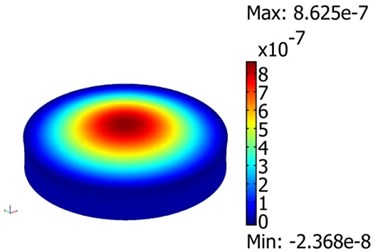
a)

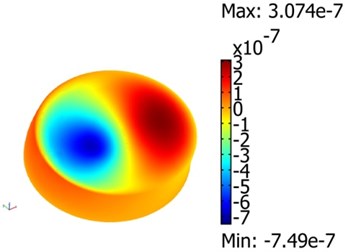
b)

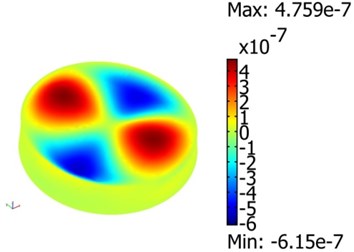
c)

Fig. 7Vibration modes of made vibroactive pad (without load): a) 5.2 kHz and 5 V, b) 8.8 kHz and 40 V, c) 15 kHz and 40 V

a)

b)

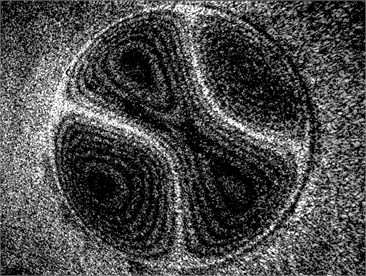
c)

The obtained results show, that the same vibration modes require higher frequencies. The frequency should be increased approximately by 20 % (the first and the second forms), in order to get the same vibration mode, as it would be without pressure.

Fig. 8Modes of vibroactive pad at 5.06⋅105 pressure: a)7 kHz and 10 V, b) 11.7 kHz and 60V, c) 19.9 kHz and 70 V

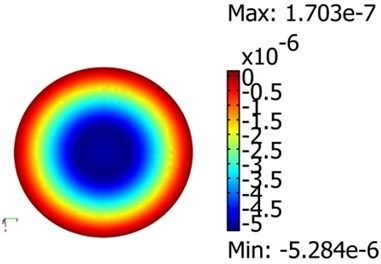
a)

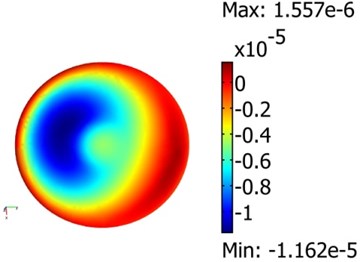
b)

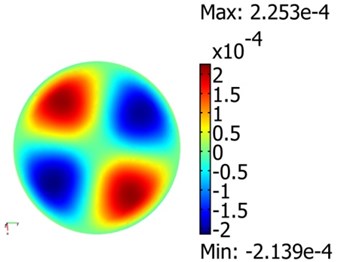
c)

4. Conclusions

In this paper vibroactive pad made from aluminum was numerically analyzed in order to determine its working regimes. Three vibration modes, natural frequencies and operating voltages of vibroactive pad were determined both numerically and experimentally. First three natural frequencies of modeled vibroactive pad are as following: 5.8; 9.5 and 19.3 kHz and experimental results for the same vibration modes are: 5.2; 8.8; and 15 kHz respectively. Difference between the results, which were obtained by analyzing the pad experimentally and numerically does not exceed 28.7 %, thus confirming the validity of mathematical model, and enabling to perform further numerical analysis of mechanically loaded pad. According to further numerical analysis, the frequency of vibroactive pad with applied mechanical load (5.06·10⁵ Pa pressure) at the center should be increased by about 20 %, i.e. first mode – 7 kHz, second mode – 11.7 kHz and third mode – 19.9 kHz in order to get the same vibration modes as it would be without load.