Dual quaternion-based inverse kinematics of dexterous finger

Chen, Jinbao; Han, Dong; Nie, Hong; Cheng, Mei

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2014

Check for updates

Dual quaternion-based inverse kinematics of dexterous finger

Jinbao Chen¹

Dong Han²

Hong Nie³

Mei Cheng⁴

^{1, 2, 3}College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

⁴Shanghai Institute of Satellite Engineering, Shanghai, 200240, China

Corresponding Author:

Jinbao Chen

Cite the article Download PDF

Downloads 1407

Abstract

The inverse kinematics solution of a dexterous robotic finger has a significant impact on the real-time control of the robotic hand. Therefore a rapid method for solving is needed. The classical homogeneous matrix transformation is the most popular method used in robot kinematics. However, for the multi degree-of-freedom (DOF) robotic finger, the matrix parameters cost much storage and the inverse matrix calculation requires a large amount of computational cost. So it is not conducive to the real-time control of the robotic hand. Therefore, a method based on dual quaternions is presented for analysing the kinematics of a multi-DOF (4-DOF) robotic thumb. Firstly, the kinematics equation is expressed by dual quaternions. Then the multivariate kinematic equations are converted to binary quadratic equations with methods of separating variables and variable substitution, which is relatively easy to obtain the closed-form solution of the inverse kinematics. Finally, it proves that the dual quaternions method has advantages over the homogeneous matrix transformation in storage and computational cost by the specific numbers for the robotic thumb, which is conducive to the real-time control of robotic hand.

1. Introduction

Dexterous finger is a multi-DOF and multi-link manipulator and its inverse kinematics have an important influence on the real-time control of dexterous hand. The thumb usually has the most DOFs in the whole hand, so the inverse kinematics of the thumb is the most complicated.

There are several methods for the formulation of the kinematic equations of manipulators with rigid links, including the homogeneous transformation and dual quaternion. The 4×4 matrix or the homogeneous transformation is an almost classical formulation of kinematic equation, which is a point transformation. The dual quaternion based on screw theory is the most efficient and compact way to express a screw displacement and is a line transformation [1, 2]. And Nichoals Aprove that the dual quaternion requires less computational time than the homogeneous transformation for the manipulators with more than 3 DOFs. And the homogeneous matrix needs 12 parameters to express the translation and rotation of rigid body while the dual quaternion 8. Therefore, the dual quaternion is an elegant and useful tool for kinematic analysis in many areas such as navigation [3], computer vision [4], inverse kinematics [5-7] and so on.

The relationship between the terminal and reference coordinates of multi-DOF manipulators is highly nonlinear [8], which makes the inverse kinematics difficult to solve. The solution of inverse kinematics can be classified into two types: closed-form analytical solution and numerical solution. Though the closed-form solution mainly relies on the kinematical structure of the manipulator, it is faster than the numerical solution and can avoid the singular problem and all the possible solutions of inverse kinematics can be given out [9]. The closed-form solution is the most ideal solution. The numerical solution is more general, but it can only find one solution for one set of initial values. In addition, numerical solution requires iterative calculation and a lot of iterative calculation can affect the computational time, which is not conducive to the real-time control. Furthermore, when the numerical method fails to converge, the solution of the inverse kinematics can’t be given out [9-11].

Many researchers choice the dual quaternion to solve the inverse kinematics of the multi-DOF robot manipulators because the kinematic equation with dual quaternion is more concise than that with homogeneous matrix, which is easy to get the closed-form solution. For example, Dgan, et al. adopt the dual quaternion to express the kinematic equation of 7-link 7R mechanism and get the closed-form solution by constructing Dixon resultant [6]; Ni Zhensong, et al. adopt the same method to get the closed-form solution of spatial 6R manipulator [7].

In this paper, the dual quaternion is applied in the inverse kinematics of 4-DOF thumb and the closed-form solution is presented. The algorithm is validated by an example. The whole process is very simple and easy to program, which is conducive to the real-time control of dexterous hand.

2. Quaternions and dual quaternions

2.1. Quaternions

The quaternion is a hypercomplex number with four parts and can well solve the problem of three dimensional space. A general quaternion has the following form [12]:

1

q = q_{0} + (q_{1} i + q_{2} j + q_{3} k) = s + v,

where $q_{0},$ $q_{1},$ $q_{2},$ $q_{3}$ are real numbers and $i,$ $j,$ $k$ are imaginary unit with the property $i^{2} = j^{2} = k^{2} =$ –1, $i j = k$ , $j k = i$ , $k i = j$ . The quaternion can also be divided into a scalar ( $s$ ) and a 3×1 vector ( $v$ ).

Conjugate of the quaternion can be expressed as:

2

q^{*} = q_{0} - q_{1} i - q_{2} j - q_{3} k .

The multiplication of two quaternions can be expressed as:

3

\begin{matrix} q q' = (q_{0} + q_{1} i + q_{2} j + q_{3} k) ({q_{0}^{'} + q}_{1}^{'} i + q_{2}^{'} j + q_{3}^{'} k) \end{matrix}

= q_{0} q_{0}^{'} - q_{1} q_{1}^{'} - q_{2} q_{2}^{'} - q_{3} q_{3}^{'} + (q_{1} q_{0}^{'} + q_{0} q_{1}^{'} - q_{3} q_{2}^{'} + q_{2} q_{3}^{'}) i

+ (q_{2} q_{0}^{'} + q_{3} q_{1}^{'} + q_{0} q_{2}^{'} - q_{1} q_{3}^{'}) j + (q_{3} q_{0}^{'} - q_{2} q_{1}^{'} + q_{1} q_{2}^{'} + q_{0} q_{3}^{'}) k .

2.2. Dual quaternions

Quaternions can only be used for analysing of the rotation of rigid body around a fixed point. However, a mathematical tool that can express both rotational and translational transformations in a spatial mechanism is needed [13]. Dual numbers were introduced by Clifford W. K. in 1873 and the dual quaternion is a dual number that has two quaternions. The dual quaternion has the following form:

4

\hat{q} = q + ε q_{ε},

where $q$ and $q_{ε}$ are quaternions and $ε$ is dual unit with the property $ε^{2} =$ 0.

Conjugate of the dual quaternion can be expressed as:

5

{\hat{q}}^{*} = q^{*} + ε q_{3}^{*} .

The multiplication of two dual quaternions can be expressed as:

6

\hat{q} \hat{Q} = (q + ε q_{ε}) (Q + ε Q_{ε}) = q Q + ε (q Q_{ε} + q_{ε} Q) .

The inverse of a dual quaternion can be expressed as:

7

{\hat{q}}^{- 1} = \frac{{\hat{q}}^{*}}{{‖\hat{q}‖}^{2}}, q_{0} \neq 0,

where ${‖\hat{q}‖}^{2}$ is the norm of the dual quaternion, which can be expressed as:

8

‖\hat{q}‖ = \sqrt{{\hat{q}}^{*} \hat{q}} = \sqrt{\hat{q} {\hat{q}}^{*}} = \sqrt{q q^{*} + ε (q q_{ε}^{*} + q_{ε} q^{*})} .

When the dual quaternion $\hat{q}$ is a unit dual quaternion, that is $‖\hat{q}‖ = 1$ , $\hat{q}$ should meet:

9

\begin{array}{l} q q_{ε}^{*} + q_{ε} q^{*} = 0, \\ q q^{*} = 1, \end{array}

then ${\hat{q}}^{- 1} = {\hat{q}}^{*}$ [14].

The rigid body motion in three-dimensional space can be decomposed into rotation and translation. Let the unit quaternion ( $R$ ) express the rotation and $d$ express the translation vector. Therefore, the rigid motion can be described in dual queternions like this:

10

\hat{Q} = R + ε (\frac{d R}{2}),

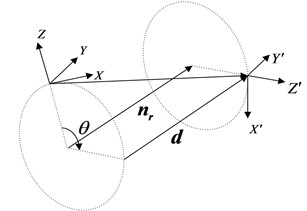
where $R = c o s (θ / 2) + s i n (θ / 2) n_{r}$ and $θ$ is rotation angle and $n_{r}$ is direction vector of rotation axis (Fig. 1).

Fig. 1The rotation and translation expressed by dual quaternions

3. Kinematics of dexterous finger

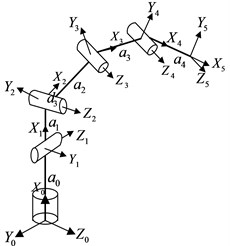
This paper uses the 4-DOF thumb as an example to illustrate the method that adopts dual queternions to solve the inverse kinematics of dexterous finger. The mechanical structures of the thumb are shown in Fig. 2. And the relationship between the coordinate systems is shown in Fig. 3.

Fig. 24-DOF thumb

Fig. 3Relationship between the coordinate systems

The Denavit-Hartenberg (D-H) parameters of the thumb are listed in Table 1.

Table 1D-H parameters of the thumb

$i$	$α_{i - 1}$ / (°)	$a_{i - 1}$ / mm	$d_{i}$ / mm	$θ_{i}$ / (°)
1	90.0	10	0	$θ_{1}$
2	–90.0	17	0	$θ_{2}$
3	40.0	37	7	$θ_{3}$
4	0	38	0	$θ_{4}$

In this paper, $d_{n}$ is defined as the distance from $X_{n - 1}$ to $X_{n}$ along the $Z_{n - 1}$ axis; the other parameters are defined according to the classical definitions.

According to Fig. 3 and Table 1, the transformations of each link lever are expressed by dual queternions as follow:

11

\begin{matrix} {\hat{Q}}_{0}^{1} = {\hat{P}}_{0}^{X} (a_{0}) {\hat{R}}_{0}^{Y} (θ_{1}) = (1 + \frac{ε (a_{0} i)}{2}) (c o s (\frac{θ_{1}}{2}) + s i n (\frac{θ_{1}}{2}) j + ε * 0), \end{matrix}

12

{\hat{Q}}_{1}^{2} = {\hat{P}}_{1}^{X} (a_{1}) {\hat{R}}_{1}^{Z} (θ_{2}) = (1 + \frac{ε (a_{1} i)}{2}) (c o s (\frac{θ_{2}}{2}) + s i n (\frac{θ_{2}}{2}) k + ε * 0),

13

{\hat{Q}}_{2}^{3} = {\hat{P}}_{2}^{Z} (d_{3}) {\hat{R}}_{2}^{X} (α_{2}) {\hat{P}}_{2}^{X} (a_{2}) {\hat{R}}_{2}^{Z} (θ_{3})

= (1 + \frac{ε (d_{3} k)}{2}) (c o s (\frac{α_{2}}{2}) + s i n (\frac{α_{2}}{2}) i + ε * 0) (1 + \frac{ε (a_{2} i)}{2})

∙ (c o s (\frac{θ_{3}}{2}) + s i n (\frac{θ_{3}}{2}) k + ε * 0),

14

{\hat{Q}}_{3}^{4} = {\hat{P}}_{3}^{X} (a_{3}) {\hat{R}}_{3}^{Z} (θ_{4}) = (1 + \frac{ε (a_{3} i)}{2}) (c o s (\frac{θ_{4}}{2}) + s i n (\frac{θ_{4}}{2}) k + ε * 0),

15

{\hat{Q}}_{4}^{5} = {\hat{P}}_{4}^{X} (a_{4}) = (1 + \frac{ε (a_{4} i)}{2}),

where $a_{0}$ , $a_{1}$ , $a_{2}$ , $a_{3}$ , $a_{4}$ , $α_{2}$ , $d_{3}$ are known D-H parameters; $θ_{n}$ represents the angle displacement of the $n$ -joint, $n = 1,2, 3,4$ . The position and orientation of the end of the robotic thumb in the Cartesian coordinates are expressed by a dual queternion as follow:

16

\hat{N} = (r_{0} + r_{i} i + r_{j} j + r_{k} k) + ε (s_{0} + s_{i} i + s_{j} j + s_{k} k) .

where $r_{0}$ , $r_{i}$ , $r_{j}$ , $r_{k}$ , $s_{0}$ , $s_{i}$ , $s_{j}$ and $s_{k}$ represent the position-orientation parameters of the end.

So, the kinematics equation of the thumb is given by:

17

{\hat{Q}}_{0}^{1} {\hat{Q}}_{1}^{2} {\hat{Q}}_{2}^{3} {\hat{Q}}_{3}^{4} {\hat{Q}}_{4}^{5} = \hat{N} .

Eq. (17) is separated variables. A new equation is given by:

18

{\hat{Q}}_{0}^{1} {\hat{Q}}_{1}^{2} = \hat{N} {\hat{Q}}_{2}^{3}^{- 1} {\hat{Q}}_{3}^{4}^{- 1} {\hat{Q}}_{4}^{5}^{- 1} .

It is easy to prove that ${\hat{Q}}_{2}^{3}$ , ${\hat{Q}}_{3}^{4}$ and ${\hat{Q}}_{4}^{5}$ meet Eq. (9), so their inverse is equal to their conjugate. Therefore, Eq. (18) can also be expressed as:

19

{\hat{Q}}_{0}^{1} {\hat{Q}}_{1}^{2} = \hat{N} {\hat{Q}}_{2}^{3}^{*} {\hat{Q}}_{3}^{4}^{*} {\hat{Q}}_{4}^{5}^{*} .

Setting left and right sides of Eq. (19) as $\hat{U}$ and $\hat{V}$ :

20

\hat{U} = \hat{V},

where:

21

\hat{U} = U_{1} + ε U_{2} = u_{11} + u_{12} i + u_{13} j + u_{14} k + ε (u_{21} + u_{22} i + u_{23} j + u_{24} k),

22

\hat{V} = V_{1} + ε V_{2} = v_{11} + v_{12} i + v_{13} j + v_{14} k + ε (v_{21} + v_{22} i + v_{23} j + v_{24} k) .

If two dual queternions are equal, each element should be equal. So, $u_{1 i} = v_{1 i}$ , $u_{2 i} = v_{2 i}$ ( $i =$ 1, 2, 3, 4) and we get:

23

D_{j} [\begin{array}{l} c θ_{1} c θ_{2} \\ s θ_{1} c θ_{2} \\ c θ_{1} s θ_{2} \\ s θ_{1} s θ_{2} \end{array}] = C_{j}, j = 1, 2,

where $c θ_{k} = c o s (θ_{k} / 2)$ , $s θ_{k} = s i n (θ_{k} / 2)$ , ( $k =$ 1, 2, 3, 4) and $D_{j}$ is a 4×4 matrix that is decided by the D-H parameters of the thumb and the position and orientation of end-effector; $C_{j}$ is a 4×1 vector, whose elements are the linear expression of $c θ_{3}$ $c θ_{4}$ , $s θ_{3}$ $c θ_{4}$ , $c θ_{3}$ $s θ_{4}$ and $s θ_{3}$ $s θ_{4}$ .

Form Eq. (23), we can get:

24

{D_{1}}^{- 1} C_{1} = {D_{2}}^{- 1} C_{2} .

The left and right sides of Eq. (24) are divided by $c θ_{3}$ $c θ_{4}$ and we get equations as follow:

25

E q_{e} (t_{3}, t_{4}) = a_{e} + m_{e} t_{3} + n_{e} t_{4} + p_{e} t_{3} t_{4} = 0, e = 1, 2, 3, 4,

where $t_{3} = s θ_{3} / c θ_{3}$ , $t_{4} = s θ_{4} / c θ_{4}$ , and $a_{e}$ , $m_{e}$ , $n_{e}$ , $p_{e}$ are known quantity and decided by the D-H parameters of the thumb and the position and orientation of end-effector. Eq. (25) are binary quadratic equations. Hence, it is easy to get the closed-form solution of Eq. (25), that is to say, we can get the closed-form solution of $θ_{3}$ and $θ_{4}$ . The closed-form solution of $θ_{1}$ and $θ_{2}$ can be similarly solved through Eq. (23) with known $θ_{3}$ and $θ_{4}$ .

4. Verification and comparison

4.1. Verification with an example

Firstly, a simple example is given to illustrate the validity of the proposed method. Let $θ_{1} =$ 0.353 rad, $θ_{2} =$ 0.434 rad, $θ_{3} =$ 0.625 rad, $θ_{4} =$ 0.764 rad, which are the desired values. Then the position and orientation of the end-effector is calculated by the desired angle displacements of each joint, which is expressed by the dual quaternion as follow:

26

\hat{N} = (0.5943 + 0.4294 i - 0.0536 j + 0.6779 k)

+ ε (- 0.0128 + 0.0487 i - 0.0064 j - 0.0123 k) .

Substitute the D-H parameters and Eq. (26) in Eq. (25) and get:

27

0.5671 - 0.6969 t_{3} + 1.1478 t_{4} + 2.5524 t_{3} t_{4} = 0,

- 9.1484 + 7.8760 t_{3} + 14.4637 t_{4} + 6.0844 t_{3} t_{4} = 0,

- 1.8693 + 1.9064 t_{3} + 3.0650 t_{4} + 0.1278 t_{3} t_{4} = 0,

- 2.3280 + 2.1035 t_{3} + 4.0748 t_{4} + 0.1538 t_{3} t_{4} = 0 .

The solution of Eq. (27) is $t_{3} =$ 0.3262, $t_{4} =$ 0.4002, that is to say, $θ_{3}^{'} = 0.6304$ , $θ_{4}^{'} = 0.7610$ . Substitute $θ_{3}^{'}$ and $θ_{4}^{'}$ in Eq. (23) and get $θ_{1}^{'} = 0.3513,$ $θ_{2}^{'} = 0.4315.$ The results of inverse kinematics testify that the algorithm is effective.

Secondly, another example based on trajectories is presented to illustrate the practicality of the method. The trajectories are planned in joint space. For the stability of the manipulator’s motion, linear interpolation taking parabolic transition is adopted to plan the trajectories of each joint. And the planned trajectories of the four joints are respectively shown in Fig. 4(a), Fig. 5(a), Fig. 6(a) and Fig. 7(a). According to the trajectories in joint space, the trajectories of the end of the robtic thumb in Cartesian space can be computed. So, the inverse kinematics solution can be gotten by using the proposed method with knowing the trajectories of the end, as shown in Fig. 4(b), Fig. 5(b), Fig. 6(b) and Fig. 7(b). The computed results of the inverse kinematics are almost equal to the planned trajectories in joint space by comparing the Fig. 4-7. Therefore, the dual quaternion can be used for solving the inverse kinematics of the multi-DOF manipulator in practice.

4.2. Comparison with homogeneous transformation

The above two examples show the feasibility of the dual quaternion for solving the inverse kinematics. Furthermore, the dual quaternion outperforms homogeneous transformation in three aspects for the multi-DOF (more than 3 DOFs) manipulator [1], as follow:

1) Storage cost: For one transformation, the dual quaternion requires eight memory locations, while homogeneous transformation needs12, since the elements of the fourth row are known constants. According to Eq. (17), we know that the dual quaternion method requires 48 memory locations at least for an inverse kinematic computation, while homogeneous transformation requires 72. It is obvious that the storage cost of the dual quaternion method is minimum.

2) Computational cost: We define that the sign+ represents addition and subtraction operations and the sign* represents multiplication operations. The multiplication of two 4×4 homogeneous matrices needs 48* and 36+ [1]. The inverse of homogeneous matrix requires 9* and 6+. The multiplication of two dual quaternions needs 48* and 36+. The inverse of dual quaternions needs no computational cost. Therefore, the computation of (18) needs 219* and 162+ for homogeneous transformation, while 192* and 144+ for the dual quaternion.

3) Computational time: The storage and computational cost can both affect the computational time. Fetching an operand from memory will cost computational time. And the computational time of an addition is less than one multiplication. It turns out that the computational time of homogeneous transformation is more than the dual quaternion for the inverse kinematics of 4-DOF thumb according to the conclusions of 1) and 2).

In one word, the homogeneous transformation method needs more storage and computational cost than the dual quaternion method, which leads to more computational time that the former requires than the latter.

5. Conclusions

The dual quaternion is applied in the inverse kinematics solution of 4-DOF dexterous thumb, which greatly simplifies the process of getting the closed-form solution and provides a new thinking for the inverse kinematics solution of multi-DOF dexterous finger.

Through comparing with the homogeneous transformation, we can conclude that the dual quaternion can simplify the kinematics equation, effectively reduce the storage and computational cost, greatly improve computational speed and satisfy the requirements of the real-time control of dexterous hand. However, the dual quaternion has no advantage over the homogeneous transformation for the finger with less than 4 DOF.

References

Nichoals A. Aspragathos, John K. Dimitros A comparative study of three methods for robot kinematics. IEEE Transactions on Systems, Vol. 28, Issue 2, 1998, p. 135-145.

Search CrossRef
Sariyildiz E., Temeltas H. Solution of inverse kinematic problem for serial robot using dual quaterninons and plücker coordinates. International Conference on Advanced Intelligent Mechatronics, 2009, p. 338-343.

Search CrossRef
Li Jing, Wang Huinan, Liu Haiying Application of dual quaternion in spacecraft relative navigation. Journal of Applied Sciences, Vol. 30, Issue 3, 2012, p. 311-316, (in Chinese).

Search CrossRef
Konstantinos Daniilidis Hand-eye calibration using dual quaternions. The International Journal of Robotics Research, Vol. 18, 1999, p. 286-298.

Search CrossRef
Perez Alba, McCarthy J. M. Dual quaternion synthesis of constrained robotic systems. Journal of Mechanical Design, Vol. 126, 2004, p. 425-435.

Search CrossRef
Gan D., Liao Q., Wei S., et al. Dual quaternion-based inverse kinematics of the general spatial 7R mechanism. Journal of Mechanical Engineering Science, Vol. 222(c), 2008, p. 1593-1598.

Search CrossRef
Ni Zhensong, Liao Qizheng, Wei Shimin, et al. Dual four element method for inverse kinematics analysis of spatial 6R manipulator. Journal of Mechanical Engineering, Vol. 45, Issue 11, 2009, p. 25-29, (in Chinese).

Search CrossRef
Rodolphe J. Gentili, Hyuk Oh, Javier Molina, et al. Cortex inspired model for inverse kinematics computation for a humanoid robotic finger. 34th Annual International Conference of the IEEE EMBS, 2012, p. 3052-3055.

Search CrossRef
Yang Si, Qingxuan Jia, Gang Chen, et al. A complete solution to the inverse kinematics problem for 4-DOF manipulator robot. 8th Conference on Industrial Electronics and Applications, 2013, p. 1880-1884.

Search CrossRef
Andrew A. Goldenberg, Member B. Benhabib, et al. A complete generalized solution to the inverse kinematics of robots. IEEE Journal of Robotics and Automation, Vol. 1, Issue 1, 1985, p. 14-20.

Search CrossRef
Jing Huang, Xianlun Wang, Dongsheng Liu, et al. A new method for solving inverse kinematics of an industrial robot. International Conference on Computer Science and Electronics, 2012, p. 53-56.

Search CrossRef
Hoang-Lan Pham, Véronique Perdereau, Bruno Vilhena Adorno, et al. Position and orientation control of robot manipulators using dual quaternion feedback. The International Conference on Intelligent Robots and Systemsg, 2010, p. 658-663.

Search CrossRef
Liu Yanzhu The mathematical expression of rigid body attitude. Mechanics in Engineering, Vol. 33, Issue 1, 2008, p. 98-101, (in Chinese).

Search CrossRef
Nan Ji, Wang Jianguo, Chen Jianyu Rigid dual quaternions related problems. Fire Control and Command Control, Vol. 37, 2012, p. 15-17, (in Chinese).

Search CrossRef

About this article

Received

29 October 2013

Accepted

22 August 2014

Published

30 September 2014

Keywords

inverse kinematics

dexterous finger

real-time control

homogeneous matrix transformation

dual quaternion

Acknowledgements

The authors would like to thank the anonymous reviewers for their critical and constructive review of the manuscript. This work was supported by National Natural Science Foundation of China (Grant No. 51105196), Natural Science Foundation of Jiangsu Province (Grant No. BK2011733), Science and Technology Innovation Fund of Shanghai Aerospace (Grant No. SAST201320), and Shanghai Key Laboratory of Deep Space Exploration Technology.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.