Stochastic bifurcation characteristics of cantilevered piezoelectric energy harvester

1. Introduction

Piezoelectric ceramics is a kind of smart material. It can be used to convert mechanical energy into electrical energy, which is known as piezoelectric effect. Based on this effect, piezoelectric energy harvester can be designed to gather vibration energy of structures. Compared with other kinds of power generation systems, piezoelectric energy harvester has many advantages, such as small size, high electro-mechanical conversion efficiency, long service life, and low cost, which cause it be applied as green energy widely.

Many scholars studied piezoelectric energy harvester. DuToit designed MEMS-scale piezoelectric mechanical vibration energy harvesters firstly [1]. Erturk developed the mechanical model of cantilevered piezoelectric vibration energy harvesters [2]. Priya proposed the criterion for material selection in design of bulk piezoelectric energy harvesters [3]. Liao studied parameters optimization and power characteristics of piezoelectric energy harvesters with RC circuit [4]. Although many advances were obtained, the modeling problem limits the application of cantilever piezoelectric energy harvester in industry fields. In order to optimize piezoelectric energy harvester effectively, it is necessary to build a model in high accuracy to describe the nonlinear characteristics of piezoelectric energy harvester.

Due to the hysteretic characteristics of piezoelectric ceramics, most of the piezoelectric models were shown as equations with subsection function or double integral function, which were hard to be analyzed in theory [5-9]. Usually, research results could only be obtained by numerical or experiment method [10, 11]. In this paper, hysteretic nonlinear theory was introduced to develop a new kind of continuous piezoelectric model, and then stochastic bifurcation characteristics of cantilevered piezoelectric energy harvester were analyzed.

2. Hysteretic nonlinear model of piezoelectric energy harvester

The voltage-displacement curve of piezoelectric ceramics was shown in Fig. 1. Obviously, there is hysteretic nonlinearity in piezoelectric ceramics.

Fig. 1The displacement-voltage curves of piezoelectric ceramics

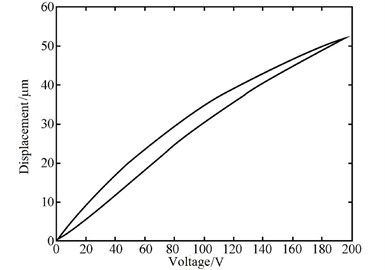
In this paper, Von del Pol hysteretic model was introduced to describe the hysteretic nonlinear characteristics of piezoelectric ceramics. The initial Von del Pol hysteretic model describes hysteretic loop which is symmetrical about the initial point ($0,0$). It can be shown as follows:

where $f_0\left(x\right)$ is skeleton curve of hysteretic loop and usually expressed in polynomial function, $a$ and $b$ are coefficients which determine the difference between the skeleton curve and the real curve. The essence of Von del Pol item $a\left[1-{\left(\frac{x}{b}\right)}^2\right]\dot{x}$ are two parabolic lines which are symmetrical about the original point ($0,0$).

Supposing the displacement-voltage curves of piezoelectric ceramics is symmetrical about the point $G(V_0,x_0)$, it can be shown as follows:

where $V$ is voltage, $x$ is displacement, $b_i$$\text{(}i=1,2,3,4\text{)}$ are coefficients, skeleton curve is chosen as $f_0\left(x\right)=b_{1}x+b_2{x}^3$.

$b_4=x_0$ since the loading curve have the same value as the unloading curve when $x=\text{0}$, and ${\sigma }_0-b_1{x}_0-b_2{x}_0^3=0$ because the initial voltage of piezoelectric ceramics is zero. Thus, Eq. (2) can be rewritten as follows:

where $a_1=b_1+3b_2{x}_0^2$, $a_2=-3b_2{x}_0$, $a_3=b_2$, $a_4=\frac{2b_3}{b_4}$, $a_5=\frac{b_3}{b_4^2}$.

The structure of cantilevered piezoelectric energy harvester was shown in Fig. 2. It can be regarded as cantilever composite beam. The mechanical model of cantilevered piezoelectric energy harvester was shown in Fig. 3, where the thickness of adhesive layer was ignored.

According to Hamilton's principle, we obtained:

where $T$ is kinetic energy of structure, $U$ is potential energy of structure, $W_e$ is electric energy of piezoelectric ceramics, $W$ is work done by external force:

where ${\rho }_i$$(i=\stackrel{-}{s},\stackrel{-}{p})$ is density of substrate and PZT piezoelectric ceramics, where the subscript $\stackrel{-}{s}$ is substrate, $\stackrel{-}{p}$ is PZT piezoelectric ceramics; $V_i$ is volume, ${\sigma }_i$ is stress, ${\epsilon }_i$ is strain; $u=u(x,t)$ is deflection of composite cantilever beam, $E_3$ is electric field intensity, $D_3$ is electrostrictive displacement, $F=e\varsigma \left(t\right)$ is axial stochastic excitation, $e$ is intensity of stochastic excitation, $\varsigma \left(t\right)$ is Gauss white nosie whose mean is zero and intensity is $2D$, $\varphi$ is electric potential, $\stackrel{-}{q}$ is electric charge.

Fig. 2The structure of cantilevered piezoelectric energy harvester

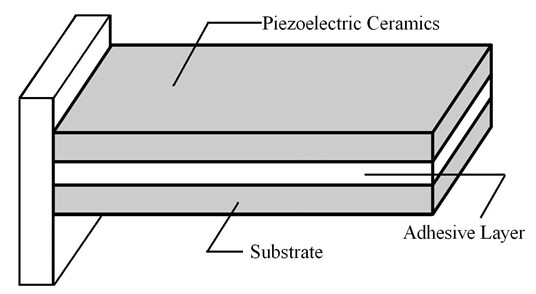
Fig. 3The mechanical model of cantilevered piezoelectric energy harvester

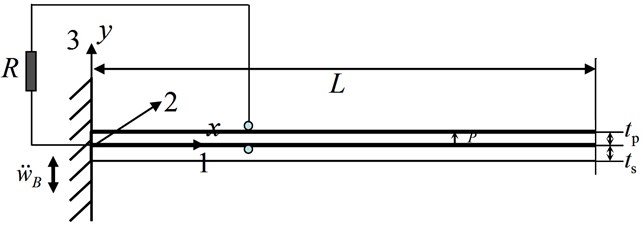
The dynamic equation of piezoelectric cantilever beam subjected to axial stochastic excitation can be obtained as follows:

where ${\zeta }_m$ is damping, $k$ is stiffness, $\vartheta$ and ${\alpha }_i$$(i=1,2,3,4)$ are coefficients.

Substituting Eq. (3) into Eq. (9), we obtained:

where:

3. Stochastic stability analysis of system

Let $x=q$, $\dot{x}=p$, Eq. (10) can also be shown as follows:

The Hamiltonian function of Eq. (19) can be shown as follows:

According to the quasi-nonintegrable Hamiltonian system theory, the Hamiltonian function $H\left(t\right)$ converges weakly in probability to an one-dimensional Ito diffusion process. The averaged Ito equation about the Hamiltonian function can be shown as follows:

where $B\left(t\right)$ is standard Wiener process, $m\left(H\right)$ and $\sigma \left(H\right)$ are drift and diffusion coefficients of Ito stochastic process, which can be obtained in stochastic averaging method as follows:

where $R$ is the solution of the following equation:

Then the associated largest Lyapunov exponent of the system is:

Now the local stochastic stability of the system can be discussed as follows:

1) The trivial solution $H=0$ is locally asymptotic stable if and only if $\lambda <$0, which means the vibration amplitude of the system will tend to zero;

2) The trivial solution $H=0$ is locally asymptotic unstable if and only if $\lambda >$0, which means the vibration amplitude of the system will tend to be large;

3) Bifurcation should appear near the trivial solution $H=0$ if and only if $\lambda =$0, which means the vibration amplitude of the system will jump between the small value and the large value.

The largest Lyapunov exponent can only estimate the local stability. In this paper, the boundary classification method was used to analyze the global stability of the trivial solution of the system. Generally, the boundaries of diffusion process are singular, and the boundary classification is often determined by diffusion exponent, drift exponent and character value [12].

When $H\to 0\text{,}$ we obtained that:$m\left(H\right)\to \text{O}\left(H\right)\text{,}$${\sigma }^2\left(H\right)\to \text{O}\left(H^2\right)\text{,}$${\alpha }_l=2\text{,}$${\beta }_l=1\text{,}$$c_l=\frac{\sqrt{\text{2}}{\vartheta }^{\text{2}}{\alpha }_{\text{1}}{a}_4}{D{e}^2}$, where ${\alpha }_l$ is diffusion exponent, ${\beta }_l$ is drift exponent, $c_l$ is character value, $l$ is left boundary. Thus, the left boundary $H=0$ belongs to the first kind of singular boundary.

According to the classification for singular boundary, we obtained:

1) The left boundary $H=0$ is repulsively natural if $c_l>$1;

2) The left boundary $H=0$ is strictly natural if $c_l=$1;

3) The left boundary $H=0$ is attractively natural if $c_l<$1.

When $H\to \infty \text{,}$ we obtained that: $m\left(H\right)=\text{O}\left(H^{\text{8}/\text{7}}\right)\text{,}$${\sigma }^2\left(H\right)=\text{O}\left(H^{\text{9}/\text{7}}\right)\text{,}$${\alpha }_r=\frac{9}{7}\text{,}$${\beta }_r=\frac{8}{7}\text{,}$ where $r$ is the right boundary. Thus, the right boundary $H=\infty$ belongs to the first kind of singular boundary. Thus, the right boundary$H=\infty$ is an entrance boundary.

The necessary and sufficient conditions for globally asymptotic stability of the trivial solution require that the left undary be attractively natural and the right boundary be entrance. Thus, the trivial solution $H=0$ is globally asymptotically stable if and only if $c_l<$1, which means $\sqrt{\text{2}}{\vartheta }^2{\alpha }_1{a}_4<e^{2}D$. The influence of the character value to the stability was shown in Fig. 4.

Fig. 4The influence of the character value to the stability

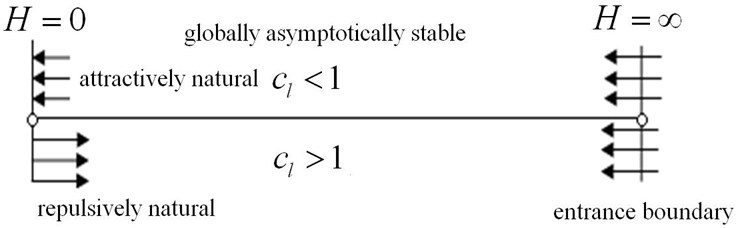
4. Stochastic bifurcation and simulation

The averaged FPK equation of Eq. (19) is:

where $f$ is probability density.

Thus, the stationary probability density function of the system is:

where $\stackrel{-}{A}$ is a normalization constant, $\eta =\frac{\sqrt{\text{2}}{\vartheta }^{\text{2}}{\alpha }_{\text{1}}{a}_4-2D{e}^2}{D{e}^2}$.

The result of numerical simulation were shown in Fig. 5-8, where $k=\text{0.5}$, $D=\text{0.5}$, $l=\text{1}$, ${\xi }_m=\text{0.05}$, $M=\text{40}$, $E=\text{2×}{\text{10}}^{\text{11}}$, $A=\text{8×}{\text{10}}^{\text{-4}}$, $I=\text{6×}{\text{10}}^{\text{-11}}$, $a_1=\text{3.8}$, $a_2=\text{–0.27}$, $a_3=\text{0.014}$.

Fig. 5The steady-state probability density of the system when a4=2 and a5=4.5

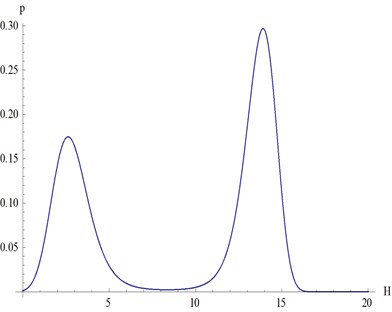
Fig. 6The joint probability density of the system when a4=2 and a5=4.5

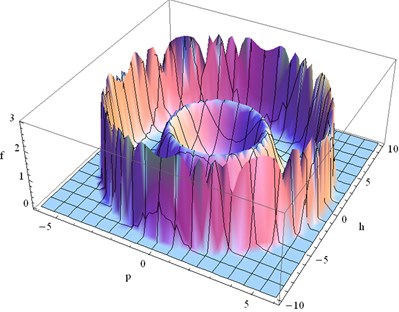
Fig. 7The steady-state probability density of the system when a4=3.5 and a5=4

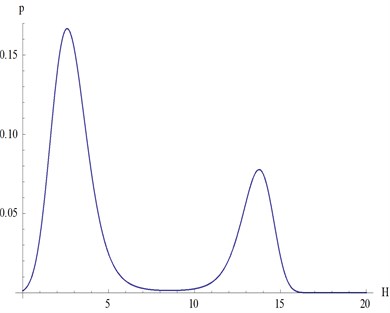
Fig. 8The joint probability density of the system when a4=3.5 and a5=4

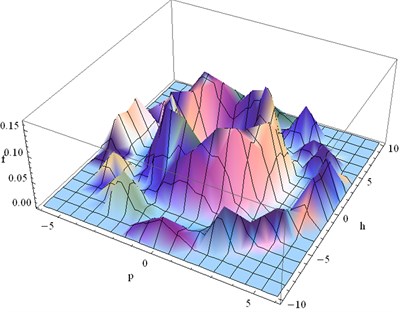
From Fig. 5-8, we can see that:

1) The hysteretic nonlinear damping coefficients $a_i$ ($i=4,5$) can induce stochastic Hopf bifurcation of the system. From Fig. 6 and Fig. 8, we can obviously see that there are two limit cycles in the stationary probability density, which means that there are two vibration amplitudes whose probability are both very high. Jumping phenomena between the two vibration amplitudes will appear when the conditions are changed;

2) The stationary probability density of the response of the system can be changed through adjusting the parameters $a_i$ ($i=4,5$). It means that different PZT piezoelectric ceramics materials will cause different vibration amplitudes of the system since the parameters $a_i$ ($i=4,5$) are determined by PZT piezoelectric ceramics. It provide a way to improve the efficiency of the energy harvester since the stationary probability density of the big vibration amplitude can be increased by choosing appropriate PZT piezoelectric ceramics.

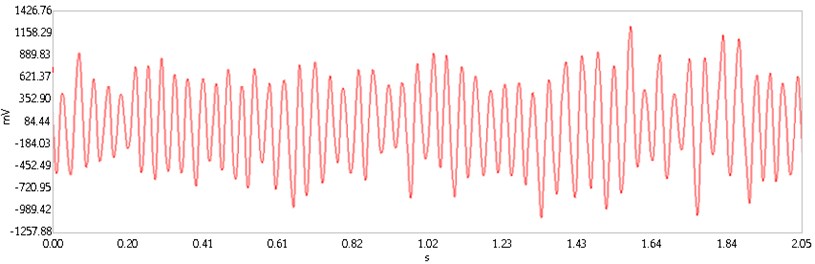
The experimental results of cantilevered piezoelectric energy harvester were shown in Fig. 9 and Fig. 10, where the vibration amplitude was shown as output voltage of sensor. We can see that system paremeters $a_i$ ($i=4,5$) can influence the vibration of the system, and jumping phenomena between the two vibration amplitudes appears when the conditions are changed.

Fig. 9The response of cantilevered piezoelectric energy harvester when a4=3.5 and a5=4

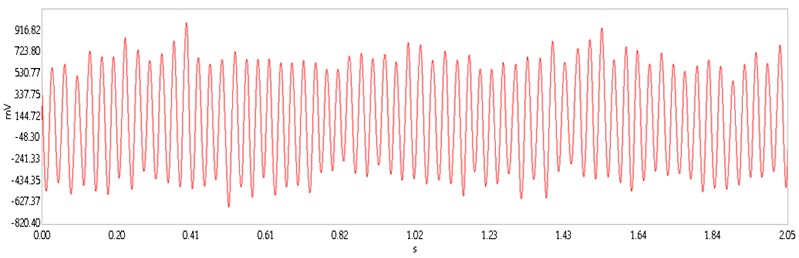
Fig. 10The response of cantilevered piezoelectric energy harvester when a4= 2 and a5= 4.5

5. Conclusions

Stochastic bifurcation characteristics of cantilevered piezoelectric energy harvester had been studied in this paper. Von de Pol differencial item was introduced to interpret the hysteretic phenomena of piezoelectric ceramics, and then the nonlinear dynamic model of piezoelectric cantilever beam subjected to axial stochastic excitation was developed. The stochastic stability of the system was analyzed, and the steady-state probability density function and the joint probability density function of the dynamic response of the system were obtained, and then the conditions of stochastic Hopf bifurcation were analyzed. Numerical simulation shows that stochastic Hopf bifurcation appears when bifurcation parameter varies, which can increase vibration amplitude of cantilever beam system and improve the efficiency of piezoelectric energy harvester. Finally, the theoretical and numerical results were proved by experiments. The results of this paper are helpful to application of cantilevered piezoelectric energy harvester in engineering fields.