Abstract
For geogrid reinforced soil retaining walls, there are no reasonable analysis theories and design methods. Its seismic reinforcement mechanism has not been clear. A nonlinear finite difference method is applied to analyze reinforced internal forces of geogrid reinforced soil retaining walls under different design parameters. An elastic-plastic model is used to simulated soils. The coupled elastic parameters are used to describe the interaction between soils and geogrids. The analysis parameters include reinforcement lengths, reinforcement spacing, distribution forms of geogrid layers, the stiffness of geogrids, earthquake intensities, stiffness of backfill soils, unit weights and panel thicknesses. Finally, the shaking table test model of a geogrid reinforced soil retaining wall is introduced. Seismic strains of geogrids are tested and are compared with numerical simulation results. Some conclusions are achieved such as distribution characters of seismic residual deformations of reinforced walls, coupled shear stresses between geogrids and soils, some sensitive impact parameters on reinforced internal forces of geogrids. The geogrids located in the middle layer of the reinforced zone play an important role. Calculation results will offer references for seismic designs of geogrid reinforced soil retaining walls.
1. Introduction
Geogrid reinforced soil retaining walls are relative flexible retaining soil structures. Protruding swelling deformations and overturning multiple damages of geo-grid reinforced retaining walls can occur respectively under earthquakes, for example, during Chi-Chi earthquake in Taiwan and the earthquake in El Salvador [1-2]. At present, the reinforcement mechanism of seismic behavior is unclear, and there is no strict analysis theory and design method of this reinforcement structure, and there is no reasonable standard for seismic design.
In recent years, there is some research work on engineering functions of geo-grid reinforced soil retaining walls. Based on geo-grid reinforced soil retaining walls with integral panel on Gan Long Railway, Yang Guangqing [3] made some site situ experiment tests such as the base stress of reinforced earth wall, the earth pressure of reinforced wall back, the stretching deformation of geo-grid, and the horizontal deformation of wall so on. Andrzej Sawicki [4] gave the creep analysis technique for reinforced soil retaining wall and the method of assessing the initial stress in reinforced zone, in which the soil is assumed in a plastic state and the reinforced body is viscoelastic, and then the theory is proved to be in good agreement with the experiment by reinforced wall model test. Deepankar Choudhury [5] presents a methodology for seismic design of rigid water front-retaining walls and proposes simple design factors for sliding stability under seismic conditions. The conventional pseudo-static approach has been used for the calculation of seismic forces, while Westergaard’s approach has been used for the calculation of the hydrodynamic pressure. Chia-Cheng Fan [6] used three-dimensional non-linear finite element analysis to investigate the three-dimensional behavior of a reinforced earth-retaining structure within a V-shaped valley focusing on reinforcement stress and deformation. Assaf Klar [7] presented a new computer-based method for the analysis of reinforced soil walls that took into accounts for the interaction between the facing and the soil reinforcement layers. This method required full compatibility between the reinforcement layers and the deforming wall, and was solved as an optimization problem for this constraint. Huei-Tsyr Chen et al. [8] conducted a series of centrifuge VGREW models to simulate a clayey vertical geotextile-reinforced earth wall (VGREW) in a wet state due to poor drainage conditions after several consecutive days of heavy rainfall. K. Z. Z. Lee [9] presented the results of numerical simulation of three full-scale geosynthetic-reinforced soil walls that were seismically loaded by a shaking table. The calculated results indicated seismic wall displacement decreases with decreasing reinforcement spacing. Factors responsible for comparison discrepancy are discussed. Variability within the measured data is thought to have contributed to some of the comparison discrepancy. J. Izawa [10] tested the effect of the stability of the geo-grid reinforced retaining wall under saturated condition of backfill sand by conducting centrifuge shaking table test. In order to study factors affecting the cyclic and post-cyclic pullout behavior of different geogrids embedded in a compacted granular soil, Nicola Moraci [11] carried out the results of a wide experimental research. The influence of the same factors on the pullout behavior in terms of accumulated displacements and deformations are analyzed.
In this paper, a finite difference method is applied to research characters of reinforced internal forces of geogrid under influences of various seismic design parameters for geogrid reinforced soil retaining walls with integral panel. FLAC3D is the application of Lagrange method in geotechnical mechanics. It is a fully nonlinear analysis method based on explicit difference method, and the mechanical behavior of geological material and geotechnical engineering can be calculated geological materials. As FLAC program is primarily developed for geotechnical engineering applications and the development of rock mechanics calculation procedures, it includes procedures that reflect the special calculation function in mechanical effects of geo-materials, it can calculate highly nonlinear (including strain hardening/softening), irreversible shear failure and compaction, viscoelastic (creep), porous medium solid – fluid coupling and dynamic behaviors.
2. Analysis model
2.1. Geometrical structure and load
The base model of a geogrid reinforced soil retaining wall is given in Fig. 1. The height of reinforced wall () is 6.0 m. The thickness of reinforced wall is 24 cm. The wall is made of concrete. The thickness of foundation is 3.0 m. The geogrid length () is 0.7 times of the reinforced height. The reinforcement spacing is 0.6 m.
Fig. 1Schematic diagram of standard reinforced structure model
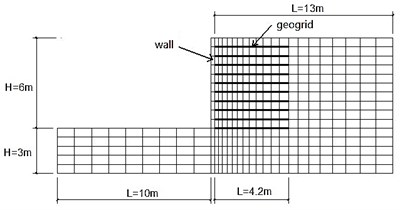
Fig. 23D mesh model of reinforced structure
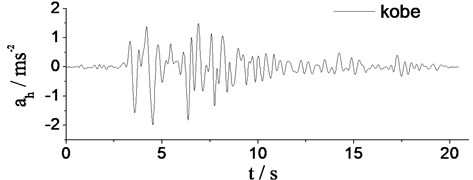
The geogrid thickness is 3 mm. The geogrid is a high density polyethylene (HDPE) and has only one direction (perforations is 38×1.5 cm, its static ultimate strength is 120 kN/m). A rigid connection is assumed between geogrids and walls. The schematic of the model dimension is shown in Fig. 1 and Fig. 2. A super load of 0.5 kPa is added to the surface of backfill soil to simulate an eternal load. A seismic waveform of Kobe in Japan is applied to simulate seismic load, 0.2 g, which is shown in Fig. 3.
Fig. 3Input seismic wave
2.2. Material properties
The backfill is sandy soil and the foundation is clayey soil. Mohr-Coulomb model is used to simulate the backfill and the foundation. The wall is the whole cast concrete panel. The constitutive model is an isotropic and elastic solid element. The stress-strain relationship meets linear Hooke’s law. represents shear modulus of soil; represents bulk modulus of soil; represents Poisson’s ratio. The formula is shown as Eq. (1) and Eq. (2). The parameters of the contact surface between geogrid and sand are shown in Table 1. represents cohesion; represents strength of extension; represents internal friction angle:
Table 1Calculation parameters of reinforced wall and soil
Material name | (kg/m3) | (MPa) | (MPa) | (kPa) | (MPa) | (°) |
Backfill | 1900 | 14 | 30 | 0 | 0 | 35 |
Foundation | 2000 | 18 | 40 | 15 | 0 | 30 |
Wall | 2400 | 2000 | 3000 | 7000 | 1 | 40 |
Table 2Parameters of geo-grid and interface model
(kg/m3) | (kN/m) | (GPa) | (mm) | (kPa) | (°) | (MPa) | |
1 | 120 | 1 | 0.3 | 2 | 2 | 30 | 2 |
Because the geogrid tensile strength and modulus ratio is relatively great, tensile curve is linear under small strain. And a large number of measurement and calculation results show that the pull force of geo-grid suffered in the backfill is far smaller than its tensile strength. Therefore, geo-grid material can be seen as isotropic linear elastic material without destruction limit.
There is a simulation element of geogrid in the program of FLAC3D. The element is usually used to simulate the flexible film which is described shear actions between geo-grid and soil. The interface characters between geogrid and soil are controlled by coupling elastic parameters. The ideal elastic-plastic model is applied to simulate the contact surface between soil and geogrid, to simulate the contact surface between soils and panels. The ideal elastic-plastic model meets the Mohr-Coulomb criterion and the tensile strength criteria. The parameters of the contact surface model between geogrid and soil are shown in Table 2. represents elastic modulus; represents coupling elastic cohesive. is the friction angle of the coupling spring, is the stiffness of per unit area and is the thickness of geogrid.
2.3. Boundary conditions
A free boundary is used in dynamic analysis. Boundaries of each side of the simulated model are considered as free-field motion without geo-structure. The free boundaries are achieved by generating two-dimensional and one-dimensional grids around the simulation model in the program of FLAC3D. An unbalanced force of the free field is applied to simulate the main grid boundaries. In FLAC3D, boundary models of free fields include four-plane grids and four-column grids. The plane grids on the boundary correspond to the main grids. The column grids are equivalent to free boundaries of free fields of plane grids. Plane grids of free fields are calculated as two dimensions and are assumed to be infinite on the normal plane. Column grids of free fields are calculated as one dimension and are assumed to be unlimitedly extended towards the ends of the cylinder.
2.4. Analysis conditions
In order to study seismic characters of geogrid reinforced soil retaining walls, some influence parameters are considered such as reinforcement length (), Geo-grid stiffness (), reinforcement spacing (), distribution form of reinforcement section, seismic strength , modulus of foundation and backfill, panel thickness (), the panel density () and so on.
The basic analysis condition is: equals to 0.7 times of the height ( is the height of a reinforced wall), is 0.1 g, equals to /10, is 1 GPa, is 0.24 H and is 28 MPa. Previous papers have reported the impact of the earthquake strength and reinforcement length. Research conditions in the paper are following as: geogrid stiffness (0.2 GPa, 0.6 GPa, 1 GPa, 2 GPa); panel thickness 0.03 H, 0.04 H, 0.05 H or 0.06 H); panel density (18 kN/m3, 20 kN/m3, 24 kN/m3 or 26 kN/m3). Distribution forms of reinforcement section are as follows: equal length up and down, the middle part is longer than up and down part, up part is shorter than down part, and up part is longer than down part.
3. Seismic characteristics of reinforced walls
3.1. Residual deformations and reinforced internal forces
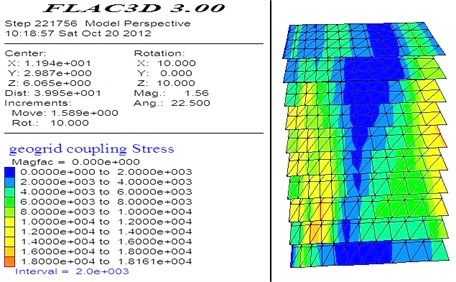
The deformation and stress nephogram of the geogrid reinforced soil retaining walls with integral panel under basic calculation conditions are respectively shown in Fig. 4 and Fig. 5. The lateral deformation of the wall top is in the maximum and is in the inclining deformation state outwards. The deformation along the wall decreases from top to bottom gradually. The vertical stresses in the root of the wall and the bottom of the foundation are relatively greater. The internal force nephogram of geo-grid in the reinforced zone are shown in Fig. 6. In the whole, the stresses in the up and bottom zone are relatively smaller, and those in the middle and lower part are relatively greater. The coupling shear stresses in the interface of every geo-grid layer are small in the middle of geo-grid and great in the end of geo-grid.
Fig. 4Residual deformation nephogram
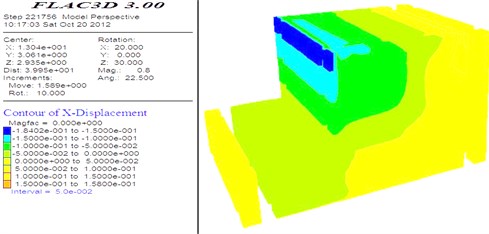
Fig. 5Vertical stress nephogram
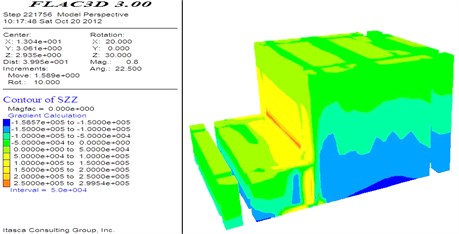
Fig. 6Shear stress nephogram of geogrid layers
3.2. Impacts of reinforcement spacing
Fig. 7(a) shows the distribution of maximum internal force ratio () of geogrid layers along the height of reinforced walls. Fig. 7(b) shows the time curve of the lateral deformation of the wall top under earthquake. The distribution characters of reinforced internal forces along wall heights are consistent under the impact of different reinforcement spacing. Reinforced internal forces increase with the increase of wall depth. When the depth of the reinforced wall is about 0.7 times of the whole wall height, reinforced internal forces increase the maximum, and then gradually decrease. The smaller the reinforcement spacing is, reinforced internal force is smaller and the residual deformation of reinforced wall is smaller. When the reinforcement spacing is reduced from 7.5 to 10, the reinforced internal forces of geogrid layers and the residual deformations of walls decrease slightly. Therefore, in seismic designs, an ideal reinforcement spacing of geogrid reinforced soil retaining walls is about 7.5.
Fig. 7Distribution of internal force of geogrid along wall and lateral deformation under different reinforced spacing
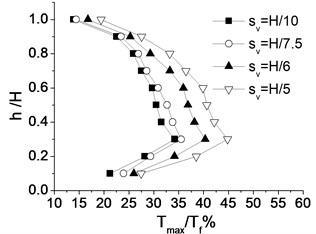
a) Reinforced internal force distributions of geogrid layers
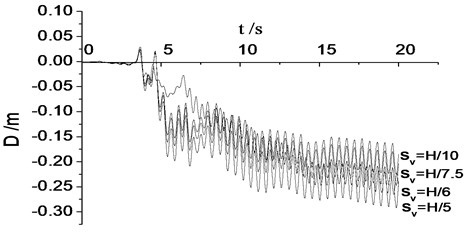
b) Time curve of the lateral deformation
3.3. Impacts of reinforcement lengths
Fig. 8 shows the distribution of maximum internal force ratio of each geogrid layer along the height of reinforced walls under different reinforcement length (). The distribution characters of reinforced internal forces along wall heights are consistent under the impact of different reinforcement length. Reinforced internal forces also increase with the increase of wall depth. When the depth of the reinforced wall is also about 0.7 times of the whole wall height, the reinforced internal forces increase the maximum, and then gradually decrease. The longer the reinforcement length is, the smaller the reinforced internal force is. When the reinforcement length increases from 1.0 to 1.2, the reinforced internal force decreases relatively less. Hence, an ideal reinforcement length is considered as 1.0 in seismic designs.
3.4. Impacts of geogrid distribution forms
Fig. 9 gives the distribution of maximum internal force ratio of every geo-grid layer along the reinforcement height under different distribution forms of geo-grid. As is shown in the figure, when the upper and lower length is equal, the internal force is in the minimum, and it is the most ideal distribution form. And the distribution form that the upper and lower part is short and the middle part is long is also a relatively ideal distribution.
Fig. 8Distribution of internal force of geo-grid along wall under different reinforced length
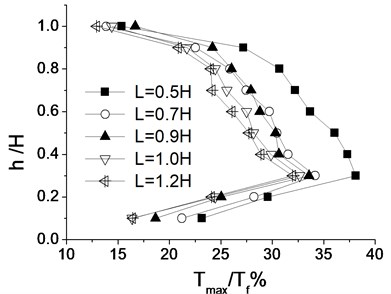
Fig. 9Distribution of internal force of geo-grid along wall under different reinforced style
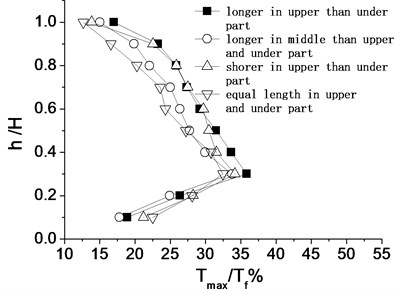
3.5. Impacts of geogrid stiffness
Fig. 10 shows the distribution of maximum internal force ratio along the wall under different geo-grid stiffness. As is shown in the picture, the internal force distribution along the wall is consistent under different geo-grid stiffness , and the distribution law is the same as the above. The greater the geo-grid stiffness is, the smaller the residual deformation is. So, geo-grid stiffness is a significant influence factor on the seismic characteristics of the retaining wall.
3.6. Properties of soils
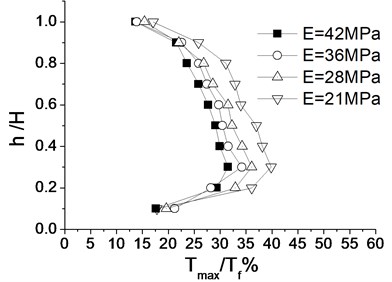
Fig. 11 shows the distribution characters of the maximum reinforced internal force ratio along the height of the reinforced wall under different soil modulus. The distribution characters are consistent under different soil modulus and are the same as the above design parameters. The larger elastic modulus of soils is, the smaller reinforced internal force is. When the elastic modulus of soil is larger than 36 MPa, the reinforced internal force decreases relatively less. Hence, in seismic designs, the soil modulus of 35 MPa is relative more suitable.
Fig. 10Distribution of internal force of geo-grid along wall under different reinforced stiffness
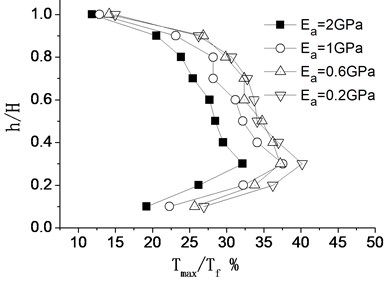
Fig. 11Distribution of reinforced internal force under different soil properties
3.7. Impacts of seismic intensities
Fig. 12 gives the distribution along the wall of the maximum internal force ratio under different earthquake intensity and deformation time curve. As is shown in the picture, reinforcement internal force distribution is consistent under different earthquake intensity. The distribution law is the same as the above. The earthquake intensity is a significant factor, and the higher the intensity is, the greater the internal force is.
Fig. 12Distribution of internal force of geo-grid along wall and lateral deformation under different earthquake intensity
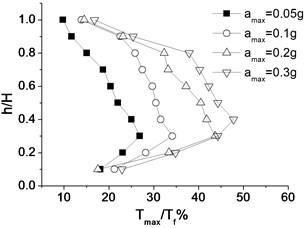
a) Distribution of the reinforcement layers
b) Time curve of the lateral deformation
3.8. Impact of panel density
Fig. 13 gives the distribution of the maximum internal force ratio along the wall under different panel density . As is shown in the picture, the internal force distribution along the wall is consistent under different panel density. But it is obvious that panel density has little effect on the internal force of geo-grid. As a result, panel density is not a key factor in seismic design of the reinforced structure.
3.9. Impacts of wall thicknesses
Fig. 14 (a) shows distribution characters of maximum reinforced internal force ratio under different panel thicknesses () along the heights of reinforced walls. Fig. 14(b) is the distribution characters of seismic residual deformations of reinforced walls. The distribution characters of reinforced internal forces are consistent and seismic residual deformations of walls under different thicknesses of panels. The thicker the reinforced wall is, the reinforced internal force is smaller and the smaller the residual deformation is as well. When the thicknesses of the reinforced walls increase from to seismic residual deformations of reinforced walls decrease minimal slightly. Hence, 0.05 can be considered as a suitable thickness of panels in seismic designs of geogrid reinforced soil retaining walls.
Fig. 13Distribution of internal force of geo-grid along wall under different unit weight of wall
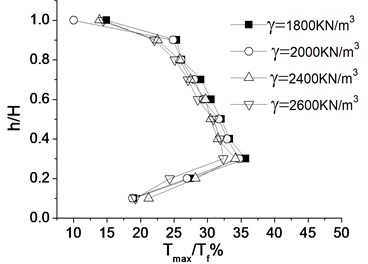
Fig. 14Distributions of residual deformations and reinforced internal forces under different wall thicknesses
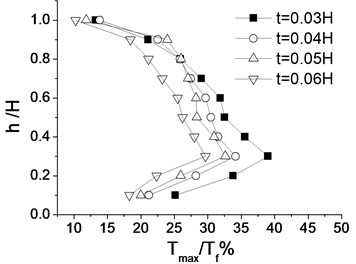
a) Maximum reinforced internal force ratio of geogrid layers
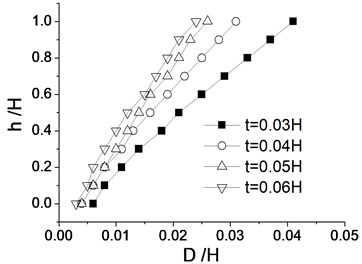
b) Distributions of seismic residual deformations of reinforced walls
4. Shaking table test on seismic strains of geogrids
4.1. Test model
The self-developed large-scale shaking table test model and test results of seismic strains of geogrid layers of geogrid reinforced soil retaining wall are taken in the paper. The test is conducted by the self-developed 15-layers laminated shear model soil box, and the size of the box is 3.5 m (lengthwise direction) × 2.0 m (cross direction) × 1.7 m (vertical direction). The time similarity ratio is 0.5. The size of the reinforced retaining wall used in the test is 70 (height) × 5 cm (width). The groundwater level is 5 cm below the ground surface. At the bottom of the base is clay, which is 50 cm thick and to reduce water penetration of the backfill sand. The material of wall in the test model is mainly made up of low intensity concrete and a grade reinforced bar. The unit weight of the wall model is 19 kN/m3. The strength of geogrids is relatively low. When the extensibility of the type of geogrid reaches 2 %, the pulling force of the reinforced geogrid is 14 kN/m. The reinforcement spacing is 15 cm and the reinforcement length is 70 cm, which is the same as wall height. The backfill sand is Nanjing fine sand and is prepared by submerging in water. A relative density of 55 % is controlled. The viscosity of the pore water in the model is consistent with the pore water in a prototype. The average particle diameter D50 is 0.15 mm, and permeability coefficient of sand is 5.5×10-5 m/s.
4.2. Test setup and working conditions
Fig. 15 shows the test equipment and instruments of the reinforced soil retaining wall model, in which 83 signal acquisition channels were taken in total. Five horizontal accelerometers are placed into the reinforced backfill sand (A1-1~A1-5), and three horizontal accelerometers are placed into the unreinforced zone (A2-1, A2-3 and A2-5), and three accelerometers are installed onto the wall surface (A3-1, A3-3 and A3-5). Three laser displacement meters (DH1~DH3) are installed onto one batten fixed by one steel frame to test the lateral displacements of walls. Two laser displacement meters (DV1 and DV2) are installed onto battens to record the settlements of the backfill sand surfaces of the reinforced zone and the unreinforced zone. Eight pore pressure meters are placed into the backfill sand to test excess pore water pressures, five of which are placed into the reinforced zone (W1-1~W1-5), three of which are placed into the unreinforced zone (W2-1, W2-3 and W2-5). Forty strain gauges are pasted onto the geogrid surface, and each layer is pasted both positive and negative surfaces and 4 strain gauges are pasted onto each surface to test the seismic strain of geogrid.
Fig. 15Shaking table test model of geo-grid reinforced soil retaining wall (model dimensions: cm)
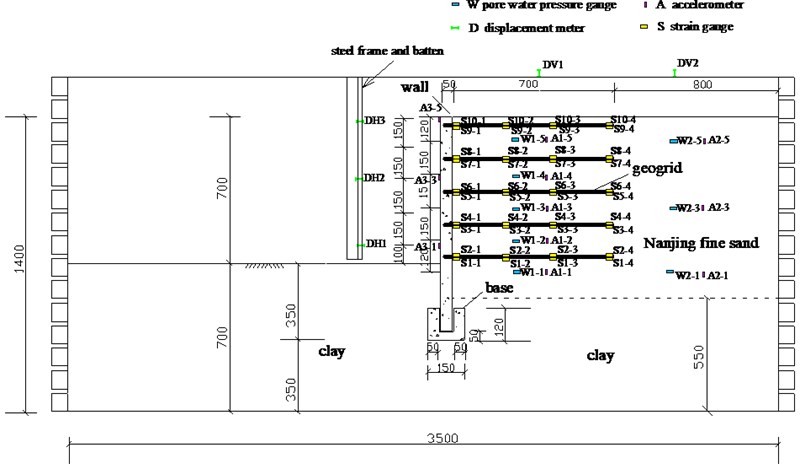
Fig. 16Input earthquake acceleration motion and spectrum in Songpan
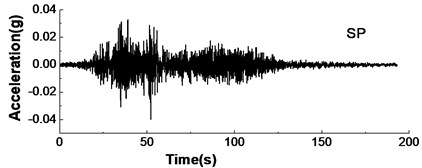
a) Acceleration time history
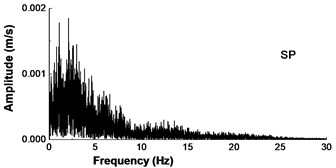
b) Fourier spectrum
According to the test purpose, by considering the earthquake wave characters, white noise signal, 5.12 Wenchuan earthquake records and Taft earthquake records are chosen as external stimulus. In this paper, the test results under Songpan wave in Wenchuan earthquake are applied to study the strain response characteristics of geo-grid. The original peak acceleration of Songpan wave is 0.041 g, and fault distance is 122 km. Hence, Songpan wave belongs to far-field vibration, and its seismic waveform is shown in Fig. 16. The excitation points driven by the shaker table are on the bottom of the test model box. The excitation intensities are respectively 0.2 g, 0.3 g and 0.5 g, which are called respectively SP-1, SP-2 and SP-3.
4.3. Seismic strains of geogrids
Fig. 17 shows time histories of dynamic strain response of geogrid under the seismic wave of SP-2 (0.3 g). Fig. (a)-(c) show the strain characteristics of geo-grids, which are respectively located in the bottom layer, the middle layer and the top layer of the middle reinforced zone (S1-2, S5-2 and S9-2). According to the figures, it can be achieved that the geogrid strain at the bottom of reinforced zone is the smallest, and that at the top of reinforced zone is also small, but, the strain in the middle of reinforced zone is the largest. These results show that internal force of geo-grid at the bottom of reinforced zone is small and its effect for the seismic capacity of reinforced wall is very weak, and that internal force of geogrid in the middle of reinforced zone is the largest and its effect for the seismic capacity of reinforced wall is very strong.
Fig. 17Time histories of geogrid strains on different reinforced layers
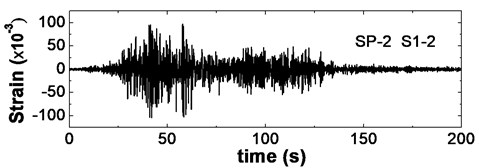
a) Bottom layer
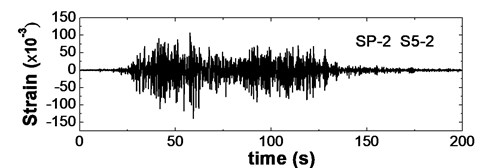
b) Middle layer
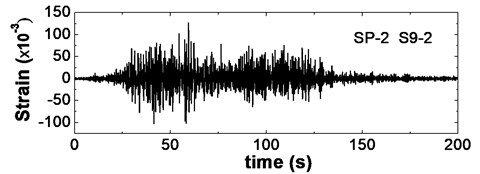
c) Top layer
Fig. 18 compares the distribution characters of strain amplitudes of geogrid roots (S1-1, S3-1, S5-1, S7-1 and S9-1) along the wall height ratio () under the effects of different seismic intensities. The higher the seismic intensities are, the greater the geogrid strains are. Test results and numerical simulation results are basically consistent, which both show that the geogrids located in the middle of the reinforced zone play an important role for the seismic stability of geogrid reinforced soil retaining wall.
Fig. 18Strain amplitude distributions of geogrid roots along wall heights under different seismic intensities
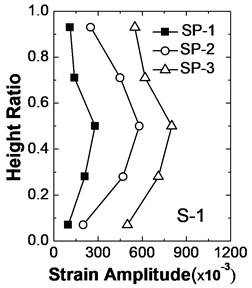
5. Conclusions
A finite difference method was applied to study the seismic distribution characters of reinforced internal forces of geogrids under different parameters, and a large-scale shaking table test is also applied to study the dynamic strain of geogrids in reinforced zone. Some conclusions are as follows:
1) The reinforced wall is in inclined deformation state outwards, and the residual deformation at the top of wall is the largest. The coupling shear stresses on the interface between geogrids and soils are smaller in the middle of geogrid layers and larger in two ends of geogrid layers. The reinforced stresses of geogrids located on upper layers and bottom layers are relative smaller. The reinforced stresses of geogrids located in the middle layers are relatively larger.
2) The reinforced internal forces of geogrids decrease with the decrease of the reinforcement spacing. The ideal reinforcement spacing can be thought as /7.5 in seismic designs. The reinforced internal forces of geogrids decrease with the increase of the reinforcement length. The ideal reinforcement length can be valued as 1.0 H in seismic designs.
3) Equal length of up and down part along reinforced zone depth is the best distribution form for geo-grid, and the internal force is the smallest. Geo-grid stiffness is a very significant effect factor for the seismic internal force of geogrids.
4) The panel density has little effect on the seismic internal force of geo-grid. It isn’t a key factor in the seismic design of the reinforced structure. The reinforced internal forces of geogrid layers decrease with the increase of the panel thickness. An ideal thickness of the reinforced panel is 0.05 in the seismic design of geo-grid reinforced wall.
5) Modulus of foundation and backfill soil has significant impact on the seismic internal force, and when the modulus is large, the internal force is small. When the soil modulus is 35 MPa, the seismic resistance ability of reinforced walls is the best.
6) Results from shaking table test show that reinforcement internal forces of geogrid located in the middle part of the reinforced zone are the largest. Test results and numerical simulation results both show that the geogrids located in the middle layer of reinforced zone play an important role. The above achieved conclusions can provide references for the seismic design of geo-grid reinforced soil retaining wall.
References
-
Huang, C. C. Investigations of soil retaining structures damaged during the Chi-Chi earthquake. Journal of the Chinese Institute of Engineers, Vol. 23, Issue 4, 2000, p. 417-428.
-
Race R., Del Cid. H. Seismic performance of modular block retaining wall structures during the January 2001 El Salvador earthquake. Proceedings of the International Geosynthetic Engineering Forum, Taipei, Taiwan, 2001.
-
Yang Guang-qing, Lu Peng, Zhang Baoxian, Zhou Qiaoyong Research on geogrids reinfoced soil retaining wall with concrete rigid face by field test. Journal of Rock Mechanic and engineering, Vol. 24, Issue 14, 2005, p. 2428-2433, (in Chinese).
-
Andrzej Sawicki Creep of geosynthetic reinforced soil retaining walls. Geotextiles and Geomembranes, Vol. 17, Issue 1, 1999, p. 51-56.
-
Deepankar Choudhury, Syed Mohd. Ahmad Pseudo-static design factors for stability of waterfront-retaining wall during earthquake. Earthquake and Tsunami, Vol. 4, 2010, p. 387-395.
-
Chia-Cheng Fan Three-dimensional behaviour of a reinforced earth-retaining structure within a valley. Computers and Geotechnics, Vol. 33, Issue 1, 2006, p. 69-85.
-
Assaf Klar, Tal Sas The KC method: numerical investigation of a new analysis method for reinforced soil walls. Computers and Geotechnics, Vol. 37, Issue 1, 2010, p. 351-358.
-
Huei-Tsyr Chen, Wen-Yi Huang, Chin-Chang Chang, Yuan-Ji Chen, Chung-Jung Lee Centrifuge modeling test of a geotextile-reinforced wall with a very wet clayey backfill. Geotextiles and Geomembranes, Vol. 25, Issue 6, 2007, p. 346-359.
-
Lee K. Z. Z., Chang N. Y., Ko H. Y. Numerical simulation of geosynthetic-reinforced soil walls under seismic shaking. Geotextiles and Geomembranes, Vol. 28, Issue 4, 2010, p. 317-334.
-
Izawa J., Kuwano J. Centrifuge shaking table tests on saturated reinforced soil walls. Proceedings of the 4th Asian Regional Conference on Geosynthetics, Shanghai, China, 2008.
-
Nicola Moraci, Giuseppe Cardile Deformative behaviour of different geogrids embedded in a granular soil under monotonic and cyclic pullout loads. Geotextiles and Geomembranes, Vol. 32, Issue 3, 2012, p. 104-110.
About this article
The authors appreciate the support of National Natural Science Foundation of China (No. 51109099) and National Science Foundation for Post-doctoral Scientists of China (No. 2011M50906).
