Vibration suppression using fractional-order disturbance observer based adaptive grey predictive controller

2.1. Grey predictive control structure

Grey predictive control strategy is designed based on the control decision made on the basis of system future behavioral tendency, and the grey predicted outputs could always provide us some useful information for better control of the system before the system behavior runs into bad situations [16]. The control structure is depicted in Fig. 1.

Fig. 1Grey predictive control structure

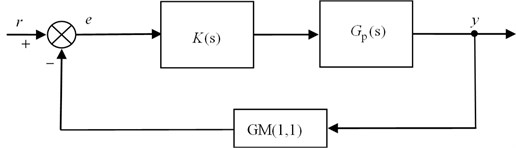
In Fig. 1, $G_p\left(s\right)$ is plant transfer function, $K\left(s\right)$ is the regulator, and it can take PID or other control modes, GM(1,1) module is the grey prediction module. Signals $r$, $y$, $e$ denote the reference input, system output and tracking error respectively. Let $\mathbf{Y}=\left\{y\right(k),k=1,2,\dots ,n\}$ stand for a sample of the output components with $y\left(k\right)$ being the output at time $k$. And via translational processing, we can obtain a positive sequence ${\mathbf{Y}}^{\left(0\right)}=\left\{y^{\left(0\right)}\right(k),k=1,2,\dots ,n\}$. Then GM(1,1) model could be constructed with the positive sequence ${\mathbf{Y}}^{\left(0\right)}$ by the following basic steps [17].

First, apply a preliminary transformation called accumulated generating operation (AGO) to reduce the noise of ${\mathbf{Y}}^{\left(0\right)}$ and to get a new monotonically increasing data sequence ${\mathbf{Y}}^{\left(1\right)}=\left\{y^{\left(1\right)}\right(k\left)\right|y^{\left(1\right)}\left(k\right)=\sum _{i=1}^k{y}^{\left(0\right)}\left(i\right),k=1,2,\dots ,n\}$. Then the grey differential equation can be formed as follows:

where $z^{\left(1\right)}\left(k\right)=0.5\left[y^{\left(1\right)}\right(k)+y^{\left(1\right)}(k-1\left)\right]$, $a$ is developing coefficient and $b$ is the grey input.

Adopt least square method to estimate the model parameters ${\left[ab\right]}^T$:

where $\mathbf{B}$, ${\mathbf{Y}}_N$ are the data matrix and data vector respectively:

White-formed ordinary differential equation of grey model GM(1,1) is:

Solve Eq. (3) with the obtained model parameters ${\left[ab\right]}^T$ and apply the inverse AGO (IAGO) to figure out predictive values:

where $\xi$ is prediction step.

Finally, via inverse translational processing, we can obtain the predictive system output $\widehat{y}(n+\xi )$ which will be sent to the controller. In a grey predictive control system, predictions are often done using metabolic models. Thus, the parameters of the prediction device vary with time, and this would guarantee a strong adaptability of the system.

2.2. Disturbance observer

As is well-known, the performance of the closed-loop system will degrade in the presence of external disturbances, and in order to enhance the disturbance rejection performance of system, the DOB is introduced [14]. DOB is located inside the control closed-loop, and it can further reduce the influence of vibration and model perturbation on the basis of closed-loop regulation. The basic idea of DOB is to use a nominal model of the plant to estimate the disturbance caused by outer interference torque and parameter variation, and an equivalent compensation action is generated from the estimate [8]. The architecture of DOB is depicted in Fig. 2, where $G_n^{-1}\left(s\right)$ is the inverse of nominal model, $Q\left(s\right)$ is a low-pass filter, and $d$ is the equivalent disturbance. The relative order of $G_n\left(s\right)$ is usually not equal to zero, and this leads to that the inverse $G_n^{-1}\left(s\right)$ cannot be realized physically. Thus $Q$-filter is introduced to solve the problem in DOB.

Fig. 2Block diagram of DOB

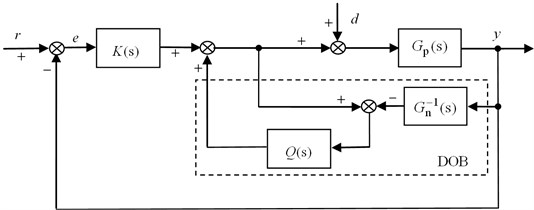
In Fig. 2, system output $y$ can be calculated by:

Assumption 1. The closed-loop system is stabilized by $K\left(s\right)$, and the disturbance $d$ has a bounded steady-state value, i.e., the value satisfies the equation $\underset{t\to \infty }{\mathrm{l}\mathrm{i}\mathrm{m}}d\left(t\right)=\underset{s\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}sD\left(\text{s}\right)<\infty$ [14].

Assumption 2. The $Q$-filter in DOB is an ideal low-pass filter with a cutoff frequency $w_q$, it means that when $w<w_{\text{q}}$, $Q\left(\text{s}\right)\approx \text{1}$, and when $w>w_{\text{q}}$, $Q\left(\text{s}\right)\approx \text{0}$.

Now, with the above two assumptions, Eq. (5) can be approximated as:

From Eqs. (5) and (6) we can find that, DOB can effectively suppress the external disturbance, and make system characteristic approximately equal to nominal model.

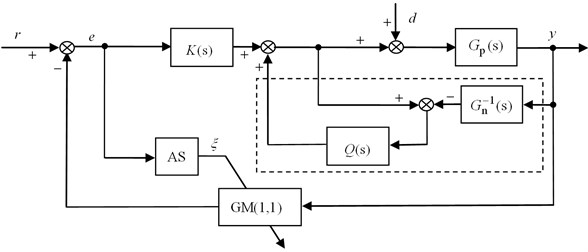
3.1. Adaptive step switching module

In general, when system tracking error $e$ is large, the controller should transmit a big control signal to speed up the system response and result in a shorter settling time. And when the system error is small, the controller should generate a smaller control signal to prevent the system overshoot. Thus, for obtaining an excellent system control performance, we use the following switching mechanism in AGPC to determine prediction step size which would affect the generated control signal [18]:

where $e_s$ and $e_l$ are the switching values, ${\xi }_1$, ${\xi }_2$, and ${\xi }_3$ are the step sizes for the large error, the middle error and the small error respectively. The negative-step can increase the upward momentum of the output curve for shortening the settling time, and appropriate positive-steps can be used to prevent the overshooting.

3.2. Fractional order $\mathit{Q}$-filter design

The design of $Q$-filter is an important step when applying DOB, and $Q$-filter characterizes the overall performance of the designed DOB. If given the required cutoff frequency of $Q$-filter, it turns out that the relative degree is the major turning knob for the tradeoff between stability margin loss and vibration suppression [7]. Conventional DOB chooses the relative degree just in integer domain, and in order to further improve vibration suppression performance while keep enough stability margin, the filter order can be expanded to real-number domain. The fractional order version of $Q$-filter is:

where $\tau$ is the filter time constant and $\alpha$ is the relative degree of $Q$-filter. For implementation of the fractional order $Q$-filter, proper approximation by finite difference equation is needed. In this study, the broken-line approximation method is introduced to approximate $1/{(\tau \text{s}+1)}^{\alpha }$ in frequency range $[w_b,\hspace{0.17em}{w}_h]$, where $w_{\text{b}}=1/\tau$, $w_{\text{h}}$ is taken as 10⁴ to give an enough frequency range [15]. Let:

Eq. (9) can be approximated with the approach of cascading rational functions, and there is:

where:

Fig. 4Bode plots of ideal case and its approximations

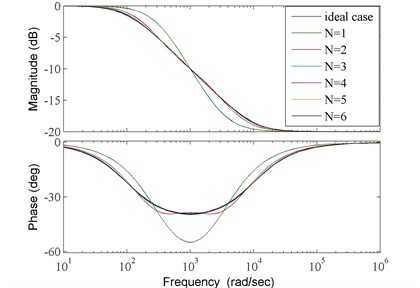
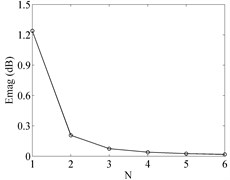
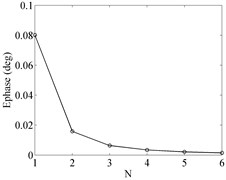
The bigger approximation order $N$ is, the higher approximation accuracy is. But when $N$ reaches a certain value, approximation accuracy would not be proportionally increased [19]. Take $\alpha =\text{0.5}$, $w_b=\text{100}$, $w_h={\text{10}}^{\text{4}}$ as a case study, the Bode plots of ideal case and its approximations with $N=$1, 2, 3, 4, 5, 6 are shown in Fig. 4. And we can find that big approximation error only exists in the approximation with $N=\text{1}$.

For further showing the differences in approximations with different orders, the mean absolute errors of frequency characteristics between ideal case and its approximations are employed as accuracy evaluation standards, they are defined as follows:

where $E_{mag}$, $E_{phase}$ are the mean absolute errors of amplitude-frequency characteristic and phase-frequency characteristic respectively, $w_0=w_b$, $w_m=w_h$.

The evaluation results shown in Fig. 5 indicate that, the improvement of approximation accuracy is slight when approximation order is bigger than 4. Thus, 4th-order broken-line approximation for fractional order $Q$-filters would be adopted in this study.

Fig. 5Evaluation results of approximations with different orders

a)

b)

4.1. Example 1

First, examine system responses to a step signal while there is a disturbance $d=2+0.5\mathrm{s}\mathrm{i}\mathrm{n}\left(0.1\pi t\right)$ existing in system. Three kinds of controllers are used to regulate the system separately, they are proportional controller $K_n=\text{2}$, adaptive grey predictive controller (AGPC), and the newly proposed controller, fractional-order disturbance observer based adaptive grey predictive controller (FDOB-AGPC). The feedback regulators in AGPC and FDOB-AGPC both employ proportional controller $K_n=\text{2}$. And in grey prediction module, the number of prediction sequence is 4. Since grey prediction model has a relatively high accuracy for short-term forecasting, we take the maximum prediction step is 4. Via comparing, the dynamic prediction mode performs the big positive-step step ${\xi }_3=\text{4}$, small positive-step ${\xi }_2=\text{1}$ and negative-step ${\xi }_1=$–3 mode based on the tracking error $e$. Thus the switching mechanism is defined as follows:

Eq. (15) indicates that fractional order $\alpha$ of $Q$-filter should be not less than 2, and to prevent the system from becoming too complex, we take $\alpha =\text{2.0,\hspace{0.17em}2.2,\hspace{0.17em}2.4,\hspace{0.17em}2.6,}\text{2.8,\hspace{0.17em}3.0}$ to study. Bode curves of $Q$-filter with different $\alpha$, $N=\text{4}$, and approximation bandwidth [100, 10000], are shown in Fig. 6. From Fig. 6 we can see that, changing the $Q$-filter’s order fractionally can effectively enlarge the range of control system’s frequency responses adjustment than just turning it among integer orders.

Fig. 6Bode curves of Q-filter with different α

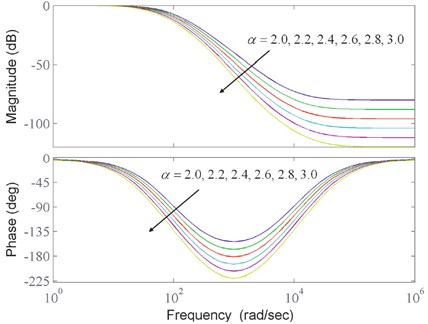
Fig. 7System responses to the step signal with different controllers

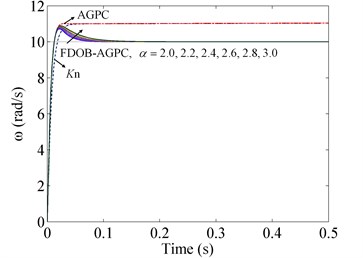
a) Response curves

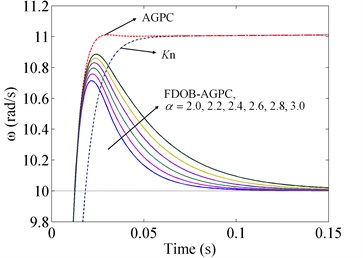
b) Partial enlarged curves

System responses to the step signal with different controllers are depicted in Fig. 7. Via comparing the curve of AGPC with that of proportional controller, we can see that AGPC with adaptive steps can improve the response speed remarkably. But the two controllers both have steady-state errors because of the external disturbances, it means that they have poor suppression abilities for external disturbances. Whereas, the steady-state error no longer exists in the response curves of FDOB-AGPC, this implies FDOB-AGPC can give better vibration suppression performance with the help of FDOB. While the control system still keeps stable, the bigger fractional order $\alpha$ is, the more deteriorative the performance is. Since larger $\alpha$ gives more phase margin, simulation results verify a tradeoff between stability and the strength of vibration suppression exists. In addition, responses of FDOB-AGPC with different $\alpha$ indicate that fractional order can provide a wider adjustment range than integer order, and can make the adjustment alter continuously.

4.2. Example 2

To simulate the actual system truthfully, friction torque is used as the equivalent disturbance $d\text{,}$ and considering that plant $G_p\left(s\right)$ contains an multiplicative perturbation $G_P\left(s\right)=G_n\left(s\right)+\mathrm{\Delta }P\left(s\right)$, $\mathrm{\Delta }P\left(s\right)=-0.1G_n\left(s\right)$. In this example, the aggregate friction model which is composed of static friction, Coulomb friction, viscous friction and Stribeck friction is employed. The friction moment can be defined as follows [20]:

where $\dot{\theta }$ is motor speed, $\delta \left(\dot{\theta }\right)$ is switching function, and $M_{static}$, $M_{slide}$ are static friction moment and sliding friction moment respectively:

where $M\left(t\right)=J\ddot{\theta }$ is driving torque, $M_m$ is maximal static friction moment, $M_c$ is Coulomb friction moment, $k_{\text{v}}$ is proportional coefficient of viscous friction moment, ${\alpha }_1$ and $\alpha$ are both small constants. And in this study, there are $M_m=\text{0.6}\text{Nm}\text{,}$$M_{\text{c}}=\text{0.5}\text{Nm}\text{,}$${\alpha }_1=\alpha =\text{0.01}\text{,}$$k_v=\text{0.04}$.

Fig. 8Friction torque curves

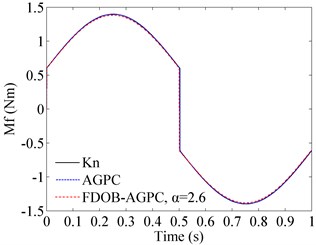
Take sinusoidal signal $r=20\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi t\right)$ as reference input, and still employ the above three kinds of controllers to regulate the system. Except $K_n=\text{12}$ and $\alpha =\text{2.6}$, other configurations for these controllers are not changed. Friction torque curves are shown in Fig. 8, and system responses to the sinusoidal signal are depicted in Fig. 9.

Tracking curves in Fig. 9 illustrate that steady-state errors still exist when applying proportional controller and AGPC. As friction torques suddenly change at zero-crossing points of motor speed, mutations appear in the tracking processes as depicted in error curves. The sudden change of friction torque also has adverse influence on FDOB-AGPC, but FDOB-AGPC can adjust quickly, and its steady-state error is no more than 0.1 rad/s with the compensation action of FDOB. Thus, the results validate that when FDOB is introduced, the system has better robust stability.

Fig. 9Tracking abilities of sinusoidal signal with different controllers

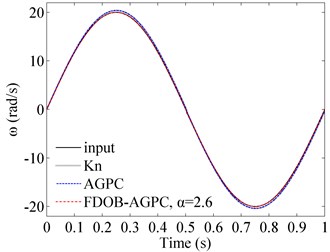
a) Tracking curves

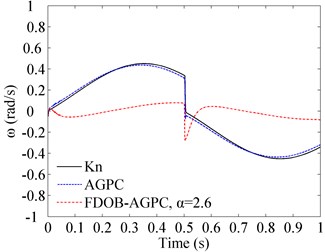
b) Error curves

4.3. Example 3

For the same simulation conditions described in Example 2, we consider tracking a more complex signal to validate the effectiveness of the newly proposed controller. The reference input contains three processes, acceleration process, uniform process and rapid deceleration process. Tracking results of the three controllers are shown in Fig. 10.

Fig. 10Tracking abilities of a more complex signal

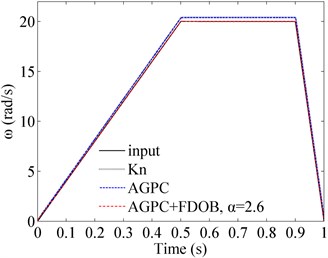
a) Tracking curves

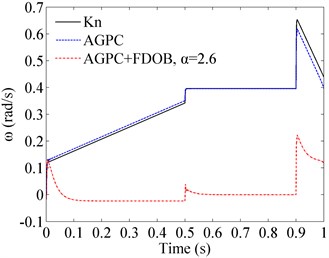
b) Error curves

During the acceleration process, tracking errors of proportional controller and AGPC increase as the friction torques become bigger which are determined by the motor speed. From the uniform process we can see that, steady-state errors always exit when applying proportional controller and AGPC. And the relatively large deceleration brings worse impacts on the two controllers. The large deceleration also has adverse influence on FDOB-AGPC, but throughout the control process of FDOB-AGPC, big tracking errors mainly occur at the state transition points, and the biggest error is only 0.2229 rad/s. Comparing with proportional controller and AGPC, the overall control performance of FDOB-AGPC is encouraging. And the simulation results of this example is concordant with the ones of Example 2.