Abstract
The high-performance application of high-power permanent magnet synchronous motor (PMSM) is increasing. This paper focuses on the parameter estimation of PMSM. A novel estimation algorithm for PMSM’s dual-rate sampled-data system has been developed. A polynomial transformation technique is employed to derive a mathematical model for PMSM’s dual-rate sampled-data system. The proposed modified stochastic gradient algorithm gets more excellent convergence performance for smaller index . Simulation and experimental results demonstrate the effectiveness and performance improvement of the proposed algorithm.
1. Introduction
Permanent magnet synchronous motor (PMSM) are now widely employed in industrial servo drives, electric/hybrid electric vehicles, wind power generators, etc., due to their high power/torque density, high efficiency, and excellent control performance. And then, high performance control of PMSM drives requires accurate knowledge of the machine parameters. Often, the online estimation of parameters is required, and the control algorithm can use updated parameter information and modify the controller behavior accordingly. It is important to obtain accurate machine parameters for fault detection rotor/stator temperature monitoring, as well as for achieving high control performance. Many methods have been proposed to obtain the parameters with different online estimation strategies from the measured terminal signals, such as recursive least squares (RLS) [1-3], extended Kalman filter (EKF) [4, 5], neural network (NN) [6-8] and the model reference adaptive system (MARS) [9, 10].
To the aforementioned methods, the input and output channel of discrete-time systems have the same updating and sampling period in general. A high updating and sampling frequency therefore enables the acquisition of better accuracy to estimation strategies. On the other hand, sampling period has limitations relating to hardware performances. Furthermore, sometimes, it is unrealistic to sample all variables in a complex system with a single frequency. Multirate systems arise when several sampling and updating rates co-exist in a system, due to some practical limitations [11, 12]. The identification of multirate systems has received much attention in past decade, because many practical applications in industry can be found [13]. It is the first step of parameter estimation to develop an appropriate model structure that is consistent with all different input/output sampling rates. Generally, there are two main methods to transform the multirate model: lifting technique [16] and polynomial transformation technique [11, 17-19]. With the two model transformation techniques, existing methods for multirate system parameters estimation include sub-space algorithms [17, 19], stochastic gradient (SG) algorithms [19, 20], and least squares (LS) methods [11]. Ding and Chen [21] presented a stochastic gradient algorithms based on the auxiliary models for dual-rate systems to estimate simultaneously the system parameters and the unknown inter sampling output. Ding et al. [20] presented a modified SG (MSG) algorithm with better convergence performance than SG for parameter estimation using the dual-rate input-output data. Li et al. [17] used the least squares algorithms to estimate parameters of the lifted state-space models. J. Ding and F. Ding proposed an LS algorithm to effectively identify systems parameters with noises [11].
In this paper, dual-rate system is defined as a special class of multirate system where the input is update data fast rate and the output is sample data slow rate; the two rates are related by an integer multiple. To PMSM electrical subsystem, “input” is defined as , , -axis reference voltages (in volts), measured for PI regulators, that is embedded in high performance microprocessor, such as FPGA or DSP. “Output” is then defined as , , actual -axis currents (in amperes), acquired with Hall current sensors and the microprocessor can get the output information by the A/D converter. Due to limitations of hardware, the sampling speed of the output (, ) is restricted to be slower than that of input (, ). And then, the sampling period for PMSM is selected so as to be equal to the longest of those two. On the other hand, sampling periods are set individually in multirate sampling control [22]. As a result, better performance can be acquired despite hardware limitations. Many studies have been performed on the system in which output information cannot be acquired fast enough, such as computer hard disk drives or visual servo systems [23-25].
The subject of this paper is the design of high performance estimation algorithm for PMSM’s dual-rate sampled-data system. We consider the design process to involve 1) setting up dual-rate model of PMSM, 2) developing a modified stochastic gradient algorithm, 3) analyzing the convergence of the proposed algorithm.
The rest of this paper is organized as follows. Section 2 discusses the PMSM model under dual-rate sampling. Based on this model, Section 3 proposes a novel parameter estimation algorithm for dual-rate systems. Section 4 and 5 provide the simulation and experimental validation, respectively. Section 6 summarizes the more important results of this paper.
2. Dual-rate model of PMSM
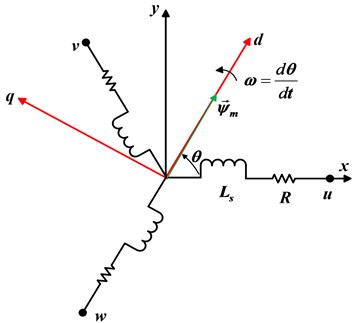
PMSM speed control is usually achieved using Park’s transformation. This method reduces the three-phase “” machine equations to a 2-D model. Fig. 1 shows the relationships among the two reference frames used in the speed control of the PMSM, i.e., the stator reference frame, and the reference frame corresponding to the real rotor (flux). Due to its simplicity, the linear model of the PMSM on the stator reference frame Eq. (1) is used in [26]:
where:
and , , are the stator voltage, stator current and permanent magnet flux space vectors, respectively. and denotes the stator resistance and inductance. and are the rotor speed and position in electrical degrees.
By transforming Eq. (1) into the coordinates, the linear model on the rotor reference frame is obtained as follows:
Subscripts and denote the components on the axes of the rotor reference frame. The model Eq. (2) can be rewritten in discrete time. The PMSM electrical state-space model is:
where:
and , , the superscript denotes the matrix transpose. is the sampling period.
Fig. 1Two reference frames used in speed control of PMSM
2.1. Polynomial transformation technique
In this paper, we focus on identification problems of PMSM’s dual-rate sampled-data systems. Fig. 2 shows the dual-rate sampling case, where is the zero-order hold with period converting the discrete-time signal into a continuous-time signal , is a sampler with period which samples continuous-time signal to yield a discrete-time signal , is a continuous-time process ( is an integer).
Fig. 2The dual-rate sampled-data system
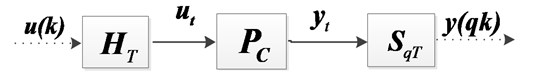
Assuming the continuous-time process is the linear time invariant system, the discrete-time model of can be described as:
where and are the system input and output, and are the unknown parameters, and is the known system order.
Let be the unit forward shift operator, and and be polynomials in :
Then Eq. (4) can be written into a compact form:
This model assumes that all input and output data are available. However, in the dual-rate sampled-data system, we can get all input data and scarce output data the intersample output or missing outputs are unavailable. We can use polynomial transformation technique [20] to derive the dual-rate model from Eq. (5).
Let the roots of be (), then:
Defining a polynomial with respect to :
Here, we have used the formula:
Multiplying both sides of Eq. (5) by yield:
or
with:
From Eq. (7), one can see that the model in Eq. (6) makes full use of all input-output data .
2.2. The model of PMSM with dual-rate sampling data
Here we take , , and assume , are input and output sampling period respectively. Exchange polynomial matrix can be expressed as:
PMSM discrete-time model Eq. (3) is multiplied by the polynomial matrix Eq. (8), the corresponding dual-rate mode of PMSM can then be expressed as:
For the simplification of the problem, we only take into account the -axis current that can then be expressed as:
where:
3. Proposed algorithm
We define parameter vector and input-output data vector as:
and then, with substituding , the model Eq. (10) can be transformed into regression form as:
where the superscript denotes the matrix transpose. In one output sampling period, we think the motor speed is constant, and then contains only the available measurement outputs and inputs.
Let be the estimate of at time . It is well known that the SG algorithm can estimate the parameter vector in Eq. (11) (the DR-SG algorithm for short) [20, 27]. However SG algorithm has a slower convergence rate compared with the recursive least squares (RLS) algorithm, but the SG algorithm require slower computation load, because RLS need compute the covariance matrix [11]. In order to improve the convergence rate and tracking performance of the DR-SG algorithm, we introduce a convergence index and present a modified stochastic gradient algorithm (the DR-MSG algorithm for short) for PMSM as follows:
where is the step-size and the norm of matrix is defined by The initial value is chosen to be a small vector, e.g., with being an -dimensional column vector whose elements are all 1.
4. Simulation results
In this section, we present simulation results to demonstrate the effectiveness of the proposed algorithm for PMSM system. The simulation environment is the Matlab/Simulink. The Simulink model of the PMSM parameters identification system with vector control, which includes parameters identification module, two current PI regulators and one speed PI regulator, has been constructed. The block diagram of the overall PMSM parameters estimation system is given in Fig. 3. The parameters of PMSM are given in Table 1. The motor speed response is given in Fig. 4. The simulation experiment includes two parts, i.e. the MSG identification for single-rate and dual-rate PMSM system.
Fig. 3The overall diagram of the PMSM parameters estimation system
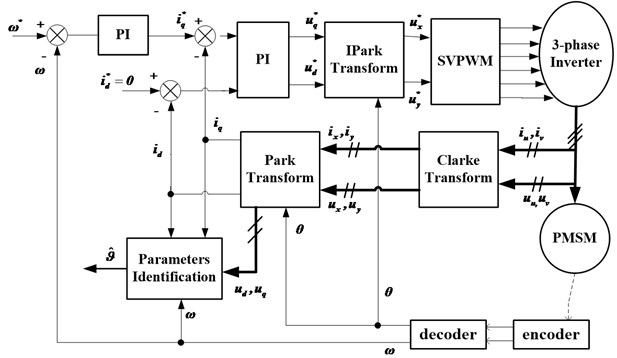
Fig. 4Speed response under ω*=100 (rad/s)
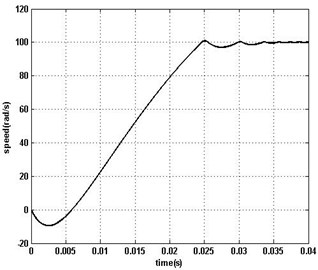
Table 1Machine parameters
Parameters | Value |
Stator resistance (Ohm) | 2.875 |
, -axis inductance (mH) | 8.5 |
Rotor inertia (kg/m2) | 0.0008 |
Permanent magnet flux (Wb) | 0.175 |
Number of pole pairs | 1 |
4.1. Parameters identification for single-rate system
In the subsection, simulation results have been obtained to verify the effectiveness of MSG algorithm for PMSM single-rate sampled-data system. PMSM system inputs and outputs () will be updated/sampled with period in Fig. 3.
From the PMSM discrete-time model Eq. (3), we assume parameter and input vectors as:
To quantify the identification accuracy, we define the estimation error as , measured in the Euclidean norm. The estimation results of applying the proposed MSG method with , , and in Fig. 4.
From Fig. 5(a), it is clearly observed that for smaller , the error is becoming smaller (in general) as time increases. Otherwise, when the value is smaller than 0.79, the convergence of MSG is becoming worse from Fig. 5(b). Furthermore, there is an optimal value to MSG algorithm for PMSM system.
Fig. 5MSG parameter estimation error δ: a) ε=1, 0.9, 0.79, b) ε=0.78
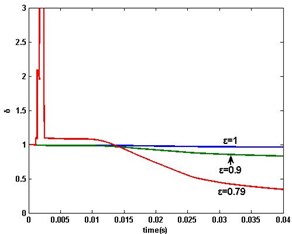
a)
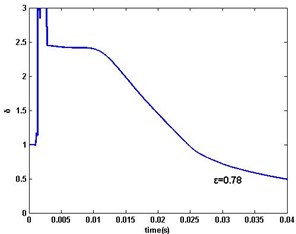
b)
Fig. 6MSG parameter estimation error δ when ω>0: a) ε=1, 0.9, 0.74, b) ε=0.73
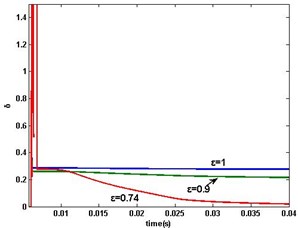
a)
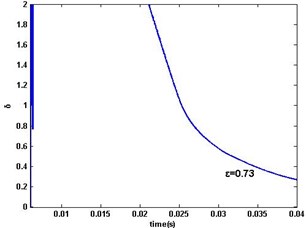
b)
According simulation results in Fig. 4-5, MSG algorithm for PMSM converges slow and the parameters estimation is inaccurate in finite time. In PMSM start-up period, especially when motor speed , it would result in poor parameter estimates that PMSM is reversible under the load. In order to eliminate the influence of the load, MSG algorithm is not used to estimate parameters until motor speed in the motor start-up period. The estimation errors with , , and are illustrated in Fig. 6. Comparing to Fig. 5, it can be observed that the proposed algorithm estimates the parameters with better accuracy, and also with an optimal value.
4.2. Parameters identification for dual-rate system
In the test, the PMSM system inputs () will be updated with period and the outputs () sampled with period .
Here, we can calculate the parameter vector of PMSM dual-rate model Eq. (11) as:
From the true value of the parameter of PMSM dual-rate model, it is well-known that the span of the components of the parameter vector is much large, and that will bring premature convergence on DR-MSG algorithm. To avoid the premature convergence, we can get the key components from the parameter vector . The new parameter vector and the corresponding input-output vector can be expressed respectively as:
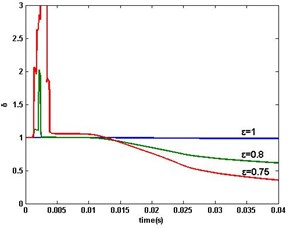
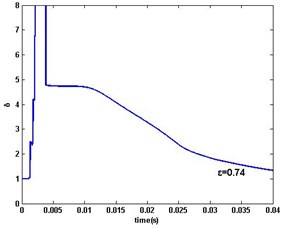
Fig. 7DR-MSG parameter estimation error δ: a) ε=1, 0.8, 0.75, b) ε=0.74
a)
b)
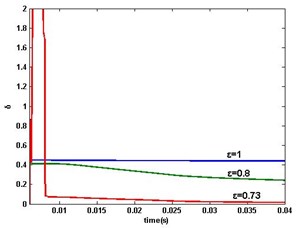
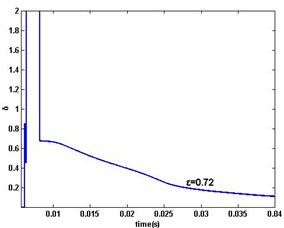
Fig. 8DR-MSG parameter estimation error δ when ω>0: a) ε=1, 0.8, 0.73, b) ε=0.72
a)
b)
Fig. 9Comparison between the proposed DR-MSG and MSG
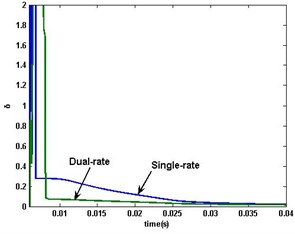
The PMSM parameter estimation errors of DR-MSG algorithm are shown in Fig. 7 (whole procedure) and Fig. 8 (). The aforementioned results in the single-rate simulation are also obtained. Comparison with MSG in PMSM’s single-rate data-sampled system is shown in Fig. 9. The two estimations are with optimal values respectively. From the comparison, it is observed that DR-MSG is with the higher convergence performance, and what’s more, DR-MSG algorithm estimates the motor parameters on the missing outputs.
5. Experimental results
The experimental results have been obtained with a 0.375-kW PMSM with a control board base on TMS320F2812 DSP. The configuration of PMSM drive plant is shown in Fig. 10. The experimental equipment includes magnetic powder brake for applying load torque to the motor, an optical encoder for position feedback. The data are sampled with the period 1 ms, and then been loaded into ‘MATLAB’ to analyze the results. The velocity of reference input is 300 r/min, and the load can be adjusted by the magnetic powder brake DC current. To clearly analyze the convergence performance of DR-MSG, the estimation errors are illustrated in Fig. 11 with the brake current 20 mA. It is clearly proved that for smaller , the convergence performance is becoming better. The same results can be obtained as the simulation.
Fig. 10Experiment plant of PMSM driver

Fig. 11DR-MSG parameter estimation error δ
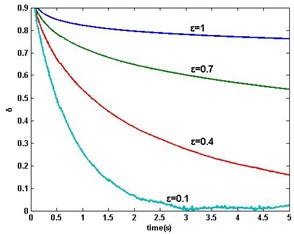
Fig. 12Comparison between DR-MSG and DR-RLS [11]
![Comparison between DR-MSG and DR-RLS [11]](https://static-01.extrica.com/articles/15142/15142-img16.jpg)
Fig. 13Comparison between brake current 20 mA and 160 mA
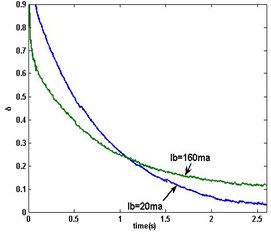
The dual-rate recursive least squares algorithm (the DR-RLS for short) [11] is applied to the PMSM’s dual-rate sampled-data system. Comparing with DR-MSG, the estimation results are shown in Fig. 12. From the comparison, it is observed that the convergence accuracy of DR-MSG algorithm is very close to that of the DR-RLS algorithm [11], and what is more, it has lower computation load than the DR-RLS algorithm. Furthermore, the magnetic powder brake DC current is adjusted to 160 mA in order to increase the load. Comparing with the aforementioned experiment, the DR-MSG ( 0.1) estimation errors are shown in Fig. 13. From the experiment results, it is proved that the load disturbs the parameter estimation of DR-MSG algorithm.
6. Conclusions
In this paper, the dual-rate model of PMSM is deduced with polynomial transformation technique. A novel modified stochastic gradient algorithm is presented for the parameter estimation of the PMSM’s dual-rate sampled-data system. Simulation and experimental results demonstrate the effectiveness of the proposed DR-MSG algorithm. The estimated parameters are closer to the actual ones for smaller convergence index . Both simulation and experimental results show that the applied load has a direct impact on the parameter estimation.
References
-
Bolognani S., Zigliotto M., Unterkofler K. On-line parameter commissioning in sensorless PMSM drives. Proceedings of the IEEE International Symposium on Industrial Electronics, Vol. 2, 1997, p. 480-484.
-
Ichikawa S., Tomita M., Doki S., et al. Sensorless control of permanent-magnet synchronous motors using online parameter identification based on system identification theory. IEEE Transactions on Industrial Electronics, Vol. 53, Issue 2, 2006, p. 363-372.
-
Underwood S. J., Iqbal H. Online parameter estimation and adaptive control of Permanent-Magnet synchronous machines. IEEE Transactions on Industrial Electronics, Vol. 57, Issue 7, 2010, p. 2435-2443.
-
Shehata E. G. Speed sensorless torque control of an IPMSM drive with online stator resistance estimation using reduced order EKF. International Journal of Electrical Power and Energy Systems, Vol. 47, Issue 1, 2013, p. 378-385.
-
Zhu Z., Zhu X., Sun P. Estimation of winding resistance andPM flux-linkage in brushless AC machines by reduced-order extended Kalman filter. International Conference on Networking, Sensing and Control, 2007, p. 740-745.
-
Liu K., Zhang Q., Chen J., et al. Online multiparameter estimation of Nonsalient-Pole PM synchronous machines with temperature variation tracking. IEEE Transactions on Industrial Electronics, Vol. 58, Issue 1, 2011, p. 1776-1788.
-
Jabbar M. A., Dong J., Liu Z. Determination of machine parameters for internal permanent magnet synchronous motors. Second International Conference on Power Electronics, Machines and Drives, 2004, p. 805-810.
-
Bechouche A., Sediki H., Abdeslam D. O., et al. Identification of induction motor at standstill using artificialneural network. The 36th Annual Conference of the IEEE Industrial Electronics Society, 2010, p. 2908-2913.
-
Mobarakeh B. N., Meibody-Tabar F., Sargos F. M. Mechanical sensorless control of PMSM with online estimation of stator resistance. IEEE Transactions on Industry Applications, Vol. 40, Issue 2, 2004, p. 457-471.
-
Rashed M., Macconnell P. A., Stronach A. F., et al. Sensorless in direct-rotor-field-orientation speed control of a permanent-magnet synchronous motor with stator-resistance estimation. IEEE Transactions on Industry Applications, Vol. 54, Issue 3, 2007, p. 1664-1675.
-
Ding J., Ding F. The residual based extended least squares identification method for dual-rate systems. Computers and Mathematics with Application, Vol. 56, Issue 6, 2008, p. 1479-1487.
-
Sheng J., Chen T., Shah S. L. Optimal filtering for multirate systems. IEEE Transactions on Circuits and Systems – II: Express, Vol. 52, Issue 4, 2005, p. 228-232.
-
Han Li-Li, Ding F. Identification for multirate multi-input systems using the multi-innovation identification theory. Computers and Mathematics with Applications, Vol. 57, Issue 9, 2009, p. 1438-1449.
-
Xiao J. Multirate Digital Control Systems. Beijing, Science Press, 2003, (in Chinese).
-
Rahmani H. A., Franklin G. F. Multirate control a new approach. Automatica, Vol. 28, Issue 1, 1992, p. 35-44.
-
Sahebsara M., Chen T., Shah S. L. Frequency-domain parameter estimation of general multi-rate systems. Computers and Chemical Engineering, Vol. 30, Issue 5, 2006, p. 838-849.
-
Li D., Shah S. L., Chen T. Identification of fast-rate models from multirate data. International Journal of Control, Vol. 74, Issue 7, 2001, p. 680-689.
-
Ding F., Liu P. X., Shi Y. Convergence analysis of estimation algorithms for dual-rate stochastic systems. Applied Mathematics and Computation, Vol. 176, Issue 1, 2006, p. 245-261.
-
Ding F., Liu P. X., Yang H. Parameter identification and intersample output estimation for dual-rate systems. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, Vol. 38, Issue 4, 2008, p. 966-975.
-
Ding J., Shi Y., Wang H., et al. A modified stochastic gradient based parameter estimation algorithm for dual-rate sampled-data systems. Digital Signal Processing, Vol. 20, Issue 4, 2010, p. 1238-1247.
-
Ding F., Chen T. Parameter estimation of Dual-Rate stochastic systems by using an output error method. IEEE Transactions on Automatic Control, Vol. 50, Issue 9, 2005, p. 1436-1441.
-
Berg M. C., Amit N., Powell J. D. Multirate digital control system design. IEEE Transactions on Automatic Control, Vol. 33, Issue 12, 1988, p. 1139-1150.
-
Hara T., Tomizuka M. Performance enhancement of Multi-rate controller for hard disk drives. IEEE Transactions on Magnetics, Vol. 35, Issue 2, 1999, p. 898-903.
-
Fujimoto H., Hori Y. Visual servoing based on intersample disturbance rejection by multirate sampling control-time delay compensation and experimental verification. Proceedings of the 40th IEEE Conference on Decision and Control, 2001, p. 334-339.
-
Fujimoto H., Hori Y., Kawamura A. Perfect tracking control based on multirate feedforward control with generalized sampling periods. IEEE Transactions on Industrial Electronics, Vol. 48, Issue 3, 2001, p. 636-644.
-
Pongam S., Sangwongwanich S. Stability and dynamic performance improvement of adaptive full-order observers for sensorless PMSM drive. IEEE Transactions on Power Electronics, Vol. 27, Issue 2, 2012, p. 588-600.
-
Goodwin G. C., Sin K. S. Adaptive Filtering Prediction and Control. PrenticeHall, Englewood Cliffs, NJ, 1984.
About this article
This work was supported by the National Natural Science Foundation of China (Grant No. 51177137).
