Abstract
With fuel consumption, the fuel container system vibrates with decreasing mass, which is a typical variable mass system. This paper investigates the dynamic characteristics of flexible rectangular fluid containers with decreasing liquid. The dynamic equations of the container with time varying liquid are derived by combining finite element method (FEM) and virtual mass method (VMM). Free vibration states of the variable mass system are mainly investigated. The vibration signals are decomposed using Choi-Walliam Distribution, and the energy density spectrum is given by time frequency analysis. Results show that decrease of the liquid of the system induces increase of the vibration frequencies of the system, and generates an additional negative damping causing the vibration decay slowly. It is found that the additional damping is proportional to rate of mass change. The additional negative damping can cause the system vibrate with increasing amplitudes while the negative damping plays the dominant role rather than the structural damping.
1. Introduction
The liquid storage containers are widely used to store vital products, such as petroleum products for transport facilities and aerospace industries (wing containers of aircraft, liquid propelled launchers, etc.). The dynamic behaviors of the fluid-structure coupled systems are important for design and safe use of the liquid storage container. In the previous study of vibration of containers containing liquid [1], the container wall and foundation were assumed to be rigid. The impulsive pressure resulting from the liquid mass accelerating due to the ground acceleration was taken into consideration in the study. Moiseev [2] constructed normal mode functions by integral equations in terms of Green’s function of the second kind. Chu [3] generalized Moiseev’s method by employing a perturbation technique using the characteristic functions to determine the subharmonic response of an arbitrary tank to an oscillatory axial excitation. In aerospace industries, NASA investigated the dynamic behavior of liquids in moving containers in 1966 [4].
For simplicity, the effect of liquid on the structure dynamics was considered as a set of simple resonators (mass-spring or pendulum) [5-7]. It is simple to estimate the low natural frequencies of the coupling system by this method. Hence in the aerospace domain, this approach is still widely used. The influence of motion of propellant on the control properties of launch vehicles were investigated utilizing this simplified model [8-11]. For more accurate results, many approximation methods were developed. J. D. Wang et al. [12-13] studied sloshing response of liquid in a rigid cylindrical container with multiple annual rigid baffles subjected to lateral excitations by a semi-analytical approach based on the mode superposition method. In E. Askari’ study [14], the interaction between the fluid and the structure was taken into account applying the Rayleigh quotient and Galerkin method. S. Rebouillat and D. Liksonov [15] introduced recent studies devoted to the problem of modeling the solid-fluid interaction in partially filled liquid containers. M. Eswarana et al. [16] investigated the difference between baffled and un-baffled containers, and numerical simulation and experimental validation were both given. J. R. Shao et al. [17] developed an improved analytical method to model the liquid structure coupling system. R. Belakroum et al. [18] presented a numerical partitioned strongly coupled approach to the vibration in containers partially filled with liquid, the obtained numerical results agreed with analytical results. O. Andrianarison and R. Ohayon [19] derived the basic equations describing the interactions between acoustic and gravity waves and constructed appropriate variational formulations. For fluid rectangular containers, the Rayleigh-Ritz method was useful for modelling the fluid-structural coupling system [20, 21].
Many numerical methods were used in analyzing the dynamic behavior of in liquid-filled containers. M. Sauer [22] utilized the adaptive SPH approach to solve impact problems on fluid-filled containers with complete rupture of the container, obtaining a good result. Xiang Xu et al. [23] developed a novel matrix method for a liquid-filled circular cylindrical shell with partially constrained layer damping. The finite element method was utilized to study the dynamic interaction between the liquid and elastic container-baffle system [24-26]. P. Pal et al. [27] dealt with the numerical and experimental studies of motion of liquid in partially filled prismatic containers subjected to external excitation by meshless local Petrov-Galerkin (MLPG) method.
Actually, the flexible fluid containers with time varying fluid are complicated systems. On the one hand, they are classical fluid-structure coupling system; on the other hand they are time varying systems. During transportation of fluid containers, impacts take place inevitably because of various causes. Recently, baffles are widely used to suppress the fluid sloshing in fluid containers transported by trucks. However, the time varying liquid affects the dynamic characteristics of the systems significantly. Especially for rockets, the ratio between the propellant mass and the initial mass of the vehicle can reach 95 %. Liquid propelled launchers or containers with fluid transported are greatly influenced by the inertial forces of internal fluid. These forces are proportional to the acceleration of wetted surface, and can consequently be represented by fictive fluid mass that vibrates along with the walls of the containers. This fictive mass is called “hydrodynamic added mass” [28-30], which in addition to the structure mass represents “virtual mass” [31-34]. In dynamic analysis of liquid propelled launchers or containers with fluid transported, virtual mass method has been widely used to model the liquid-structure coupling system for its simplicity and practicability [32-34]. Hence for liquid propelled launchers or containers with fluid transported by a truck, the sloshing of the fluid and the free surface influence the dynamic characteristics of the system little, while the most important role of the liquid is the additional mass of the system.
In previous studies, the dynamic behaviors of containers with constant liquid were usually analyzed, however the liquid in the containers are usually consumables. The main purpose of this study is to organize an efficient numerical procedure to analyze the effect of time varying liquid on the response of fluid storage containers, considering the coupling of the elastic container and time varying liquid. To take into account the fluid-structure interaction phenomenon, the liquid region is modeled by virtual mass method. The coupled equations for the fluid-structure modes are derived based on FEM and VMM. The main effect of time varying mass is investigated based on time frequency analysis. Finally, some conclusions are briefly summarized.
2. Basic equations
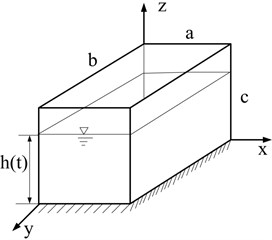
Consider a generic internal fluid-structure system shown in Fig. 1. The flexible container with the fluid in it is viewed as a coupled hydroelastic system. A rectangular tank with four flexible vertical walls of uniform thickness and a horizontal rigid bottom is partially filled with incompressible and non-viscous liquid of depth , as shown in Fig. 1. is a function of time . The side lengths and height of the tank are , and , respectively. The walls of the tank are considered as thin plates made of linearly elastic, homogeneous and isotropic material and are assumed to perform transverse bending deflection but no in-plane deformation. The motion of the liquid is assumed to be frictionless and irrotational so that the velocity distribution of the liquid may be represented as a gradient of the velocity potential.
Fig. 1A rectangular container partially filled with liquid
If is the pressure within the fluid and is the vector of fluid displacements, then its dynamic behavior is governed by the Euler’s equation:
The boundary conditions must be satisfied:
a) At liquid-structure interface:
b) At liquid free surface:
However, if free surface wave of the liquid is ignored, we have .
c) At the bottom of the container:
where – the vector of wetted structural displacements, – density of fluid, – the value of the acceleration acting normal to the free surface, – outward unit normal to the fluid surface.
The fluid displacement can be expressed in terms of a potential function as follows:
Because the fluid is incompressible and irrotational, the following functions are derived:
Substituting Eq. (5) into Eq. (1) and integrating gives the following differential equation for the fluid:
The following is a brief overview of the virtual mass approach in MSC. Nastran [34]. The Helmholtz method used by MSC. Nastran solves Laplaces equation by distributing a set of sources over the outer boundary, each producing a simple solution to the differential equation. By matching the assumed known boundary motions to the effective motion caused by the sources, we can solve a linear matrix equation for the magnitude of the sources. The values of the sources determine the effective pressures and, thereby, the forces on the grid points. Combining all of these steps into a matrix equation results in a virtual mass matrix as derived below. If is the value of a point source of fluid (units are volume flow rate per area) located at location , and is assumed acting over an area , the potential at any other point is:
where is the unit vector in the direction from point to point . Note that the gradient of the vector is the potential function which satisfies Laplace’s equation on a term by term basis. The other set of necessary equations are the pressures at any point in terms of the density , sources and geometry, namely:
The results of integrating Eq. (9) and Eq. (10) over the finite element surfaces are collected respectively in two matrices and , where:
where are the forces at the grid points. The matrix is obtained by integrating Eq. (11).
An additional area integration is necessary to convert the pressures to forces. A mass matrix may now be defined using Eq. (11) and Eq. (12) as:
where the virtual fluid mass matrix is:
For a container filling with constant liquid, the potential energy and kinetic energy can be written as:
where and are the mass matrix and stiff matrix of the elastic structure. For a fluid-structure coupling system with variable mass in a container of spacecraft, the mass of the system decreases in flight. The effect of the fuel on the stiffness of the structure can be neglected. Hence the potential energy for the time varying mass system is defined as:
The dynamic equations of the variable mass system can be derived according to Lagrange equation:
Substituting Eqs. (16)-(17) into Eq. (18), the dynamic matrix equations can be written as:
where is the external force vector, and is derivative of additional mass. From Eq. (19), an additional damping is induced by the change of the mass. If the mass increases, an additional positive damping is induced, while the mass decreases, an additional negative damping is induced. It should be noted that the additional negative damping may cause instability of the vibration. Let is the Rayleigh damping matrix, which is the form of:
Rayleigh damping coefficients can be determined by the first two natural frequencies:
where and are frequencies, and are damping ratios.
The final dynamic matrix equations can be expressed as Case I:
For the sake of contrast, a special Case II is also considered:
For this case, the additional damping is not taken into account. Therefore, the effect of the additional damping on the dynamic characteristics of the container can be verified.
3. Numerical procedure
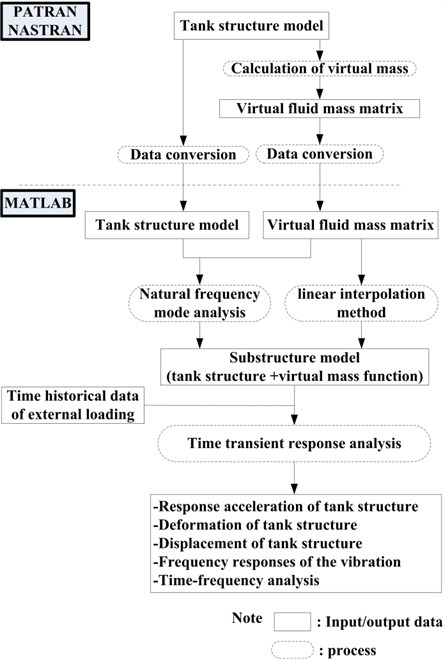
A calculation procedure based on MATLAB is used for modal analysis, dynamic analysis and signal processing, in conjunction with PATRAN-NASTRAN, which is widely used for linear structural and vibration analysis of aircrafts. Fig. 2 shows a procedure for dynamic analysis and signal processing of a container with time varying mass. The virtual fluid mass can be directly calculated based on the PATRAN-NASTRAN virtual mass calculation program. However, as PATRAN-NASTRAN is basically a linear analysis code for time invariant system, useless results are often obtained for time varying models. MATLAB is more suitable for nonlinear calculation, but complicated fluid modeling and large-scale calculation are necessary to calculate the impulsive mass using fluid-structure interaction analysis for this container with time varying mass. Based on this consideration, only virtual mass are to be calculated by PATRAN-NASTRAN. The obtained virtual mass data are converted into a MATLAB code to carry out the dynamic analysis. The response acceleration and displacement are calculated using Newmark direct integration method. After that, time frequency analysis is developed to study the characteristic of the time varying mass system. The vibration signals are decomposed by Choi-Walliam distribution, therefore time frequency features of the time varying mass system are obtained.
Fig. 2The flow chart of the calculation
4. Comparison study
In this section, a comparison study is first given to determine the validity of the theoretical formulation in computing dynamic responses of the flexible storage tank. The dimensionless natural frequencies () of wall vibration are expressed as:
where , and are the flexural rigidity, the wall thickness and density of the tank wall, respectively. is the circular natural frequency of the container and:
where and are the Young’s modulus and Poisson’s ratio of the tank wall. The first six dimensionless natural frequencies of wall vibration (impulsive modes) of the empty cubic tank () and a cubic tank fully filled with liquid which has a mass ratio of the liquid to the tank-wall equal to 5 are presented in Table 1 and compared with those presented by Zhou and Liu [20] and S. Hashemi [21]. A mesh grid of 20×20 is used for each wall surface. Good agreements are observed for all cases, as shown in Table 1. The parameter effects on eigen frequencies of the liquid-tank system are investigated for a cubic tank. The effect of the liquid depth on the first six bulging eigen frequencies is given in Table 2 when the tank is partially filled with the liquid. One can see that the bulging eigen frequencies decrease with the increase of the liquid depth.
Fig. 3Finite element model of a filled cubic tank
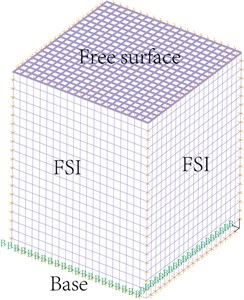
Table 1Comparison on the first six impulsive frequencies of the empty and filled cubic tank
Frequency | Empty cubic tank | Cubic tank filled with liquid | ||||
Present study | S. Hashemi [21] | Zhou [20] | Present study | S. Hashemi [21] | Zhou [20] | |
17.509 | 17.619 | 17.632 | 8.318 | 8.212 | 8.48 | |
35.910 | 36.049 | 36.045 | 18.615 | 18.011 | 18.175 | |
51.775 | 52.076 | 52.133 | 26.112 | 26.742 | 26.212 | |
70.988 | 71.389 | 71.208 | 39.451 | 38.484 | 37.494 | |
74.040 | 74.377 | 74.576 | 42.721 | 42.441 | 42.931 | |
106.203 | 106.297 | 107.531 | 59.025 | 60.470 | 58.016 | |
Table 2The effect of the ratio of liquid-depth to tank-height on the first two bulging eigenfrequencies
Present study | Zhou [21] | Present study | Zhou [21] | |
0.5 | 15.845 | 15.956 | 25.920 | 24.974 |
0.6 | 14.056 | 14.146 | 24.593 | 23.544 |
0.7 | 12.267 | 12.358 | 24.339 | 22.998 |
0.8 | 10.691 | 10.865 | 23.461 | 22.134 |
0.9 | 9.467 | 9.636 | 21.627 | 20.489 |
The convergence study on the fundamental impulsive frequencies with respect to the term number of the mesh grids is shown in Table 3. It is seen that the impulsive frequencies monotonically decrease with the increase of the number of the mesh grids. The results show rapid convergence to the present method. The present method is now applied to investigate dynamic response characteristics of 3-D rectangular fluid storage tanks.
Table 3The convergence study on the fundamental frequencies with respect to number of mesh grids
Fundamental dimensionless natural frequency | Mesh grids of the tank wall | |||
5×5 | 10×10 | 15×15 | 20×20 | |
Empty cubic tank | 18.735 | 17.742 | 17.569 | 17.50 |
Cubic tank filled with liquid | 9.196 | 8.495 | 8.366 | 8.318 |
5. Numerical example
Since rectangular tanks are used most often for the wet-type storage of spent fuel assemblies, a typical dimension for those tanks is selected for the next example [24]. The material properties are: the density ; the Young’s modulus ; and the Poisson’s ratio . The model is designed according to the following geometric specifications: the height the wall thickness the length and the width, . The tank is assumed to be fixed to the ground ideally, and to have 1 % structural damping. The effect of the liquid in the tank on the stiffness of the structure is small, however the liquid influences the total mass of the structure much. Hence, the vibration frequency will get bigger as the liuqid decreases. The finite element model and the bulging mode shapes of the first three order of the rectangular container shown in Fig. 4 and Fig. 5. From the mode shapes, deformation at Node 389 in direction is large, hence the responses of Node 389 in direction is monitored. Table 4 gives the natural frequencies of the containers with different ratio of liquid-depth to tank-height. The natural frequency of the system is related directly to the liquid-depth. As introduced above, the value of the frequency get lowered remarkably resulting from a large ratio of liquid-depth to tank-height. From Table 4, the frequency of the first order bulging vibration increases from 6.696 Hz to 16.933 Hz, as the ratio of liquid-depth to tank-height decreases from 1 to 0.1.
Fig. 4Finite element model and mode 1st of the tank
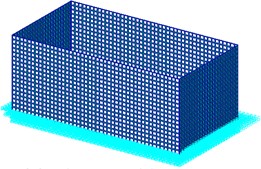
a) Finite element model
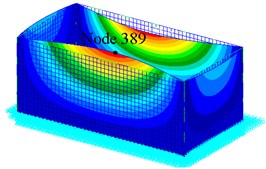
b) Mode 1
Fig. 5Mode shapes of the tank
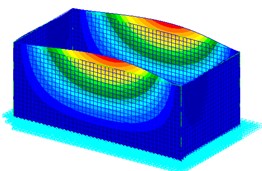
a) Mode 2
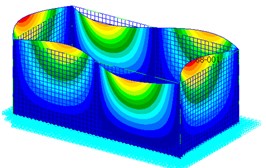
b) Mode 3
Table 4The first three coupling eigenfrequencies for different ratio of liquid-depth to tank-height
0.1 | 16.933 | 17.750 | 29.442 |
0.2 | 16.922 | 17.139 | 29.416 |
0.3 | 16.845 | 17.658 | 29.247 |
0.4 | 16.545 | 17.345 | 28.631 |
0.5 | 15.754 | 16.524 | 27.125 |
0.6 | 14.282 | 15.018 | 24.604 |
0.7 | 12.319 | 13.042 | 21.588 |
0.8 | 10.288 | 11.011 | 18.657 |
0.9 | 8.470 | 9.186 | 16.039 |
1 | 6.696 | 7.642 | 13.738 |
The vibration responses of the container in direction with decreasing liquid are calculated using Newmark direct integration method. In Fig. 6(a) and Fig. 6(b), the displacement responses and frequency responses of the container with decreasing liquid are illustrated, and the responses for Case I and Case II are compared. In Fig. 6(a), from the two curves, it is found for Case I, a negative damping is induced resulting from the decreasing mass. The negative damping influences the vibration significantly, and the amplitude of the vibration increases. For Case II, the structural damping causes the vibration decay. The displacement signals are processed by Fourier transformation, as shown in the right one. From the frequency response curves, it is observed that the vibration frequency of the system consists of a series of frequencies. The frequency ranges from about 7 Hz to 17 Hz, coincided with the frequency listed in Table 4. The range of the frequency can be determined by the range of the mass of the system. From the results shown in Fig. 6 and Fig. 7, the influence of the negative damping is remarkable so that the additional damping cannot be neglected in the analysis of containers with time varying mass.
Fig. 6Response curves of Node 389 in y direction
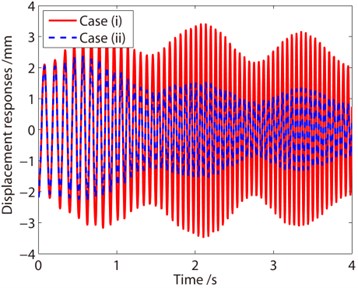
a) Displacement response curves
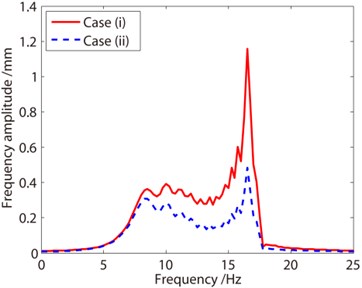
b) Frequency response curves
6. The effect of the rate of mass change
As depicted in Eq. (19), the induced damping is proportional to the rate of mass change. In other words, if the mass of the system decreases fast, a large negative damping is generated. In this section, the liquid decreases in 1 s, meaning that the rate of mass change increases by 4 times, hence a large negative damping is induced. From the displacement curves in Fig. 7, one can find that for Case I the negative damping induces increase of the vibration amplitude, and for Case II, the structural damping influences the vibration much, which causes decay of the vibration. From the frequency response curves, the vibration frequency increases from about 7 Hz to 17 Hz. Compared with curves shown in Fig. 6, the amplitude of the vibration increases more resulting from the additional negative damping. In Fig. 6(b), the maximum amplitude is 1.2 mm, while in Fig. 7(b) the maximum amplitude is 1.8 mm. In other words, the influence of the negative damping must be taken into account in the analysis of container with decreasing mass.
Fig. 7Response curves of Node 389 in y direction
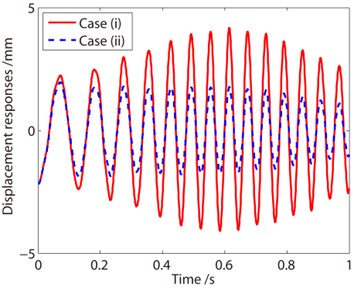
a) Displacement response curves
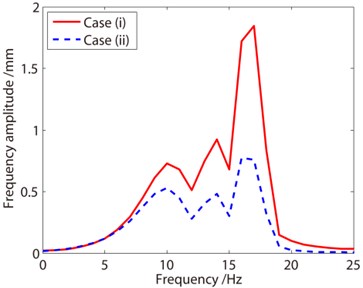
b) Frequency response curves
7. Time frequency analysis
With change of mass of the system, the frequency of the system is changing as well. The classical Fourier Transformation cannot give enough information of the vibration signals in time-frequency domain [35]. In this section, the time frequency analysis is used to analyze the time-domain signals. It has been shown that the class of time-frequency energy distributions have the following general expression [36]:
where is the time signal, is its complex conjugate and is a two-dimensional function called the parameterisation or kernel function, representative of the particular distribution. This class of distributions, known as the Cohen’s class, uses a bilinear transformation that depends on two variables: time and frequency. Depending on the specific kernel function used for the bilinear transformation, various different distributions have been proposed.
Choi and Williams succeeded in devising a distribution for which the spurious values are minimal. It diminishes the effects of the cross-terms within the range while retaining the desirable properties [35]. There are many papers demonstrating effectiveness of CWD [36-38]. The Choi-Williams distribution (CWD) is a member of Cohen’s class with kernel:
where is a constant scaling factor to suppress the cross-terms. By substituting this kernel into Eq. (26), the CWD is obtained:
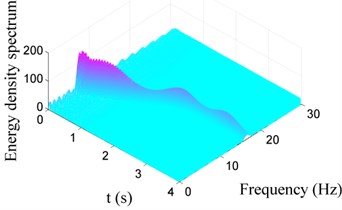
Fig. 8 shows the Choi-Williams distribution of vibration signals displayed in Fig. 6(a). As the mass of the system decreases, the vibration frequency increases. The change of the vibration frequency versus time is also given by Choi-Williams distribution, which cannot be found employing classical Fast Fourier Transformation. In Fig. 8(a), the power spectral density of the vibration response for Case I is displayed. It is observed that the decrease of the mass induces a negative damping, causing increase of the energy of the system. Comparing the contour in Fig. 8(a) and Fig. 8(b), we can find that the energy density in Fig. 8(a) is larger than that in Fig. 8(b). The reason is that the negative damping induced by the decreasing mass has a great influence on vibration of the container. The results show that CWD is an efficient tool to decompose non-stationary signal.
The change of the vibration frequency versus time can also be obtained bases on Choi-Williams distribution, as shown in Fig. 9. It can be found that the vibration frequency increases from 7 Hz to 17 Hz, coincided with that listed in Table 4. Using classical Fast Fourier Transformation, the range of the vibration frequency can be obtained, but the change of the vibration frequency versus time cannot be given.
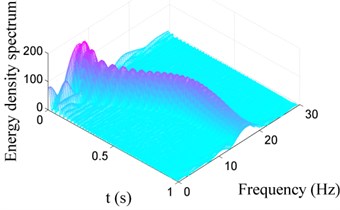
Similarly, Fig. 10 and Fig. 11 show the Choi-Williams distribution of vibration signals displayed in Fig. 7. In Fig. 10, one can also find that the additional negative damping induces increase of the energy density, hence the energy density for Case I is much larger than that for Case II as shown in Fig. 10(b). The change of the vibration frequency versus time can also be obtained bases on Choi-Williams distribution, as shown in Fig. 11. It can also be found that the vibration frequency increases from 7 Hz to 17 Hz in 0 s-1 s, coincided with that listed in Table 4.
Fig. 8Choi-Williams distribution of vibration signals for Case I with different damping
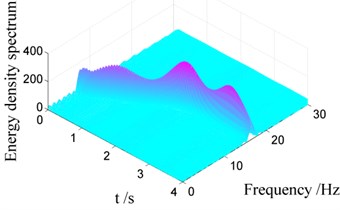
a) Case I
b) Case II
Fig. 9Choi-Williams distribution of vibration signals for Case i with different damping
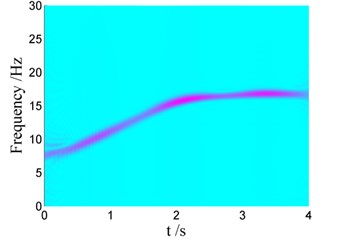
a) Case I
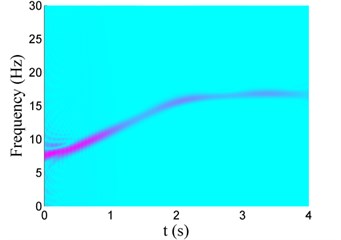
b) Case II
Fig. 10Choi-Williams distribution of vibration signals for Case I with different damping
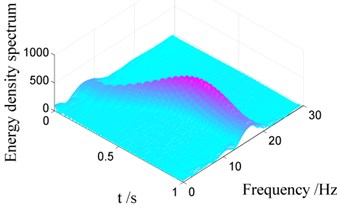
a) Case I
b) Case II
Fig. 11Choi-Williams distribution of vibration signals for Case i with different damping
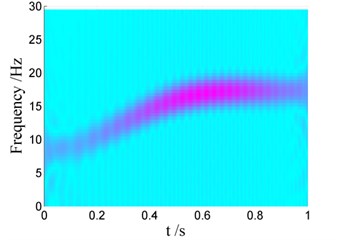
a) Case I
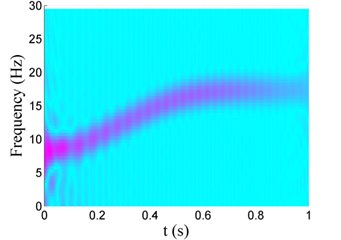
b) Case II
8. Conclusions
In this paper, free vibration states of an elastic rectangular container with time varying mass were discussed. The decease of the internal liquid (like fuels) was taken into account in the numerical study of container structures. The fluid-structure coupling was analyzed as a time varying mass system. A numerical procedure was constructed to solve vibration problems of this time varying mass system, using MATLAB in conjunction with PATRAN-NASTRAN. Conclusively, in this study, the influence of the fluid sloshing is neglected, and the effect of the deceasing fluid on flexible containers is mainly investigated. From the engineering point of view, the following conclusions have been drawn:
1) The vibration frequencies increases with the decrease of the mass, and the range of the frequency can be determined by the range of the mass. From the dynamic equations, a negative damping is induced as the mass of the system decreases. The negative damping is an unstable parameter. In the vibration, the negative damping can slow down the decay amplitude. If the effect of the negative damping exceeds the effect of the structural damping, the amplitude of the vibration increases. In the simulation of vibration of containers with time varying mass, the negative damping cannot be neglected. The negative damping is proportional to rate of mass change. If the mass of the system changes fast, a big negative damping is induced, and the big negative damping can cause instability of vibration of the system.
2) For the time varying mass system, the time frequency feature is obtained using Choi-Williams distribution. The energy density spectrum and the change of the frequency versus time are displayed. Choi-Williams distribution is a useful tool to analyze non-stationary signals of time varying mass system.
3) In the study, the influence of slosh of the liquid the vibration of the system is little comparing with the influence of the time varying mass. The proposed method can be used to solve similar problems in engineering.
4) Further work intends to study dynamic behavior of containers with fuel consumption under different load cases. More work is still necessary in order to fully exploit the coupling between the fluid sloshing and time varying mass. As the decreasing mass induces an additional negative damping, stability analysis for time varying mass system is to be developed. In addition, an experiment will be provided for verification in detail.
References
-
Housner G. W. The dynamic behavior of water containers. Bulletin of the Seismological Society of America, Vol. 53, 1963, p. 381-387.
-
Moiseev N. N. Introduction to the theory of oscillations of liquid-containing bodies. Advances in Applied Mechanics, Vol. 8, 1964, p. 233-289.
-
Wen-Hwa Chu Subharmonic oscillations in an arbitrary tank resulting from axial excitation. Journal of Applied Mechanics, Vol. 35, 1968, p. 148-154.
-
Abramson H. N. The dynamic behaviour of liquids in moving containers. NASA SP-106, 1966.
-
Graham E. W., Rodriguez A. M. The characteristics of fuel motion which affect airplane dynamics. Journal of Applied Mechanics, Vol. 19, 1951, p. 381-388.
-
Abramson H. N., Chu W. H., Ransleben G. E. Representation of fuel sloshing in cylindrical containers by an equivalent mechanical model. ARS Journal, Vol. 31, 1961, p. 1697-1705.
-
Lomen D. O. Liquid propellant sloshing in mobile containers of arbitrary shape. Technical Report CR-222, NASA, 1965.
-
Ranganathan R., Ying Y., Miles J. B. Development of a mechanical analogy model to predict the dynamic behavior of liquids in partially filled container vehicles. Mechanical Engineering Congress and Exposition Washington, 2003.
-
Bao G. W., Liu Y. Spatial pendulum analogy of liquid sloshing on three-axis stabilized spacecraft. Selected Scientific Papers, Shanghai Jiao Tong University Press, 1994, p. 105-112.
-
Cho S., Clamroch N. H. M., Reyhanoglu M. Feedback control of a space vehicle with unactuated fuel slosh dynamics. Proceedings of the AIAA Guidance, Navigation, and Control Conference, 2000, p. 14-17.
-
Dai L., Xu L., Setiawan B. A new non-linear approach to analysing the dynamic behaviour of container vehicles subjected to liquid sloshing. Proceedings of the Institution of Mechanical Engineers, Part K, Journal of Multi-body Dynamics, Vol. 219, 2005, p. 75-86.
-
Wang J. D., Lo S. H., Zhou D. Liquid sloshing in rigid cylindrical container with multiple rigid annular baffles: Free vibration. Journal of Fluids and Structures, Vol. 34, 2012, p. 138-156.
-
Wang J. D., Lo S. H., Zhou D. Sloshing of liquid in rigid cylindrical container with multiple rigid annular baffles: Lateral excitations. Journal of Fluids and Structures, Vol. 42, 2013, p. 421-436.
-
Askari E., Daneshmand F., Amabili M. Coupled vibrations of a partially fluid-filled cylindrical container with an internal body including the effect of free surface waves. Journal of Fluids and Structures, Vol. 27, 2011, p. 1049-1067.
-
Rebouillat S., Liksonov D. Fluid-structure interaction in partially filled liquid containers, a comparative review of numerical approaches. Computers and Fluids, Vol. 39, 2012, p. 739-746.
-
Eswarana M., Saha U. K., Maity D. Effect of baffles on a partially filled cubic container, Numerical simulation and experimental validation. Computers and Structures, Vol. 87, 2009, p. 198-205.
-
Shao J. R., Li H. Q., Liu G. R., Liu M. B. An improved SPH method for modeling liquid sloshing dynamics. Computers and Structures, Vol. 100-101, 2012, p. 18-26.
-
Belakroum R., Kadja M., Mai T. H., Maalouf C. An efficient passive technique for reducing sloshing in rectangular containers partially filled with liquid. Mechanics Research Communications, Vol. 37, 2012, p. 341-346.
-
Andrianarison O., Ohayon R. Compressibility and gravity effects in internal fluid-structure vibrations: Basic equations and appropriate variational formulations. Computer Methods in Applied Mechanics and Engineering, Vol. 195, 2006, p. 1958-1972.
-
Zhou D., Liu W. Hydroelastic vibrations of flexible rectangular tanks partially filled with liquid. International Journal for Numerical Methods in Engineering, Vol. 71, 2007, p. 149-174.
-
Hashemi S., Saadatpour M. M., Kianoush M. R. Dynamic behavior of flexible rectangular fluid containers. Thin Walled Structures, Vol. 66, 2013, p. 23-38.
-
Sauer M. Simulation of high velocity impact in fluid-filled containers using finite elements with adaptive coupling to smoothed particle hydrodynamics. International Journal of Impact Engineering, Vol. 38, 2011, p. 511-520.
-
Xiang Yu, Yuan Liyun, Huang Yuying, Ni Qiao A novel matrix method for coupled vibration and damping effect analyses of liquid-filled circular cylindrical shells with partially constrained layer damping under harmonic excitation. Applied Mathematical Modelling, Vol. 35, 2011, p. 2209-2220.
-
Hyun Moo Koh, Jae Kwan Kim, Jang-Ho Park Fluid-structure interaction analysis of 3-D rectangular tanks by a variationally coupled BEM-FEM and comparison with test results. Earthquake Engineering and Structural dynamics, Vol. 27, 1988, p. 109-124.
-
Mitra S., Sinhamahapatra K. P. 2-D simulationof fluid-structure interaction using finite element method. Finite Elements in Analysis and Design, Vol. 45, 2008, p. 52-59.
-
Mitra S., Sinhamahapatra K. P. Slosh dynamics of liquid-filled containers with submerged components using pressure-based finite element method. Journal of Sound and Vibration, Vol. 304, 2007, p. 361-381.
-
Pal P., Bhattacharyya S. K. Sloshing in partially filled liquid containers – numerical and experimental study for 2-D problems. Journal of Sound and Vibration, Vol. 329, 2010, p. 4466-4485.
-
Zienkiewicz O. C., Taylor R. L. The Finite Element Method, Vol. 1-2. McGraw-Hill, 2000.
-
Belytschko T. Methods and programs for analysis of fluid-structure systems. Nuclear Engineering and Design, Vol. 42, 1977, p. 41-52.
-
Zienkiewicz O. C., Bettess P. Fluid-structure dynamic interaction and wave forces: An introduction to numerical treatment. International Journal for Numerical Methods in Engineering Special Issue, Fluid Structure Interaction, Vol. 13, 1978, p. 1-16.
-
Erik Paul Sorensen, Pedro V. Marcal A solid mechanics approach to the solution of fluid-solid vibration problems by finite elements. Brown University Technical Report N00014-0007/13, 1976.
-
Christensen E. R., Brunty J. Launch vehicle slosh and hydroelastic loads analysis using the boundary element method. 38th Structures, Structural Dynamics, and Materials Conference, 1997.
-
Christensen E. R., Brunty J. A procedure for quick calculation of launch vehicle hydroelastic loads. Dynamics Specialists Conference, 1996, p. 347-257.
-
MSC.Nastran Version 70 Advanced Dynamic Analysis User’s Guide, MSC.Software Corporation.
-
Tao Yu, Qingkai Han Time frequency features of rotor systems with slowly varying mass. Shock and Vibration, Vol. 18, 2011, p. 29-44.
-
Cohen L. Time-frequency analysis, a review. Proceedings of the IEEE, Vol. 77, 1989, p. 941-981.
-
Zhang B., Sato S. A time-frequency distribution of Cohen’s class with a compound kernel and its application to speech signal processing. IEEE Transactions on Acoustical, Speech, and Signal Processing, Vol. 42, 1994, p. 54-64.
-
Jones D. A resolution comparison of several time-frequency representations. IEEE Transactions on Signal Processing, Vol. 40, 1992, p. 413-420.
About this article
The authors of the paper gratefully acknowledge the financial support from National Natural Science Foundation (Grant No. 11302160 and Grant No. 11102147) of China.
