On an inline conveyor resonantly driven by piezoelectric actuators

1. Introduction

A feeder (conveyor) is a mechanical equipment that can continuously or intermittently transport objects according to the specified route. Since the feeder can convey or process bulk materials with an economical and efficient way, it is extensively used in various production processes, e.g., in electronic, food, medical, mechanical, chemical industries, etc. Currently, it is one of indispensable automatic machinery.

Fig. 1Inline vibrating conveyor

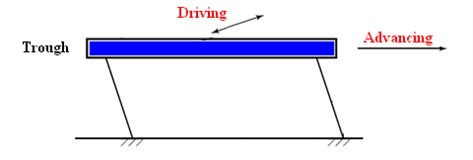
Fig. 2Vibratory bowl feeder [2]

Vibratory conveyors mainly comprise actuators to generate vibration, troughs (tubes) to transport objects or bulk materials, and springs (elastic members) to elastically support the troughs. Two widely-used vibratory feeders, classified by the moving path of the part or the shapes of the trough, are linear vibratory conveyors and vibratory bowl feeders, as shown Fig. 1 and Fig. 2, respectively. The objects move on the track of the trough due to the vibration produced by the actuator. A vibratory feeder has the disadvantages of large noise, huge volume, short feeding rate, and easy damage to the parts. In addition, its service life may be shortened owing to the fatigue caused by vibration. Therefore, many attempts have been made to enhance its performance.

In 1967 and 1972, Gaberson [1-3] established the theoretical model of inline vibrating feeders, and investigated the effect of conveyor parameters on the motion of conveying parts presents a theory that can predict the motion of particles on an oscillating conveyor. In 1969, Morcos and Massoud [4] proposed criteria for evaluating the efficiency of an inline conveyor. In 1971, Gladwell and Masour [5] presented the theoretical model for vibrating conveyors. In 1990, El-Shakery et al. [6] conducts the analysis and design of inline feeders driven by linkages. In 2005, Ting et al. [7] proposed an inline conveyor driven by a bimorph piezoelectric actuator, and its dynamic modeling, driving control circuit design, motion trajectory analysis, and optimal transport feed rate are examined. In 2009, Hsieh and Tsai [8] present a novel quick mechanism by employing a generalized Oldham coupling. In 2012, Hsieh and Tsai [9] proposed a novel inline vibrating feeder by using a generalized Oldham coupling, and conducted its approach of design and analysis. In 2013, Hsieh [10] presented a novel bowl vibratory feeder and its approach of kinematic analysis.

The purpose of this study is to propose a novel inline feeder vibrated with its resonant frequency, and verify its feasibility and effectiveness by kinematic simulations and experiments, respectively. In Section 2, the proposed new feeder will be presented. Then, Section 3 will be dedicated to address the methodology for optimal dimensional synthesis. Furthermore, Section 4 will present the procedure of modal analysis and resonant simulation. In Section 5, kinematic simulation will be carried out with a illustrate example. Section 6 will conduct the experiments. Finally, conclusions will be drawn in Section 7.

2. The proposed conveyor

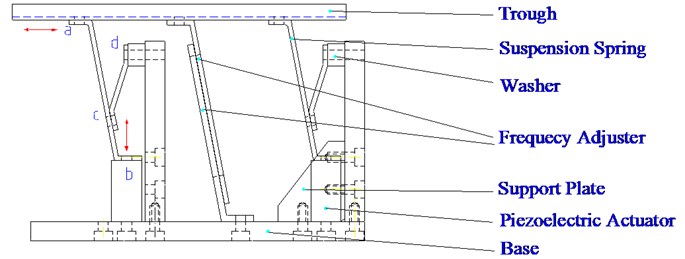
Fig. 3 shows the schematic of the proposed inline feeder, it mainly consists of a base, a piezoelectric actuator, a suspension spring, a natural frequency adjusting device, and a straight trough. The actuator drives the Scott-Russell (S-R) mechanism at one of the natural frequencies of the feeder, the trough will vibrate horizontally, and its motion will be significantly increased due to resonating and the amplification of the S-R mechanism. Moreover, the adjusting device will be implemented to adjust the frequency of the feeder. In addition, the first natural frequency of the feeder will be designed the same with the frequency of commercial electricity in Taiwan, the actuator is driven by directly using the electricity, no piezoelectric actuator driver is needed, hence, the building cost can be reduced.

Fig. 3Proposed inline conveyor

3. Optimum dimensional synthesis

An S-R mechanism transforms and amplify linear input motion to linear output motion perpendicular to the input, and is extensively used in micro-positioning platform [11], as shown in Fig. 4. It is a planar four-link mechanism, i.e., one frame, two links, and one slider. Also, it consists of three revolute joints and one sliding joints. If $ab=ac=ao$, then the path of point $c$ will be an exact straight line.

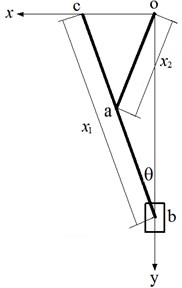
Optimization can be defined as the iterative methodology or process of finding the proper values of the parameters for a given problem by minimizing or maximizing the objective function subject to the given constraints. The purpose of the optimization for the proposed system is to maximize the displacement of point $c$, such that the system can advance the part in maximum. From Fig. 5, the position of $c$ can be obtained as:

where $x_1$ and $x_2$ are the design variables, and denote the link lengths of $bc$ and $oa$, respectively. For simplification, $ab$ is set as the same with oa in length. Hence, the displacement of $x_c$ can be found as:

The objective function and the design constraint can then be set as:

and

where $x_{il}$ and $x_{if}$ ($i=$1, 2) are the low bound and the upper limit of $x_i$, respectively. Therefore, the canonical form of the optimization is formulated. It can be found that it is a linear programming in which the constraints and the objective function are linear functions of design variables, and the simplex algorithm and the interior point method are two techniques commonly employed to solve this kind of problem. In addition, commercial software such as Matlab, Mathematica, ADAMS, etc., can also be used to solve the optimization problem.

Fig. 4Scott-Russell mechanism

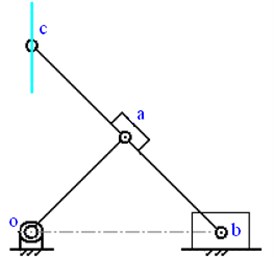
Fig. 5Kinematic dimensions of Scott-Russell mechanism

4. Modal analysis and resonant simulation

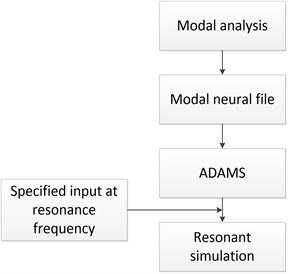
Resonant vibration is primarily caused by an interaction between the elastic and inertial properties of the materials within a structure. To excite the system to vibrate resonantly, the natural frequencies and the mode shapes of the design need to be firstly identified. Modal analysis is a widely used approach of finding the natural frequencies and the mode shapes of an elastic system. In this study, modal analysis, shown in Fig. 6, is conducted by using ANSYS software, its procedure is depicted in. The result of the modal analysis is introduced into ADAMS for resonant simulation, shown in Fig. 7, to verify the feasibility of the design. Their analytical procedures are summarized below:

1) Geometry. Geometry can be created in ANSYS or imported from other CAD software. It is generally more efficient to imported geometry.

2) Element typed. Element type should be specified according to the geometry. A shell element can be selected if the thickness, compared to its length and width, is negligible. Otherwise, a solid element should be chosen.

3) Material properties. To formulate a well-defined problem, Young’s modulus $E$, Poisson’s ratio $\upsilon$, and density $\rho$ of the materials have to be given according to the actual design. In addition, section properties are also need to be specified.

4) Mesh definition. To mesh a model precisely, meshing attribute, Element size (or Number of element divisions) for each material should be specified properly. Initially, a larger element size could be chosen, and an appropriate and smaller size at the final stage has to be specified till a convergence testing has been passed.

5) Boundary conditions. To obtain a correct mode of vibration, the degree of freedoms of each key point at the boundary should be constrained according the actual boundary conditions.

6) Modal analysis. Having specified applied the loading, the natural frequencies and the mode shapes can then be solved by ANSYS.

7) Post processing. Finally, the analytical results (displacement, stress, mode shape, etc.) can be textually/graphically presented and investigated by the Post Processing function of the software.

8) Resonant simulation. The analytical model is saved as the format of modal neutral file in ANSYS software, and then further introduced into ADAMS software for resonant simulation [12]. After the input has been specified at one of the natural frequencies, the resonant output motion of the design can then be simulated.

Fig. 6Modal analysis

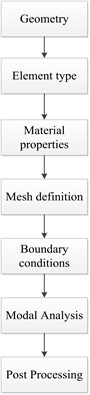
Fig. 7Resonant simulation

5. Design example

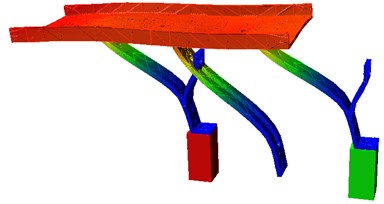
The optimization of the proposed design is conducted by using the design evaluation tool of ADAMS/View software, and it is found that $x_1=$43 mm and $x_2=$5 mm, respectively. To perform the modal analysis, the solid model of the trough and suspension springs of the proposed design is created. Element type is set as Solid/10node 92. Moreover, the material’s properties are specified in Table 1. The meshing of the model can then be conducted, as shown in Fig. 8. Furthermore, the boundary conditions shown in Fig. 9 are set according to the constraints at the boundaries with the base and the actuator. Finally, the natural frequencies are found as shown in Fig. 10. It is found that the 2nd and the 3rd natural frequencies are close to the expected frequency 60 Hz. Therefore, the design is feasible. In addition, the analytical model is introduced into ADAMS software for resonant simulation, as shown in Fig. 11. The input force are set to vibrate at the 3rd natural frequency, i.e., $f\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}(2\pi \bullet 62.473\bullet t)$. The simulated result depicts that the design can produce an amplified forward displacement.

Fig. 8Meshing

Fig. 9Boundary conditions

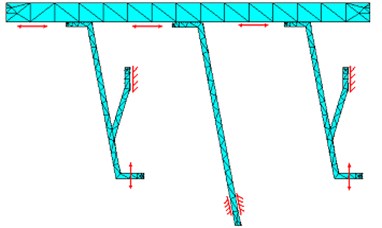
Fig. 10Natural frequencies

Fig. 11Resonant simulation

6. Experiments

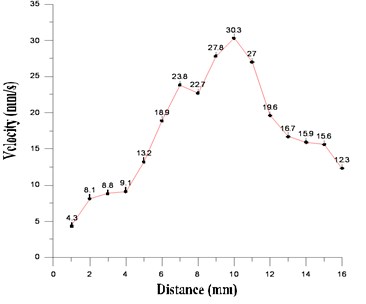
To verify the correctness of the simulation, the detailed design shown in Fig. 12 has been carried out, and the prototype shown in Fig. 13 is manufactured. A piezoelectric stack actuator (US EuroTEK, CTC-PSt 150/4/7 VS 9) is used as the driver, Table 2 shows its specification. There are two stroke options: 13 and 9 μm, the driving voltage of the latter should be 0-150 V. To save the building cost, the commercial electricity (±110 V, 60 Hz) in Taiwan is adopted as the input voltage of the propose system. Therefore a voltage transform is required. The input voltage is converted into ±75 V, then transformed, by a clamping circuit, into the required driving voltage (0-150 V). Since there is always a slight discrepancy between the analytic model and the prototype due to an imperfect modelling. The natural frequency of the prototype has to be finely tuned to close to the driving frequency. To this end, an adjusting device is designed, it alters the natural frequency by adjusting the span of the two bolts, as shown in Fig. 14. The experiments with different spans are conducted, and the results are shown in Fig. 15. It can be found from the figure that the advancing velocity reaches its peak at the span of 30 mm, hence the system vibrates resonantly at the driving frequency. Therefore its feasibility and correctness of the proposed design have been verified.

Fig. 12Assembly drawing with exploded view

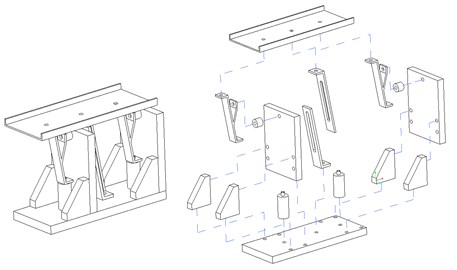
Fig. 13Prototype

Fig. 14Frequency adjusting advice

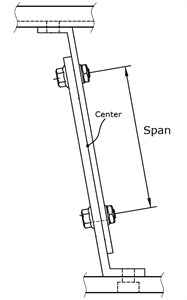
Fig. 15Frequency tuning

7. Conclusions

In this work, a new design for the inline conveyor has been proposed. The structure of the proposed design has been presented, and the approaches of optimal design and modal analysis have been presented. An illustrative example has been given, and kinematic simulation has been conducted by utilizing ADAMS software. The result has indicated that the proposed new design can effectively produce the winding motion of the shuttle. Therefore its feasibility has been verified.