Electromechanical fluidic coupled vibrations for micro film considering the van der Waals force

1. Introduction

Microelectromechanical Systems (MEMS) are the integrated systems consisting of microelectronics, microactuators and microsensors [1]. A typical MEMS consist of micro beams or micro films. An example is a small rectangular silicon film with sides in the order of $mm$ and thickness of the order of microns, that deforms when subject to electric fields. Owing to its small size, significant forces and deformations can be obtained with the application of low voltages. Examples of devices that utilize vibrations of such films are synthetic microjets, and microspeakers, etc [2]. Some devices are proposed for generating electrical power from mechanical energy by resonance vibration of the micro beam or micro film [3-5].

Dynamics of the micro film is an important subject that should be developed. Rafael Nadal-Guardia used one-dimensional (1-D) lumped model of parallel film electrostatic transducers and studied its dynamic behavior [6]. Lu used a thin film model to interpret the thickness-dependent sum frequency generation spectra collected from the air/silica/poly (n-butyl methacrylate) /water system [7]. Akai experimentally investigated the vibration mode and transmission ultrasonic waves by pMUTs using epitaxial Pb(Zr,Ti)O₃ thin films on the epitaxial γ-Al 2O₃/Si substrates to radiate ultrasonic waves effectively [8]. Li presented an electrostatic film vibration voltage transducer [9]. Gualdino fabricated a thin-film silicon micro resonator by surface micromachining and studied vibration modes of micromechanical disk resonators made from hydrogenated amorphous silicon thin films [10]. Sorokin studied the dynamics of a circular film membrane with attached current-carrying conductors in zero gravity and calculated the spectrum of natural vibrations [11].

In a word, a number of the studies about dynamics of the micro film have been done. However, electrostatic excitation is the most frequently applied principle combining versatility and simple technology. In a MEMS device excited by the electrostatic force, the micro film is in an electromechanical-fluidic coupled field. If the clearance between the film and basement is small enough, the effects of the van der Waals force become obvious and could not be neglected. The dynamics problem of a micro film under electromechanical-fluidic-van der Waals force coupled fields has not been resolved yet.

In this paper, a multi-fields coupled dynamic equation of the micro film is presented which includes mechanical force field, the van der Waals force field, electrostatic field and fluidic damping force field. The multi-fields coupled free vibration and the amplitude frequency characteristics of the micro film are investigated. The multi-fields coupled natural frequencies of the micro film and their changes along with system parameters are discussed. A number of results are given which can be used in design and manufacture of the MEMS units.

2. Multi-fields coupled dynamics equations

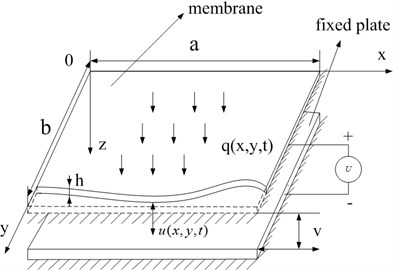
Fig. 1 illustrates a micro film under multi-fields forces. Here $u(x,y,t)=v-w(x,y,t)$, $v$ is the initial clearance between the film and fixed plate, $h$ is the thickness of the film, w is the transverse displacement of the film, a is the length of the film, $b$ is the wideness of the film, $q(x,y,t)$ is the transverse load per unit area on the film, $U$ is the voltage between the film and fixed plate.

The dynamic equation of the micro film is:

where ${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$, $\rho$ is the mass density of the film, $t$ is the time, $F$ is the tension in the film.

The electrostatic force per unit area is:

where ${\epsilon }_0$ is permittivity constant of free space, ${\epsilon }_r$ is relative dielectric constant of the insulating layer.

Fig. 1Multi-fields coupled dynamic model of a micro film

The van der Waals force per unit area between the film and fixed plate is:

where $A$ is the Hamaker constant, $A=\text{1}{\text{0}}^{\text{-19}}$ J.

The damping force per unit area from air is:

here, $c_a$ is the damping coefficient of the gas, it can be given as:

where $\mu$ is the gas viscosity, $\mu =\text{1.86×1}{\text{0}}^{\text{-5}}\text{N}\cdot \text{S}\cdot {\text{m}}^{\text{-2}}$.

Let $\epsilon =b/a$, $c_a$ can be expressed as Taylor series as below:

Neglecting high order terms, and substituting Eq. (6) into Eq. (4), yields:

Thus, the total force per unit area on the film is:

The displacement $w$ of the micro film consists of a static component $w_s$ and a dynamic one $\mathrm{\Delta }w$:

The load $q(x,y,t)$ of static ($q_s$) and dynamic ($\mathrm{\Delta }q$) components as well:

From $\mathrm{\Delta }q=\frac{dq}{dw}\mathrm{\Delta }w$, we know:

Substituting Eq. (10) into Eq. (1), yields the following equations:

3. Static displacement

Let:

here:

Let:

It should be noted that the Eqs. (15) and (16) only apply to analysis about the harmonic vibration and the weak nonlinear vibration of the film. For investigating propagating waves, transient processes, and chaotic dynamics of the film, a more complicated equation about the displacement distribution should be taken.

Substituting Eqs. (15) and (16) into Eq. (13), yields:

thus:

The average static displacement of the film is:

From Eq. (10) we know the displacement $w_s$ is included in term $q_s$. Here, we take the average displacement to replace the displacement $w_s$, and then Eq. (19) is changed into a nonlinear equation about the average displacement. From the equation, the average displacement of the film can be obtained.

4. Free vibration

Substituting Eq. (12) into Eq. (14), yields:

Let $\mathrm{\Delta }w=\varphi (x,y)q\left(t\right)$, and then substituting it into Eq. (20), yields:

where:

Letting Eq. (21) be equal to ${{\omega }_0}^2$, yields:

where:

The mode function of the micro film is considered as:

Substituting Eq. (24) into Eq. (23), yields:

From Eq. (25), we know:

From Eq. (26), the natural frequencies of the film can be given:

Using Multi-scale method, ones assume:

Substituting Eq. (28) into Eq. (22), and equating coefficients of like powers of $\epsilon$ in both sides, ones obtain:

where:

The solution of Eq. (29a) is:

Substituting Eq. (30) into Eq. (29b), yields:

where $M$ is conjugate complex of other terms.

In order to remove secular item, let:

Thus:

Substituting Eq. (33) into Eq. (31), yields:

Substituting Eqs. (30) and (34) into Eq. (29c), yields:

In order to remove secular item, let:

Thus:

Substituting Eq. (37) into Eq. (35), yields:

We know:

Substituting Eqs. (33) and (37) into Eq. (39), yields:

Letting $K\left(t\right)=1/2k\left(t\right)e^{i\theta \left(t\right)}$ and substituting it into Eq. (40), yields:

From Eq. (41), it is known:

where $k_0$ and ${\theta }_0$ is determined by initial conditions.

Substituting Eq. (42) into $K\left(t\right)=1/2k\left(t\right)e^{i\theta \left(t\right)}$, and then substituting it into Eqs. (30), (34), and (38), yields:

Substituting Eq. (43) into Eq. (28), yields:

where $\phi ={\omega }_{0}t+\theta$.

5. On linear forced response near natural frequency

Let the disturbing voltage be $\mathrm{\Delta }U=E\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{e}t\right)$, which is subjected between the micro film and the base plate. The exciting electric field force will be caused. Considering weak nonlinear influence of the above exciting electric field force, the dynamic force per unit area is changed from Eq. (12) into following form:

Substituting Eq. (45) into Eq. (14), yields:

where:

${\omega }_e$ is exciting frequency of the voltage.

Using Multi-scale method, from Eq. (46), ones can obtain the magnitude and frequency relationship of the film vibrations as below:

6. Results and discussions

Above equations are utilized for the free vibration analysis of the micro film. The parameters of the numerical example are shown in Table 1. Comparison between natural frequencies of the film is shown in Tables 2-4 and 5-7. ${\omega }_0$ is the natural frequency of the film without considering the van der Waals force, $\omega$ is the natural frequency of the film considering the van der Waals force, $\delta$ is the relative error between them. Table 2-4 gives natural frequencies of the film for various clearances between film and fixed plate (here, $F=$ 1 N, $U_0=\mathrm{}$2 V). Table 5-7 gives natural frequencies of the film for various film tensions (here, $v=$ 2 μm, $U_0=\mathrm{}$1 V).

From Tables 2-4 and 5-7, the following observations are worth noting:

1) Without considering the van der Waals force, the natural frequencies of the film vibration are larger than those of considering the van der Waals force. It is because the van der Waals force system is equivalent to a soft spring system. The van der Waals force can cause decrease of the natural frequencies of the micro film.

2) The deviation between the natural frequencies of the film with and without the van der Waals force decreases with increasing the order number of the mode. For mode(1,1) and $v=$2 μm, the relative error between the natural frequencies is 22.84 %. For mode(4,4) and $v=$ 2 μm, the relative error between the natural frequencies is 0.77 %. It shows that influence of the van der Waals force on the natural frequencies decreases with increasing the order number of the mode.

3) As initial clearance between the micro film and the base plate increases, the deviation between the natural frequencies of the film with and without the van der Waals force decreases. For mode(1,1) and $v=$ 2 μm, the relative error between the natural frequencies is 22.84 %. For mode(1,1) and $v=$3 μm, the relative error between the natural frequencies is 2.4 %.

4) As the film tension increases, the natural frequency of the film increases significantly. For mode(1,1), when the film tension grows from $F=$ 0.2 N to $F=$ 1 N, the natural frequency of the film increases by 136 %. For mode(4,4), when the film tension grows from $F=$ 0.2 N to $F=$1 N, the natural frequency of the film increases by 124 %. It shows that the film tension has obvious effects on the natural frequency of the film for various modes. As the film tension increases, the deviation between the natural frequencies of the film with and without the van der Waals force decreases slightly.

In a word, the van der Waals force should be considered for small clearance between the film and fixed plate, and small film tension.

When the exciting frequency is near the natural frequency of the micro film, changes of the vibration amplitudes with respect to exciting frequency under different modes and parameters are investigated. The results are shown in Figs. 2-5. Fig. 2 gives amplitude frequency characteristics of micro film with and without van der Waals force. Fig. 3 gives amplitude frequency characteristics of micro film for different mechanical parameters. Fig. 4 gives amplitude frequency characteristics of micro film for different fluidic viscosity. Fig. 5 gives amplitude frequency characteristics of micro film for different bias voltage. They show:

1) For mode(1,1), when van der Waals force is considered, the natural frequency of the film vibration is smaller than that without van der Waals force, but its vibrating amplitude is larger than that without van der Waals force (here, vibrating displacement peak increases by 25 % under resonance).

2) For mode(3,3), when van der Waals force is considered, both natural frequency and vibrating amplitude of the film vibration is near to ones without van der Waals force. It shows that the effects of the van der Waals force on both natural frequency and vibrating amplitude of the film become weak for high order modes.

Fig. 2Amplitude frequency characteristics under van der Waals force

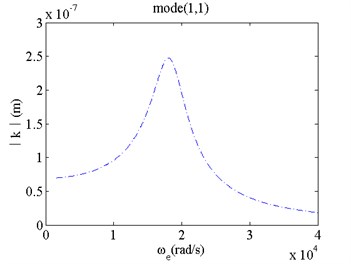
a) Mode(1,1) with van der Waals force

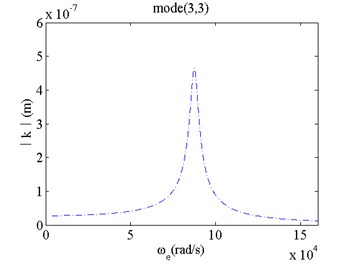
b) Mode(3,3) with van der Waals force

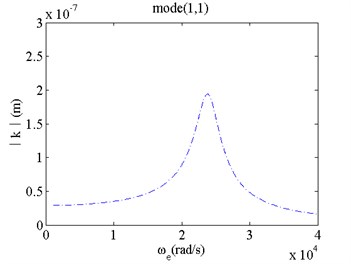
c) Mode(1,1) without van der Waals force

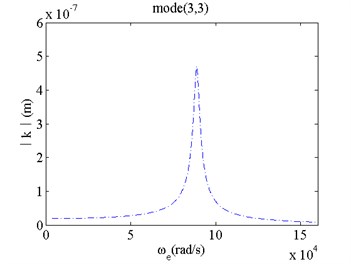
d) Mode(3,3) without van der Waals force

3) When the micro film length increases, the natural frequency of the film vibration drops and its vibrating amplitude grows. For high order modes, effects of the micro film length on the natural frequency become weak, but effects of the micro film length on its vibrating amplitude are still obvious.

4) For mode(1,1), when nonlinear parameter $\epsilon$ increases, the natural frequency and its vibrating amplitude of the film vibration drops. The resonance peak becomes smaller and smaller with increasing parameter $\epsilon$. The resonant peak of the first mode will vanish with further increasing nonlinear parameter $\epsilon$. For mode(3,3), when nonlinear parameter $\epsilon$ increases, the natural frequency and the resonance peak of the film vibration does not change nearly. When the exciting frequency deviates from the natural frequency, the vibrating amplitude of the film with a larger parameter $\epsilon$ is larger than that with a small parameter $\epsilon$.

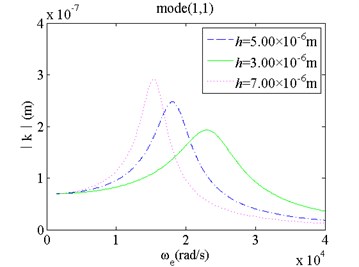
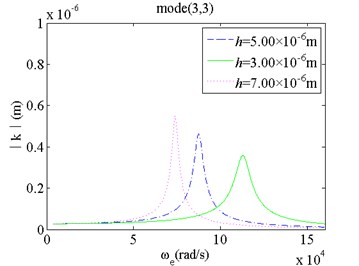
5) When the micro film thickness increases, the natural frequency of the film vibration drops and its vibrating amplitude grows significantly. For high order modes, effects of the micro film thickness on the natural frequency and its vibrating amplitude are more obvious than those for low order modes.

6) As the static voltage between the film and fixed plate increases, the natural frequency of the film vibration drops and its vibrating amplitude grows significantly. For low order modes, effects of the static voltage between the film and fixed plate on the natural frequency and its vibrating amplitude are more obvious than those for high order modes.

Fig. 3Amplitude frequency characteristics for different mechanical parameters

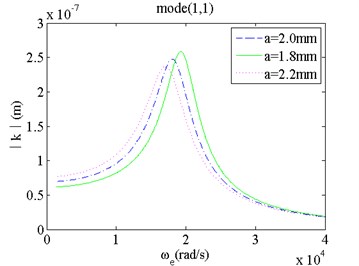
a) Mode(1,1) and $a$ changes

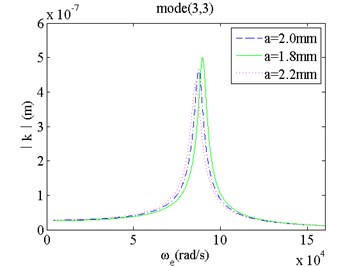
b) Mode(3,3) and $a$ changes

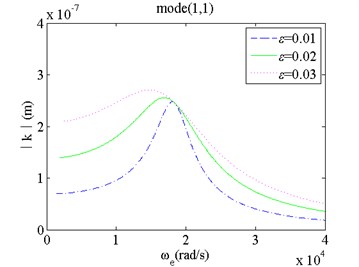
c) Mode(1,1) and $\epsilon$ changes

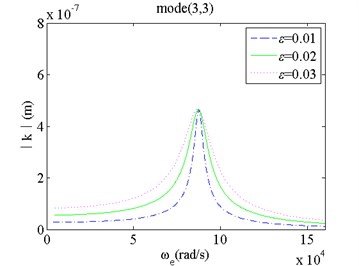
d) Mode(3,3) and $\epsilon$ changes

e) Mode(1,1) and $h$ changes

f) Mode(3,3) and $h$ changes

Fig. 4Amplitude frequency characteristics for different fluidic viscosity

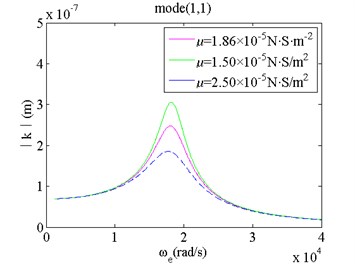
a) Mode(1,1) and $\mu$ changes

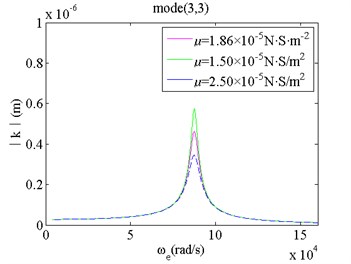
b) Mode(3,3) and $\mu$ changes

Fig. 5Amplitude frequency characteristics for different bias voltage

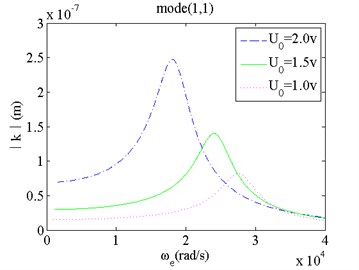
a) Mode(1,1) and $U_0$ changes

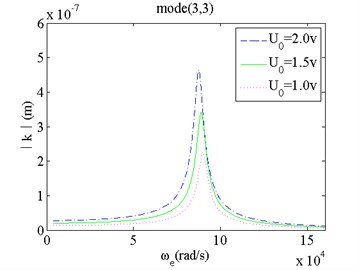
b) Mode(3,3) and $U_0$ changes

7) As the gas viscosity between the micro film and the fixed plate decreases, the vibrating amplitudes of the micro film decrease significantly. It has not nearly effects on the natural frequency of the film vibration for the high and low order modes.

In a word, the van der Waals force has obvious effects on both natural frequency and vibrating amplitude of the film for the mode(1,1); the static voltage between the film and fixed plate has obvious effects on the natural frequency for the mode(1,1) and the vibrating amplitude of the film for all of the modes; the gas viscosity only has obvious effects on the vibrating amplitude of the film for all of the modes; among mechanical parameters, the micro film thickness has obvious effects on both natural frequency and vibrating amplitude of the film for all of the modes, and the micro film length has obvious effects on both natural frequency and vibrating amplitude of the film for the mode(1,1).

7. Conclusions

In this paper, a multi-fields coupled dynamic equation of the micro film is presented. The multi-fields coupled free vibration of the micro film is investigated. The multi-fields coupled forced response of the micro film near natural frequency is analyzed. The multi-fields coupled natural frequencies of the micro film and their changes along with system parameters are discussed. Amplitude frequency characteristics of the micro film and its changes along with system parameters are given. A number of useful results are given. The results show:

1) The van der Waals force should be considered for small clearance between the film and fixed plate, small film tension, and low order modes.

2) The bias voltage between the film and fixed plate has obvious effects on the natural frequency for the mode(1,1) and the vibrating amplitude of the film for all of the modes.