Design on low noise and lightweight of aircraft equipment cabin based on genetic algorithm and variable-complexity model

Zhou, Yao-ming; Zhao, Yang; Meng, Zhi-jun

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2015

Check for updates

Design on low noise and lightweight of aircraft equipment cabin based on genetic algorithm and variable-complexity model

Yao-ming Zhou¹

Yang Zhao²

Zhi-jun Meng³

^{1, 3}School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China

²Electronic and Information Technology Department of Jiangmen Polytechnic, Jiangmen 529090, China

Corresponding Author:

Zhi-jun Meng

Cite the article Download PDF

Downloads 1071

Abstract

Aircraft equipment cabin noise will not only affect the comfort of passengers, but also affect the normal operations of the internal equipments of the aircraft, or even result in fatigue and damage to the aircraft structure itself. In the design, only to add ribs onto the panel or conduct structural-acoustic optimization on the ribs will dramatically increase the structural weight. In this paper, frequency response analysis was carried out on the structural-acoustic coupling system of the cavity panel. The cabin door panel was divided into six regions by ribs. Then, the lightweight optimization model of the cabin door panel was eventually established, with the cabin door panel thicknesses of each region and the cross-sectional areas of the ribs as the design variables, and the average sound pressure of the structural-acoustic coupling system as the constraint condition. And subsequently, the cabin door panel structure with the minimum mass and satisfying the sound pressure constraint condition was eventually obtained through genetic algorithm (GA). Moreover, so as to lighten the optimization burden, the finite element simulation model of the cabin door panel was substituted by the Kriging meta-model during the optimization process to evaluate the sound pressure response of the structural-acoustic coupling system. Furthermore, in order to narrow the difference between the meta-model and the physical one, the optimization idea of the variable-complexity model (VCM) was employed. As a result, the analysis result of the highly accurate simulation model was utilized to modify that of the Kriging meta-model. Overall, the work in this paper has an important engineering guidance value for the weight and noise reduction design of panel structure with ribs.

1. Introduction

The noise level is considered as an important index in the enclosed cavity design of aircraft. Noise will not only affect the comfort of passengers, but also affect the normal operations of internal equipments. Even worse, too loud noise will bring about fatigue and damage to the aircraft structure itself, which will finally influence the flight life and safety. For the design of the cabin door panel, on one hand, designers want to reduce the structural vibration and the radiation noise, and on the other hand, they also hope to decrease weight as much as possible under meeting the function requirements. As a result, both weight and noise reduction requirements ought to be taken into consideration in the vibration structure design [1], which could be realized through structural-acoustic optimization on the system.

There exists an obvious interdisciplinary characteristic in the structural-acoustic optimization, wherein the structural parameter variations will involve both the structure and the interaction between the structure and the acoustic field. In the optimization process, the acoustic vibration response is necessary to be analyzed. In recent years, there have been numerous researches on the structural-acoustic optimization [2], with certain achievements acquired. Luo [3]analyzed the internal acoustic field optimization of the structural-acoustic coupling system, wherein the distribution of the ribs was converted into material distribution by the topology optimization method. Lamancusa [4] utilized ANSYS to conduct numerical simulation on the acoustic response of the cubic structure, which was then modified and verified through model test. And based on this, structural-acoustic optimization was performed on the ribs of the front panel, and results were consistent with the test one. However, neither the panel thickness was optimized during the process, nor the structural mass was taken into consideration. Zhang [5-6] conducted optimization design research on the panel weight with considering the structural-acoustic coupling under the sound pressure constraint. Then, the thickness distribution of the upper panel satisfying the sound pressure constraint within the concerned frequency range was finally obtained by optimization, and a favorable reduction weight effect was achieved. Also, there were many scholars had done corresponding work on the parameter modification of the calculation model and the test verification of the optimization result [7-8]. Totally, most researches of the mentioned employed the cubic structural-acoustic coupling system with simple geometrical model in the analysis and optimization, and few were researched on structures with complicated shapes. Meanwhile, the optimization parameter was either the cross-sectional parameter of the ribs or panel thickness distribution, or else, structural mass was not taken into consideration. And there were rarely cases taking various structural parameters into account in the same time. Moreover, to better analyze the influence of material distribution on the vibration and acoustic radiation, we can divide the panel structure into many sub-regions and then perform optimization to obtain the thickness distributions of each sub-region. However, it is difficult to realize in the perspectives of technology and maintainability.

Aimed at the mentioned problems, the finite element model of the simplified equipment cabin was established. And the sound pressure response was calculated out. So as to reduce the weight under the noise constraint, the minimum structure weight was set as the objective function, and the average sound pressure inside the acoustic cavity as the constraint condition. After the optimization, the structural mass was dramatically decreased, and the noise in the cabin was restrained to a certain degree. In order to reduce the optimization burden, the finite element simulation model of the cabin door panel was substituted by the Kriging meta-model during the optimization process to evaluate the sound pressure response of the structural-acoustic coupling system. Furthermore, in order to narrow the difference between the meta-model and the physical one, the optimization idea of the variable-complexity model (VCM) was employed. As a result, the analysis result of the highly accurate simulation model was utilized to modify that of the Kriging meta-model. Overall, the work in this paper has an important engineering guidance value for the weight and noise reduction design of panel structure with ribs.

2. Sound pressure response analysis

For typical equipment cabin of the aircraft, when the cabin door closes, the radiated acoustic field resulted from vibration of the cabin door panel is mostly low-frequency noise below 500 Hz [9]. In this paper, the acoustic field inside the cabin was analyzed by the finite element method (FEM). The sound pressure coupling on the boundaries of the structure and the acoustic field were taken into account. And the finite element discretization was conducted on both the structure and the acoustic field. Meanwhile, the equation system about the structural vibration displacement and the sound pressure in the acoustic field was established, both of which could be solved once.

The wave equation of acoustic wave with small amplitude in perfect medium is as follows:

1

\nabla^{2} p + {(\frac{ω}{c})}^{2} p = 0,

wherein $p,$ $ω,$ $c$ are the sound pressure, the circular frequency and the sound velocity, respectively. The corresponding boundary condition was substituted into Eq. (1), which was then could be written in the integral form as:

2

\int_{v} δ p (\nabla^{2} p - \frac{1}{c^{2}} \ddot{p}) d v - \int_{A_{r}} δ p \frac{\partial p}{\partial n} d s - \int_{A_{a}} δ p (\frac{\partial p}{\partial n} + \frac{ρ_{a}}{Z_{a}} \dot{p}) d s - \int_{A_{e}} δ p (\frac{\partial p}{\partial n} + ρ_{a} \ddot{u}) d s = 0,

wherein $ν$ is the acoustic cavity domain, $A_{a}$ , $A_{r}$ and $A_{e}$ are the coupling boundaries of the sound-absorbing, the rigid and the elastic, respectively. $ρ_{a}$ is the density of the fluid medium. $Z_{a}$ is the acoustic impedance of the absorbing surface. Eq. (2) could be adjusted into the following form:

3

\int_{v} (L p) δ {(L p)}^{T} d v - \int_{v} \frac{\ddot{p}}{c^{2}} δ p d v - \int_{A_{r}} δ p \frac{\partial p}{\partial n} d s - \int_{A_{a}} \frac{ρ_{a}}{Z_{a}} \dot{p} δ p d s - \int_{A_{e}} ρ_{a} \ddot{u} δ p d s = 0,

wherein $L^{T} = [\frac{\partial}{\partial x} \frac{\partial}{\partial y} \frac{\partial}{\partial z}]$ . Through shape function interpolation, the parameters were dispersed, and let $p = N_{(a) i} p_{i}$ , $u = N_{(s) i} u_{i}$ , $B_{(a) i} = L N_{(a) i}$ , wherein $(a)$ and $(s)$ represent the acoustic field term and the structural one, respectively. And then Eq. (3) could be converted into:

4

\begin{matrix} \int_{v^{e}} δ p_{i}^{T} B_{(a) i}^{T} B_{(a) i} p_{i} d v + \int_{v^{e}} \frac{1}{c^{2}} δ {(N_{(a) i} p_{i})}^{T} N_{(a) i} {\ddot{p}}_{i} d v \end{matrix}

+ \int_{s_{2}^{e}} \frac{ρ_{a}}{Z_{a}} δ p_{i}^{T} N_{(a) i}^{T} N_{(a) i} {\dot{p}}_{i} d s + \int_{s_{3}^{e}} δ p_{i}^{T} ρ_{a} N_{(a) i}^{T} N_{(s) i} {\ddot{u}}_{i} d s = 0 .

The equation about coupling between acoustic field and structure is as follows:

5

M_{(a)} \ddot{p} + C_{(a)} \dot{p} + K_{(a)} p = - ρ_{a} A \ddot{u},

where:

M_{(a)} = \int_{v} \frac{1}{c^{2}} N_{(a) i}^{T} N_{(a) i} d ν C_{(a)} = \int_{s_{2}} \frac{ρ_{a}}{Z_{a}} N_{(a) i}^{T} N_{(a) i} d s K_{(a)} = \int_{v} B_{(a) i}^{T} B_{(a) i} d v A

= - \int_{s_{3}} N_{(a) i}^{T} N_{(s) i} d s,

are mass matrix, damping matrix, rigidity matrix and coupling items of the structure, respectively. They are respectively obtained through assembly of relevant element matrixes. It is shown that the coupling items are only related to shape functions of acoustic field and structure.

In the discussion above, the acoustic field equation coupled with the structure was considered. Likewise, when it comes to the coupling issue between the elastomer structure vibration and the acoustic field, according to the virtual displacement, the balance equation and the force boundary condition were denoted in the equivalent integral form. And through the variational principle, the structural dynamic equation coupled with the acoustic field could be obtained:

6

M_{(s)} \ddot{u} + C_{(s)} \dot{u} + K_{(s)} u = F_{(s)} + A_{(s)} p_{(s)},

wherein $M_{(s)},$ $C_{(s)},$ $K_{(s)},$ $F_{(s)}$ and $A_{(s)}$ are the mass matrix, the damping matrix, the stiffness matrix, the load array and the coupled matrix with the acoustic field, respectively. Note that $A^{T} = - A_{(s)}$ .

For the vibro-acoustic coupling, there is structural displacement $u$ in the acoustic space boundary condition, and sound pressure $p$ in the structural dynamic equation. As a consequence, Eq. (5) and Eq. (6) could not be solely solved. Through combination of them, the finite element equation of the acoustic-structural coupling system could be obtained:

7

[\begin{matrix} M_{a} & ρ_{a} A \\ 0 & M_{s} \end{matrix}] [\begin{matrix} \ddot{p} \\ \ddot{u} \end{matrix}] + [\begin{array}{l} C_{a} & 0 \\ 0 & C_{s} \end{array}] [\begin{matrix} \dot{p} \\ \dot{u} \end{matrix}] + [\begin{matrix} K_{a} & 0 \\ - A^{T} & K_{s} \end{matrix}] [\begin{matrix} p \\ u \end{matrix}] = [\begin{matrix} 0 \\ F_{s} \end{matrix}] .

Through the equation above, the vibration response of the elastic structure and the sound pressure in the acoustic field could be eventually obtained. When solving Eq. (7) by the numerical method, both the direct method and the modal superposition method could be employed. Due to the asymmetry and broader bandwidth of the mass matrix and the stiffness matrix, and the coupling system is equipped with more freedoms, the direct method exhibits low efficiency. Consequently, the modal superposition method was utilized for calculation in this paper.

3. Structural-acoustic optimization model based on GA and VCM and the solving flow

3.1. Structural-acoustic optimization model

With higher demands for mobility, equipment, serious requirements are put forward about vibration and noise environment of an aircraft equipment cabin. It is shown in research that radiation noise caused by vibration of plate and shell is one of the major noise sources. Noise will not only affect the comfort of passengers, but also affect the normal operations of internal equipments. Even worse, too loud noise will bring about fatigue and damage to the aircraft structure itself, which will finally influence the flight life and safety. Hence, it is very necessary to conduct optimization design to reduce vibration and noise for the plate and shell structure of equipment cabin. In this paper, the objective function of the reduction noise optimization was the minimum structural mass of the equipment cabin, and the constraint was the average sound pressure in the acoustic cavity [10]. On the basis of frequency response and sensitivity analysis of the structural-acoustic coupling system, the cabin door panel structure with the minimum mass and satisfying the sound pressure constraint was eventually designed through the optimization algorithm.

In this paper, the objective function of the optimization was that the equipment cabin had the minimum structural mass when the sound pressure met the constraint condition. Namely, we hoped to obtain a low-noise and lightweight equipment cabin. The specific mathematical model is as follows:

8

\begin{matrix} find: X = {[x_{1}, x_{2}, \dots x_{n}]}^{T}, \end{matrix}

min G = \sum_{i = 1}^{n} x_{i} A_{i} ρ, i = 1, 2, \dots, n,

p_{k} (X) \leq p_{u}, k = 1, 2, \dots, l,

x_{i l} < x_{i} < x_{i u}, i = 1, 2, \dots, n,

wherein $X$ is the design variable, $A_{i}$ is the area, length or thickness corresponding to $x_{i}$ . $ρ$ is density. $p_{k}$ is the sound pressure of node $k$ . $p_{u}$ is the upper limit of the sound pressure constraint. $x_{i u}$ and $x_{i i}$ are the upper and lower limits of the design variable, respectively.

3.2. Solving flow of structural-acoustic optimization based on GA and VCM

In this paper, the best value search method based on GA was employed to obtain the cabin door panel structure with the minimum mass and satisfying the sound pressure constraint. The genetic operation is constituted of three basic genetic operators: selection, crossover and mutation, and refer to reference [11] for details description.

During the optimization process, so as to reduce the optimization burden, the sound pressure response variable-complexity model of the structural-acoustic coupling system was established. Firstly, the Kriging meta-model was built to substitute the finite element simulation model of the cabin door panel to evaluate the sound pressure response of the structural-acoustic coupling system. Kriging meta-model is one with unbiased estimation and the minimum variance, which is characterized by local estimation through the effect of the correlation function, and refer to references [12, 13] for its mathematical description.

So as to narrow the difference between the meta-model and the physical one, the optimization idea of VCM was utilized, and the analysis result of highly accurate simulation model was employed to modify that of the Kriging meta-model. The solving flow of VCM is: (1) calculate the sound pressure responses of the coupling system at the initial point $X_{0}$ utilizing the high-accuracy and low-accuracy models, respectively. (2) Solve the scaling function, and here, the multiplication scaling function was employed, which could be calculated through Eq. (9):

9

β (X_{0}) = \frac{f_{h i g h} (X_{0})}{f_{l o w} (X_{0})} .

Fig. 1Solution flow chart of acoustic optimization

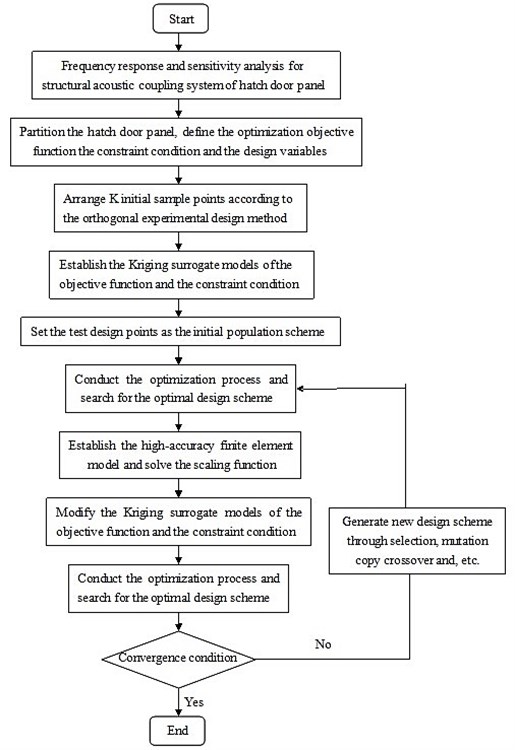
In the optimization cycle, the approximation analysis model is $f (X) = β (X_{0}) f_{l o w} (X) .$ Obviously, in $f (X)$ , the information about high-accuracy model is included, also, low-accuracy model is utilized to simplify the calculation process. (3) Conduct optimization search with the modified low-accuracy model. (4) Evaluate the optimization result with the high-accuracy model. (5) If the convergence condition is satisfied, then the calculation can terminate, otherwise, update the scaling function and re-calculate from Step 2.

The solution flow chart of the whole structural-acoustic optimization was shown in Fig. 1.

4. Optimization process and result

4.1. Geometrical model

Damping exists in all the actual structures. Due to influences from multiple factors such as technologies and boundary conditions, it is very difficult to ensure that damping of a structure applied in calculation is consistent with the actual value. As a result, the calculated results are not accurate. Hence, in this paper, damping and geometric details of structure was modified in calculation according to experimental values in order to make that the calculated values were consistent with experimental results as much as possible. It was shown in reference [13] that, through applying a modified model, the relevant responses in subsequent optimization were also be reliable.

In this paper, the ACTRAN software was utilized to calculate the sound pressure response of the structural-acoustic coupling system. And the actual equipment cabin was simplified and its finite element model was built up, with the simplified geometrical model shown in Fig. 2.

Fig. 2Simplified geometrical model

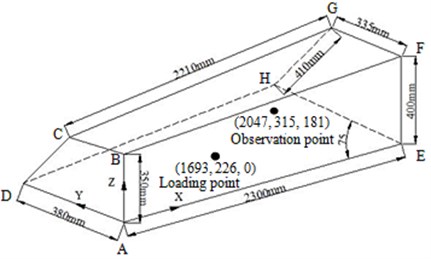
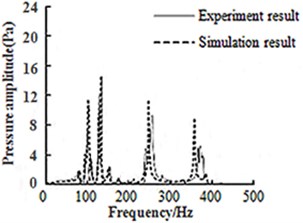
Fig. 3Comparison between simulation and experiment results

All the surfaces of the equipment cabin were simplified into elastic panels with uniform thickness. The panel material was LY12. The elastic modulus was 68 GPa. The damping was 0.01. the Poisson ratio was 0.33 and the density was 0.77 g/cm³. Moreover, the elastic shell element was employed for all the surfaces to build the finite element model, and the simply-supported boundary condition was applied on 4 edges of the cabin door panel, i.e. the displacement of the edges of AD, DH, HE and EA was 0. In Fig. 2, the panel ADHE was the cabin door panel of the equipment cabin, with the thickness of 2.0 mm, while those of other panels were all 15 mm. Additionally, Point A was the origin, AE, AD and AB were Ax is $x$ , $y$ and $z$ , respectively.

Additionally, the acoustic medium inside the cabin was the air, whose attributes at 20°C were selected as the calculation parameters, i.e. the density and the sound velocity were 1.225 g/cm³ and 340 m/s, respectively. In subsequent optimization analysis, loading points and observation points were shown in Fig. 2. Loads of the optimization design were time-domain loads. Then they were converted into values in the frequency domain through integral transformation. And then applied on loading points in the form of frequency domain load spectrum.

In order to verify feasibility of numerical algorithm and relevant simplifications, experiment was conducted for the equipment cabin. Fig. 3 showed comparison between experimental values and calculation results which were modified by parameter modification. It is shown in the figure that calculation results coincided with experimental values well. Hence, relevant simplifications and calculation method used in the paper are relatively rational. Through experimental modification, the paper obtained a finite element calculation model and relevant parameters which were consistent with the actual structure well.

4.2. Establishment of optimization mathematical model and approximation model

The face ADHE in Fig. 2 is cabin door panel of the equipment cabin with the thickness of 2.0 mm. Thickness of all the other panels for the equipment cabin is 15 mm. Hence, it is very necessary to conduct optimization to reduce vibration and noise for cabin door panel. In this paper, the cabin door panel was divided into 6 sub-regions with the ribs as the boundaries, with the corresponding thickness of $t_{1} ~ t_{6}$ , respectively. The cross-section shapes of the ribs were quadrates and the cross-sectional area of the three ribs were $A_{1}$ , $A_{2}$ , $A_{3}$ , respectively, as shown in Fig. 4.

Fig. 4Distribution diagram of cabin door panel

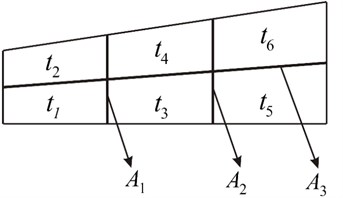
Take the thicknesses of sub-regions and the cross-sectional areas of each rib as the design variables, the average sound pressure inside the acoustic cavity as the constraint condition. The minimum mass of the whole cabin door panel structure as the objective function, and then the structural parameters of the cabin door panel were optimized, with the concrete mathematical model shown below:

10

find: X = {[x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}]}^{T},

min m,

s.t. P_{m} (D) \leq P_{m},

D_{l} < t_{i} < D_{u}, i = 1, 2, \dots, 6,

A_{l} < A_{i} < A_{u}, i = 1, 2, 3,

wherein 2.1 Pa is the upper limit of the average sound pressure inside the acoustic cavity within the concerned frequency band (here, 50 Hz~250 Hz). $D_{u} =$ 3.000 mm and $D_{l} =$ 1.000 mm are the upper and lower thickness limits of each panel, respectively. $A_{u} =$ 200 mm² and $A_{l} =$ 80 mm² are the upper and lower limits of the cross-sectional area of the ribs, respectively.

So as to establish the Kriging meta-model with high accuracy, the orthogonal test scheme of $t_{1} ~ t_{6}$ was arranged, and refer to reference [14] for the orthogonal table of the six factors.

4.3. Result and discussion

The optimization was conducted in accordance with the flow shown in Fig. 1. The population size of GA was set as 40. The maximum generation number was set as 200. The crossover probability was set as 0.7, and the mutation probability was 0.01. Additionally, each structural parameters before and after optimization were shown in Table 1.

In Section 4.2, the detailed description of each parameter in Table 1 has been made. At first, the cabin door panel was divided and arranged according to the initial values in Table 1. Afterwards, these parameters were optimized to obtain optimal values. It was shown in Table 1 that each parameter obviously decreased after the optimization, which indicated that the objective of light weight was realized. With the variables after optimization as the structural parameters, the finite element model was built to solve the sound pressure response, through which the average sound pressures inside the enclosed acoustic cavity before and after optimization could be eventually obtained, as shown in Fig. 5, wherein the frequency and the average sound pressure amplitude inside the acoustic cavity were adopted as the horizontal and vertical coordinates, respectively.

Table 1Parameters before and after optimization

Structural parameter	Initial value	Optimal value
$t_{1}$ (mm)	2.000	1.131
$t_{2}$ (mm)	2.000	1.152
$t_{3}$ (mm)	2.000	1.006
$t_{4}$ (mm)	2.000	1.101
$t_{5}$ (mm)	2.000	1.102
$t_{6}$ (mm)	2.000	1.089
$A_{1}$ (mm²)	190	95
$A_{2}$ (mm²)	190	100
$A_{3}$ (mm²)	190	94

Fig. 5Average sound pressure amplitude comparison in the acoustic cavity before and after optimizing ribs

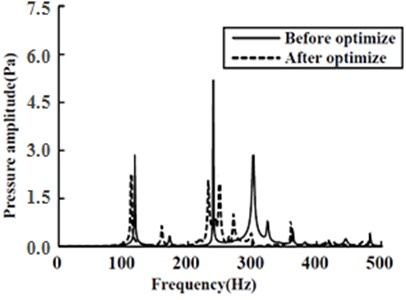
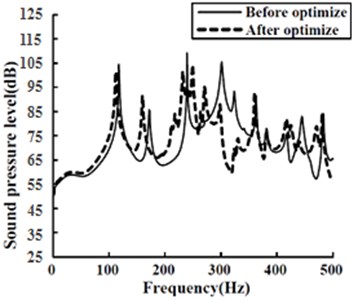
Fig. 6Average sound pressure level comparison in the acoustic cavity before and after optimizing ribs

In Fig. 5, the solid line represented the average sound pressure in the enclosed acoustic cavity of the cabin door panel with ribs before optimization, while the dashed line represented that after optimization. It can be seen from Fig. 5 that the maximum average sound pressure inside the acoustic cavity was dramatically reduced through optimization, whose amplitude was decreased from 5.3 Pa to 2.3 Pa. Overall, the sound pressure responses at the frequencies where amplitudes emerged before optimization all exhibited different degrees of reduction. Although there emerged several new amplitudes in the sound pressure response after optimization, these amplitudes were close to each other and far smaller than the maximum one before optimization. As a consequence, the reduction noise effect was favorably obvious. And the sound pressure level comparison before and after optimization was shown in Fig. 6.

It was easy to discover from Fig. 6 that through taking the logarithm, the sound pressure level exhibited a relatively low sensitivity to the variation. However, there emerged a more apparent comparison before and after optimization. As could be seen, the maximum amplitude of the average sound pressure level was reduced from 111.4 dB to 101.2 dB after optimization.

In Fig. 7, the average sound pressure amplitude comparison inside the acoustic cavities of the original structure (the cabin door panel was elastic panel with uniform thickness, no ribs added) and the optimized rib-added structure was shown.

It was easy to obtain from Fig. 7 that the average sound pressure inside the enclosed acoustic cavity was dramatically reduced after optimization relative to that of the original structure.

In order to make a clearer comparison between the acoustic responses of the optimized structure and the original one, the sound pressures were taken logarithm with respect to the standard reference sound pressure, and the sound pressure level responses were obtained, as shown in Fig. 8.

Fig. 7Sound pressure amplitude comparison between the optimized structure and the original one

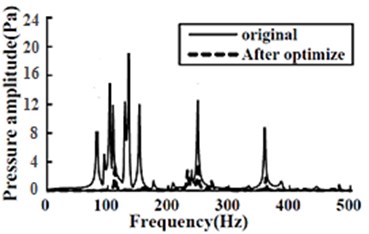
Fig. 8Comparison between sound pressure levels of the optimized structure and the original one

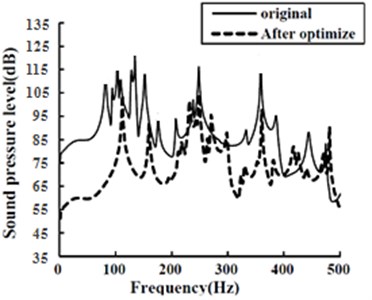
As could be seen from Fig. 8, compared with those of the original structure, the sound pressure levels at most frequencies were decreased to different degrees after optimization, especially in the low-frequency band. Additionally, the maximum sound pressure level was reduced by 19.1 dB, from 120.3 dB of the original structure to 101.2 dB of the optimized one. Overall, the reduction noise effect of the optimization in this paper met the requirements.

The optimization iteration history diagram of the design objective (the mass) was shown in Fig. 9.

Fig. 9Optimization iteration diagram for the mass of cabin door panel

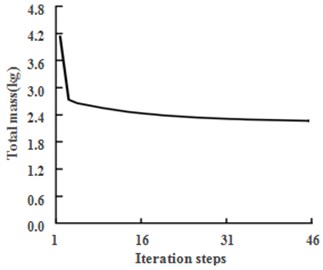
In Fig. 9, the mass variation of the whole cabin door panel (with the ribs included) during the optimization was shown. The original cabin door panel had a uniform thickness and no ribs added, whose mass was 3.221 kg, and it became 4.183 kg after the ribs added. It could be seen from Fig. 5 and Fig. 7 that through adding ribs, the average sound pressure inside the cabin was remarkably decreased, but the structural mass was dramatically increased in the meanwhile. Fortunately, this problem could be better resolved through the combination optimization on both the panel thickness and the cross-sectional area of the ribs, and the mass of whole rib-added cabin door panel was 2.531 kg after optimization, which was obviously reduced relative to the original panel, and meanwhile, the sound pressure constraint was also satisfied. Apparently, through optimization on the relative parameters, the structural mass distribution tended to be more reasonable, so did the structural dynamic stiffness distribution, thus the energy of the vibration and acoustic radiation got much lower.

Moreover, the variations of the structural parameters changed the natural vibration characteristics of the structure, thus the natural frequency of the structure got far from that of the acoustic cavity, or the modal energy close to the natural frequency of the acoustic cavity got lower, and then the coupling of the structure and the acoustic cavity was lowered, thus the noise condition was remarkably improved and the structural weight was obviously decreased in the meantime. Also, it was demonstrated that for the noise control only, the design redundancy of the original structure was relatively large and not reasonable.

5. Conclusions

In this paper, based on the structural-acoustic coupling finite element model of the enclosed equipment cabin of the aircraft, the acoustic response inside the cabin under the simplified load condition was analyzed. And subsequently, under the noise constraint, optimization design research was performed on the cabin door panel structure, wherein the cross-sectional areas of the ribs and the panel thicknesses were selected as the design variables, the minimum structural weight as the objective function, and the average sound pressure inside the acoustic cavity as the constraint. After optimization, the whole mass of the cabin door panel was decreased by 39.5 % relative to that before optimization, and the noise condition of the whole acoustic cavity was also dramatically improved, further, the maximum sound pressure amplitude was reduced from 5.3 Pa to 2.3 Pa, with the corresponding sound pressure level decreased by 9.2 %, which satisfied the noise restriction requirement. Moreover, so as to reduce the optimization burden, the variable-complexity model for the sound pressure response of the structural-acoustic coupling system was eventually established, and during the optimization process, the finite element simulation model of the cabin door panel was substituted by the Kriging meta-model to evaluate the sound pressure response of the structural-acoustic coupling system. Furthermore, in order to narrow the difference between the meta-model and the physical one, the optimization idea of the variable-complexity method (VCM) was utilized, and the analysis result of the Kriging meta-model was modified by that of the highly accurate simulation model.

References

Le Moyne S., Tebec J. L., Tawfiq I. Acoustical influence of stiffeners on acoustic radiation of plates. Mechanical Systems and Signal Processing, Vol. 19, Issue 1, 2005, p. 195-212.

Search CrossRef
Zhu D. C., Xin Y. F., Cheng W., et al. Engineering Vibration. Master Thesis, Beihang University Press, Beijing, 2004, p. 3-36.

Search CrossRef
Luo J., Gea H. C. Optimal stiffener design for interior sound reduction using a topology optimization based approach. Transactions of the American Society of Mechanical Engineers, Vol. 125, Issue 3, 2003, p. 267-273.

Search CrossRef
Lamancusa J. S. Geometric optimization of internal combustion engine induction systems for minimum noise transmission. Journal of Sound and Vibration, Vol. 127, Issue 2, 1988, p. 303-318.

Search CrossRef
Zhang J., Yao W. Z., Zhang W. Y. Optimum weight design of plate with acoustic pressure restrict for coupled acoustic-structure systems. Chinese Journal of Applied Mechanics, Vol. 23, Issue 4, 2006, p. 568-571.

Search CrossRef
Zhang J. Research on Acoustic-Structure Sensitivity and Structure-Acoustic Optimization Design. Ph.D. Thesis, Dalian Jiaotong University, Dalian, 2006.

Search CrossRef
Tinnsten M. Optimization of acoustic response – a numerical and experimental comparison. Structural and Multidisciplinary Optimization, Vol. 10, Issue 2, 2000, p. 122-129.

Search CrossRef
Marburg S., Beer H. J., Gier J., et al. Experimental verification of structural-acoustic modelling and design optimization. Journal of Sound and Vibration, Vol. 252, Issue 4, 2002, p. 591-615.

Search CrossRef
Nefske D. J., Wolf Jr J. A., Howell L. J. Structural-acoustic finite element analysis of the automobile passenger compartment: a review of current practice. Journal of Sound and Vibration, Vol. 80, Issue 2, 1982, p. 247-266.

Search CrossRef
Krog L., Tucker A., Kemp M., et al. Topology optimization of aircraft wing box ribs. 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2004, p. 1-11.

Search CrossRef
Beasley J. E., Chu P. C. A genetic algorithm for the set covering problem. European Journal of Operational Research, Vol. 94, Issue 2, 1996, p. 392-404.

Search CrossRef
Lam X. B., Kim Y. S., Hoang A. D., et al. Coupled aero-structural design optimization using the kriging model and integrated multiobjective optimization algorithm. Journal of Optimization Theory and Applications, Vol. 142, Issue 3, 2009, p. 533-556.

Search CrossRef
Laaha G., Skøien J. O., Blöschl G. Spatial prediction on river networks: comparison of top‐kriging with regional regression. Hydrological Processes, Vol. 28, Issue 2, 2014, p. 315-324.

Search CrossRef
Cai F., Xiao C., Chen Q., et al. Orthogonal test design for optimizing the extraction of total flavonoids from Flos pueraria. African Journal of Pharmacy and Pharmacology, Vol. 8, Issue 1, 2014, p. 1-8.

Search CrossRef

About this article

Received

17 August 2014

Accepted

21 February 2015

Published

30 June 2015

SUBJECTS

Vibration in transportation engineering

Keywords

lightweight design

structural-acoustic coupling

cavity

genetic algorithm

noise

variable-complexity model

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.