Abstract
To investigate the dynamic performance of the multi-span girder bridge under moving vehicles, based on the synthesis modal method, the program for vehicle-bridge coupled vibration analysis is completed firstly. According to the numerical simulation, the estimation formulas in current codes (China and UK) and some other references (USA) have been proved problematic. Also, the roughness and the critical speed are fully discussed. In addition, the DLA in the side span is largely different from that in the other span, and the DLA in other spans are almost the same. The DLA of middle span is little influenced by the number of spans. However, the DLA of side span will be stable only when the number of spans is not less than five. And when the number of spans is not more than five, the DLA of the three-span bridge is biggest, that of the five-span bridge is second, and that of the four-span bridge is smallest. It has been proved that the DLA in current code is not rational enough, as it does not distinguish the positions. It may provide some basis for the design and evaluation of the dynamic performance of bridges to moving vehicles.
1. Introduction
Due to the complexity of the vehicle-bridge coupled vibration, the dynamic effects of the bridge produced by moving vehicles are much more difficult to precisely quantify than are the static effects. McLean and Marsh [1] has indicated that loads associated with a vehicle crossing a bridge consist of the live loading resulting from the weight of the vehicle and the dynamic forces due to oscillations of the vehicle on its suspension system as well as those forces induced by the dynamic response of the bridge.
Historically, Many different terms are used for taking into account the dynamic effects of the bridge to moving vehicular loads, such as dynamic increment (DI) [2], dynamic load factor (DLF) [3], dynamic amplification factor (DAF) [4], dynamic load allowance (DLA) [5], impact factor (IF) [6] and so on. And the latter two terms are more frequently adopted. However, several authors [7, 8] have observed that the term ‘impact factor’ is too limited and therefore not descriptive of the actual behavior. Instead, the current trend is to replace the term ‘impact factor’ with ‘dynamic load allowance’, which represents the response from all types of vehicular dynamic effects, not solely impacts [1].
The dynamic response of bridges due to moving vehicles has been a subject of interest to engineers for more than 100 years. Frýba [9] had reviewed and summarized the effects of moving load on various elements, components, structures and media of engineering mechanics. Because the transport engineering structures are subjected to loads that vary in both time and space, many partial differential equations were used. Due to the over simplification of vehicles, the results may be not consistent with the actual condition, but the most important contribution is to make the basic concepts and the theory become more clearly. With the advent of the computer, a large number of researchers [10-18] tried to obtain the dynamic response using the program written by themselves. According to numerical simulations, main variables affecting bridge dynamic response are identified. Meanwhile, many fielding tests [8, 19-20] were carried out to get the dynamic load allowance or to evaluate the condition of the bridge.
However, most of them focused on the DLA in the mid-span of the girder bridge, and the influence of many parameters was studied, including of the dynamic characteristics of the vehicle, the dynamic characteristics of the bridge, and variations in the surface conditions of the bridge and approach roadways. Recently, much larger and longer bridges are completed in China. Due to the larger span and the smaller stiffness, the dynamic response of this type of bridge to moving vehicular loads is much more significant. But there is less results about it, especially on the DLA in different positions of the multi-span girder bridge with variable cross-section.
Therefore, based on a large-span continuous girder bridge named Fusui Songhua River Bridge, the dynamic load allowance in different positions of the multi-span girder bridge with variable cross-section is investigated by our own program VBCVA (Vehicle-Bridge Coupled Vibration Analysis).
2. Program of VBCVA
The vehicle-bridge coupled system consists of two subsystems, the bridge and the vehicle. When the vehicle goes across a bridge, the vibration of them will be affected by each other. Also, the position of the vehicle changes with the time. All these complicated characteristics make this problem difficult to solve, and there is still no general and public program for vehicle-bridge coupled vibration analysis up to now. Considering the advantage of existing generalized commercial software ANSYS [21] and MATLAB [22], the program VBCVA has been completed by our own research group and its accuracy has been verified [23]. Based on the modal synthesis method, the bridge model is founded by ANSYS, while the vehicle model and the roughness model are established by MATLAB.
2.1. Bridge model
According to the theory of structural dynamics, the dynamic equations for the bridge can be written as:
in which the denotes the load vector induced by the moving vehicles, , , and denote, respectively, the mass matrix, damping matrix, and stiffness matrix. Furthermore, is the displacement of the bridge, the first derivative of the displacement is the vibration velocity, and the second derivative of the displacement is the vibration acceleration. It is worth noting that all these symbols and this equation are described in Cartesian coordinate system.
As there are various types of highway bridges, and they are much more complicated with the increasing technology, the accurately modeling of the bridge may be difficult to realize by our own written program. In addition, this will hinder the generalization and the development of that program. And the limitation can be obviously seen when the equations of various types of bridges are different. Therefore, the modal synthesis method has been adopted. Another advantage of this translation is the reduction of the degree number. Then the equations of the bridge are expressed as:
where , , , and are mass matrix, damping matrix, stiffness matrix, and load vector in the modal coordinate system.
It has to be noted that the Eq. (1) is described in Cartersian coordinate system and the Eq. (2) is described in modal coordinate system. The transformation of the force can be expressed as:
where is the transposition of the matrix of mode shape.
For convenience in application, the matrix of mode shape obtained from ANSYS is normalized. Then the following matrixes are used in the program VBCVA:
where and are the damping ratio and the natural frequency of the th mode shape.
2.2. Vehicle model
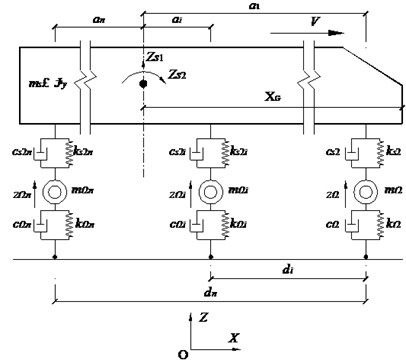
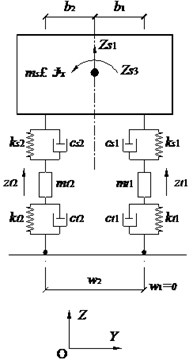
The vehicle with multi axles is adopted in this program, and the spatial model is established. The schematic plot of the vehicle model can be seen in Fig. 1.
There are some assumptions on the vehicle model. The wheel and the bridge will contact with each other all the time. Only vertical effects between the vehicle and the bridge are considered, while longitudinal and transverse effects are ignored. The vehicle body and all wheels are assumed as rigid bodies with corresponding mass, while the spring and the damper are linear. Then the vehicle equation can be given by:
in which the denotes the load vector induced by the bridge, , , and denote, respectively, the mass matrix, damping matrix, and stiffness matrix of the vehicle. Furthermore, is the displacement of the vehicle, the first derivative of the displacement is the vibration velocity, and the second derivative of the displacement is the vibration acceleration.
Fig. 1Schematic plot of the vehicle model
a) Elevation view
b) Front view
2.3. Roughness model
There are two methods to take the roughness into account, field measurement and numerical simulation. As for the former way, it is measured generally by one of the following two methods, i.e., 1) by using a profilometer; or 2) by calculating pavement roughness backwards from vibration data of the well-researched dynamic properties of the vehicle [24]. Nowadays, based on much data from the field measurement, more researchers begin to admit the fact that the roughness is a realization of a random process that can be described by a power spectral density (PSD) function. And the pavement roughness model proposed by Hwang and Nowak [10] has been adopted in this study.
Typical PSD function can be approximated by an exponential function:
in which the denotes roughness coefficient, , , , and denote, respectively, spatial frequency (m-1), lower limit, upper limit, and spectral shape index. It is assumed that the pavement roughness can be modeled as a stationary Gaussian random process. Therefore, it can be generated by an inverse Fourier transform:
where is PSD function, and is random number uniformly distributed from 0 to 2.
The process of generating pavement roughness is listed as follows:
in which the denotes the position in the longitudinal direction of the bridge, is the roughness, and is the sampling number.
2.4. Flowchart of the program
Due to various types of bridges, the modal synthesis method is adopted in the program VBCVA for general use. At first, the dynamic characteristics of the highway bridge, including natural frequencies and mode shapes, are obtained based on the finite element model (FEM) built by the commercial software ANSYS. Meanwhile, the data files for vehicles are prepared by commercial software MATLAB. Then the coupled equations are calculated using the Wilson- method. The flowchart of the program can be seen in Fig. 2.
The program can be used for calculating the cases of multi-lanes and multi-vehicles (both in longitudinal direction and transverse direction). Also, the number of axles or vehicles is not limited. Furthermore, the validity and the rationality have been verified. Therefore, this program has be thought as convenient and powerful enough for the analysis of the vehicle-bridge coupled vibration problem.
3. Numerical simulation
Based on a typical multi-span continuous girder bridge with variable cross-section and a common three-axle loading truck, the dynamic characteristics and the dynamic response in different positions of bridges with various numbers of spans are investigated by our own program VBCVA.
Fig. 2Flowchart of the program VBCVA
3.1. The multi-span girder bridge and the three-axle truck
Fusui Songhua River Bridge, total 1170 m long, is a multi-span PC (pre-stressed concrete) continuous box-girder bridge located in Heilongjiang province, China [25]. There are eight spans, 85 m+150 m×6+85 m, and the layout is shown in Fig. 3(a). It is a separate bridge with left and right parts, and the cross-section of the each part is a single cell and single box, which can be seen in Fig. 3(b). The cantilever construction method with baskets, a popular technology of large-span girder bridges, is adopted. The bridge is started in May, 2009 and completed in September, 2012 (Fig. 3(c)).
The height of the pier-top cross-section is 9.0 m and the height of the mid-span cross-section is 3.5 m. The total width is 11.25 m with 0.50 m wide and 0.75 m wide crash barrier in both sides. From the pier-top cross-section to the mid-span cross-section, the web thickness ranges from 100 cm to 55 cm, and the bottom slab thickness ranges from 150 cm to 30 cm (Fig. 3(b)). For more clearly, the simplified diagram of the bridge is shown in Fig. 3(d). And all spans are numbered from left to right.
As we know, the common number spans of large-span continuous girder bridges with variable cross-section are from 3 to 5. Therefore, in this paper, many bridges with various spans derived from the Fusui Songhua River Bridge are studied. They are listed in Table 1. It is worth noting that the only difference among these bridges is the number of spans.
In highway bridges, the types of moving vehicles are various, which is significantly different from the type of vehicles in railway bridges. Within the scope of our knowledge, the damage of the bridge is mainly produced by the loading trucks. So a typical three-axle loading truck is adopted here, and its total weight is 35 tons. The plot of the three-axle loading truck is shown in Fig. 4, and its parameters [23] are listed in Table 2.
Fig. 3Description of the bridge

a) Front view of the bridge (m)
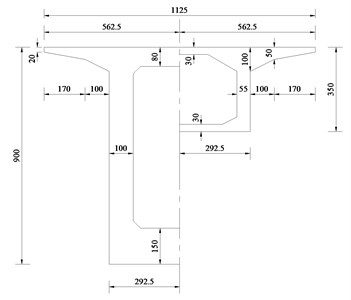
b) Cross-sections (pier-top and mid-span) (cm)

c) Actual completed bridge

d) Simplified diagram
Fig. 4The three-axle loading truck
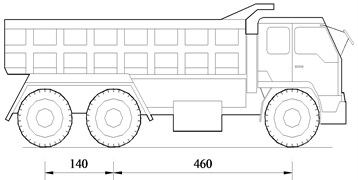
a) Schematic plot (cm)

b) Actual vehicle
Table 1List of bridges with different number of spans
Name | A | B | C | D | E | F |
No. of spans | 8 | 7 | 6 | 5 | 4 | 3 |
Layout (m) | 85+150×6+85 | 85+150×5+85 | 85+150×4+85 | 85+150×3+85 | 85+150×2+85 | 85+150+85 |
3.2. Natural frequencies of the multi-span girder bridge
Natural frequency is the fundamental dynamic characteristics of the structure, and it may be the basis of dynamic response analysis of the structure under the dynamic load, such as earthquake, wind, moving vehicles and so on. Billing [26] had pointed out that the natural frequencies of vertical bending vibration of a bridge played a major part in the response of the bridge to moving traffic loads. Also, many estimation formulas for calculating natural frequencies are obtained by massive numerical simulations [26, 27].
As for modal analysis, the spatial grillage finite element models of all these bridge samples are founded by the generalized program ANSYS. Based on the current code for bridge design in China (General Code for Design of Highway Bridges and Culverts, JTG D60-2004) [28], the first two natural frequencies are most important. In this code, the first natural frequency and the second natural frequency are used for calculating the impact factors of positive moment in mid-span section and negative moment in pier-top section respectively. Therefore, the first two natural frequencies and the corresponding mode shapes are investigated here (Table 3).
Table 2Parameters of the three-axle loading truck
Parameters | Value | Parameters | Value |
Mass of truck body | 31800 kg | Upper stiffness (front axle) | 1200 kN∙m-1 |
Mass of front wheel | 400 kg | Upper stiffness (middle/rear axle) | 2400 kN∙m-1 |
Mass of middle/rear wheel | 600 kg | Upper damping (front axle) | 5 kN s∙m-1 |
Pitching moment of inertia | 40000 kg∙m2 | Upper damping (middle/rear axle) | 10 kN s∙m-1 |
Rolling moment of inertia | 10000 kg∙m2 | Lower stiffness (front axle) | 2400 kN∙m-1 |
Distance (front axle to center) | 4.60 m | Lower stiffness (middle/rear axle) | 4800 kN∙m-1 |
Distance (middle axle to center) | 0.36 m | Lower damping (front axle) | 6 kN∙s∙m-1 |
Distance (middle to rear axle) | 1.40 m | Lower damping (middle/rear axle) | 12 kN∙s∙m-1 |
Wheel base | 1.80 m |
Table 3First two natural frequencies and corresponding mode shapes
Bridge | 1st frequency and mode shape | 2nd frequency and mode shape |
A | 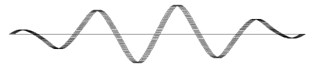 0.452 Hz | 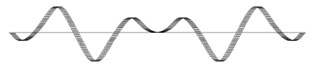 0.583 Hz |
B |  0.468 Hz |  0.635 Hz |
C |  0.494 Hz | 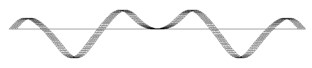 0.711 Hz |
D |  0.537 Hz | 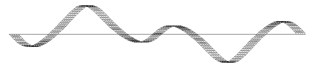 0.832 Hz |
E |  0.615 Hz |  1.046 Hz |
F |  0.785 Hz | 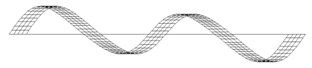 1.571 Hz |
It can be seen from the Table 3 that the first mode shape of the bridge with even spans (bridge A, C, and E) is anti-symmetrical and that is symmetrical for the bridge with odd spans (bridge B, D, and F). In addition, the natural frequencies are rising with the decreasing of the spans number, because the constraint of other spans on the middle span is increasing.
For convenient design and evaluation, the first two natural frequencies are estimated in current Chinese code (General Code for Design of Highway Bridges and Culverts, JTG D60-2004) [28]. The estimation formulas are listed as follows:
in which the denotes the main span length of the bridge, , , , and denote, respectively, the elasticity modules, moment of inertia, density, and area of the mid-span cross-section. Furthermore, and are the first two natural frequencies of the bridge. Obviously, the estimation formulas have no relation with the number of spans. So the first two natural frequencies of these six bridges are the same. The parameters of the bridge and the estimation of the first two natural frequencies are listed in Table 4.
For different bridges, the error can be obtained as follows:
where is the error of th natural frequency, is the th natural frequency calculated by ANSYS, and is the th natural frequency estimated based on the current code. The results are listed in Table 5.
Table 4Parameters of these bridges
(m) | (MPa) | (m4) | (kg/m3) | (m2) | (Hz) | (Hz) |
150 | 3.55×104 | 10.3029 | 2600 | 5.2050 | 0.501 | 0.870 |
Table 5Error of the natural frequency
Bridge | A | B | C | D | E | F |
10.88 % | –6.97 % | –1.42 % | 6.62 % | 18.51 % | 36.21 % | |
–49.21 % | –37.11 % | –22.39 % | –4.59 % | 16.84 % | 44.62 % |
It can be seen from the Table 5 that the maximum error of the first natural frequency is 36.21 %, and the maximum error of the second natural frequency is 49.21 %. In conclusion, the estimation formulas in current code are not rational enough.
As for the estimation of the natural frequency, there is less empirical formula in the existing references and codes in every country. In this paper, one of the most popular research results from USA and the current code in UK (BS5400) are selected.
Based on the regression analysis of the parametric study results, a practical equation is proposed by Barth [29] to predict the first bending natural frequency of continuous-span bridges:
where is the natural frequency from simple beam equation (Hz), and is the maximum span length (m). In addition, , , and are constant parameters. For two-span bridges, 1.44, 0.046, and 0.032. For three or more-span bridges, 1.49, –0.033, and 0.033.
In the current British code BS5400, the fundamental natural frequency can be estimated by:
where is the length of the main span (m). Additionally, is the configuration factor, which is related with the number of spans and the ratio between the side span and the middle span. But, this estimation formula will be invalid when the number of spans is more than three. Also, it has to be noted that, midspan values of and shall be used only when there is no significant change in depth or weight of the bridge throughout the span. Where the value of at the support exceeds twice, or is less than 0.8 times, the value at midspan, average values of and shall be used.
Compared the results from the USA and the UK with the numerical simulation results, they are listed in Table 6.
Table 6Comparison results of the first natural frequency
Bridge | A | B | C | D | E | F | |
(Hz) | ANSYS | 0.452 | 0.468 | 0.494 | 0.537 | 0.615 | 0.785 |
USA | 0.424 | 0.424 | 0.424 | 0.424 | 0.424 | 0.424 | |
UK | – | – | – | – | – | 1.110 | |
(USA) | 6.16 % | 9.47 % | 14.16 % | 20.97 % | 31.03 % | 46.02 % | |
(UK) | – | – | – | – | – | –41.32 % | |
It can be seen from the Table 6 that the maximum error of the first natural frequency is 46.02 % in USA, and the error in the British code is 41.32 %.
As a result, all of these estimation formulas are not sufficiently accurate. More work about the estimation of the natural frequencies has to be done in future. Therefore, these formulas should be used with caution in the design and evaluation of the highway bridge.
3.3. Vehicle-bridge coupled vibration analysis
As for the analysis of dynamic responses of the bridge under moving vehicular loads, the Fusui Songhua River Bridge and its derived bridge sample (Table 1) traversed by a three-axle loading truck (Table 2) are investigated by our own program VBCVA. Three classes of the pavement roughness are adopted, and they are named as Class I, Class II, and Class III in this paper. The maximum amplitudes of them are 1 cm, 2 cm, and 3 cm respectively, and the corresponding coefficients are 0.2345, 0.9380, and 2.1105. In addition, the speed of the moving vehicle ranges from 5 m/s to 50 m/s.
Considering the symmetry of the continuous girder bridges, only half of the bridge is analyzed. And the middle sections in every span are selected. Some of the results are plotted in Fig. 5, which are the static displacement and the dynamic displacement in the middle section of the fourth span of the bridge with the roughness of Class II under a three-axle loading truck moving at various speeds.
It can be seen from the Fig. 5 that, when the vehicle runs near the midspan of every span, the vibration of the bridge is more significant. In addition, when the speed is lower than 20 m/s, the vibration is not obvious. When the speed is 30 m/s or 40 m/s, the vibration is much larger. It may be related with the energy transformation. As we know, when the speed is higher, the kinetic energy is larger. However, due to the short period of interaction between the bridge and the moving vehicle, when the speed is high enough, the vibration of the bridge may decrease. This conclusion also can be verified in the following section.
It has been proved that [31, 32] many different definitions of dynamic load allowance are adopted by various researchers and engineers. Based on the design theory of the bridge in Chinese current code, the dynamic load allowance in this paper is defined as follows:
where is the location of the selected section, denotes the dynamic load allowance of the selected section of the bridge, and , respectively, denote the maximum dynamic response and the maximum static response of the selected section. Furthermore, and mean the location of the vehicle when the dynamic response and the static response reach the maximum value. It should be noted that and are not the same in most of time.
Firstly, the Fusui Songhua River Bridge (Bridge A) is investigated. The dynamic load allowances (DLAs) in the middle section of the 1st span, the 2nd span, the 3rd span, and the 4th span are obtained and plotted in Fig. 6.
Fig. 5Displacements of the bridge under the moving vehicle at various speeds (Class II)
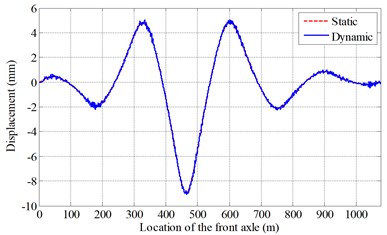
a) 10 m/s
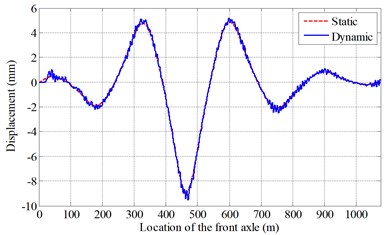
b) 20 m/s
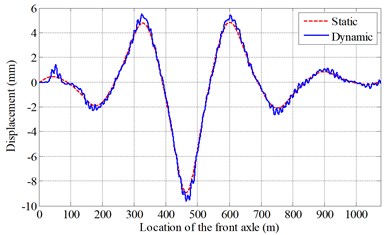
c) 30 m/s
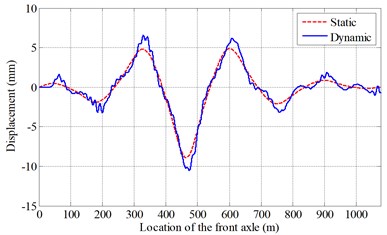
d) 40 m/s
Fig. 6DLAs in different positions of the bridge with different roughness classes
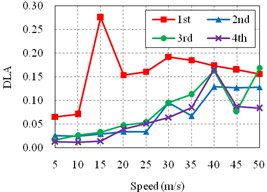
a) Roughness Class I
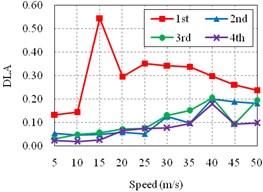
b) Roughness Class II
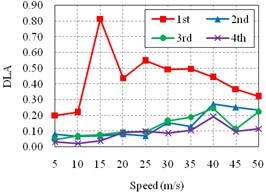
c) Roughness Class III
Fig. 6 shows that the influences of speeds on the dynamic load allowance of the bridge with different classes of roughness are similar. And the DLA is significantly increasing with the decay of the pavement roughness, which is consistent with the common understandings. In addition, the DLAs of the 2nd span, the 3rd span, and the 4th span are fluctuate ascending with the increasing of the speeds. However, the DLA of the 1st span (side span) is largely different from others. Its sensitive speed is about 15 m/s. It may be due to the quite differences of the span length and the boundary condition between the side span and other spans, which are closely related to the stiffness of the corresponding spans.
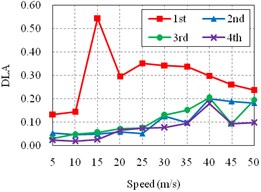
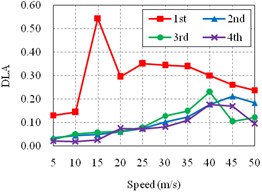
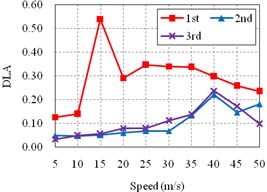
Then, the roughness is fixed as Class II. Other bridges, including of the bridge B, C, D, E, and F, are studied. And the results are plotted in Fig. 7. For convenient comparison, the results of the Bridge A (Fig. 6(b)) are also added here (Fig. 7(a)).
Fig. 7Results of different bridges under a moving three-axle loading truck
a) Bridge A
b) Bridge B
c) Bridge C
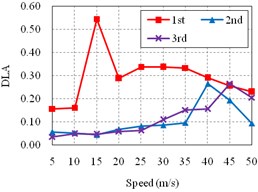
d) Bridge D
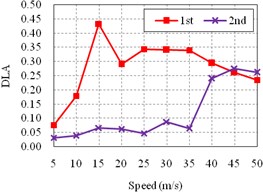
e) Bridge E
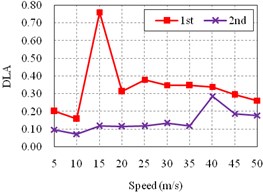
f) Bridge F
It can be seen from the Fig. 7 that, for all bridges, the DLA of side span is significantly different from the DLA of other spans, which are much more similar. Additionally, the DLA of the side span is extremely larger than others, especially when the speed is lower than 40 m/s, which is more common in actual conditions.
Finally, the influence of spans number on the dynamic load allowance of side span and middle span is studied. Also, the roughness of Class II is selected. The results are plotted in Fig. 8 and listed in Table 7.
Fig. 8Influence of spans number on DLA of the bridge
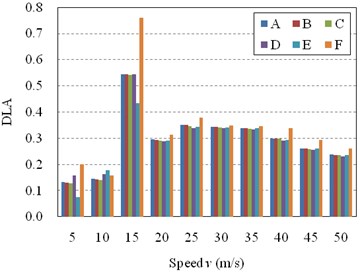
a) DLA of the side span
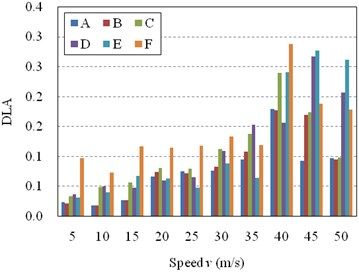
b) DLA of the middle span
It can be seen from the Fig. 8(a) that, when the vehicle is moving at the sensitive speed ( 15 m/s), the DLA in side span of the three-span girder bridge is significant larger than that of other bridges, while the DLA in side span of the four-span girder bridge is smaller than that of other bridges. However, when the vehicle is moving at other speeds, the DLA in side span of the three-span bridge is a little larger than that of other bridges, which are almost the same. In other words, the DLA in side span is not sensitive with the spans number of the bridge except for the special speed. As for the DLA in middle span of the bridge, the influence of the spans number on the DLA is not so regular (Fig. 8(b)). It can be seen that, the DLA of the three-span bridge is still much more different from that of others. When the spans number is not less than five, the DLA of middle span will be stable in most cases. Therefore, the influence of spans number on the DLA of the bridge can be ignored when the spans number is not less than five.
Table 7Influence of spans number on DLAs of the side span and the middle span
Speed (m/s) | DLA of the side span | DLA of the middle span | ||||||||||
A | B | C | D | E | F | A | B | C | D | E | F | |
5 | 0.133 | 0.131 | 0.127 | 0.157 | 0.076 | 0.200 | 0.023 | 0.021 | 0.033 | 0.036 | 0.031 | 0.096 |
10 | 0.145 | 0.143 | 0.140 | 0.162 | 0.179 | 0.158 | 0.018 | 0.018 | 0.049 | 0.049 | 0.039 | 0.073 |
15 | 0.545 | 0.544 | 0.541 | 0.545 | 0.433 | 0.760 | 0.026 | 0.026 | 0.056 | 0.047 | 0.067 | 0.117 |
20 | 0.295 | 0.294 | 0.292 | 0.288 | 0.290 | 0.313 | 0.066 | 0.073 | 0.080 | 0.059 | 0.062 | 0.114 |
25 | 0.352 | 0.350 | 0.347 | 0.339 | 0.344 | 0.379 | 0.075 | 0.072 | 0.079 | 0.064 | 0.047 | 0.117 |
30 | 0.343 | 0.343 | 0.341 | 0.337 | 0.341 | 0.348 | 0.076 | 0.082 | 0.112 | 0.109 | 0.087 | 0.132 |
35 | 0.338 | 0.338 | 0.337 | 0.333 | 0.340 | 0.346 | 0.094 | 0.108 | 0.137 | 0.152 | 0.063 | 0.118 |
40 | 0.299 | 0.300 | 0.298 | 0.291 | 0.294 | 0.340 | 0.179 | 0.177 | 0.239 | 0.156 | 0.240 | 0.287 |
45 | 0.261 | 0.260 | 0.259 | 0.256 | 0.261 | 0.294 | 0.092 | 0.169 | 0.173 | 0.267 | 0.276 | 0.187 |
50 | 0.238 | 0.237 | 0.235 | 0.230 | 0.235 | 0.262 | 0.097 | 0.094 | 0.098 | 0.206 | 0.261 | 0.178 |
4. Discussions
Based on the results obtained above, more details are deeply discussed in this section, including of the estimation of the natural frequency, the pavement roughness, the critical speed, the application of DLA in design and evaluation, and the prospect of the DLA.
1) Estimation of the natural frequency still should be noted. With the advent of computers and lots of special software, the natural frequency of every types of bridge can be easily obtained according to the finite element model. However, to get some rational and simple estimation formulas is still so important in the actual operation. Based on the estimation formulas, the influence of some parameters on the natural frequency is more clearly, and the dynamic performance of the bridge can be evaluated in concept. It may be significantly important in the phase of initial design, and it may be the guideline for the selection and determination of the bridge layout and some dimension parameters.
2) Pavement roughness cannot be neglected. All research results have proved that the roughness is the most important factor affecting the dynamic response of the bridge traversed by the moving vehicular loads. Also, when the pavement is poor, the bridge more greatly vibrates and the riding comfort is worse. As we know, the pavement is the much weaker component. So poorer pavement produces greater vibration of the bridge, and the excessive vibration of the bridge makes the pavement be seriously damaged. Then a vicious circle will be created. Especially for the rural bridges, the pavement always cannot be well maintained, which may lead much more serious damages and maintenance costs. Therefore, the pavement should be paid more attention to during the management and maintenance of the bridge.
3) The critical speed is not always high. Usually, the speed and the weight of the vehicle are decreased and limited when the technical condition of the bridge is not good enough. However, the dynamic response is not totally positive related with the speed. Additionally, the critical speeds for different positions are not the same. According to the results in this paper, the critical speed of the side span is 15 m/s. From the aspect of structural dynamics, there are three frequencies, including of the natural frequency of the bridge , the natural frequency of the moving vehicle , and the disturbance frequency which is dependent on the speed and the span length:
where is the effective span length, and is the positive integer. For simply-supported girder bridge, the effective span length is equal to the length between two supports. However, for multi-span continuous girder bridge, the effective span length means the length between two inflection points of every spans. In a word, to limit the speed in the management may be much more dangerous sometimes.
4) The application of DLA in design and evaluation should be noted. With the scope of our knowledge, the newly built bridge needs to be evaluated according to the static loading test and the dynamic loading test in most countries and states. However, there is less specific and detailed code for the dynamic loading test. As a result, the dynamic loading test is much more subjective. For example, in China, one or two parallel loading trucks are going across the bridge at various speeds in dynamic loading test. Obviously, both the number and the weight of the vehicle are not defined. In addition, the response is obtained in side span sometimes and in middle span sometimes. According to the results in this paper, the DLA in the side span is largely different from that of others. But all of these tested values are compared with the DLA in design code, which may be not rational enough. Therefore, the selection of the section should be noted during the dynamic loading test.
5) The DLA should be much more deeply investigated in future. Although there are a large number of papers and reports about dynamic load allowance, the DLA is still not unified in all over the world, even some papers or codes have produced seemingly conflicting results and conclusions. In addition, some basic concepts are still not clear enough. For example, the DLA in the design code is used for the static load model, which is not produced just by one or two vehicles, but the tested value obtained by the cases of one or two vehicles. Obviously, they cannot be compared in direct. Therefore, the DLA of the bridge duo to moving vehicles still needs more researches, which may provide the basis for the revisions of the current design and evaluation codes.
5. Conclusions
In this study, the dynamic characteristics of the multi-span girder bridge are discussed at first, and then the dynamic response of the multi-span girder bridge under moving vehicular loads is investigated by our own program VBCVA. Some conclusions are obtained as follows.
1) The natural frequencies are rising with the decreasing of the spans number, because the constraint of other spans on the middle span is increasing. The error of the estimation formulas in current design codes are much bigger sometimes, which should be highly noted.
2) The pavement roughness is the main factor affecting the dynamic response of the bridge, which should be paid more attention to during the management and maintenance of the bridge. In addition, the critical speed is not always high, especially for the side span.
3) As for the DLA in different positions, the DLA in side span is largely different from that of other spans. And the DLA of middle span is little influenced by the number of spans. However, the DLA of side span will be stable only when the number of spans is not less than five. When the number of spans is not more than five, the DLA of three-span bridge is biggest, that of five-span bridge is second, and that of the four-span bridge is smallest. So the DLA in current code is not rational enough, as it does not distinguish the positions.
Finally, the conclusions in this study may provide some basis for the design and evaluation of the dynamic performance of bridges under moving vehicles.
References
-
McLean D. I., Marsh M. L. Dynamic Impact Factors for Bridges. Transportation Research Board, Washington, 1998.
-
Cantieni R. Dynamic behavior of highway bridges under the passage of heavy vehicles. Swiss Federal Laboratories for Materials Testing and Research (EMPA), Switzerland, 1992.
-
Nassif H. H., Nowak A. S. Dynamic load spectra for girder bridges. Transportation Research Record, Vol. 1476, 1995, p. 69-83.
-
Paultre P., Proulx J., Talbot M. Dynamic testing procedures for highway bridges using traffic loads. Journal of Structural Engineering, Vol. 121, Issue 2, 1995, p. 362-376.
-
Schwarz M., Laman J. A. Response of prestressed concrete I – girder bridges to live load. Journal of Bridge Engineering, Vol. 6, Issue 1, 2001, p. 1-8.
-
O’Connor C., Shaw P. Bridge Loads: an International Perspective. CRC Press, Florida, 2002.
-
Csagoly P., Dorton R. A. The development of the Ontario highway bridge design code. Transportation Research Record, Vol. 665, 1978, p. 24-33.
-
Billing J. R., Green R. Design provisions for dynamic loading of highway bridges. Transportation research record, Vol. 950, 1984, p. 49-62.
-
Frýba L. Vibration of Solids and Structures Under Moving Loads. Thomas Telford, Scotland, 1999.
-
Hwang E. S., Nowak A. S. Simulation of dynamic load for bridges. Journal of Structural Engineering, Vol. 117, Issue 5, 1991, p. 1413-1434.
-
Li H., Wekezer J., Kwasniewski L. Dynamic response of a highway bridge subjected to moving vehicles. Journal of Bridge Engineering, Vol. 13, Issue 5, 2008, p. 439-448.
-
Wang T. L., Huang D., Shahawy M. Dynamic response of multigirder bridges. Journal of Structural Engineering, Vol. 118, Issue 8, 1992, p. 2222-2238.
-
Yang Y. B., Liao S. S., Lin B. H. Impact formulas for vehicles moving over simple and continuous beams. Journal of Structural Engineering, Vol. 121, Issue 11, 1995, p. 1644-1650.
-
Zhai W. M., Cai C. B., Wang K. Y. Numerical simulation and field experiment of high-speed train-track-bridge system dynamics. Vehicle System Dynamics, Vol. 41, 2004, p. 677-686.
-
Shi X. M., Cai C. S. Simulation of dynamic effects of vehicles on pavement using a 3D interaction model. Journal of Transportation Engineering, Vol. 135, Issue 10, 2009, p. 736-744.
-
Deng L., Cai C. S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges. Engineering Structures, Vol. 32, Issue 1, 2010, p. 21-31.
-
Yin X., Cai C. S., Liu Y., Fang Z. Experimental and numerical studies of nonstationary random vibrations for a high-pier bridge under vehicular loads. Journal of Bridge Engineering, Vol. 18, Issue 10, 2012, p. 1005-1020.
-
Arvidsson T., Karoumi R., Pacoste C. Statistical screening of modelling alternatives in train-bridge interaction systems. Engineering Structures, Vol. 59, 2014, p. 693-701.
-
Cantieni R. Dynamic load tests on highway bridges in Switzerland-60 years experience of EMPA. Swiss Federal Laboratories for Materials Testing and Research (EMPA), Switzerland, 1983.
-
Paultre P., Chaallal O., Proulx J. Bridge dynamics and dynamic amplification factors-a review of analytical and experimental findings. Canadian Journal of Civil Engineering, Vol. 19, Issue 2, 1992, p. 260-278.
-
Moaveni S. Finite Element Analysis: Theory and Application with ANSYS. Pearson Education India, Taramani, 2003.
-
Mathews J. H., Fink K. D. Numerical Methods Using MATLAB. Upper Saddle River, Prentice hall, New York, 1999.
-
Gao Q. F., Wang Z. L., Guo B. Q., Chen C. Dynamic responses of simply supported girder bridges to moving vehicular loads based on mathematical methods. Mathematical Problems in Engineering, Vol, 2014, 2014, p. 1-22.
-
Huang D. Vehicle-induced vibration of steel deck arch bridges and analytical methodology. Journal of Bridge Engineering, Vol. 17, Issue 2, 2011, p. 241-248.
-
Chen C., Mosbeh R. K., Wang Z. L., Gao Q. F., Zhong J. F. Design of a long-term monitoring system for a psc continuous box-girder bridge. Key Engineering Materials, Vol. 619, 2014, p. 1-9.
-
Billing J. R. Estimation of the natural frequencies of continuous multi-span bridges. Ministry of Transportation and Communications, Ontario, 1979.
-
Gao Q. F., Wang Z. L., Guo B. Q. Modified formula of estimating fundamental frequency of girder bridge with variable cross-section. Key Engineering Materials, Vol. 540, 2013, p. 99-106.
-
Ministry of Transport of the People’s Republic of China. JTG D60-2004 General Code for Design of Highway Bridges and Culverts. China Communication Press, Beijing, 2004.
-
Barth K. E., Wu H. Y. Development of improved natural frequency equations for continuous span steel I-girder bridges. Engineering Structures, Vol. 29, Issue 12, 2007, p. 3432-3442.
-
BSI. BS5400 Steel, Concrete and Composite Bridges, Part 2: Specification for Loads. UK, 2006.
-
Bakht B., Pinjarkar S. G. Dynamic testing of highway bridges – a review. Ministry of Transportation, Ontario, 1989.
-
Ashebo D. B. Evaluation of Dynamic Loads for Highway Bridges. The Hong Kong Polytechnic University, Hong Kong, 2006.
About this article
This work was supported by the China Scholarship Council (the 2013 China State-Sponsored Postgraduate Study Abroad Program), the National Natural Science Foundation of China (No. 51308465, No. 50678051, No. 51108132, No. U1234208) and the Fundamental Research Funds for the Central Universities (No. 2682014CX004EM). The authors would like to express their deep gratitude to all the sponsors for the financial aid.
