Abstract
Permanent magnet synchronous motor field oriented control system often uses dual-loop (speed and current) cascade structure, and the dynamics speeds of the two loops mismatch. The motor’s mechanical and electrical subsystems have the typical multirate characteristics. Based on the multirate control theory, this paper proposes multirate input quasi-sliding mode algorithm for the speed control loop. Under the situation of the output data loss, the proposed algorithm builds the extended input vector with the output prediction information. Due to the extended input vector, the proposed algorithm reduces the system steady state chatterring, and then improves the performance of the whole system. Simulation and experimental results demonstrate the effectiveness of the proposed algorithm.
1. Introduction
In recent years, permanent magnet synchronous motors (PMSMs) have been applied widely in many fields because of the attractive features such as high power density, high efficiency, high reliability etc. [1, 2]. The standard controller for a PMSM is a vector-based cascade arrangement: the speed controller (outer loop) and the current controller (inner loop).
PMSM systems are often controlled in discrete time. A controller for continuous-time systems must be converted into that for discrete-time systems by using zero-order hold (ZOH) technique. A high sampling frequency enables the acquisition of better performance as well as widening the bandwidth of the whole system. However, cascade linear controllers have a limited bandwidth in order to avoid large overshoots and ringing [3], and then the two loops are decoupled in bandwidth. It is obvious that the bandwidth of the current controller (inner) is already low resulting in a fairly modest speed control dynamic. To increase the system dynamics, multirate control methods have been reported and widely studied for achieving better performance [4-8]. In Ref. [4, 5], a multirate controller has been used in hard disk drives, with a modified state estimator. In Ref. [6], the slow rate part of multirate controller can be further decomposed and interlaced so that computation saving may be distributed uniformly at all fast rate sampling instances. In Ref. [7], multirate feedforward controller has been used in position control of DC servomotor with highly robust performance.
In practical applications, PMSM systems are always confronted with various disturbances such as parameters variations, unmodeled dynamics and load torque [9]. As a result, it is very difficult for the conventional linear control schemes to achieve high performance. In recent years, several advanced control methods have been reported that can guarantee high performance in spite of these problems [2, 10-14].
Sliding mode control (SMC) is one of the effective robust control methods since it is insensitive to parameters variations, external disturbances [2, 15-18]. Furthermore, sliding mode control for discrete-time systems (or called quasi-sliding mode control, QSMC) has attracted much attention because the implementation of the control is realized by computers with a relatively slow sampling period [19, 20]. QSMC cannot be obtained from its continuous counterpart by means of simple equivalence. Considerable efforts have been put in the analysis and design of the quasi-sliding mode control for various systems [17, 19, 21-24]. In Ref. [21] an adaptive model-free quasi-sliding mode control algorithm is proposed for nonlinear discrete-time systems, and the theoretical analysis and simulation results prove that the control algorithm can be stable and convergent. In Ref. [22] a new concept of a quasi-sliding mode control is introduced for the robust control of a PMSM system subjected to unmatched uncertainties, and the system state can be driven into a predictable neighborhood of zero. A robust discrete-time sliding mode control method on the basis of multirate output feedback has been proposed in Ref. [23].
Most of the aforementioned SMC strategies for discrete-time systems cannot take into account the difference of upgrading/sampling rate between the input and output for practical systems, especially for multirate input discrete-time systems which input upgrading speed is faster than that of the output sampling, e.g. PMSM current control loop. It is obvious that single-rate QSMC strategies would reduce the whole system dynamics owing to input upgrading speed synchronization with output sampling.
In this note, a multirate input quasi-sliding mode control (MRI-QSMC) strategy for PMSM speed control loop is proposed. In the technique, the system input is updated at a faster rate than the output. Consequently, within the speed sampling unit time, the controller takes full advantage of the extended input vector to reduce the system steady state chattering magnitude under the situation of output data loss.
2. PMSM models
Field-oriented control (FOC) and direct torque control (DTC) methods are becoming the industrial standards for motors control. Since the 70’s of last century, FOC technique was completely developed and today is mature from the industrial point of view. Unlike FOC, DTC does not require any current regulator, coordinate transformation and PWM signals generator (as a consequence timers are not required). In addition, this controller is very little sensible to the parameters detuning in comparison with FOC. On the other hand, it is well known that DTC presents some disadvantages, such as high current and torque ripple, variable switching frequency behavior, etc. In this note, PMSM control system could been built under FOC technique.
Assuming that the PMSM has negligible cross-coupling magnetic saturation, structural asymmetry, iron losses, magnet eddy current loss, and harmonics in the descriptive functions of windings, rotor anisotropy, and coercive force of magnets, the -axis equations of the PMSM are given by [25, 26]:
where are the -axis inductances (H); is the machine electrical speeds (rad/s); is the rotor inertia (kg∙m2); is the stator resistance (ohm); is the rotor flux linkage (Wb); is the machine electromagnetic torque (N∙m); is the load torque (N∙m); is the pole pair number; and are the -axis stator currents (amp.) and voltages (volts), respectively. Especially, for the surface mounted PMSM, machine the inductances are equal, assuming , is the self inductance of the motor stator. By using the field-oriented mechanism reference -axis current the machine electromagnetic torque Eq. (1c) can been simplified as:
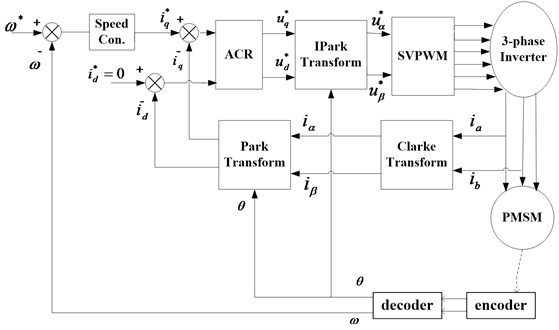
The configuration of a field-oriented control PMSM speed servo drive system is shown in Fig. 1. The system is designed for the two closed-loop (speed and current) control systems to accomplish the speed servo control of motor by the field-oriented control technology which consists of a PMSM, a SVPWM voltage source inverter, the speed controller, the automatic -axis current regulator for (ACR, PI), the encoder used to detect speed. Clarke (), Park () and Ipark () are the coordinate transformations defined as [27, 28 ]:
Fig. 1The configuration of field-oriented control PMSM speed servo drive
3. Quasi-sliding mode controller under multirate input
The speed controller is designed to get the speed to track the reference speed with highly precise and to be robust to any uncertainties and the load disturbance. is the machine mechanical speeds (rad/s), . It is assumed that the signal of the reference speed is sufficiently smooth and has the second-order derivative almost everywhere. So define the PMSM state vector as:
From Eq. (1e) and (1d), the time derivative of the state vector is:
The continuous mechanical state-space model is:
where:
Theorem 1 [29]. The pair is controllable if and only if:
where is the dimension of the state vector .
To the system Eq. (4):
so the system Eq. (4) is controllable.
Ref. [30] has proposed a novel reaching law with the terminal attractor and the system state to improve dynamics of PMSM speed servo system. The reaching law in [30] is:
where the designed parameters , , (odd number), , . It is assumed that the sliding function .
Reaching law Eq. (5) is composed of variable exponential rate () and terminal attract () reaching laws. Variable exponential rate part is the conventional exponential approach law working with power function of the state variables and the sliding mode switching function. Terminal attract part is derived from terminal attractor concept with the system state power function. With the state variables power function, the sliding mode state approach velocity is associated with the system state variables. When the control system state variables’ track is relatively far away from the sliding mode switching surface, is relatively large. Both variable exponential rate reaching law and terminal attract reaching law play a role in increasing the approaching speed. When the system state variables’ track is close to the sliding surface, due to the sliding mode function , variable exponential rate is close to zero. However, because , attracting terminal part play a major role in this process. At the same time, the sliding mode control law allows state variables moving into the sliding surface and further to the origin, and becomes increasingly smaller. Consequently, the gradual process make terminal attract part decreasing with the smaller impact rate of the system state movement to the sliding switch face. Thereby, the system state chattering is effectively suppressed.
Considering the system Eq. (4) with the reaching law Eq. (5), the control law is designed as:
The reaching and control laws are designed under the continuous-time system representation, and the sign function is not included in the law, so the chattering can be suppressed compared to the conventional sliding mode control methods. Otherwise, the discrete-time system representation is more justifiable than continuous-time for controller design due to the use of digital computers and samplers in the control circuitry. With the finite sampling frequency in QSMC, the system state trajectory is unable to move along the sliding surface, and may move about the surface, thus giving a sliding-like mode or quasi-sliding mode motion [23]. State and input chattering cannot be avoided completely in QSMC system under the finite frequency.
From the configuration of PMSM speed servo drive system Fig. 1, the current controller loop dynamics has to compromise with the modest speed, that would lead to the decrease of the whole system dynamics. In current control loop, “input” can be defined as the input -axis current (under ) to the motor, and “output” can be then defined as the motor speed . Multirate input control method is useful to increase the dynamics of the industrial systems with hardware restrictions [5, 7]. Considering the continuous PMSM mechanical system Eq. (4) to be sampled at a sampling interval of sec, the discrete-time state-space model is:
where:
Let the system input be upgraded at a interval of sec and the output be measured at a sampling interval of sec, where , being an integer. The discrete-time system state-space model sampled at the interval of sec is:
where:
From the system state-space models Eqs. (7), (8), under the multirate input mode, the system input has been extended as a -vector .
Theorem 2 [31]. Let be discretization of as in Eq. (7) under the nonpathological sampling period , then being controllable implies that is reachable.
Theorem 3 [32]. Let is controllable, with the sampling period is controllable if and only if:
where , are eigenvalues of .
In general situation, it can be easily verified that and are all reachable, which follow from Theorem 2 and Theorem 3.
From the discrete-time representation Eq. (7), we define the sliding surface function [24]:
with vector such that .
Definition 1. We call the quasi-sliding mode in the vicinity of the sliding hyperplane , such a motion of the system that:
where the positive constant is call the quasi-sliding-mode band width.
Definition 2. We say that the system Eq. (7) satisfies the reaching condition of the quasi-sliding mode in the vicinity of the sliding surface if for any the following conditions are satisfied:
where is a positive constant.
Remark. In the definition, crossing the plane is permissible, but not required.
According to the the sliding surface function Eq. (9) and the discrete-time system model Eq. (7), the reaching and control laws Eqs. (5), (6) can be represented in discrete time as:
Because , the controller output is:
Assumption 1. The system input is upgraded at a interval of sec and the output is measured at a sampling interval of sec, where , being an integer. The state should be measurable, and then is also measurable. All of the states of the subinterval of are unmeasurable.
The minimum requirements on a controller of a discrete time system is the tracking of a reference signal, i.e., , where is small. Moreover, under the limitation of output sampling rate, QSM controller takes implicitly the system extended input vector into account to increasing the convergence rate of the state. Consequently, the extended input vector can’t work without the system state information of the subinterval of .
The unmearsurable states can be predicted under the previous state and input values. The prediction process can be seen as recursive function. With the state-space model Eq. (8), the unmearsurable states estimate in Assumption 1 can be calculated as:
where:
From the control law Eq. (16) and state estimation Eq. (17), unmeasureable state point control law can be calculated as:
where is the state estimate of . For the controller output updating on the measureable state point, the PMSM multirate input state space description Eq. (8) converted into a single-rate description, where all components of the extended input are equal with . The single-rate state-space description with the sample period is:
where .
From the control law Eq. (16) and state-space description Eq. (19), measureable state point control law is:
4. Simulation results
With PMSM FOC system (Fig. 1), QSMC simulation platform is built on Matlab/Simulink. The parameters of PMSM are given in Table 1. In Fig. 1, QSMC and PI controller are used as speed regulator and current regulator (), respectively. Reference speed is 1000 r/min, the load torque is 3 N⋅m, the base period of simulation sampling is 1e-5 s.
Table 1Machine parameters
Parameters | Value |
Stator resistance (ohm) | 2.875 |
, -axis inductance (mH) | 8.5 |
Rotor inertia kg/m2 | 0.0008 |
Permanent magnet flux (Wb) | 0.175 |
Number of pole pairs | 1 |
It is first step to determine the relevant parameters of QSMC. The component of is the linear sliding surface parameter, and when the system state enters the sliding mode surface, it will affect the convergence speed of the system state. In the simulation, we set 100. and are variable exponential and terminal attract reaching law coefficients, respectively. The value of that should not be set too large, otherwise it will increase the state chattering, there 40. Other experimental parameter: 1, 2, 3, 5. The is caculated without the PMSM speed error derivative (), that mainly to avoid the interference caused by the differential term. When the sampling period is 1e-5 s, the comparision of the system response to the novel reaching law with the conventional exponential () is shown in Fig. 2, and are same as the novel reaching law.
Fig. 2PMSM system response under the novel and exponential reaching laws
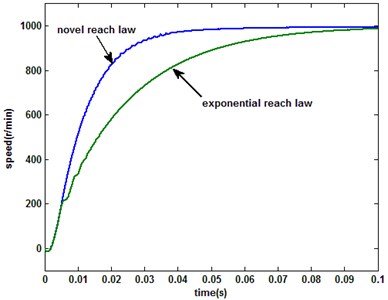
a) Speed
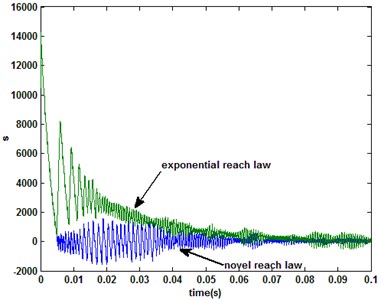
b) Sliding switch function
From the results shown in Fig. 2, it can be seen that the system performance with the novel reach law is significantly better than conventional exponential in the motor startup period. When the single-rate QSMC (the novle reach law) system is sampled with 1e-5, 2e-5 and 3e-5 s respectively, the motor speed and system sliding mode switching function are shown in Fig. 3, and the -axis currents are shown in Fig. 4.
Fig. 3PMSM system response under singlerate control mode
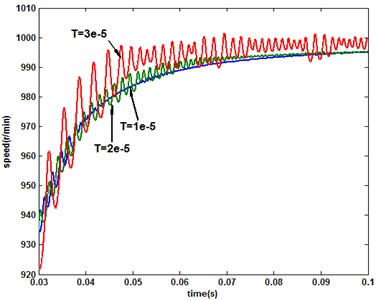
a) Speed
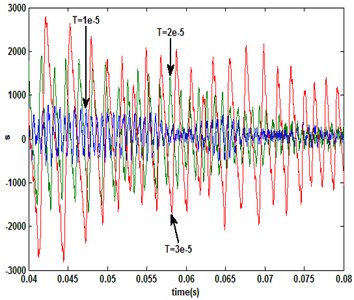
b) Sliding switch function
Fig. 4Response of iq under singlerate control mode
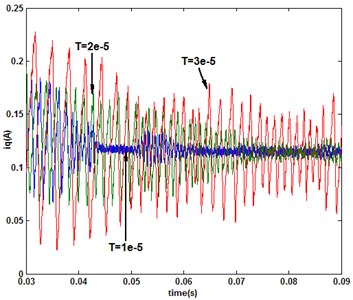
According to the results in Fig. 3, with the increase of the sampling period, the chattering of the output is exacerbated as the sliding switch function. From the -axis current response (Fig. 4), the controller output is the major cause of the state exacerbated chattering. In other words, the increase of the sampling frequency is conducive to weaken the chattering of control volume and state for QSM discrete systems. However, because of the limitations of the operating characteristics of an external device, the sampling frequency is limited dramatically, such as the optical encoder used in motor speed detection. For the measurement frequency-limited system, it is suitable to combined the multirate input control algorithm with QSMC. It is assumed that the system input and output updated/sampled periods are 1e-5 s and under multirate input control mode, respectively. And then, when 2, the responses of speed and sliding switch function under multirate and single-rate (sampling period: 2e-5 s) controllers are shown in Fig. 5. When 3 and single-rate sampling period is 3e-5 s, the comparison of system response is shown in Fig. 6.
From the results, it is can be seen that with the multirate input QSMC, the chattering magnitude of system state as sliding mode switching function is significantly weaker than the single-rate system due to the system extended input vector. Furthemore, when the single-rate system sampling period is 1e-5 s, the comparison of sliding mode switching function with multirate system is shown in Fig. 7. The results show that the multirate and single-rate systems almost have identical control effect. Otherwise, the multirate system requires less output data than the single-rate system.
Fig. 5Comparison of the response under multirate (N= 2) and single-rate (2e-5 s) QSMC
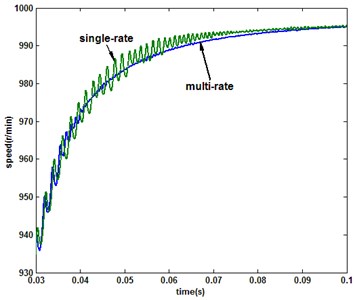
a) Speed
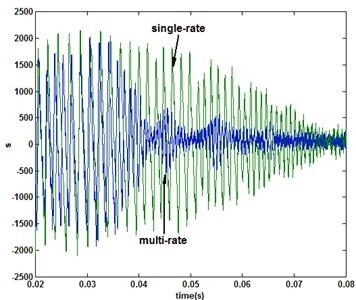
b) Sliding switch function
Fig. 6Comparison of the response under multirate (N= 3) and single-rate (3e-5 s) QSMC
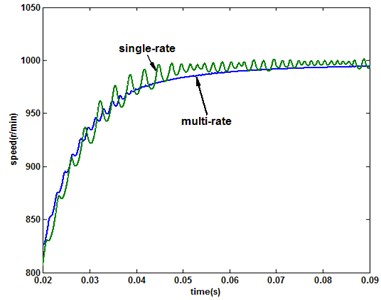
a) Speed
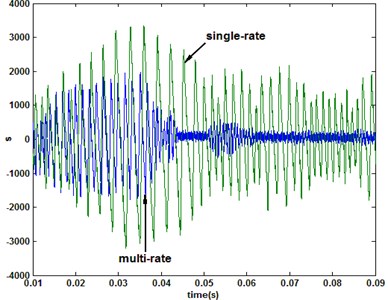
b) Sliding switch function
Fig. 7Comparison of sliding switch function under multirate and single-rate (1e-5 s) control
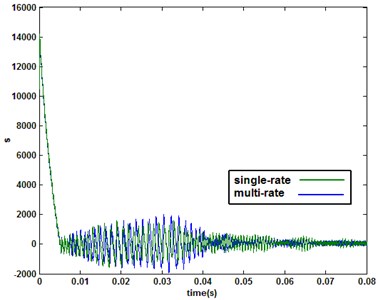
.
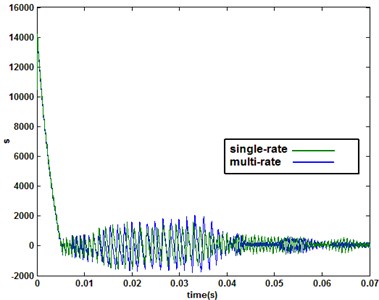
b) 3
5. Expermental results
The experimental results have been obtained with a 2.2 kW PMSM with a control board base on TMS320F2812 DSP. The overall block diagram and platform of experimental system are shown in Fig. 8 and Fig. 9, respectively.The experimental signals can be viewed in real-time with LabVIEW on the host-PC which is connected to the control board through SCI serial module.
Fig. 8Overall block diagram of PMSM’s experimental system
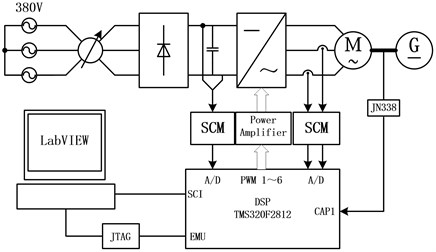
Fig. 9Experimental platform

a) Measurement and control module

b) PMSM-DC generator
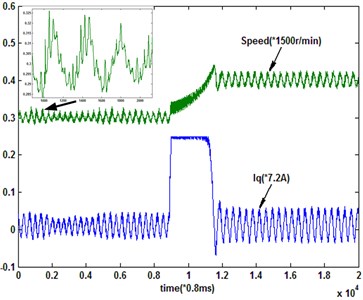
IGBT drive switching frequency is 5 kHz in the experimental system. The base period of speed contoller’s output updatding is 1.6 ms. When the sampling period is (1.6 ms), the system response under the conventional exponential reaching law is shown in Fig. 10. Under the novel reaching law, the resluts with sampling periods (1.6 ms) and (3.2 ms) are shown in Fig. 11.
From the single-rate experimental results (Figs. 10, 11), the same conclusion can be deduced with the simulation results. Comparing with the conventional exponential reaching law, the novel reaching law has shown the superiority. The increase of the sampling frequency is helpful to improve the performance of QSMC system.
Fig. 10System response under the exponential reaching law
With multirate input QSMC, the system input updating peirod is (1.6 ms) and the output sampling period is ×. When 2 and 3, the system responses are shown in Fig. 12. From the experimental results, the multirate input QSMC system ( 2) has the same performance as the single-rate system sampled with the base period (). However, the multirate input system has low output sampling frequency. Then, the performance of multirate input QSMC system ( 3) is obviously not as good as the system ( 2), because of the further expanding of unmeasurable information amount. And it is evident that the state estimation accuracy in the experimental system is worse than that in the simulation.
Fig. 11System response under the novel reaching law
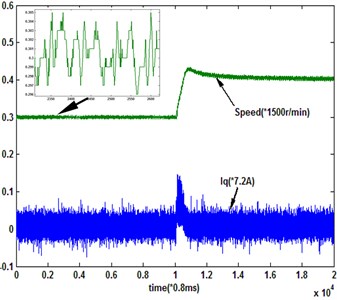
a) (1.6 ms)
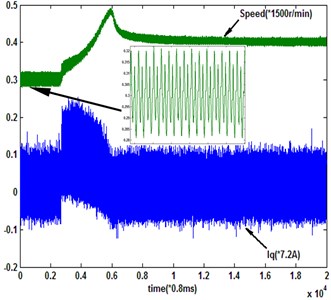
b) (3.2 ms)
Fig. 12Multirate input system response under the novel reaching law
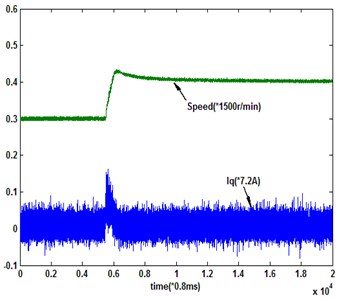
a) 2
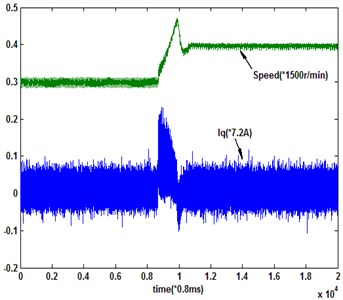
b) 3
6. Conclusion
Sliding mode control is a robust control method, sliding mode parameters match the criteria of the perturbation and external disturbances insensitivity. PMSM’s mechanical and electrical subsystems have a typical multi-rate characteristics, and with the introduction of the terminal attractor the discrete quasi-sliding mode controller for PMSM is reconstructed under multirate input control mode. Within the speed sampling cycle time, the extended input vector can play a role to reduce system steady state chatterring, and then improve the performance of the controller.
References
-
Khanchoul M., Hilairet M., Normand-Cyrot D. A passivity-based controller under low sampling for speed control of PMSM. Control Engineering Practice, Vol. 26, Issue 5, 2014, p. 20-27.
-
Qi L., Shi H. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control. Neurocomputing, Vol. 115, Issue 9, 2013, p. 23-30.
-
Preindl M., Bolognani S. Model predictive direct speed control with finite control set of pmsm drive systems. IEEE Transactions on Power Electronics, Vol. 28, Issue 2, 2013, p. 1007-1015.
-
Takeyori H., Masayoshi T. Multi-rate controller for hard disk drive with redesign of state estimator. Proceedings of American Control Conference, 1998, p. 3033-3037.
-
Hara T., Tomizuka M. Performance enhancement of multi-rate controller for hard disk drives. IEEE Transactions on Magnetics, Vol. 35, Issue 2, 1999, p. 898-903.
-
Ding J., Marcassa F., Wu S.-C., et al. Multirate control for computation saving. IEEE Transactions on Control Systems Technology, Vol. 14, Issue 1, 2006, p. 165-169.
-
Fujimoto H., Hori Y., Kawamura A. Perfect tracking control based on multirate feedforward control with generalized sampling periods. IEEE Transactions on Industrial Electronics, Vol. 48, Issue 3, 2001, p. 636-644.
-
Berg M. C., Amit N., Powell J. D. Multirate digital control system design. IEEE Transactions on Automatic Control, Vol. 33, Issue 12, 1988, p. 1139-1150.
-
Leu V. Q., Choi H. H., Jung J.-W. Fuzzy sliding mode speed controller for pm synchronous motors with a load torque observer. IEEE Transactions on Power Electronics, Vol. 27, Issue 3, 2012, p. 1530-1539.
-
Zhang B., Pi Y., Luo Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Transactions, Vol. 51, Issue 5, 2012, p. 649-656.
-
Chaoui H., Sicard P. Adaptive fuzzy logic control of permanent magnet synchronous machines with nonlinear friction. IEEE Transactions on Industrial Electronics, Vol. 59, Issue 2, 2012, p. 1123-1133.
-
Öztürk N., Çelik E. Speed control of permanent magnet synchronous motors using fuzzy controller based on genetic algorithms. International Journal of Electrical Power and Energy Systems, Vol. 43, Issue 1, 2012, p. 889-898.
-
Errouissi R., Ouhrouche M. Nonlinear predictive controller for a permanent magnet synchronous motor drive. Mathematics and Computers in Simulation, Vol. 81, Issue 2, 2010, p. 394-406.
-
Choi H. H., Jung J.-W. Takagi-Sugeno fuzzy speed controller design for a permanent magnet synchronous motor. Mechatronics, Vol. 21, Issue 8, 2011, p. 1317-1328.
-
Uktin V. I. Sliding mode control design principles and applications to electric drives. IEEE Transactions on Industrial Electronics, Vol. 40, Issue 5, 1993, p. 23-26.
-
Zhang J., Zheng W. X. Design of adaptive sliding mode controllers for linear systems via output feedback. IEEE Transactions on Industrial Electronics, Vol. 61, Issue 7, 2014, p. 3553-3562.
-
Qu S., Xia X., Zhang J. Dynamics of discrete-time sliding-mode-control uncertain systems with a disturbance compensator. IEEE Transactions on Industrial Electronics, Vol. 61, Issue 7, 2014, p. 3502-3510.
-
Orlowska-Kowalska T., Tarchala G., Dybkowski M. Sliding-mode direct torque control and sliding-mode observer with amagnetizing reactance estimator for the field-weakening of the induction motor drive. Mathematics and Computers in Simulation, Vol. 98, Issue 4, 2014, p. 31-45.
-
Gao Weibing, Wang Yufu, Homaifa A. Discrete-time variable structure control systems. IEEE Transactions on Industrial Electronic, Vol. 42, Issue 2, 1995, p. 117-122.
-
Furutak K. Sliding mode control of a discrete system. Systems and Control Letters, Vol. 14, Issue 2, 1990, p. 145-152.
-
Weihong W., Zhongsheng H. New adaptive quasi-sliding mode control for nonlinear discrete-time systems. Journal of Systems Engineering and Electronics, Vol. 19, Issue 1, 2008, p. 154-160.
-
Huang C.-F., Liao T.-L., Chen C.-Y., et al. The design of quasi-sliding mode control for a permanent magnet synchronous motor with unmatched uncertainties. Computers and Mathematics with Applications, Vol. 64, Issue 5, 2012, p. 1036-1043.
-
Janardhanan S., Bandyopadhyay B. Multirate output feedback based robust quasi-sliding mode control of discrete-time systems. IEEE Transactions on Automatic Control, Vol. 52, Issue 3, 2007, p. 499-503.
-
Bartoszewicz A. Discrete-time quasi-sliding-mode control strategies. IEEE Transactions on Industrial Electronics, Vol. 45, Issue 4, 1998, p. 633-637.
-
Underwood S. J., Husain I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines. IEEE Transactions on Industrial Electronics, Vol. 57, Issue 7, 2010, p. 2435-2443.
-
Alahakoon S., Fernando T., Trinhc H., et al. Unknown input sliding mode functional observers with application to sensorless control of permanent magnet synchronous machines. Journal of the Franklin Institute, Vol. 350, Issue 1, 2013, p. 107-128.
-
Onel I. Y., Benbouzid M. El Hachemi Induction motor bearing failure detection and diagnosis: park and concordia transform approaches comparative study. IEEE/ASME Transactions on Mechatronics, Vol. 13, Issue 2, 2008, p. 257-262.
-
Pillay P., Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Transactions on Industry Applications, Vol. 25, Issue 2, 1989, p. 265-273.
-
Antsaklis P. J., Michel A. N. Linear System. 2nd Corrected Edition. Birkhauser, Boston, 2006.
-
Xiaoguang Z., Ke Z., Li S., et al. A PMSM sliding mode control system based on a novel reaching law. Proceedings of the CSEE, Vol. 31, Issue 24, 2011, p. 77-82, (in Chinese).
-
Gu G. Discrete-Time Linear Systems: Theory and Design with Applications. Springer Science and Business Media, New York, 2012.
-
Xiao J. Multirate Digital Control Systems. Science Press, Beijing, 2003, (in Chinese).
About this article
This work was supported by the National Natural Science Foundation of China (51177137) and Chongqing City Board of Education Science and Technology Research Project (KJ130807, KJ1400924).
