Asynchronous vibration response characteristics of connectors with looseness fault and its verification

2.1. A single disk-rotor model

The differential equations of the unbalance response of a single disk mounted on a massless shaft can be described as follows:

where $u$ and $v$ are the displacements of the rotor, $m$ is the mass of the disk, $c$ is the viscous damping, $k$ is the transverse stiffness of the shaft, $e$ is eccentricity, and $\omega$ is rotational speed of the rotor.

2.2. A foundation looseness model

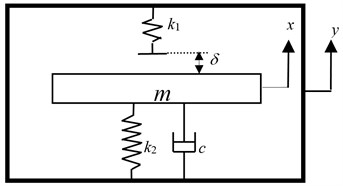
In order to study the mechanism of the looseness fault between component and foundation, a simple mass-spring model with looseness fault is established, and the mass block is always connected with the foundation, as shown in Fig. 1.

It is assumed that the mass of mass block is $m$, the contact stiffness between the mass block and the foundation is $k_2$, the damping is $c$, the contact stiffness between the mass block and the hard spring is $k_1$; the looseness clearance is $\delta$, the vibration displacement of the mass block is $x$, and the vibration displacement of the foundation is $y$.

The differential equation of the mass block under the foundation vibration can be described as follows:

Fig. 1Mass and foundation looseness model sketch

The contact stiffness between the mass block and the foundation under the conditions of different relative displacements can be described as follows:

It is assumed that vibration frequency of the foundation is $f$, the amplitude is $A$, the vibration displacement of the foundation $y=A\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi ft\right)$, and the relative displacement between the mass block and the foundation $z=x-y$. The relative motion equation can be described as follows:

Since the second formula of Eq. (1) is similar to Eq. (4), and the looseness fault has directivity, which means the vibration in $x$ direction and in $y$ direction are separable, Eq. (4) can be used to simulate the looseness fault of single disk-rotor model. The relative displacement $z$ can be used to simulate the displacement of rotor and the relative acceleration $\ddot{z}$ can be used to simulate the acceleration of rotor.

Then, the natural frequency of the hard spring $f_1={\left(\left(k_1+k_2\right)/m\right)}^{1/2}$ and the natural frequency of the soft spring $f_2={\left(k_2/m\right)}^{1/2}$. It is assumed that the natural frequency of the system is $f_n$; the clearance $\delta$ is smaller, the vibration time is very short, and it can be ignored, so that the vibration period of this system is half of the sum of the vibration period of the hard spring and the soft spring, it can be described as follows:

2.3. Simulation analysis of looseness fault

For studying the strong nonlinear characteristics caused by the looseness fault, smaller damping and larger stiffness are adopted. It is assumed that the mass of the mass block $m=$ 10 kg, the vibration amplitude of the foundation $A=$ 100 µm, the damping between the mass block and the foundation $c=$ 20 N·s/m, the contact stiffness $k_2=$ 9.85×10⁵ N/m, and the contact stiffness $k_1$ between the mass block and the hard spring is 100$k_2$. The natural frequency of this system, according to the Eq. (5), $f_n=$ 90.9 Hz. The response of this system is solved by the improved Newmark-$\beta$ algorithm [13]. When the hard spring is contacted, the contact condition is marked 1, otherwise the contact condition is marked 0.

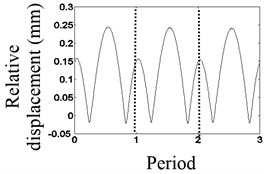
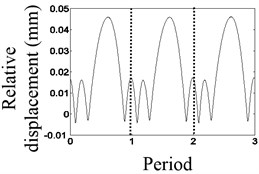
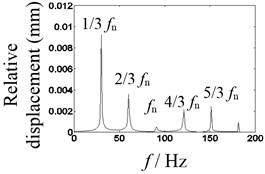
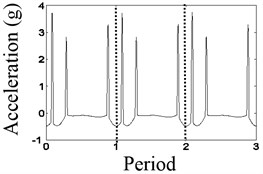
The results are shown in Figs. 2, 3, when the vibration frequencies are 1/2$f_n$ and 1/3$f_n$, respectively. In Fig. 2(a), the waveform of relative displacement has two bounces and two peaks per revolution. In Fig. 2(b), the rotational frequency and the larger double frequency appear in the spectrum of the relative displacement. In Fig. 2(c), the acceleration of the mass block has two bounces per rotation. In Fig. 3(a), the waveform of the relative displacement has three bounces and three peaks per revolution. In Fig. 3(b), the rotational frequency, the larger double frequency and the natural frequency of the system appear in the spectrum of the relative displacement. In Fig. 3(c), the acceleration of the mass block has three bounces per rotation. As shown in Figs. 2(c), 3(c), the changing period of stiffness is equivalent to the period of the rotating speed, so that frequency multiplication components appear.

Fig. 2Waveform characteristics at 1/2 times the natural frequency

a) Waveform

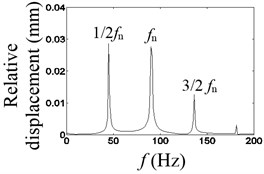
b) Spectrum

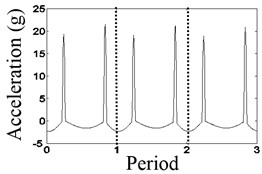
c) Waveform

Fig. 3Waveform characteristics at 1/3 times the natural frequency

a) Waveform

b) Spectrum

c) Waveform

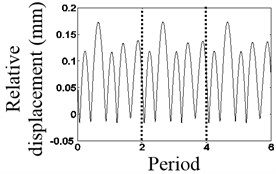
The results are showed in Figs. 4-6 when the vibration frequencies are 2/5$f_n$, 3/7$f_n$ and 4/9$f_n$, respectively. In Fig. 4(a), the waveform of the relative displacement has five bounces and five peaks every two revolutions. In Fig. 4(b), the rotational frequency, the larger asynchronous frequency and the natural frequency of the system appear in the spectrum of the relative displacement. In Fig. 4(c), the changing period of stiffness is equivalent to twice the period of the rotating speed, so that 1/2× component appears. In Fig. 4(d), the waveform of the relative acceleration of the mass block has five shocks every two rotations.

In Fig. 5(a), the waveform of the relative displacement has seven bounces and seven peaks every three revolutions. In Fig. 5(b), the rotational frequency, the larger asynchronous frequency and the natural frequency of the relative displacement appear in the spectrum. In Fig. 5(c), the changing period of stiffness is equivalent to three times the period of the rotating speed, so that 1/3× component appears. In Fig. 5(d), the waveform of the relative acceleration of the mass block has seven shocks every three rotations.

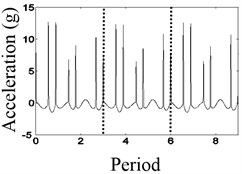
In Fig. 6(a), the waveform of the relative displacement has nine bounces and nine peaks every four revolutions. In Fig. 6(b), the rotational frequency, the stronger asynchronous frequency and the natural frequency of the relative displacement appear in the spectrum. In Fig. 6(c), the changing period of stiffness is equivalent to four times the period of the rotating speed, so that 1/4× component appears. In Fig. 6(d), the waveform of the relative acceleration of the mass block has nine shocks every four rotations.

As can be seen from Figs. 2-6, the natural frequency and asynchronous frequency components are excited. When the rotational frequency equals to 1$/J$ ($J=$ 1, 2…) the natural frequency of system, that is, the changing period of stiffness is equal to the period of the rotating speed, frequency multiplication components appear. When the rotational frequency is equal to $J/(\text{2}J+\text{1})$, $(J+\text{1})/(\text{2}J+\text{1})$, $(\text{2}J-\text{1})/\left(\text{2}J\right)$ ($J=$ 2, 3…) the natural frequency of system, the changing period of stiffness is equal to $n$ times the period of the rotating speed, then 1$/n$ frequency division components appear, and the natural frequency of system is excited.

Fig. 4Waveform characteristics at 2/5 times the natural frequency

a) Waveform

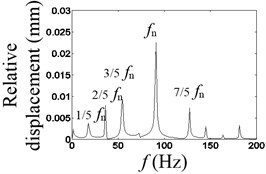
b) Spectrum

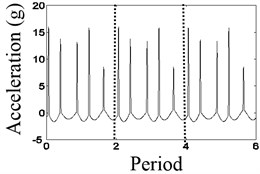
c) Waveform

Fig. 5The waveform characteristics at 3/7 times the natural frequency

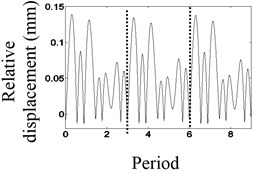
a) Waveform

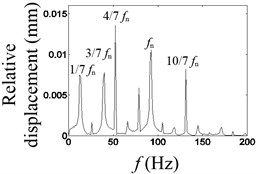
b) Spectrum

c) Waveform

Fig. 6The waveform characteristics at 4/9 times the natural frequency

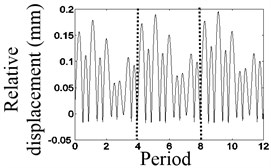
a) Waveform

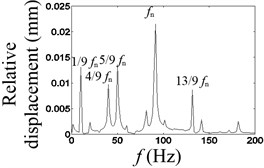
b) Spectrum

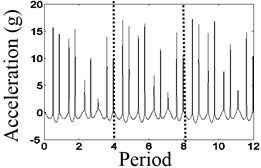
c) Waveform

Fig. 7Campbell diagram showing under subcritical speeds

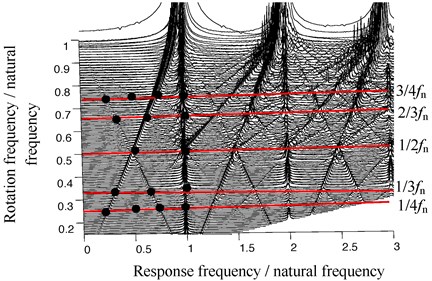
The Campbell diagram of rotor acceleration at the subcritical speeds is shown in Fig. 7. As can be seen from Fig. 7, the looseness fault characteristics are shown as the crossed streaks in the Campbell diagram, which are the asynchronous response frequencies. When the rotational frequencies are 1/4$f_n$, 1/3$f_n$ and 1/2$f_n$, frequency multiplication components will appear. When the rotational frequency is 2/3$f_n$, 1/2× and the frequency multiplication components will appear. When the rotational frequency is 3/4$f_n$, 1/3×, 2/3× and the frequency multiplication components will appear. Such similar phenomenon also appears at the transcritical and supercritical speeds.

3.1. Connector looseness experiment principle

In order to verify the non-synchronous response characteristics of connector looseness fault, the experiment rig with looseness clearance was established, and the connector looseness experiment was carried out. Fig. 8 is the experimental site map of looseness fault. Fig. 9 is the experimental three-dimensional diagram of looseness fault.

Fig. 8The experimental site map of looseness fault: 1 – computer; 2 – NI USB-9234 data acquisition card; 3 – vibration controller; 4 – power amplifier; 5 – the first disk; 6 – the second disk; 7 – the third disk; 8 – acceleration sensor (B&K4508); 9 – acceleration sensor for controller; 10 – vibrating table

Fig. 9 shows that the second disk is connected to the third disk by spring $k_1$, the third disk is connected to vibrating table by bolts, and the first disk is connected to the third disk by using three polish rods. Then the first disk, the third disk and vibrating table will vibrate together. The first disk and the second disk are connected by spring $k_2$, and the connector looseness fault is simulated by controlling the clearance.

Fig. 9Experimental three-dimensional diagram of looseness fault

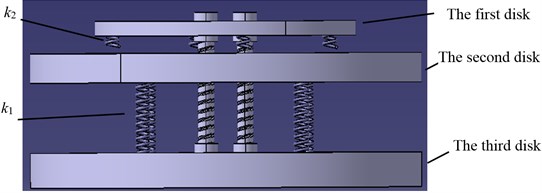
During the experiment, the first disk, the third disk and vibration table vibrate together, and the basement excitation to the second disk is carried out. When the relative displacement between the second disk and the third disk is smaller, the spring $k_2$ does not connect with the second disk, so the spring connection stiffness is only $k_1$. When the relative displacement between the second disk and the third disk is larger, the spring $k_2$ connects with the second disk, so the spring connection stiffness is $k_1+k_2$.

The energy of vibrating table was input by power amplifier, and the feedback of vibration signals was realized by controlling the software and the vibration acceleration sensor on the third disk. The vibration of the vibrating table was controlled at the designated frequency and amplitude by vibration controller. The vibration acceleration of the second disk was measured by the vibration acceleration sensor on the second disk. The collected digital signals were input into the computer for preservation by NI USB-9234 capture card.

In order to obtain the vibration performance of the vibration system, the excitation on vibrating table was applied by using the linear sine sweep frequency method from 5 Hz to 100 Hz, and the looseness fault characteristics at different frequencies were obtained.

3.2. Looseness fault experiment verification

3.2.1. Analysis of the second disk response at different contact forms

In the experiment, the acceleration of the second disk are measured by three methods, namely: 1) when the second disk does not contact with the spring $k_2$, the second disk only contacts with the third disk through spring $k_1$, the vibration system is a liner system, and the experiment result is shown in Fig. 10(a); 2) when the second disk always contacts with the spring $k_2$, the second disk contacts with the third disk and the first disk through spring $k_1$ and $k_2$, the vibration system is also a liner system, its spring connection stiffness is $k_1+k_2$, and the experiment result is shown in Fig. 10(b); 3) when there is clearance between the second disk and spring $k_1$, at different relative vibration displacement between the second disk and the first disk, the second disk may contacts with spring $k_1$ or not, the vibration system is a nonliner system, and the experiment result is shown in Fig. 10(c).

Fig. 10(a) shows that when the second disk does not contact with the spring $k_2$, the vibration system is a liner system, and its natural frequency is 14.6 Hz. Fig. 10(b) shows that when the second disk always contacts with the spring $k_2$, the vibration system is also a liner system, and its spring connection stiffness is $k_1+k_2$, so its natural frequency is 51.22 Hz. When there is looseness clearance, the second disk may contacts with spring $k_1$ or not. According to Eq. (5), the calculated result $f_n$ is 22.7 Hz, and the experimental result is 22.2 Hz, shown in Fig. 10(c). Obviously, the analysis results are verified fully.

Fig. 10The response of the second disk under different contact conditions

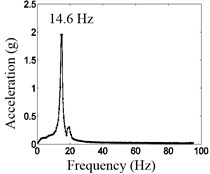
a) No contact between the second disk and spring $k_2$

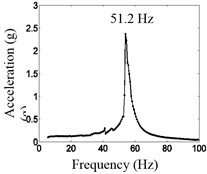
b) Always contact between the second disk and spring $k_2$

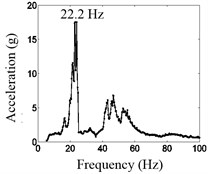
c) Discontinuous contact between the second disk and spring $k_2$

3.2.2. Analysis of looseness characteristics

In order to highlight the period components of vibration frequency, frequency multiplication and frequency division in system, autocorrelation method is used to denoise the acceleration signal of the second disk.

Fig. 11 is cascade plot of the second disk vibration acceleration changing with excitation frequency and response frequency. Fig. 11 shows that the frequency multiplication appears when excitation frequency is 1/2$f_n$, 1/2 frequency division appears when excitation frequency is 2$f_n$, and 1/3 frequency division appears when excitation frequency is 3$f_n$.

Fig. 11Cascade plot of the second disk response

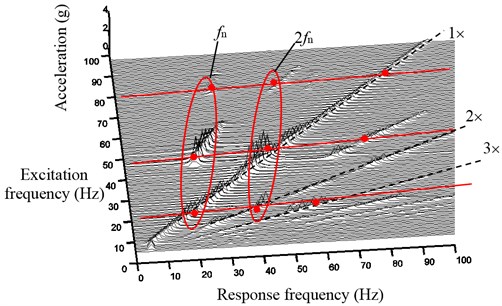
Fig. 12 shows time domain waveform before and after the noise reduction and spectrum before the noise reduction of the second disk when the excitation frequency is 12.5 Hz. As shown in Fig. 12, when the excitation frequency is equivalent to 1/2$f_n$, the larger double frequency components appeared, that is the natural frequency of the system.

Fig. 13 shows time domain waveform before and after the noise reduction and spectrum before the noise reduction of the second disk when the excitation frequency is 45 Hz. As shown in Fig. 13, when the frequency of the vibration table is equivalent to 2$f_n$, the larger 1/2 dividing frequency components appeared, that is the natural frequency of the system.

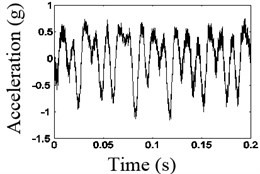
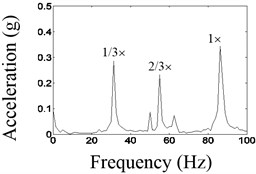
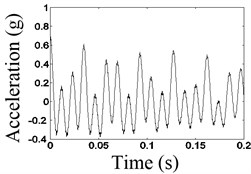
Fig. 14 shows time domain waveform before and after the noise reduction and spectrum before the noise reduction of the second disk when the excitation frequency is 80 Hz. As shown in Fig. 14, when the frequency of the vibrating table is about 3$f_n$, the larger 1/3 dividing frequency components appeared, that is the natural frequency of the system.

As shown in Figs. 12-14, the waveforms after the noise reduction have the characteristics that is a typical shock characteristic, with the waveform of truncated shape, which is longitudinal asymmetrical.

Fig. 12Waveform and frequency spectrum before and after the noise reduction when frequency is 1/2fn

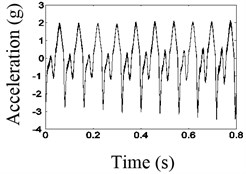
a) The waveform before noise reduction

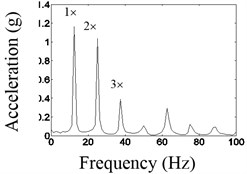
b) The spectrum before noise reduction

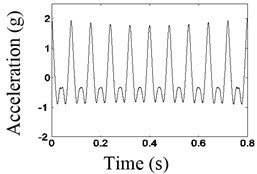
c) The waveform after noise reduction

Fig. 13Waveform and frequency spectrum before and after the noise reduction when frequency is 2fn

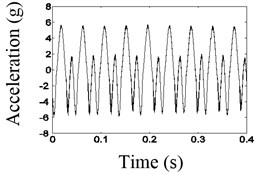
a) The waveform before noise reduction

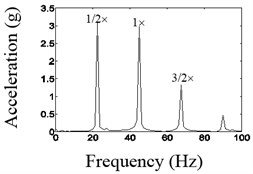
b) The spectrum before noise reduction

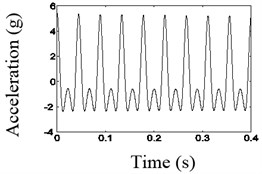
c) The waveform after noise reduction

Fig. 14Waveform and frequency spectrum before and after the noise reduction when frequency is 2fn

a) The waveform before noise reduction

b) The spectrum before noise reduction

c) The waveform after noise reduction

By comparison, in different frequencies of the vibrating table, for connector looseness fault, the acceleration waveforms after the noise reduction of autocorrelation have the characteristic that is a typical shock characteristic, with the waveform of truncated shape, which is longitudinal asymmetrical, which could be identified as the characteristics of the looseness fault.