A hybrid training method for ANNs and its application in multi faults diagnosis of rolling bearing

2.1. Traditional training methods

The most common training method of the feedforward ANNs is gradient descent which performs steepest descent on a surface in weight space whose height at any point in weight space is equal to the error measure [3]. Gradient descent method is simple and easy to implement, it can be an efficient method for obtaining the weight values that minimize an error measure, and error surfaces frequently possess properties the make this procedure slow to converge. Several heuristics were proposed that provide guidelines for how to achieve faster rates of convergence than steepest descent techniques. Momentum implements the heuristics through the addition of a new term to the weight update equation [19]. A learning rate update rule that performs steepest descent on an error surface defined over learning rate parameter space implements the heuristics [20].

In most application of ANNs, there are often a large amount of weights need to be optimized. Although these algorithms based on the gradient descent are well known in optimization theory, they usually have a poor convergence rate and depend on parameters which have to be specified by the user. A quadratic convergent gradient method (Conjugate Gradient) is proposed to achieve faster convergence. The method is best able to deal with complex situations such as the presence of long curving valley. And the oscillatory behavior characteristic of methods such as steepest descents is thereby avoided [21].

The Levengerg-Marquardt algorithm is an approximation to Newton’s method. The key step in this algorithm is the computation of the Jacobian matrix. For the neural network mapping problem the terms in the Jacobian matrix can be computed by a simple modification to the backpropagation algorithm. And the LM algorithm can be considered a trust-region modification to Gauss-Newton, it is also easy to implement [5].

2.2. DE method

Differential evolutionary algorithm are used to perform various tasks, such as connection weight training, architecture design, learning rule adaption, and connection weight initialization from ANN’s, but mostly for connection weight training [22]. DE can be referred as heuristic optimization algorithms which are simple and intuitive, without a priori knowledge of the problem, and widely used in application. In [23], the differential evolution was first used to train the neural network, and got good convergence properties. The core process of DE contains three operations like GA, and they are mutation, crossover and selection [24].

The most common fitness function (or error function) is mean-square error (MSE), although in some situations other error criteria may be more appropriate [25]:

where constant $M$ is the length of output vector of the network, $T_j$ is the $j$th parameter of target output vector, and $O_j$ is the $j$th parameter of network output vector.

In [26], during experiments between variants of DE, DE/rand/1/either-or performs both fast and reliable. In which, the mutant vector is generated according to:

From experience $K=\text{0.5}(F+\text{1})$ can be recommended as a good first choice for $K$ given $F$. Probability constant $P_F$ is introduced to implement a dual-axis search. The scheme accommodates functions above that are best solved by either mutation only ($P_F=$0) or recombination only ($P_F=$1), as well as generic functions that can be solved by randomly interleaving both operations (0$<P_F<$1).

3.1. Probabilistic adaptive strategy

The DE-LM algorithm that combined DE and LM is one of hybrid methods combined heuristic method with traditional method. It trains the target vector twice, first in the process of DE to reach a basin global minimum point, and then in the process of LM to increase the convergence. It shows that the hybrid method could well solve the complex problems like nonlinear system identification [11]. In the scheme, it needs more time to complete process from one generation to the next generation.

For most problems, the convergence speed of the DE is very high at the moment of starting, as the solution approaches to the global minimum the convergence speed automatically changes to a low value. Mention that the LM method is used to reach faster rate of convergence, so during the initial period, the process of LM method should not be proceeded, then the time used in a single iteration would be reduced. Furthermore, the decrease using LM method could reduce the risk that the population would be lead to a local minimum.

The convergence speed of the population is related to the convergence speed of all individuals in DE, because the fitness value of the population is the fitness value of the best individual of current iteration. Sometimes the individual with too fast convergence speed leads the entire population to a local minimum trap that hard to be escaped, because the individuals with low convergence speed would learning those with fast convergence speed. But it shows low convergence speed if there are too many low converged individuals in the population. So we want to enhance the convergence properties of those individuals with low convergence speed by using the LM method.

For each target vector ${\overrightarrow{\mathbf{x}}}_{\mathrm{i}}$ of the $n$th iteration, the fitness function is denoted by ${f(\overrightarrow{\mathbf{x}}}_{i,n})$. The convergence speed of target vector and the population of the $n$th iteration are denoted by $∆e_{i,n}$ and $∆E_n$ respectively:

where $eps$ is a small positive number which ensures that $∆E_n$ is greater than 0. Namely, taken $dE$ as the mean convergence speed of the population, so $dE=\left(\sum _{j=1}^n∆E_j\right)/n$. Taken $∆e_i/dE$ as the evaluation index of the convergence rate of the individual to the population.

With the increase of iteration, the convergence speed of individuals and the population changes to a low value, and during the later period it even stops change and the value is nearly equal to 0. Hence the mean convergence speed of the population will be far greater than the individuals because the mean convergence speed of the population is averaged by the speed of all the steps before, including the much greater ones during the initial period. Then the evaluation index $∆e_i/dE$ is nearly 0. To this end, while it is evaluating the convergence rate of the individual, the mean convergence speed of the population is averaged only of several steps before. Assume the length of the evaluation steps is $m$, then $dE=\left(\sum _{j=n-m+1}^n∆E_j\right)/m$. Define event E: the target individual is second trained by LM method.

The probability of the event $E$ should be large, more close to 1, if the individual didn’t find better fitness value. This moment, the convergence speed of the individual $∆e_i$ is less than or equal to 0, and the mean convergence speed of the population $dE$ is greater than 0, so the evaluation index $∆e_i/dE$ is less than or equal to 0.

The probability of the event $E$ should be small, and close to 0, if the individual did find a better fitness value. This moment, the convergence speed of the individual $∆e_i$ is greater than or equal to 0, and the evaluation index $∆e_i/dE$ is less than or equal to 0 too.

So we developed the following expression to set a $P{c}_i$ value for each individual:

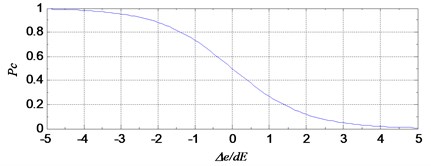
In the process of the algorithm, $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(\right)$ is used to generate a random real number from the interval [0, 1]. If $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(i\right)<{Pc}_i$, make the event $E$ become real, that means the target individual would be second time trained by LM method. Fig. 1 shows the relationship between the probability of event $E$ and the evaluation index of the individual.

Fig. 1The probability of the event E to the evaluation index

3.2. Proposed hybrid training algorithm

The proposed hybrid method combines DE with LM, using the probability adaptive strategy discussed above (DE-LM-PAS). In the process of the algorithm, the target vector is first trained by DE, the new generated target individual is then trained by LM according to the probability which is decided by the convergence speed of the individual and the population. After that, a new trial vector is obtained. The flow of the proposed method is presented:

Step 1: Initialize ${{\mathbf{P}}_G=\{\overrightarrow{\mathbf{x}}}_{i,G}|i=1,2,\dots ,NP\}$.

Step 2: $G=\text{1}$, start the first iteration.

Step 3: $i=\text{1}$, choose the first individual.

Step 4: Take the mutant, crossover and selection operations of the individual ${\overrightarrow{\mathbf{x}}}_{i,G}$, generate the new individual ${\overrightarrow{\mathbf{x}}}_{i,G+1}$ of next generation and update the best individual ${\overrightarrow{\mathbf{x}}}_{best}$.

Step 5: Evaluate the convergence speed $∆e_i$ of each individual and the mean convergence speed $dE$ of the population, then evaluate the probability ${Pc}_i$ of each individual according to Eq. (5).

Step 6: Generate a random number $r_i\in \text{[0, 1]}$. If $r_i>{Pc}_i$, go to step 7, else continue.

Step 6.1: Calculate the Jacobian matrix ${\mathbf{J}(\overrightarrow{\mathbf{x}}}_{i,G+1})$ of the individual ${\overrightarrow{\mathbf{x}}}_{i,G+1}$.

Step 6.2: $∆\overrightarrow{\mathbf{x}}={\left[{\mathbf{J}}^T\mathbf{J}+\mu \mathbf{I}\right]}^{-1}{\mathbf{J}}^T(\mathbf{T}-net({\overrightarrow{\mathbf{x}}}_{i,G+1}\left)\right)$, where $net\left({\overrightarrow{\mathbf{x}}}_{i,G+1}\right)$ is the outputs of the network.

Step 6.3: Get the new trial vector $\overrightarrow{\mathbf{u}}={\overrightarrow{\mathbf{x}}}_{i,G+1}+∆\overrightarrow{\mathbf{x}}$.

Step 6.4: If the fitness value $f\left(\overrightarrow{\mathbf{u}}\right)={f(\overrightarrow{\mathbf{x}}}_{i,G+1})$, then ${\overrightarrow{\mathbf{x}}}_{i,G+1}=\overrightarrow{\mathbf{u}}$ and continue to step 6.4.1, else go to step 6.4.2.

Step 6.4.1: If the fitness value $f\left(\overrightarrow{\mathbf{u}}\right)={f(\overrightarrow{\mathbf{x}}}_{best})$, then ${\overrightarrow{\mathbf{x}}}_{best}={\overrightarrow{\mathbf{x}}}_{i,G+1}$ and go to step 7.

Step 6.4.2: If $\mu <{\mu }_{max}$, then $\mu =\text{10}\mu$ and go to step 6.2.

Step 7: If $i>NP$, go to step 8, else $i=i+\text{1}$ and go to step 4.

Step 8: If a termination condition is reached, exit the loop, and go to step 9, else $G=G+\text{1}$ and go to step 3.

Step 9: Output the network $net\left({\overrightarrow{\mathbf{x}}}_{best}\right)$ with weight vector ${\overrightarrow{\mathbf{x}}}_{best}$.

4.1. Feature extraction

In order to reduce the error rate of classification of the bearing faults, features extracted must reveal enough information of the different types of faults. Hence, only some time-domain features are not enough, frequency-domain features that can reveal more fault information are needed [32]. In this paper, six time domain feature parameters and five frequency domain feature parameters are used for classification of the bearing faults. The difference of the feature values of the data is large, and the normalized treatment is carried out before using the data:

where $x_i$ is the extrated feature value and $y_i$ is the normalized feature value, $x_{max}$ and $x_{min}$ are the maximal and minimal feature values. From the table above, we know that data set C contains 600 samples, half of which are training samples and the rest are testing samples. Here, the 300 training samples of ten classes are used to extracted features. Here the samples are labled with number 1 to 600.

Fig. 3 shows the six time domain features ($T_1$-$T_6$). Most of the features show concentrated in class 1 to class 4, because the defect diameters of the samples of these classes are small, the amplitude and energy of the vibration signal are more steady. The features of class 7 to class 9 are more dispersed, and that makes it hard to identify the fault of same group correctly.

Single feature parameter can be used to identify the different class of samples, because it shows different values between different classes. The feature parameter $T_6$ are obviously different among class 1 to 3, but it almost shows the same value between class 1 and class 4, so the feature parameter $T_2$ can be used to distinguish the two class. Similarly, the feature parameter $T_4$ can be used to distinguish class 5 and class 6, $T_1$ can be used to distinguish class 6 and class 7, $T_3$ can be used to distinguish class 7 and class 8, and $T_2$ for class 8, class 9 and class 10. But while identifying class 7, class 8 and class 9, it is hard to get a high correct rate because of the dispersed feature values. And it is also difficult to identify the ten classes of samples with a high rate at the same time. So much more feature information needed.

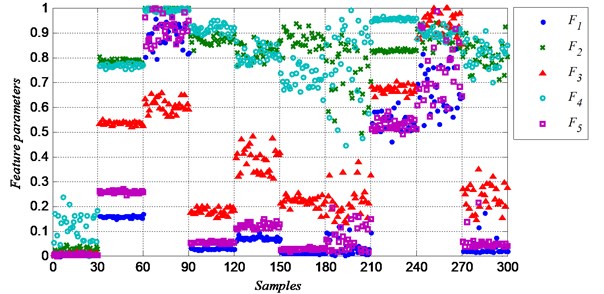
Fig. 4 shows the five frequency domain features ($F_1$-$F_5$). Obviously, the frequency domain features show more difference between groups, and less difference in a group than the time domain features. In class 8, all the time domain features show very dispersed, but the frequency feature $F_2$ and $F_4$ show very concentrated. By using the frequency domain feature, it would highly increase the classification correct rate. Both the time domain and the frequency domain feature values are more dispersed in a group when the defect diameter is bigger, especially in class 7 (ball fault with defect size of D2), class 9 (outer race fault with defect size of D3) and class 10 (ball fault with defect size of D3). Because the uncertainty increase while the fault is becoming worse. That makes it more difficult to classify the different conditions.

Fig. 3Normalized time domain feature parameters

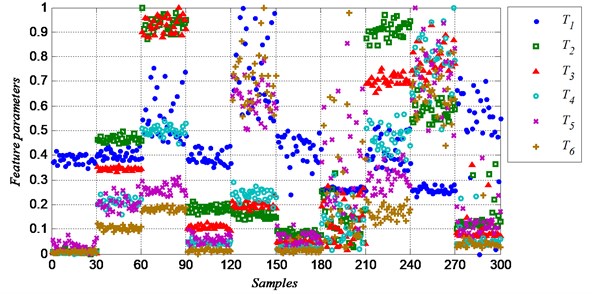
Fig. 4Normalized frequency domain feature parameters

4.2. Faults diagnosis

The multi-layer network classifiers are consists of three layers, the hidden layer contains 15 units, the input layer contains 11 units corresponding to the feature parameters, and the output layer contains units corresponding to the number of classes. The $i$th output of the network is 1, and the rest output is 0 if the sample was labeled $i$.

The single training methods contain gradient decent method (GD), scaled gradient method (SCG), Levenberg-Marquardt method (LM) and differential method (DE). The hybrid training methods contain the hybrid method of DE and LM with a simple strategy (DE-LM) and the hybrid method of DE and LM with a probability adaptive strategy (DE-LM-PAS). First, train the classifiers with the train sets, and then use these classifiers to identify the samples of train sets and test sets. The experiments repeat 10 times, and it stops when the number of net simulation reaches 10⁴ or it meets other termination. The results show in Table 3.

For data set A, it was not very difficult to solve a four class classification problem, classifiers with all train methods got a high correct rate on train set and test set, and all got a rate of 100 % except DE.

For data B, it was more difficult to solve a seven class classification problem. Only two methods got full correct rate of recognition in train set, and all methods performed worse in test set. In all methods, LM, DE-LM and DE-LM-PAS performed better with a high correct rate that is greater than 99 % in either train set or test set.

For data set C, it is very difficult to solve a ten class classification problem. GD, SCG and DE performed much worse than the rest three methods. And among worse methods, SCG was better than the other two methods. From the classification errors shown in Fig. 5, we can see that, the samples which were misclassified were almost from the groups of ball faults with defect sizes of D2 and D3. And the rest three better methods also performed on these samples of ball faults with defect sizes of D2 and D3. On the other fault samples, there were almost no errors as shown in Fig. 6.

Fig. 5Classification errors of GD, SCG and DE

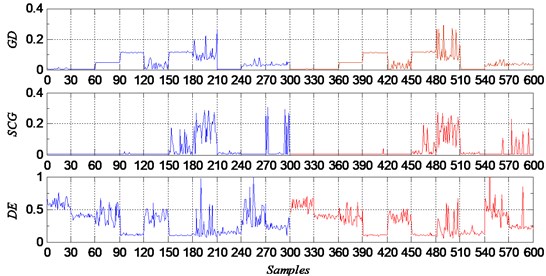
Fig. 6Classification errors of LM, DE-LM and DE-LM-PAS

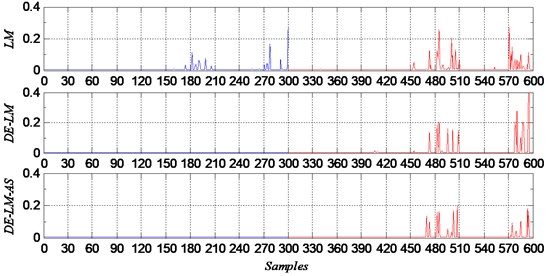
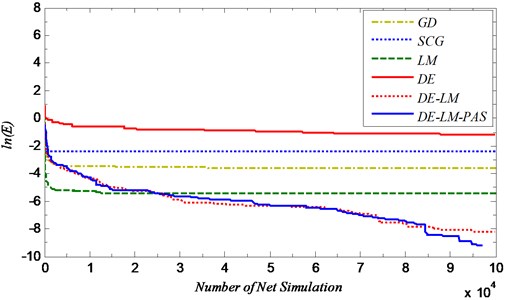
Fig. 7 shows the convergence curves of all methods. The three tradition methods GD, SCG and LM got a fast convergence rate during the initial period, but they stop to obtain a better value after 10⁴th net simulations. However, DE and the hybrid methods could continue to converge during the whole process, but DE finally got a worse result because its convergence speed was slow.

Fig. 7Convergence curves of all method

4.3. Further experiments

In a realistic industrial environment, there is more noise in the signals. So more experiments are request to test how the proposed system operates when signals are embedded into the additive noise. In the experiments below, 20 % noise is added to the signals. Six time domain feature parameters and five frequency domain feature parameters are used, Fig. 8 shows the features extracted.

Fig. 8Features of the signals with 20 % noise

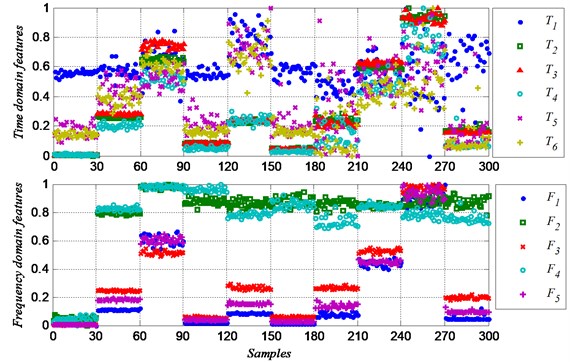
Fig. 8 shows that the time domain feature were infected badly with additive noise, but the frequency feature didn’t show much more different compared with the original signals. The classifiers are also trained by GD, SCG, LM, DE, DE-LM and DE-LM-PAS. The number of hidden layer units and the running options of each algorithm are same as the experiments before. The results show in Table 4.

Compared to the results in Table 3, the results are robust. The noise added into the signals did infect the correct rate of classification, but the infection is limited.

In a realistic industrial environment, the defect size is not just 0.18 mm, 0.36 mm or 0.54 mm, it could be any defect size. It is impossible to identify the uncertain defect size by using any classifiers. But the defect sizes could be clustered into several certain sizes like 0.18 mm, 0.36 mm, etc. If the signals exist difference between feature values, then the proposed system works, and the different faults could be recognized. Furthermore, the experiments above are all the early fault experiments, the defect sizes are relatively close. If differences exist in the feature values of the signals from the experiment, the differences also exist in a realistic industrial environment.