Bifurcations and chaos of rolling bearing system with fault in outer ring

1. Introduction

Bearing is one of the most important part of the rotating machinery and plays a key role for the safe running of equipment. The dynamic characteristics of high-speed rotor system supported by bearings depend largely on bearing properties. Once bearing is broken, it will cause more serious consequences [1-4]. The nonlinear vibration behaviors caused by fault are very complicated, which has significant effect on the design and fault diagnosis of bearing. In order to ensure stable and safe running of rotor system and decrease economic losses and casualties caused by sudden fault in bearings, the nonlinear vibration mechanism and characteristic of bearings with fault need in-depth study.

The present study of dynamical behavior for bearing is mainly concentrated on normal bearing systems. He et al. [5] studied the dynamics of rolling bearing system with gaps under variable load. Zhang et al. [6] investigated the nonlinear dynamic characteristics and stability of rolling bearing system under the influence of non-equilibrium force. Tang et al. [7] obtained the nonlinear bearing force in work situation based on Hertz elastic contact theory and the kinesiology of rolling bearing, and analyzed vibration features of rolling bearing system. Gao et al. [8] established the dynamical equations of the spindle system based on Hertz contact force model and studied mechanism and pathway of the instability. Though these researches acquire some achievements, the appearance of fault is not considered in bearing systems. When a fault occurs in the actual bearing, the interaction between rolling body and inner or outer ring is similar to elastic collision with gaps. Thus the system becomes a non-smooth piecewise linear system. Because the gaps between rolling body and inner or outer ring is very small and this easily results in the instable phenomena of the system, the nonlinear dynamical behavior at the switching plane in bearing systems must be considered to study the mechanism of vibration.

In this paper, the bifurcations and chaos of rolling bearing system with fault in outer ring is studied. The paper is organized as follows. In Section 2, piecewise non-smooth model of rolling bearing system with fault is established by the method of the nonlinear theory. In Section 3.1, the switching matrixes of system are obtained at the switching boundaries to analyze the bifurcation conditions of systems. In Section 3.2 and 3.3, the period-doubling bifurcation and the Neimark-Sacker bifurcation of systems are investigated through the numerical simulations based on theoretical analysis in the Section 3.1. The paper is completed by the conclusions in Section 4.

2. The model of rolling bearing with fault and its motion equation

According to the rolling bearing model with fault in Fig. 1(a), a simplified model of bearing with the fault in outer ring under the condition of single roller is established (see Fig. 1(b)). In the Fig. 1(b), masses $M_1$, $M_2$ and $M_3$ respectively stand for the equivalent mass of inner ring and shaft, the mass of rolling body and the mass of outer ring. Masses $M_1$, $M_2$ and $M_3$ are connected by linear springs with stiffness $K_1$, $K_2$ and $K_3$, and linear viscous dampers $C_1$, $C_2$ and $C_3$, respectively. When fault occurs in outer ring, the spring with stiffness $K_4$ stands for contact state. $F_1\mathrm{s}\mathrm{i}\mathrm{n}\left({\mathrm{\Omega }}_{1}T\right)$ and $F_2\mathrm{s}\mathrm{i}\mathrm{n}\left({\mathrm{\Omega }}_{2}T\right)$ are the equivalent force. ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are the frequency of rotating shaft and cage respectively. $D$ is the fault depth.

Fig. 1The simplified rolling bearing model

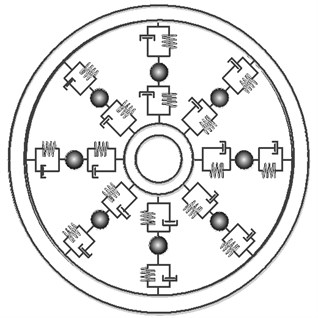
a) Bearing model with fault

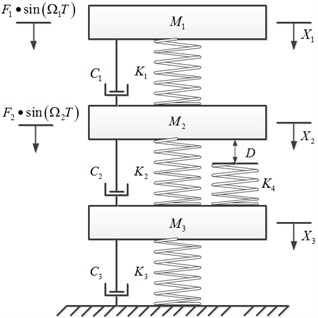
b) The piecewise linear model of bearing with single rolling element

Fig. 2The subspaces of the bearing system

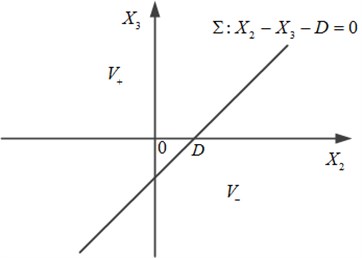
In order to describe the motion process of the bearing system, a switching boundary need be introduced. The boundary function is defined $E=X_2-X_3-D$, and then the switching boundary can be expressed as follows:

Thus the state space is divided into two subspaces by the switching boundary $\mathrm{\Sigma }$, just as shown in Fig. 2.

In Fig. 2, $V_{+}=\left\{X\in R^2\left|E\left(X_2,X_3\right)>0\right.\right\}$ stands for contact state of mass $M_2$ and broken spring $K_4$, $V_{-}=\left\{X\in R^2\left|E\left(X_2,X_3\right)<0\right.\right\}$ stands for separation state.

According to the above analysis, the dynamical equation is established as follows:

in which,

where the dots “$\bullet$” and “$\bullet \bullet$” in the Eqs. (1) and (2) denote the first and second order differentiations with respect to the time $T$, respectively.

Introduce the following non-dimensional quantities:

With the non-dimensional Eq. (3), the original Eq. (1) and (2) can be transformed into the following non-dimensional forms:

in which:

In Eq. (5):

3. Bifurcations of periodic motion in rolling bearing system with fault

3.2. Neimark-Sacker bifurcation

In order to further reveal the bifurcation phenomena of rolling bearing system Eqs. (4) and (5) through numerical simulation, a Poincaré section is chosen as follows:

$\sigma =\left\{\left(x_1,{\dot{x}}_1,x_2,{\dot{x}}_2,x_3,{\dot{x}}_3,\theta \right)\in R^6\times S,\mathrm{}\mathrm{}\mathrm{}\mathrm{}{x}_2-x_3=d,\mathrm{}\mathrm{}\mathrm{}\mathrm{}{\dot{x}}_2-{\dot{x}}_3>0\right\},$

where $\theta ={\omega }_{1}t$.

A set of non-dimensional parameters of the system are chosen as: $d=\mathrm{}$0.0001, $f_1=$ 15, $f_2=$0, $m_2=\mathrm{}$1, $m_3=$ 2, ${\zeta }_1=\mathrm{}$0.1, ${\zeta }_2=\mathrm{}$0.2, ${\zeta }_3=\mathrm{}$0.02, $k_2=\mathrm{}$2, $k_3=\mathrm{}$2, $k_4=\mathrm{}$5.5 and the rotation frequency ${\omega }_1$ is taken as the bifurcation parameter. According to the theoretical analysis in the Section 3.1, we find the bifurcation point ${\omega }_1={\omega }_s=\mathrm{}$2.7724 and compute the corresponding Floquet multipliers as follows:

18

${\lambda }_{\mathrm{1,2}}\left({\omega }_s\right)=-0.6967574\pm 0.3383669\left(\left|{\lambda }_{\mathrm{1,2}}\left({\omega }_s\right)\right|=0.7745729<1\right),$
${\lambda }_{\mathrm{3,4}}\left({\omega }_{\mathrm{s}}\right)=0.4164156\pm 0.9091701i\left(\left|{\lambda }_{\mathrm{3,4}}\left({\omega }_{\mathrm{s}}\right)\right|=0.999996\approx 1\right),$
${\lambda }_{\mathrm{5,6}}\left({\omega }_{\mathrm{s}}\right)=0.3411906\pm 0.2208194i\left(\left|{\lambda }_{\mathrm{5,6}}\left({\omega }_{\mathrm{s}}\right)\right|=0.4064138<1\right).$

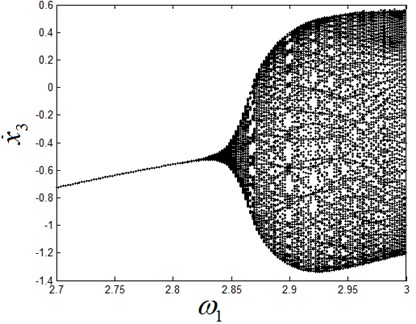
From the characteristic multipliers of Eq. (18), there is a pair of complex conjugated Floquet multiplier is close to the unit circle, i.e. $\left|{\lambda }_{\mathrm{3,4}}\left({\omega }_{\mathrm{s}}\right)\right|=\mathrm{}$0.999996$\approx$1, and the rest of the multipliers are in the unit circle. This shows that Neimark-Sacker bifurcation occurs in the system. The bifurcation diagram with varies of ${\omega }_1$ is shown in Fig. 3.

From the Fig. 3, it can be seen that the stable period-1 motion of system exists in the initial interval of ${\omega }_1$ (see Fig. 4). As the parameter ${\omega }_1$ passes through the bifurcation point ${\omega }_s=\mathrm{}$2.7724, Neimark-Sacker bifurcation takes place. With the further increase of ${\omega }_1$, the period-1 motion loses its stability and bifurcates to a quasi-periodic motion (see Fig. 5).

Fig. 3Neimark-Sacker bifurcation diagram of the system

3.3. Period-doubling bifurcation

In this section, another set of parameters are taken as: $d=\mathrm{}$0.0001, $f_1=\text{20}$, $f_2=\text{0}$, $m_2=\text{1}$, $m_3=\text{2}$, ${\zeta }_1=\text{0.1}$, ${\zeta }_2=\text{0.2}$, ${\zeta }_3=\text{0.05}$, $k_2=\text{1}$, $k_3=\text{20}$, $k_4=\text{16}$, the parameter ${\omega }_1$ is still taken as the bifurcation parameter. The critical bifurcation point ${\omega }_1={\omega }_s=\mathrm{}$8.499 can be found on the basis of analysis of Section 3.1 and the corresponding Floquet multipliers of the system at ${\omega }_s=\mathrm{}$8.499 are computed as follows:

19

${\lambda }_1\left({\omega }_s\right)=-0.999959\approx -1$
${\lambda }_2\left({\omega }_s\right)=-0.6571747(\left|{\lambda }_2\left({\omega }_s\right)\right|=0.6571747<1)$
${\lambda }_{\mathrm{3,4}}\left({\omega }_{\mathrm{s}}\right)=0.7592744\pm 0.5789091i\left(\left|{\lambda }_{\mathrm{3,4}}\left({\omega }_{\mathrm{s}}\right)\right|=0.9547949<1\right),$
${\lambda }_{\mathrm{5,6}}\left({\omega }_{\mathrm{s}}\right)=0.0560869\pm 0.8746048i\left(\left|{\lambda }_{\mathrm{5,6}}\left({\omega }_{\mathrm{s}}\right)\right|=0.8764014<1\right).$

Fig. 4The stable period-1 motion at ω1= 2.75

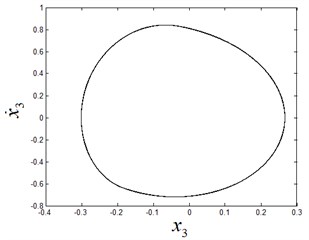
a) The phase diagram

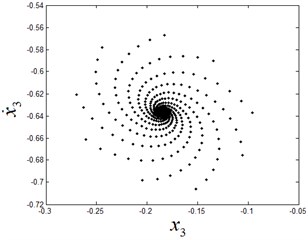
b) The stable focus on Poincaré section

Fig. 5The quasi-periodic motion at ω1= 2.9

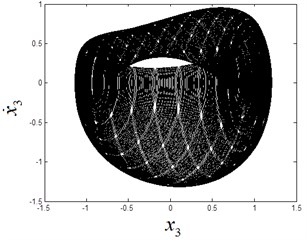
a) The phase diagram

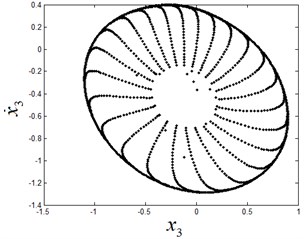
b) The attracting invariant circle on Poincaré section

In Eq. (19), ${\lambda }_1\left({\omega }_s\right)=\mathrm{}$–0.999959 is close to –1, the other Floquet multipliers are still in the unit circle. Thus the period doubling bifurcation occurs in the bearing fault system. Fig. 6 shows a bifurcation diagram for the system.

Fig. 6Period doubling bifurcation diagram of the system

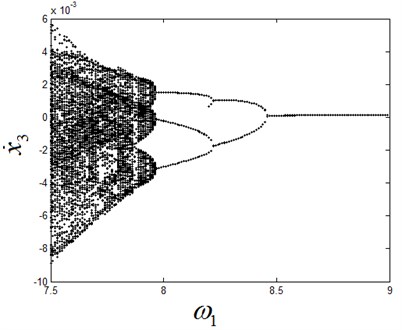
From Fig. 6, the system is in the stable period-1 motion initially. Fig. 7 shows the stable period-1 motion of the system at ${\omega }_1=\mathrm{}$8.55. Period doubling bifurcation occurs when $\omega$ is decreased gradually and passes through the bifurcation point ${\omega }_1=\mathrm{}$8.499, and then the period-2 motion appears, as shown in Fig. 8.

Fig. 7The phase diagram and Poincaré section diagram of period-1 motion at ω1= 8.55

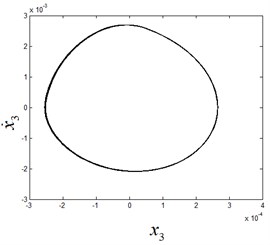
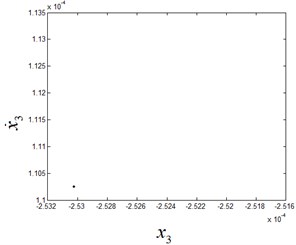
Fig. 8The phase diagram and Poincaré section diagram of period-2 motion at ω1= 8.46

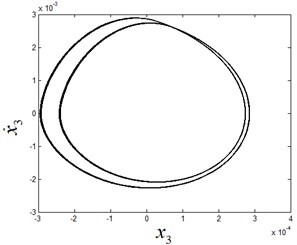
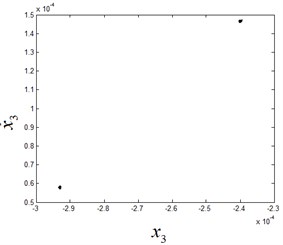
Fig. 9The phase diagram and Poincaré section diagram of period-3 motion at ω1= 8.1

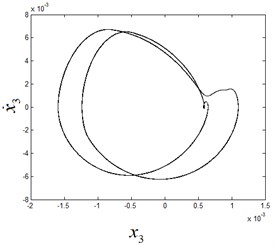
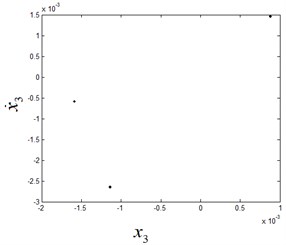
Fig. 10The phase diagram and Poincaré section diagram of quasi-periodic motion at ω1= 7.95

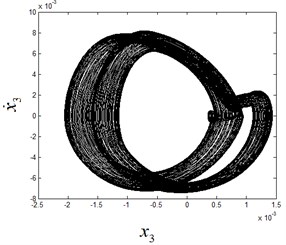
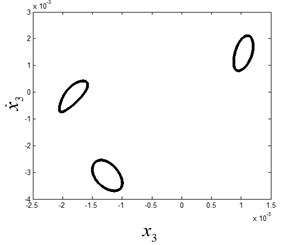
With the decreasing of ${\omega }_1$, the period-3 motion of the system appears, as shown in Fig. 9. When the parameter ${\omega }_1$ is further decreased, the system undergoes Neimark-Sacker bifurcation of period-3 motion and the quasi-periodic motion after bifurcation is shown in Fig. 10. With successive increasing values of the parameter ${\omega }_1$, the system ends up in a chaotic state, as shown in Fig. 11.

Fig. 11The chaotic motion on Poincaré section at ω1= 7.3

4. Conclusions

In this paper we have investigated the bifurcation and chaos of periodic motions of rolling bearing system with outer ring fault. The saltation matrixes at the switching boundaries and the foundation solution matrix in the smooth subspaces are given. Through combining saltation matrixes and foundation solution matrixes, the Neimark-Sacker bifurcation and period-doubling bifurcation of periodic motions of the system are investigated by using Floquet theory. In addition, the phenomenon of Neimark-Sacker bifurcation of periodic three motion and chaotic motion is also revealed in the system. From the results obtained, it is found that the rolling bearing system with fault can exhibit the interesting and complex dynamical behavior. Based on these nonlinear dynamical behaviors of rolling bearing system with fault, the relationship between signal saltation and fault will be revealed from bifurcation perspective by spectral analysis method and Lyapunov exponents method to obtain the set of relevant features of vibration signal in future work. This will provide theoretical basis for fault identification.