Stability and bifurcation of a flexible rod-fastening rotor bearing system with a transverse open crack

2.1. Dynamic modeling of a fastening rod with no crack

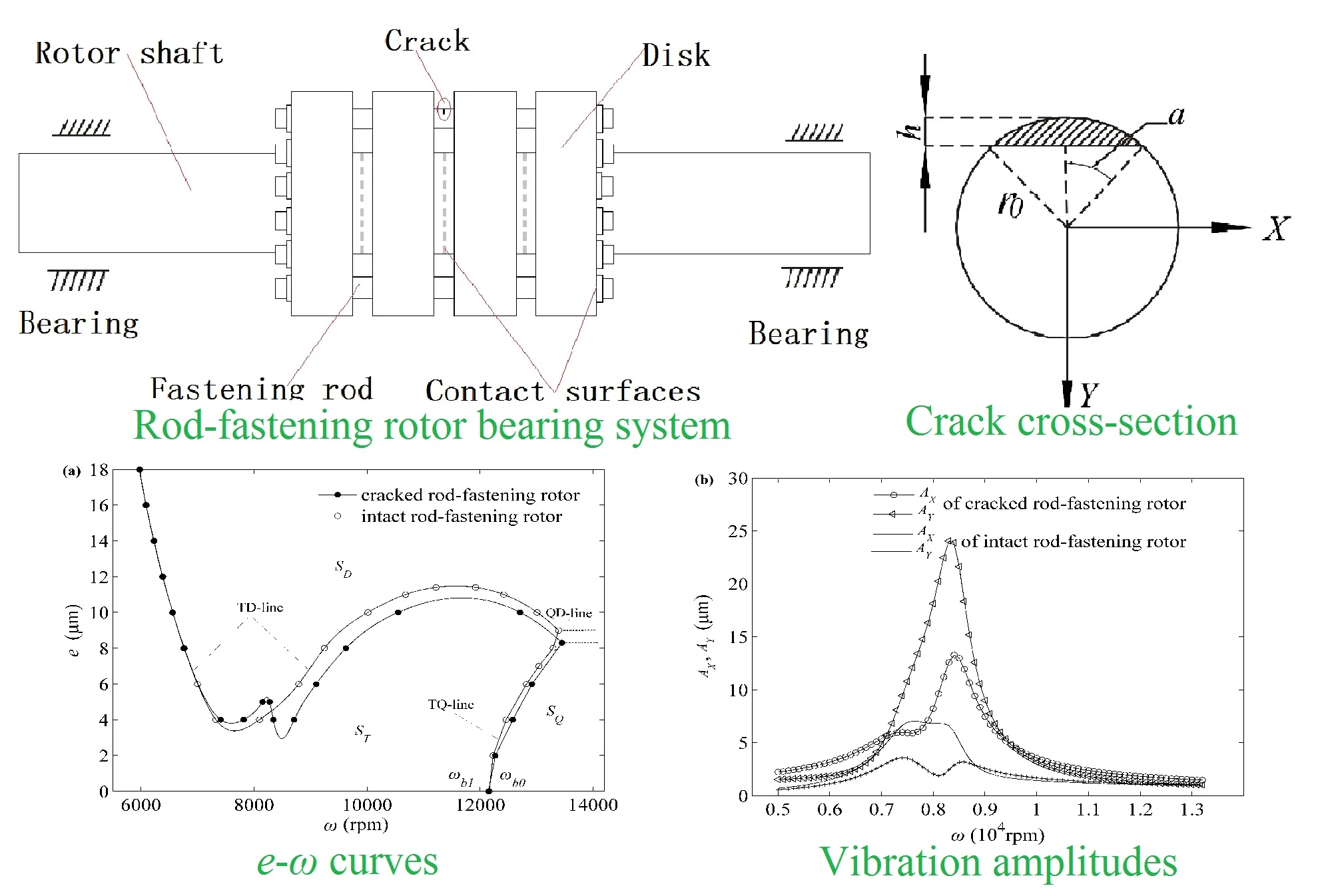
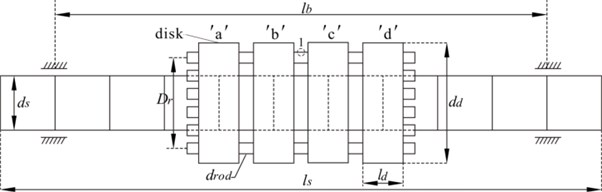
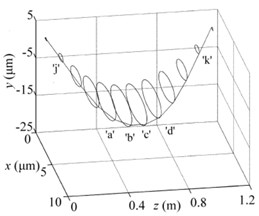
The flexible rod-fastening rotor bearing system is depicted in Fig. 1. Four rigid disks, mounted on the rotor shaft, are fastened by several circumferentially distributed rods and the rotor is supported by two radial cylindrical bearings. The rotor shaft is discretized by using the finite element method with Timoshenko beam, and then the attached fastening rod are modeled as spring element with no mass. The notations as illustrated in Fig. 1 and other essential physical parameters are given in Table 1.

Fig. 1Flexible rod-fastening rotor bearing system. The labels ‘a’, ‘b’, ‘c’, and ‘d’ denote the four disks for distinguishing

The modeling of a fastening rod with no crack as explained in [22, 23] is briefly presented. The instantaneous tension of each rod as shown in Fig. 1 is determined by the position of rod both ending points, which are located on the corresponding disks ‘a’ and ‘d’. According to [22, 23], the elongation and axial force of $i$th fastening rod due to the vibration of rotor system can be expressed approximately as follows:

where ${\phi }_a$, ${\phi }_d$, ${\psi }_a$,$\mathrm{}$and ${\psi }_d$ are the tilting angles. $\omega$ is the rotating speed of the rotor. $r$ is the radius of distributed circumference of the n rods. where ${\gamma }_i$ is the mounted angle of $i$th fastening rod and this rods are distributed averagely with ${\gamma }_i=2\pi i/n$ ($i=$1, 2, …, $n$, $n$ ≥ 3). $F_0^i$, $L$, and $A$ is the pre-tightening force, the original length and the cross-section area of the fastening rod, respectively.

Then the potential energy of $i$th rod is calculated as the following:

Thus, the total potential energy with $n$ fastening rods distributed along the circumference averagely can be given as:

Substituting the Eq. (1) into Eq. (4) and according to the geometrical relationship, the Eq. (4) can be expressed as follows:

with$a=r\sum _{i=1}^n{F}_0^i\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t+{\gamma }_i\right)$, $b=r\sum _{i=1}^n{F}_0^i\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t+{\gamma }_i\right)$, $c=nEA{r}^2/2L$, and the constant stiffness matrix ${\mathbf{K}}_{rod}$ as followed in Eq. (6):

In fact, in Eq. (5), the first term is caused by the generalized moment of the pre-tightening force, the second term is regarded as the dynamic stiffness term. When the pre-tightening forces for per rod is equal ($F_0^i=const$ and $a=b=$ 0), the $n$ rods only provide a constant stiffness matrix ${\mathbf{K}}_{rod}$, and in contrast with an add-on moment vector ${\mathbf{f}}_{rod}$ as shown in Eq. (7) besides stiffness matrix ${\mathbf{K}}_{rod}$:

2.2. Dynamic model of the fastening rod with a transverse open crack

Because per fastening rod is mainly subjected to the axial big tension stress due to the pre-tightening assembling, which far outweighs the compressive stress and additional bending stresses caused by the system gravity. This will determine the open crack state of cracked rod in practical work when there is a crack in a fastening rod. Besides the contact edge position of disk and fastening rods always introduces the phenomenon of stress concentration. When there is a transversal open crack on the surface of a fastening rod in “1” location as depicted in Fig. 1, it always introduces the phenomenon of stress concentration and the reduction of stiffness, and the stability of the whole rotor bearing system will change compared with intact ones (which has no crack on the fastening rod). The schematic of a transversal open crack in a fastening rod is illustrated in Fig. 2.

Fig. 2The cross-section area of the cracked fastening rod, where h, r0 and α are the depth of crack, the radius of the fastening rod and the semi-central angel corresponding to the half width of a transverse crack, respectively

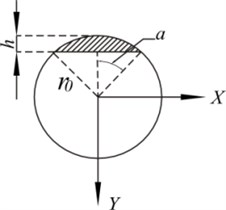
When a transverse open crack occurs on the surface of the $j$th fastening rod, the crack section area and the instantaneous axial force of $j$th rod can be derived respectively as follows:

with $\lambda =h/r_0$.

Substituting the Eq. (8) into the Eq. (9), the instantaneous axial force of the $j$th fastening rod with a crack can be expressed as:

The potential energy of $j$th cracked fastening rod can be given as:

Substituting the Eqs. (1) and (5) into the Eq. (11), the total potential energy of $j$th cracked fastening rod and the others with no crack can be given as:

with:

and the add-on stiffness matrix stiffness matrix ${\mathbf{K}}_{rodc}$ as followed in Eq. (13):

It can be found that Eq. (5) and Eq. (12) are different, which shows the cracked rod-fastening rotor system will introduce the add-on stiffness matrix ${\mathbf{K}}_{rodc}$ as shown in Eq. (13) besides ${\mathbf{K}}_{rod}$ in Eq. (6) compared with intact rod-fastening rotor system.

It is note that the additional stiffness matrix of the cracked fastening rod as shown in Eq. (13) is asymmetric. This asymmetry will break the existed relatively steady state of rotor system resulting in the change of the system stability. Meanwhile, the contribution of the additional stiffness matrix introduced by the crack is to reduce total stiffness of the system.

2.3. Dynamic equations of cracked rotor bearing system

The finite element method with Timoshenko beam element with four degrees of freedoms at each node is employed to discretize the rotor into 11 elements [24-27]. The four disks, fastening rods and two radial cylindrical bearings are assembled together with the rotor through the finite element method. Then the dynamic equation of the cracked rod-fastening rotor bearing system is formulated as follows:

with:

where $\mathbf{M}$, $\mathbf{G}$, $\mathbf{K}$, and $\mathbf{Q}$ are the mass matrix, gyroscope matrix, stiffness matrix and the external force vector (including gravity and unbalance force), respectively, and the corresponding superscript ‘$S$’, ‘$r$’, and ‘$d$’ stand for the whole system, rotor shaft and disk, respectively. $\mathbf{x}$ is one single node displacement vector, which have translational and rotational displacement about $X$-and $Y$-axes of the fixed coordinate system, i. e. $\mathbf{x}={[x,y,\psi ,\phi ]}^T$. So for the displacement vector of a rotor with $n$ nodes, it can be given as ${\mathbf{x}}^{\mathrm{S}}={\left[x_1,y_1,{\psi }_1,{\varphi }_1,\cdot \cdot \cdot ,x_n,y_n,{\psi }_n,{\varphi }_n\right]}^T$. ${\mathbf{K}}_{rod}^S$ is the $4n\times 4n$ (node number $n=$ 12) stiffness matrix which consists of ${\mathbf{K}}_{rod}$. ${\mathbf{K}}_{rodc}^S$ is the $4n\times 4n$ stiffness matrix of which the entries of zero entries except at the crack node location are equal to ${\mathbf{K}}_{rodc}$. ${\mathbf{F}}_{rod}$ and ${\mathbf{F}}_{oil}$ are $4n\times 1$ matrix of which the entries of zero entries except at the corresponding node location are equal to ${\mathbf{f}}_{rod}$ and ${\mathbf{f}}_{oil}$, respectively. The oil force vector can be expressed as ${\mathbf{f}}_{oil}=(f_{bx},\mathrm{}{f}_{bx},\mathrm{}0,\mathrm{}0{)}^T$ , which can be obtained from the typical infinite long bearings assumption [28].

3.1. Method of solutions

The whole system have 48 DOFs which contain linear and nonlinear DOFs. Although it is not very high dimension for advanced computer technology nowadays, it also need consume much time for real time simulation at different speeds. To save the computing time and retain necessary DOFs information, the free interface modal synthesis technology [22, 23 29, 30] are employed to reduce the system DOFs. The nonlinear DOFs corresponding to two bearing nodes and four disks nodes and other two corresponding nodes of linear DOFs are retained. Then the reduced system can be given as follows:

where $\mathbf{M}={\mathbf{T}}^T{\mathbf{M}}^S\mathbf{T}$, $\mathbf{G}={\mathbf{T}}^T{\mathbf{G}}^S\mathbf{T}$, $\mathbf{K}={\mathbf{T}}^T{\mathbf{K}}^S\mathbf{T}$, and $\mathbf{Q}={\mathbf{T}}^T{\mathbf{Q}}^S+{\mathbf{T}}^T{\mathbf{F}}^S$. $\mathbf{q}$ is the reduced displacement vector. $T$ is a transformation matrix being introduced to reduce the original system. By introducing the state variable $\mathbf{X}={\left({\mathbf{q}}^T,\mathrm{}{\dot{\mathbf{q}}}^T\right)}^T$, the corresponding reduced system equations in a state space can be written as follows:

By system reduction, the local nonlinearity of nodes which locates in bearings and disks are retained as well as other two linear nodes, which means 32 DOFs in total are kept. Then the nonlinear stability and bifurcation behaviors can be obtained by numerical simulations.

Assuming that the system is subjected to the external periodic load ${\mathbf{Q}}_{ex}\left(t\right)$ with period $T_0$, i.e. ${\mathbf{Q}}_{ex}\left(t\right)={\mathbf{Q}}_{ex}(t+T_0)$, which originates from the mass eccentricity. Then periodic solutions can be are calculated by solving a two point boundary value problem, which is defined by Eq. (19) supplemented with the boundary condition $\mathbf{X}\left(t\right)=\mathbf{X}(t+T_0)$. It can be written as:

with $\mathbf{f}(\mathbf{X},\mathrm{}t,\mathrm{}\lambda )=\left(\begin{array}{c}\dot{\mathbf{q}}\\ {\mathbf{M}}^{-1}\left(\mathbf{Q}-\mathbf{K}\mathbf{q}-\mathbf{G}\dot{\mathbf{q}}\right)\end{array}\right)$, where $\lambda$ is a system parameter, which can be the angular speed $\omega$ or the mass eccentricity $e$, etc.

The periodic solutions of the system will become unstable in certain intervals of system parameters. It is important to determine the unstable intervals and which kind of nonlinear dynamic behaviors of system among the periodic, quasi-periodic, and chaotic it is. Here, for a given system parameter, the shooting method [22, 23, 29, 31-33] is adopted to obtain the details of periodic solutions. Then the path-following technique [31, 33] is used to investigate how a periodic solution is influenced by a change of $\lambda$. The whole solution braches of system can be found with this combined technique, which is consist of a predictor-corrector mechanism as shown in Eq. (21) in nature:

For the Eq. (21), the next step solution, i.e. ${\mathbf{X}}_{n+1}$ at ${\lambda =\lambda }_{n+1}$, can be determined by starting from a known solution ${\mathbf{X}}_n$ at ${\lambda =\lambda }_n$, and combining with the corrected mechanism by using shooting method.

Lastly, the Floquet theory [22, 33] is employed to determine the local stability of periodic motion of nonlinear system. The procedure involves calculating the largest eigenvalues (Floquet multipliers) of the Jacobian matrix (the details see the [22, 23]) produced in the process of the shooting method. In general, the Floquet multipliers must be within the unit circle in the complex plane. While with the change of the system parameter, the stable periodic solution of system will happen to lose stability, which will show different forms of bifurcation.

According to the situation of the maximum Floquet multipliers through the unit circle in the complex plane, the forms of bifurcation can be classified into three modes i.e. period-doubling bifurcation, quasi-periodic bifurcation and “cycle-fol” or “transcritical” bifurcation [23].

Each finite element node of system as shown in Fig. 1 is marked by integer from 1 to 12 in sequence. The corresponding parameters of the cracked and intact rod-fastening rotor bearing system are given in Table 1. The mass eccentricities of four disks are represented by $e_a$, $e_b$, $e_c$, and $e_d$ ($e_a=e_b=e_c=e_d=e$) which results in the unbalance forces of system. Meanwhile, the numerical results of rod-fastening rotor system model with no crack as referred in [22, 23] are also given for comparison. The simulation results are obtained as shown from Fig. 3-11, respectively, through Fortran program by changing corresponding parameters.

3.2. Simulation results and nonlinear analysis

3.2.1. Effects of crack on the system stability and bifurcation

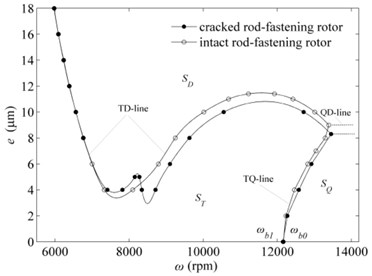
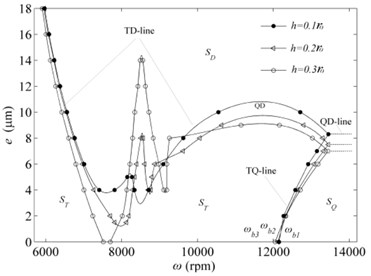
For a given crack depth $h=$ 0.1$r_0$ of the cracked fastening rod, the regulations of the stable and unstable solutions of the system with the change of the system parameters $e$ and $\omega$ for both cracked rod-fastening rotor bearing system and intact ones are shown in Fig. 3(a).

Fig. 3a) e-ω curves of the solution set of stability and bifurcation transition of the cracked and intact rotor systems, b) effects of the crack depth on the system stability and bifurcation

a)

b)

Compared with intact rod-fastening rotor system, in general, the stability and instability regions of the cracked ones also have three parts, the stable $T$ periodic motion region $S_T$, the period-doubling motion region S_D and the quasi-periodic motion region $S_Q$ which are developed by the corresponding two borderlines of TD-line, TQ-line and QD-line, respectively, as shown in Fig. 3(a). The TD-line and TQ-line are the period-doubling bifurcation borderline and quasi-periodic bifurcation borderline, respectively. Periodic-doubling motion or quasi-periodic bifurcation motion will occur when the rotating speed ω or the mass eccentricities $e$ crosses TD-line or TQ-line. The dashed QD-line is the critical parting line of period-doubling bifurcation motion region S_T and quasi-periodic bifurcation motion region S_Q. The symbols $w_{b0}$ and $w_{b1}$ in Fig. 3(a) as well as $w_{b2}$ and $w_{b3}$ mentioned later in text are linear critical speed of the equilibrium point for the balanced rod-fastening rotor system ($e=$ 0) and $w_{b0}$, $w_{b1}$, $w_{b2}$ and $w_{b3}$ correspond to the crack depth equaling to 0, 0.1$r_0$, 0.2$r_0$, and 0.3$r_0$, respectively. Hopf bifurcation will occur for the system and subsequently lose stability when the rotating speed exceeds linear critical speed for the balanced rod-fastening rotor system.

It is worth noting that there are some different details between cracked rod-fastening rotor system with a transverse open crack in a fastening rod and intact ones as follows

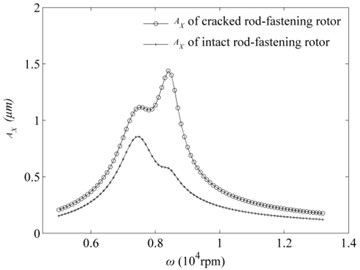
Firstly, the $e$-$w$ curve of cracked rotor system tends to move to the lower right as a whole and the QD-line tends to a downward move. These differences are mainly caused by the existence of crack of the fastening rod which will introduce the additional stiffness and cause system stiffness to reduce. While these changes are very small when the rotating speed is approximately on the left side of the first saddleback of TD-line which corresponds to the location of the first resonance peak in Fig. 4(a) probably. This means the influences of shallow crack of the fastening rod on system dynamic behaviours is small for rod-fastening rotor system when they work under the rotating speeds corresponding to the first resonance peak.

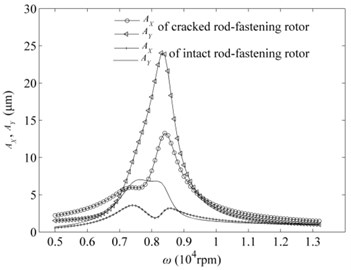
Fig. 4Vibration amplitudes when h= 0.1r0 and e= 1 μm: a) bearing node, b) middle disk node

a)

b)

Secondly, it can be found that it happens to two saddlebacks of TD-line as shown in Fig. 1 which approximately corresponds to the two resonant peaks of bearing node for cracked rod-fastening rotor system as shown in Fig. 4(a). In contrast with the intact rotor system, the TQ-line shows just a saddleback. Thus, they will perform different dynamic behavious and stability in the location of second saddleback of cracked rod-fastening rotor system which one is stable and another is periodic-doubling bifurcation behaviours because of the presence of crack on the surface of the fastening rod. It is also worthwhile to note that the vibration amplitudes of the cracked rod-fastening rotor system under stable region with 1 μm mass eccentricity is bigger compared with the intact rotor system as shown in Fig. 4(a, b), especially for the middle disk node as shown in Fig. 4(b).

Thirdly, the TQ-line shows a linear growth trend with the increment of rotating speeds and the mass eccentricities for two systems. Although the most part of TQ-line seems to move slightly to the right for cracked rotor system, it tends to move slightly to the left when the mass eccentricities equals to zero or near the zero regions. It can be seen that the linear critical speed $w_{b1}$ of cracked rotor system locates on the right of the linear critical speed $w_{b0}$ of intact ones. This shows the cracked rod-fastening rotor system will early to lose stability for balanced ones (mass eccentricities $e=$ 0) or very small mass eccentricities compared with intact rotor system.

3.2.3. Effects of mass eccentricity

In this part, the effects of typical mass eccentricities $e=$ 0 μm, 8.3 μm, and 12 μm on the dynamic behaviours such as orbits of periodic motion, vibration model, frequency spectrums analysis, and Poincare map are studied as well as the intact ones in literature for comparison.

(1) Mass eccentricity $e=$ 0 μm.

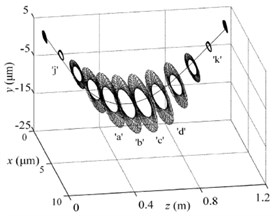
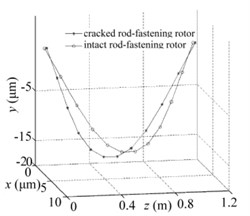
It can be obtained that the cracked rod-fastening rotor system and intact ones lose their stabilities at $w_{b1}$ (12150 rpm) and $w_{b0}$ (12160 rpm), respectively from Fig. 3(a). While the form of transition from steady state to full unstable state is different. After crossing the linear critical speed $w_{b1}$ and $w_{b0}$, for example at 12240 rpm, the cracked rotor system loses stability by quasi-periodic bifurcation as shown in Fig. 5(a) which shows the orbits of whole 12 nodes and the intact ones by Hopf $T$ periodic solution as shown in Fig. 5(b). The vibration modes of rotor shaft of two systems at a transient time is different and it shows the vibration amplitude of cracked rotor system tends to be larger than the intact ones due to the presence of the crack of rod-fastening as depicted in Fig. 5(c).

Fig. 5Periodic solutions for all nodes when e= 0 μm and w= 12240 rpm: a) Quasi-periodic solutions for cracked rod-fastening rotor system with h= 0.1r0, b) Hopf T periodic solutions for intact systems, c) comparison of the whole vibration modes of two systems

a)

b)

c)

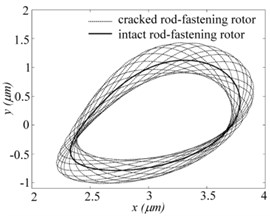
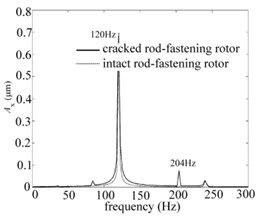
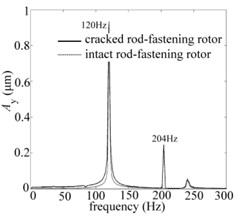
In order to further explore the dynamic behaviours, Fig. 6(a), (b) and (c) shows the orbits and frequency spectrum of bearing node. It can be seen clearly that the quasi-periodic bifurcation behaviours for cracked systems and Hopf $T$ periodic bifurcation for intact ones in Fig. 6(a). Besides there are some differences in frequency component, which occurs to whirling frequency about 204 Hz for cracked system except the whirling frequency about 120 Hz compared with the intact ones as shown in Fig. 6(b, c).

(2) Mass eccentricity $e=$ 8.3 μm.

According to the Fig. 3(a), it can be known that the cracked rod-fastening rotor system occurs to lose stability at $w=$ 13450 rpm when mass eccentricity $e=$ 8.3 μm as well as at $w=$ 13370 rpm for intact ones. Fig. 7(a) shows the periodic-doubling motion at $w=$ 13458 rpm and periodic-doubling motion at $w=$ 13440 rpm of bearing node for two systems respectively when $e=$ 8.3 μm. Poincare maps is a closed curve consisted of limited points for cracked system and the others are two isolated points for intact ones in Fig. 7(b), which confirms the corresponding motions are periodic-doubling and periodic-doubling, respectively. The frequency spectrums of $Y$ direction are illustrated in Fig. 7(c) which shows the frequency components are very consistent. This means that it is difficult to distinguish the cracked and intact rod-fastening rotor bearing systems by frequency components on this condition.

Fig. 6The bearing node dynamic behaviours when e= 0 μm and w= 12240 rpm for two systems: a) orbits, b) and c) frequency spectrums of X and Y direction, respectively

a)

b)

c)

Fig. 7Periodic-doubling (w= 13458 rpm) and quasi-periodic (w= 13440 rpm) solution of bearing nodes for two systems respectively when e= 8.3 μm: a) orbits, b) Poincare map, c) frequency spectrums

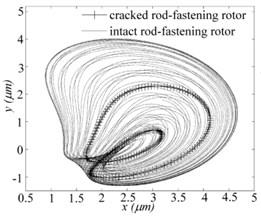
a)

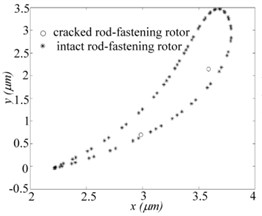
b)

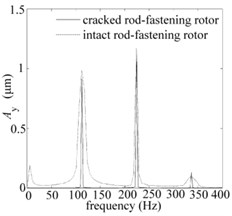
c)

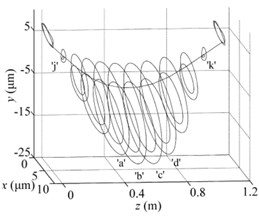
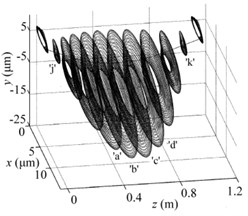
Fig. 8Solutions for all nodes when e= 8.3 μm: a) periodic-doubling solution (w= 13458 rpm) for cracked rod-fastening rotor system, b) quasi-periodic solution (w= 13440 rpm) for intact ones, c) comparison of the whole vibration modes for two systems

a)

b)

c)

Fig. 8(a, b) shows the periodic-doubling motion and quasi-periodic motion of the whole nodes for cracked and intact rod-fastening rotor system, respectively. Fig. 8(c) gives the vibration modes of two systems. Because of the presence of crack for cracked system, the vibration amplitude of cracked system is larger than the intact ones.

(3) Mass eccentricity $e=$ 12 μm.

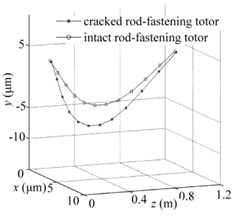
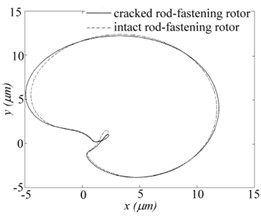
The nonlinear dynamic behaviours for two systems are very consistent when the crack depth is 0.1$r_0$ and the system work on the left side of the first saddleback according to $e$-$w$ diagram in Fig. 3(a). It can be seen that the periodic motions of bearing nodes occur for cracked and intact rotor system as shown in Fig. 9(a), and the two isolated points of Poincare maps as shown in Fig. 9(b) also confirm this nonlinear dynamic behaviours. Besides the frequency components of bearing node of frequency spectrums of $X$ direction in Fig. 9(c) are also same. In addition, the solutions of whole nodes are very consistent and periodic motions as shown in Fig. 10(a) and (b) as well as the vibration modes in Fig. 10(c). This reveals that the effects of crack are very small to some extent, especially when the system works under in the range of the first resonance peak and has a slight crack depth. While this phenomenon will change with the increment of crack depth as shown in Fig. 3(b).

Fig. 9Periodic-doubling solution (w= 6400 rpm) of bearing nodes for two systems respectively when e= 12 μm: a) orbits, b) Poincare map, c) frequency spectrums of X direction

a)

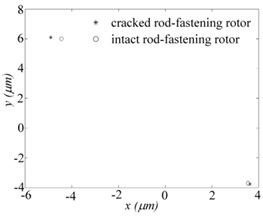
b)

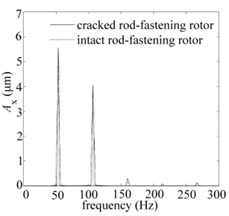
c)

Fig. 10Periodic-doubling solutions for all nodes when e= 12 μm and w= 6400 rpm: a) cracked rod-fastening rotor system, b) intact rotor system, c) the whole vibration modes for two systems

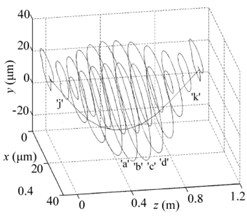
a)

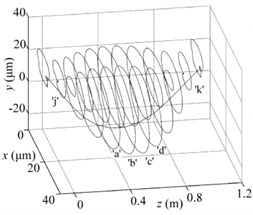
b)

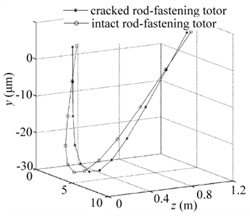
c)