Optimum design of printed electronics inkjet printer using response surface model and multi-objective genetic algorithm

2.1. FEA of the inkjet printer

Considering the relative movement between parts and different materials they are made of, the model mainly contains six parts: base, bed, a workbench, lateral guide rail and leadscrew, a longitudinal guide rail and leadscrew, and an inkjet head unit. The bed comprises of table, column and top beam. While the base is made of SPCC and bed of granite, the inkjet head unit and workbench are of Unifont90, and the guide rail and leadscrew are of GCr15. Fig. 1 is the CAD model of a certain type of inkjet printer.

Fig. 1CAD model of the inkjet printer: 1 – Workbench; 2 – Longitudinal guide rail and leadscrew; 3 – Inkjet head unit; 4 – Lateral guide rail and leadscrew; 5 – Bed; 6 – Base

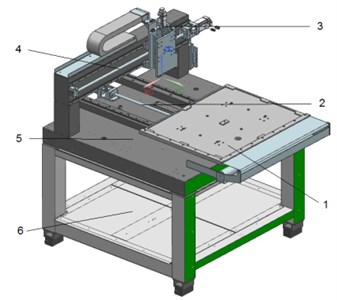
Fig. 2FEM of the inkjet printer

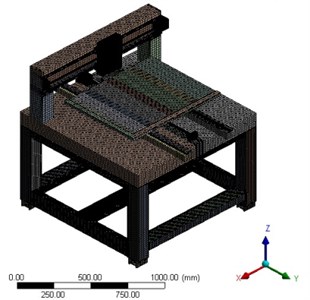
To avoid finite element mesh distortion brought by some detailed structure features such as chamfer, auxiliary hole and to further improve the mesh partition quality, the FEM of inkjet printer has to simplify or remove some parts or detailed features which have no or little impact on the analysis [10]. The inkjet printer is mesh partitioned into hexahedral solid 186 unit grid to improve the accuracy and reduce calculation scale. The FEM, as shown in Fig. 2, utilizes slice, edge sizing, body sizing and hex dominant, etc. to control the shape and size of grid. The type of contact between the parts and component is defined as Non Separation.

Although the above FEM strives to reflect the real inkjet printer structure, it cannot guarantee its accuracy and reliability due to the simplification of model, idealization of material, and simulation of combining surfaces in the process of model establishment. So this study will combine the FEA with EMA to modify and verify the FEM through the analysis of the natural frequency and vibration of the inkjet printer. Hence it ensures that the established FEM is valid for further analysis and optimization.

Since the inkjet printer is supported by four iron pads attached to the bottom surface, there is no relative sliding between the inkjet printer and ground and the friction is idealized as infinite. So the four bottom supports are constraint as fixed, and their six degrees of freedom are defined. Due to the excitation frequency of the motor is about 50 Hz, frequency range to be analyzed is 0-200 Hz. The first five order natural frequency values and the corresponding vibration modes are shown in Table 1.

2.2. EMA

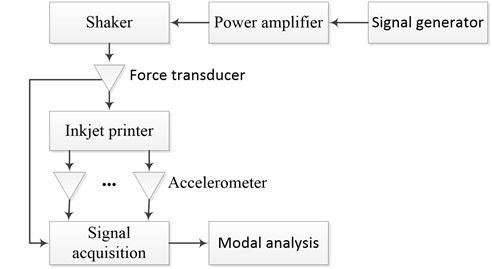
By giving excitation to fixed points and then collecting response signals, we carried out an EMA to verify the accuracy of the FEM. The measurement system is shown in Fig. 3. Apart from the inkjet printer, it consists of three main parts: exciting system, response signal collecting system and modal analyzing and processing system. Exciting system includes the signal generator, the power amplifier and the shaker while the accelerometer, force transducer and signal acquisition are responsible for collecting response signals. LMS Test.lab is used for modal analysis and process.

Fig. 3Block diagram of the testing system

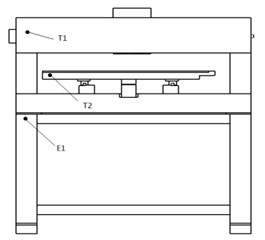
The inkjet printer was placed in its normal operating position in the modal test. The measuring points and exciting points were arranged mainly on parts of comparatively bigger deformation based on the FEA results. Single point excitation method was used to vibrate the whole machine. The excitation signal was sinusoidal, and the frequency range was 0-200 Hz. The location of exciting points should fully motivate system vibration and the motivation direction should conform to that of the vibration. The location of measuring points should reflect as accurately as possible the vibration position of the mode. In this study, the measuring and vibrating point distribution is as shown in Fig. 4 with E1 and E2 as the exciting points, T1, T2, T3 and T4 as the measuring points. The frequency response curves are shown in Fig. 5.

Fig. 4Exciting points (E1, E2) and measuring points (T1, T2, T3, T4) distribution from

a) Front

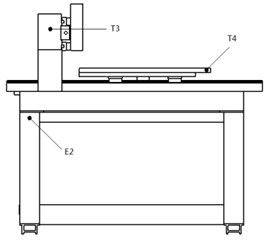
b) Flank

Fig. 5FRF experimental results of measuring points

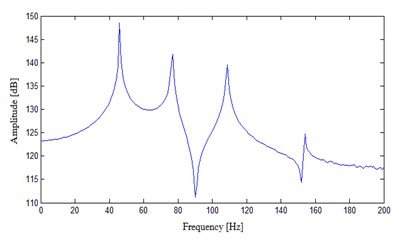
a) T1

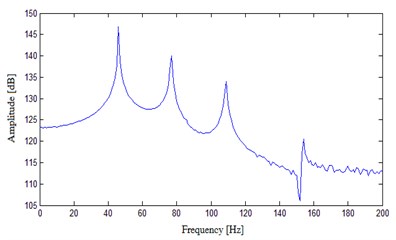
b) T2

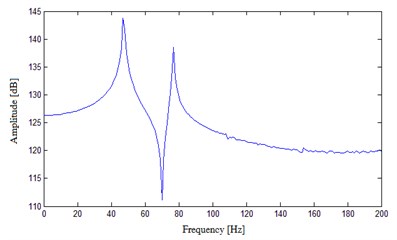
c) T3

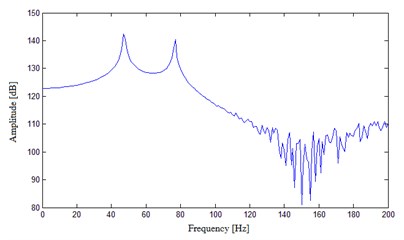
d) T4

The results show that the EMA can well stimulate the natural frequency of the system structure. The comparison of experimental results and those of FEA, as shown in Table 1, indicates the relative errors are less than 5 %. The high consistency has proved the reliability of the FEM and the analysis results.

2.3. Static and dynamic characteristic analysis

The printing performance is mainly decided by the inkjet printer’s mechanical structure and control system. The performance of the latter is also realized through the system’s mechanical structure. Therefore, the properties of mechanical structure decide directly the working performance of the inkjet printer [11, 12]. The static characteristics of the inkjet printer are reflected in the structural deformation caused by global gravity and driving forces while its dynamic characteristics are mainly manifested in the motor vibration.

2.3.1. Static characteristic analysis

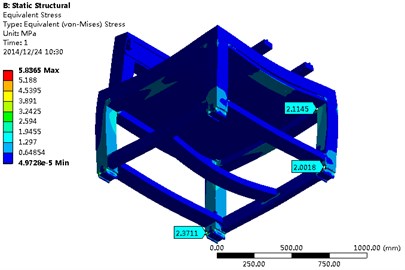
Apart from the fixed constraint, standard earth gravity was imposed to the inkjet printer. The deformation of the whole structure and the stress response were set to be output, as shown in Fig. 6 and Fig. 7.

Fig. 6Nephogram of inkjet printer deformation

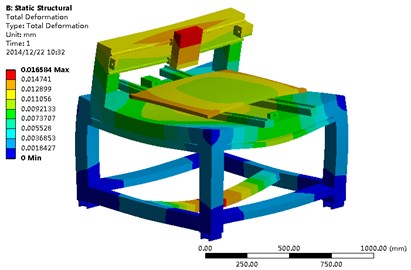
Fig. 7Nephogram of inkjet printer stress

From Fig. 6, the maximum deformation is 0.016584 mm. The twisting deformation appears in the upper part of inkjet head module around the $X$ axis while the workbench presents downward deflection in its center along the $z$-axis. Deformations of other parts are secured within 0.015 mm. So the whole structure satisfies the design requirements. The figure displays relatively big deformation in the base due to the gravity of the machine. So the thickness of the columns and beams in the base and the beam lengths along $Y$ direction should be adopted as design variables to improve the stiffness of the inkjet printer.

As shown in Fig. 7, the inkjet printer generally takes on blue, which means the overall stress is below 0.64854 MPa. The base is under relatively greater stress, with the maximum of 5.8365 MPa. It can be explained by the fact that the base is made of hollow material, but bears the weight of the whole machine. So it is the weak stress region. It can be strengthened through enhancing the thickness of the base columns and beams. While the maximum stress of the whole inkjet printer is far below the allowable stress of SPCC material, the inkjet printer structure excepting the base part has great possibility to be optimized from the perspective of the machine’s overall strength.

3.1. CCD

In order to construct the response surface model, this study adopted the CCD, a method evolved from second order whole plot factor and subplot designs. The nonlinear relationship between the evaluation index (output variable) and the factors can be evaluated by increasing a design point (equivalent to an increase of a level) in the second order experiment. In addition, CCD can be applied to different design and operation domains [17]. Therefore, the method has the virtue of reflecting the characteristics of the whole design space with fewer sample points. It is of high design efficiency and wide adaptability. For the experiment of second order $n$ factor, the test points include the following three parts: 1 central point, $2n$ axial points and $2^{n-\xi }$ analysis points. The total testing points needed $P$ can be calculated through the following formula:

where $n$ is the number of design variables, $\xi$ is the factorial coefficient.

3.2. Response surface model

This study chose the second order polynomial response surface model with higher accuracy. The model with $n$ design variables can be expressed as [18]:

where $y$ indicates the output variable, $x_i$ is the design variable, $n$ represents the number of design variables, $\beta$ is the unknown coefficient vector, which can be obtained by the least square regression method.

3.3. Evaluation of response surface model

The perfection degree of the approximate function model established, i.e. the response surface model, directly affects the optimization results. Therefore, it should be evaluated. Goodness of fit is usually used to measure the fitting degree of the response surface model to the experimental data [19]. The negative correlation coefficient $R^2$ varying within [0, 1] is the index to measure the correlation degree. The closer it is to 1, the less error it indicates, hence, the higher the response surface accuracy:

where $E$ is the square sum of the response value and the estimated response value while $Y$ is the square sum of the difference between the response value and the average response value.

3.4. MOGA

In the process of actual engineering optimization, it often involves multiple parameters. This is the multi-objective optimization. These objectives are often inter-connected and restricted. The promotion of one target performance often leads to the decrease of other target performance. So there usually does not exist a singly optimal solution to realize all optimal indexes. Instead only a set of multiple optimal solutions can be reached, known as Pareto optimal solution set. The superiority of these optimal solutions cannot be compared with each other. The selection may require trade-offs and comprises among the criteria being considered [20]. MOGA takes optimal solutions in the feasible region as individuals in a population, and encodes them as chromosomal strings for selection, crossover and mutation. Through the population ranking and crowding distance calculation, on the basis of fitness, the individuals evolve from generation to generation to gradually approach the optimal solution [21]. MOGA provides an effective direct search method. It has been widely used since the global optimal method it furnished has strong applicability to solve big and complex optimization problems.

In the optimization of inkjet printer, weight reduction and promotion of the structure dynamic and static characteristics are inter-restricting. So it belongs to multi-objective optimization design problem. The optimization target is to reduce the inkjet printer weight as far as possible under the condition that mechanical structure of overall inkjet printer meets the requirements of both static and dynamic characteristics and the work performance. The MOGA is used to optimize the structure design of inkjet printer in this study.

5.1. Problem description

The analysis of both the static and dynamic characteristics of the inkjet printer shows: a) under working condition, the inkjet printer’s maximum stress is 5.8365 MPa, far below the allowable stress. Thus the effect of stress on the structure can be neglected in the inkjet printer optimization; b) the maximum deformation is for 0.016584 mm, which occurs in the upper position of the inkjet head module (as shown in Fig. 6). For an electronic circuit printing equipment of high precision, it should be further optimized; c) the first two natural frequencies of the inkjet printer are 46.721 Hz and 49.26 Hz, very close to the motor excitation frequency 50 Hz. It indicates they may cause resonance in operation. Therefore the natural frequency should be optimized.

5.2. Establishment of optimum model

5.2.2. Design variables

The inkjet printer dimensions depend on the specification of the PCBs, which usually are generally fixed. This study selects 8 parameters as the design variables for optimization design as specified in Table 2. According to previous analysis, these 8 parameters sway relatively great influence on the static and dynamic characteristics of the inkjet printer.

Table 2Initial values of design variables

Design variable	Initial value (mm)	Value range (mm)	Description
P1	100	90-110	Thickness of table
P2	100	90-110	Length of column along $X$ axis
P3	120	108-132	Length of column along $Y$ axis
P4	215	193.5-236.5	Length of column along $Z$ axis
P5	6	5.4-6.6	Thickness of base’s column
P6	3	2.7-3.3	Thickness of base’s top beam
P7	5	4.5-5.5	Thickness of base’s bottom beam
P8	20	18-22	Length of base’s bottom beam along $Y$ axis

Fig. 8The sensitivity of target to output variables

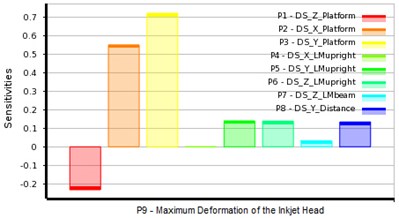
a) P9 – maximum deformation of the inkjet head

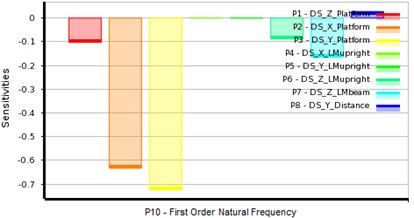
b) P10 – first order natural frequency

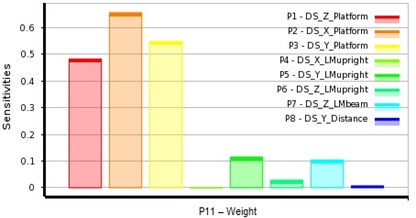
c) P11 – weight

5.2.3. The initial second order response surface model

For the polynomial response surface model fitting, the number of minimum experiment points is equal to the polynomial items. But it is general the case that the more the sample points are in the design space, the more accurate the response surface fitting is. So most optimization cases will choose more than double of the minimum experiment points. This study selected 8 design variables and 81 sample points. Then the response value of each sample was calculated by numerical simulation.

The effect of each design variable on the 3 output variables can be calculated by data statistics, as shown in Fig. 8. Design variables P3, P2 and P1 have great influence on the maximum deformation of inkjet head. But unlike p2 and p3, p1 has negative effect on the deformation. That is, the bigger p1 is, the less deformation occurs, thus the higher the stiffness is inkjet head. P3, P2, P7 and P1 are responsible for the change in the first order natural frequency. All these variables have negative correlation with the first order natural frequency, that is, when these design variables increase, the first order natural frequency decreases, hence the dynamic stiffness decreases. It can be explained that when these design variables increase, the bed weight increases and the gravity center of the inkjet printer goes higher. Design variables affecting the inkjet printer weight most are P1, P2 and P3.

To secure the accuracy of response surface, fitting curve was used to measure the model’s fitting precision. As shown in Fig. 9, sample points of the three optimization objectives (maximum deformation of the inkjet head, the first order natural frequency and inkjet printer weight) are located near the diagonal, that is, their multiple correlation coefficient approaches 1 and fitting degree of the response surface model is good.

Fig. 9Fitting curve

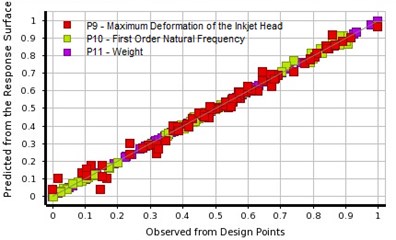
Table 3Comparison of conventional method and proposed method

Design variable	Original design	Conventional method	Proposed method
P1 / mm	100	93.52	90.01
P2 / mm	100	106.72	109.53
P3 / mm	120	117.1	108.01
P4 / mm	215	207.32	193.52
P5 / mm	6	5.45	5.9361
P6 / mm	3	3.24	3.0402
P7 / mm	5	5.16	4.6389
P8 / mm	20	21.74	20.935
Maximum deformation of the inkjet head P9 / mm	0.011788	0.00915	0.0078943
First order natural frequency P10 / Hz	46.721	56.164	63.665
Weight P11 / Kg	671.64	584.9	540.51

5.3. Optimization results and analysis

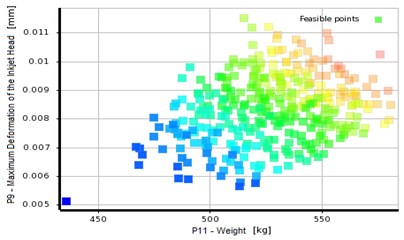
Cyclic approximation optimization technique of MOGA (NSGA-II) was applied to the optimization of the inkjet printer. Appropriate sample points were selected in the response surface model as initial samples for genetic algorithm. Here the number was set as 1000 and the calculation convergence criterion was 80 %. The maximum number of iterations was 20 while the three optimization objectives of maximum deformation of the inkjet head, the first order natural frequency and inkjet printer weight had the same weight ratio. Pareto optimal solution set was obtained after calculation as shown in Fig. 10. Table 3 compares one of the optimal solutions from the Pareto with the conventional optimization method.

Fig. 10Pareto optimal solution set of inkjet printer multi-objective optimization

a) P9-P11

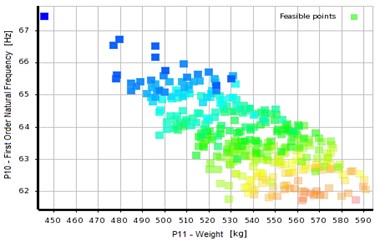
b) P10-P11

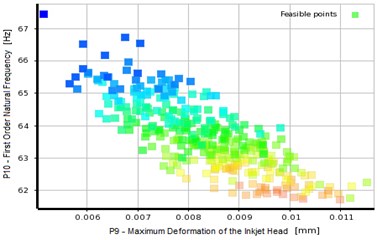
c) P10-P9

The optimization results reveal the inkjet printer weight reduces by 19.5 % and maximum deformation of the inkjet head decreases by 33 % after the multi-objective optimization of the column using response surface model. The first order natural frequency increases to 63.665 Hz, far from the servo motor excitation frequency 50 Hz. In addition, comparing with the conventional method, the optimal design method based on the response surface model is more reliable to obtain satisfactory results.