Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition

An, Xueli; Zeng, Hongtao

doi:10.21595/jve.2016.16553

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2016

Check for updates

Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition

Xueli An¹

Hongtao Zeng²

¹China Institute of Water Resources and Hydropower Research, Haidian District, Beijing 100038, China

²School of Power and Mechanical Engineering, Wuhan University, Wuhan, Hubei Province 430072, China

Corresponding Author:

Xueli An

Cite the article Download PDF

Downloads 1594

WoS Core Citations 7

CrossRef Citations 8

Abstract

For the non-stationary characteristics of the vibration signal of wind turbine’s roller bearing in fault condition, a bearing fault diagnosis method based on variational mode decomposition (VMD) and singular value decomposition (SVD) is proposed. The VMD method is used to decompose wind turbine’s roller bearing’s fault vibration signal into several components. These components are regard as initial feature vector matrix. The singular value decomposition of the matrix is done. The obtained singular value is used as the extracted bearing fault feature vectors. The probabilistic neural network is used as pattern recognition classifier to determine the working state and fault type of wind turbine roller bearings. The result of case study showed that the proposed method can effectively identify the working state and fault type of wind turbine roller bearings.

1. Introduction

Bearing is a key component of rotating machinery. It is also core component of wind turbine’s mechanical drive system. The non-bearing faults of gearbox and blade of mechanical drive system are found to be caused by bearing faults or may be reflected in the operating state of the bearing. So it is greatly significant for the fault diagnosis and operation maintenance of the entire mechanical drive system to real-time monitor the running state of bearing [1].

Wind turbines’ running has the features of random, intermittent and variable load, which makes wind turbine’s drive system’s fault vibration signal has the characteristics of nonstationarity, nonlinearity and complex modulation components. This results in the extraction difficulties of fault characteristics of wind turbine’s drive systems. The fault types are difficult to identify and particularly difficult to determine the fault location [2]. It has become the key for diagnosing the fault of rolling bearing, that how to extract fault feature information from the corresponding complex fault signals.

The original non-stationary vibration signal is decomposed, and then selecting the appropriate frequency bands or component to mine the information of signal. This is a commonly used means of fault diagnosis. Currently main analysis methods for non-stationary, non-linear signal frequency are wavelet transform, empirical mode decomposition (EMD), intrinsic time-scale decomposition (ITD), and so on. Recently, Dragomiretskiy and Zosso proposed a new method of signal decomposition, variational mode decomposition (VMD) [3]. This method can process non-linear, non-stationary signal, solve the defect of mode mixing which exist for EMD method.

Singular value decomposition (SVD) [4-6] technology has good stability and invariance. By means of reconstructing phase space attractor orbit matrix of fault signal, performing SVD, selecting appropriate singular value to reconstruct the fault signal, the fault features of fault signal can effectively extract. It has a good noise reduction effect, has been widely applied to the fault diagnosis of rotating machinery.

In this paper, a bearing fault diagnosis method of wind turbines based on VMD and SVD is proposed. VMD method is used to decompose vibration signal of rolling bearing into several components. Then these components are selected to form an initial feature vector matrix. The matrix is a complete characterization for the characteristic of the original vibration signal. The SVD is done for the initial feature vector matrix. The singular value of initial feature vector matrix is used as feature vector. The working states and fault types of wind turbine bearing can be determine based on the output of probabilistic neural network. Case study shows that this proposed method can effectively identify the operating states and fault types of wind turbine rolling bearings.

2. Variational mode decomposition

The variational mode decomposition (VMD) method is a new variation signal analyzing method [3], which can decompose a complex signal into a discrete number of modes $u_{k}$ centered around $ω_{k}$ . It can overcome some limitations of the Empirical mode decomposition (EMD) method.

The decomposition is given as follows:

1

\underset{u_{k}, ω_{k}}{m i n} \{\sum_{k} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2}\},

where $\sum_{k} u_{k} = f$ , $u_{k}$ ( $k =$ 1, 2, …, $K$ ) and $ω_{k}$ ( $k =$ 1, 2, …, $K$ ) are the sets of all nodes and their center pulsation.

Using Eq. (2) to set absolute integrable property of the signal:

2

L (u_{k}, ω_{k}, λ) = α \sum_{k} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2} + {‖f - \sum u_{k}‖}_{2}^{2} + ⟨λ, f - \sum u_{k}⟩ .

The alternate direction method of multipliers (ADMM) is used in VMD to produce different decomposed modes and the center frequency during each shifting operation. The ADMM is given as:

a) ADMM concept.

Initialize $u_{k}^{1}$ , $ω_{k}^{1}$ , $λ^{1}$ , $n \leftarrow 0$

Repeat

$n \leftarrow n + 1$

for $k = 1 : K$ do

Update $u_{k}$ :

3

u_{k}^{n + 1} \leftarrow \underset{ω_{k}}{a r g m i n} L (u_{1}^{n + 1}, \dots, u_{k - 1}^{n + 1}, u_{k}, u_{k + 1}^{n}, \dots, u_{K}^{n}, ω_{1}^{n}, \dots, ω_{K}^{n}, λ^{n})

end for

for $k = 1 : K$ do

Update $ω_{k}$ :

4

ω_{k}^{n + 1} \leftarrow \underset{ω_{k}}{a r g m i n} L (u_{1}^{n + 1}, \dots, u_{K}^{n + 1}, ω_{1}^{n + 1}, \dots, ω_{k - 1}^{n + 1}, ω_{k}, ω_{k + 1}^{n}, \dots, ω_{K}^{n}, λ^{n})

end for

Dual ascent:

5

λ^{n + 1} \leftarrow λ^{n} + τ (f - \sum_{k} u_{k}^{n + 1})

until convergence $\sum_{k} {‖u_{k}^{n + 1} - u_{k}^{n}‖}_{2}^{2} / {‖u_{k}^{n}‖}_{2}^{2} < ε$ .

b) Minimization w.r.t. $u_{k}$ .

The Eq. (3) is rewritten to update the modes $u_{k}$ , as follow:

6

u_{k}^{n + 1} = \underset{ω_{k} \in R}{a r g m i n} \{α {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2} + {‖f - \sum u_{i} + \frac{λ}{2}‖}_{2}^{2}\} .

The Parseval/Plancherel Fourier isometry under the L2 norm is used to find the solution of this quadratic optimization problem, as follows:

7

{\hat{u}}_{k}^{n + 1} = (\hat{f} - \sum_{i \neq k} {\hat{u}}_{i} + \frac{\hat{λ}}{2}) \frac{1}{1 + 2 α (ω - ω_{k})^{2}} .

c) Minimization w.r.t. $ω_{k}$ .

The minimization w.r.t. $ω_{k}$ can be done by using Eqs. (8)-(10):

8

ω_{k}^{n + 1} = \underset{ω_{k}}{a r g m i n} \{{‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2}\},

9

ω_{k}^{n + 1} = \underset{ω_{k}}{a r g m i n} \{\int_{0}^{\infty} (ω - ω_{k})^{2} {|{\hat{u}}_{k} (ω)|}^{2} d ω\},

10

ω_{k}^{n + 1} = \frac{\int_{0}^{\infty} ω {|{\hat{u}}_{k} (ω)|}^{2} d ω}{\int_{0}^{\infty} {|{\hat{u}}_{k} (ω)|}^{2} d ω},

where the new $ω_{k}$ is put at the center of gravity of power spectrum of the corresponding mode.

The obtained steps for the complete optimization of VMD, are given as:

Initialize ${\hat{u}}_{k}^{1}$ , $ω_{k}^{1}$ , ${\hat{λ}}^{1}$ , $n \leftarrow 0$

Repeat

$n \leftarrow n + 1$

for $k = 1 : K$ do

Update ${\hat{u}}_{k}$ for all $ω \geq 0$ :

11

{\hat{u}}_{k}^{n + 1} \leftarrow \frac{\hat{f} - \sum_{i < k} {\hat{u}}_{i}^{n + 1} - \sum_{i > k} {\hat{u}}_{i}^{n} + \frac{{\hat{λ}}^{n}}{2}}{1 + 2 α (ω - ω_{k})^{2}}

Update $ω_{k}$ :

12

ω_{k}^{n + 1} \leftarrow \frac{\int_{0}^{\infty} ω {|{\hat{u}}_{k}^{n + 1} (ω)|}^{2} d ω}{\int_{0}^{\infty} {|{\hat{u}}_{k}^{n + 1} (ω)|}^{2} d ω}

end for

Dual ascent for all $ω \geq 0$ :

13

{\hat{λ}}^{n + 1} \leftarrow {\hat{λ}}^{n} + τ (\hat{f} - \sum_{k} {\hat{u}}_{k}^{n + 1})

until convergence: $\sum_{k} {‖{\hat{u}}_{k}^{n + 1} - {\hat{u}}_{k}^{n}‖}_{2}^{2} / {‖{\hat{u}}_{k}^{n}‖}_{2}^{2} < ε$ .

3. Bearing fault diagnosis method of wind turbine based on VMD and SVD

VMD method can decompose a complex vibration signal $x (t)$ into a finite number of components ( $c_{1}$ , $c_{2}$ ,…, $c_{n}$ ). The obtained components can form an initial feature vector matrix, as:

14

A = [\begin{array}{l} c_{1} \\ c_{2} \\ ⋮ \\ c_{n} \end{array}] .

So the characteristics of the original vibration signal can be obtained by the feature extraction of initial feature vector matrix. In matrix theory, the singular value of matrix is an inherent feature of the matrix. It has good stability, that is, when the matrix elements have small changes, the change of the matrix’s singular value is little. Meanwhile, matrix’s singular value also has ratio invariance and rotation invariance. Therefore, the matrix’s singular value is in accord with the required stability, rotation invariance and ratio invariance of pattern recognition. It can effectively depict the characteristics of initial feature vector matrix. Consequently, the singular value of initial characteristic vectors matrix can be used as fault feature vector. And probabilistic neural network can be used to identify the work states and fault types of rotating machinery.

The concrete steps of bearing fault diagnosis method of wind turbine based on VMD and SVD are as follow:

(1) According to a certain sampling frequency $f_{s}$ , $N$ times samplings are made in different states of bearing as sample signals;

(2) Each vibration signal of each bearing state is decompose by VMD. The number of components of different vibration signals is different. Supposing the maximum component number is $n$ , if a sample’s component number is $n_{k}$ , and $n_{k} < n$ , then adding zero vector to make it has $n$ components, $c_{1}$ , $c_{2}$ ,…, $c_{n}$ . That is set the $c_{i} (t) = \{0\}$ ( $i = n_{k} + 1, n_{k} + 2, \dots, n$ );

(3) In accordance with the Eq. (14), each vibration signal in each state forms an initial feature vector matrix $A$ . The singular value decomposition of the matrix $A$ is done, the singular value $σ {}_{j}$ is obtained:

15

σ {}_{j} = [σ_{j}^{1}, σ_{j}^{2}, \dots, σ_{j}^{n}],

where $σ_{j}^{1} \geq σ_{j}^{2} \geq \dots \geq σ_{j}^{n}$ , $j$ represents different working condition of bearing;

(4) The probabilistic neural network is selected as fault classifier. The $σ_{j}$ is used as a feature vector of samples to input the probabilistic neural network and train it.

(5) The test signals are collected. In accordance with steps (2)-(3), an initial feature vector matrix $A_{x}$ is formed. The feature vectors $σ {}_{A, x}$ are calculated. They are input into probabilistic neural network (PNN). The operating states and fault types of rolling bearings are determined on the basis of the output of PNN.

4. Case study

The common faults of rolling bearing are inner race fault, outer race fault and roller fault. In this paper, four spherical roller bearings are selected to experiment. One is normal bearing, and the other three are set with inner race fault, outer race fault and roller fault, respectively. These faults are set by grooving using a linear cutting method. The slot width is 0.2 mm and the slot depth is 0.3 mm, as shown in Fig. 1 [1].

The experimental setup of direct-drive wind turbine is displayed in Fig. 2 [1]. In the system, the wind is produced by a wind tunnel under laboratory conditions. In order to produce wind of different speeds, the axial fan of 15 kW is controlled by a variable frequency drive. When the turbine blades capture wind energy from wind tunnel and start moving, then they drive the main shaft connected with the generator to spin and produces AC electricity. Direct-drive wind turbine main shaft is supported by two dual-row spherical roller bearing (22206-type). The defect bearings are installed in the near wind wheel. The bearing vibration signal is picked up by an acceleration sensor installed in defect bearing. A test system is developed to monitor wind turbine’s operation condition.

Fig. 1View of spherical roller bearing in normal and three faults conditions

a) Normal bearing

b) Outer race fault

c) Inner race fault

d) Roller fault

Fig. 2Test stand of direct-drive wind turbine

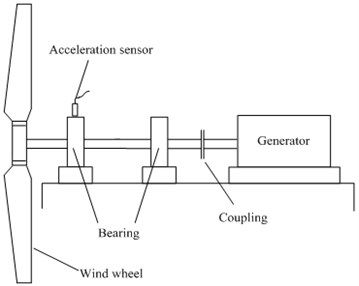
a) Test stand schematic diagram

b) Test stand picture

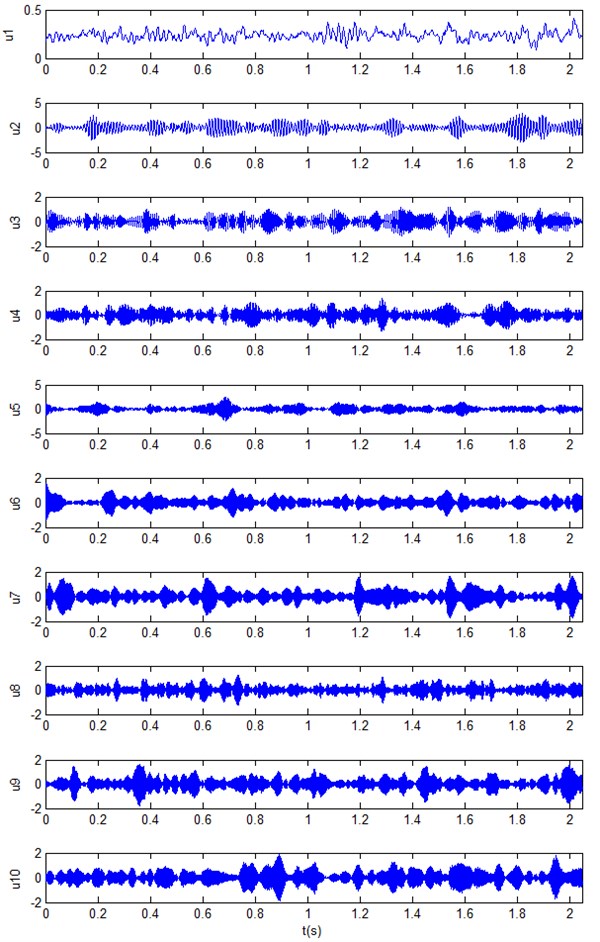
The bearing vibration signals of wind turbine in four working states (normal state, inner race fault, outer race fault and roller fault) are collected. For each state, 40 sets data are collected. The rotational speed of experiment is 260 r/min, the sampling frequency is 2000 Hz. Fig. 3 gives vibration acceleration signal of rolling bearing with roller fault. Fig. 4 gives the results of VMD on the fault signal, there are ten components. It can be seen from the figure that VMD can decompose the non-stationary vibration signal of rolling bearing fault into the sum of several stationary components, different components contain different time scales. Therefore, after comparison and analysis, these components are selected to form an initial feature vector matrix $A$ .

Fig. 3Vibration acceleration signal of rolling bearing with roller fault

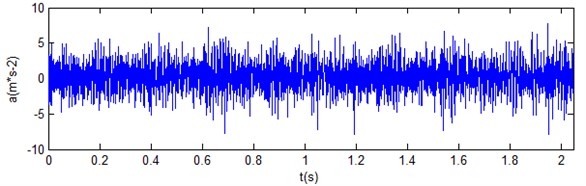
Fig. 4Results of VMD on fault signal

The bearing vibration acceleration signals of wind turbine in four states (normal state, inner race fault, outer race fault and roller fault) are collected. For each state, 40 sets data are collected. The total data are 4×40 = 160 sets. For the 160 sets data, 80 sets data are randomly selected (20 sets data for each state) as the standard input samples. They are input to probability neural network for training. The remaining 80 sets data are used as the test sample to verify the method. It can be found that the identification results are matched with the actual faults. Table 1 shows the identification results of 12 sets test samples which includes randomly selected three normal state data, three inner race fault data, three outer race fault data and three roller fault data. The ‘√’ indicates accurate identification; the ‘×’ indicates false recognition.

Table 1Diagnosis results of rolling bearings fault based on VMD–SVD or wavelet-SVD

No.	State of test signals	Diagnosis method	Feature vector										Diagnosis results
No.	State of test signals	Diagnosis method	Singular value $σ {}_{A, x}$										Diagnosis results
1	Normal condition	VMD-SVD	35.32	33.23	30.30	24.31	24.00	20.25	17.24	16.27	15.18	14.59	√
1	Normal condition	wavelet-SVD	58.00	56.10	49.18	35.78	15.36	10.83	2.98	2.67	2.42	1.96	√
2	Normal condition	VMD-SVD	34.97	33.39	30.49	24.69	23.82	20.44	17.40	16.13	15.41	14.22	√
2	Normal condition	wavelet-SVD	58.17	56.56	48.75	37.00	14.70	11.29	2.67	2.32	1.55	1.38	√
3	Normal condition	VMD-SVD	34.80	33.74	30.38	25.13	24.91	20.03	17.08	16.00	15.27	14.20	√
3	Normal condition	wavelet-SVD	58.76	56.44	49.79	35.27	15.77	11.70	2.72	2.36	1.54	1.39	√
4	Outer race fault	VMD-SVD	40.52	35.91	28.38	27.57	26.26	24.34	22.34	21.86	19.76	14.71	√
4	Outer race fault	wavelet-SVD	77.06	64.85	52.08	47.37	15.07	12.70	5.62	3.62	2.78	2.09	√
5	Outer race fault	VMD-SVD	41.55	33.39	28.00	26.63	25.64	22.35	22.16	20.54	17.63	14.11	√
5	Outer race fault	wavelet-SVD	77.21	66.69	52.79	48.53	26.65	16.23	15.46	11.69	8.36	6.11	√
6	Outer race fault	VMD-SVD	41.22	33.22	27.93	27.20	25.42	23.75	22.07	21.43	19.97	14.08	√
6	Outer race fault	wavelet-SVD	77.02	66.54	52.16	49.76	18.60	16.97	8.56	6.47	5.88	4.78	√
7	Inner race fault	VMD-SVD	36.65	33.25	30.87	29.29	28.71	25.23	24.57	22.98	18.22	14.87	√
7	Inner race fault	wavelet-SVD	93.23	64.17	57.03	47.38	14.84	14.30	3.80	2.56	1.93	1.18	√
8	Inner race fault	VMD-SVD	36.70	33.22	30.59	29.11	28.34	25.33	23.97	22.68	17.65	14.94	√
8	Inner race fault	wavelet-SVD	92.89	64.59	58.92	44.41	15.37	14.94	5.43	4.77	4.45	3.83	√
9	Inner race fault	VMD-SVD	36.25	33.35	30.72	28.89	28.44	25.50	24.01	22.50	17.38	14.83	√
9	Inner race fault	wavelet-SVD	92.81	64.08	57.30	44.27	14.90	14.74	4.14	3.75	2.92	2.21	√
10	Roller fault	VMD-SVD	53.82	32.98	32.36	28.23	26.35	25.77	23.55	20.91	20.21	15.45	√
10	Roller fault	wavelet-SVD	71.02	67.72	59.33	56.36	17.03	16.77	4.23	2.88	2.47	1.77	√
11	Roller fault	VMD-SVD	53.85	33.08	28.89	27.88	25.64	24.70	21.98	20.10	18.63	15.62	√
11	Roller fault	wavelet-SVD	70.25	67.23	59.20	56.24	16.50	15.30	4.33	2.56	0.63	0.62	√
12	Roller fault	VMD-SVD	54.49	33.05	32.34	27.74	26.40	25.57	23.44	21.68	20.58	15.41	√
12	Roller fault	wavelet-SVD	72.82	69.21	58.33	56.57	15.88	15.44	4.71	4.48	3.23	2.83	√

A ‘db4’ wavelet is used to decompose the same bearing vibration signals. For purposes of comparison, the decomposition level (ten levels) of wavelet is same as the VMD. According to the steps (2) to (5) in Section 3, the diagnosis process is same as above. The recognition accuracy rate is 100 %. Table 1 gives twelve data sets of feature vectors based on wavelet and SVD (wavelet-SVD) in four states.

It can be seen from the diagnosis results that VMD and wavelet transform both can be used to pretreat bearing vibration signal, and then through computing these obtained components’ singular values to extract the fault information of these obtained components as fault characteristic parameters to recognize the bearing fault. The two diagnosis methods both have high diagnostic accuracy. The stability of the characteristic parameters of bearing different signals in the same state is analyzed. It can be seen that the extracted characteristic parameters based on VMD-SVD have high stability and small discreteness. This can better ensure the credibility and accuracy of diagnostic results. The extracted characteristic parameters based on wavelet-SVD have poor stability and large discreteness.

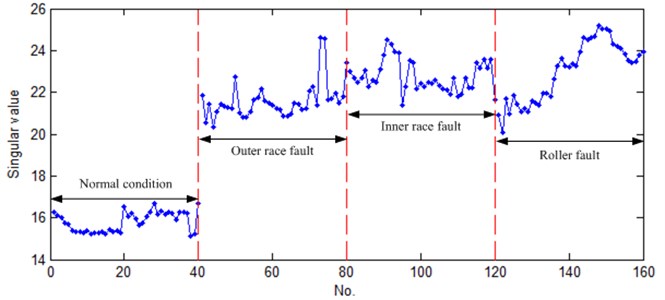
It can be seen in Table 1, the obtained fifth singular value based on wavelet-SVD of the fifth test sample is 26.65, but the obtained fifth singular values of the fourth and sixth test samples are 15.07 and 18.60, respectively. The difference of the three singular values is big. This means their large discreteness. The obtained seventh and eighth singular values based on wavelet-SVD of the fourth, fifth and sixth have same conclusions. The eighth singular values of 160 data sets with four bearing states are shown in Fig. 5. It can be seen from this figure that when bearing with normal condition, the eighth singular values of 160 data sets are mainly focused on around 16. When bearing with outer race fault, inner race fault or roller fault, the eighth singular values of 160 data sets are obviously greater than 20. These mean that the singular value has high sensitivity for the changes in the state of the spherical roller bearing.

Fig. 5The eighth singular values of 160 data sets with four bearing states

5. Conclusions

In this paper, VMD method is used to decompose vibration signal of wind turbine rolling bearing. The obtained components form an initial feature vector matrix. Then singular value decomposition of initial feature vector matrix is done to extract the characteristic of vibration signal. The acquired characteristics vector can fully characterize the feature of vibration signal. Finally, the singular value of initial feature vector matrix is selected as the input parameters of probabilistic neural network to classify the vibration signal. Case study shows that the proposed diagnosis method, which based on VMD and SVD, can effectively identify the working states and fault types of wind turbine rolling bearing.

References

An Xueli, Jiang Dongxiang, Chen Jie, Liu Chao Application of the intrinsic time-scale decomposition method to fault diagnosis of wind turbine bearing. Journal of Vibration and Control, Vol. 18, Issue 2, 2012, p. 240-245.

Publisher
An Xueli, Jiang Dongxiang, Li Shaohua, Zhao Minghao Application of the ensemble empirical mode decomposition and Hilbert transform to pedestal looseness study of direct-drive wind turbine. Energy, Vol. 36, Issue 9, 2011, p. 5508-5520.

Publisher
Dragomiretskiy K., Zosso D. Variational Mode Decomposition. IEEE Transactions on Signal Processing, Vol. 62, Issue 3, 2014, p. 531-544.

Publisher
Wang Zhipeng, Lu Chen, Wang Zili, et al. Fault diagnosis and health assessment for bearings using the Mahalanobis-Taguchi system based on EMD-SVD. Transactions of the Institute of Measurement and Control, Vol. 35, Issue 6, 2013, p. 798-807.

Publisher
Li Limin, Wang Zhongsheng, Jiang Hongkai Storage battery remaining useful life prognosis using improved unscented particle filter. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, Vol. 229, Issue 1, 2015, p. 52-61.

Publisher
Chen Xiaoan, Liu Xing, Dong Shaojiang, et al. Single-channel bearing vibration signal blind source separation method based on morphological filter and optimal matching pursuit (MP) algorithm. Journal of Vibration and Control, 2013.

Publisher

Cited by

Recent Advancements in Fault Diagnosis of Spherical Roller Bearing: A Short Review

(2024)

Development of gear fault identification of wind turbine’s transmission system based on VMD and FNN

Li Cao | Wenlei Sun

(2024)

Bearing Fault Classification Using Improved Antlion Optimizer and Extreme Learning Machine

(2022)

Artificial Intelligence-Based Technique for Fault Detection and Diagnosis of EV Motors: A Review

(2022)

Fault Diagnosis of Induction Motors Under Untrained Loads With a Feature Adaptation and Improved Broad Learning Framework

Pak Kin Wong | Jiang Sai Biao

(2022)

Fault Diagnosis of Hydraulic Generator Bearing by VMD-Based Feature Extraction and Classification

Xuanrong Tang | Bian Hu | He Wen

(2021)

A Review on Variational Mode Decomposition for Rotating Machinery Diagnosis

M. Firdaus Isham | M. Salman Leong | M. H. Lim | M. K. Zakaria | Lim Meng Hee

(2019)

A Fault Diagnostic Method for Induction Motors Based on Feature Incremental Broad Learning and Singular Value Decomposition

Sai Biao Jiang | Pak Kin Wong | Yan Chun Liang

(2019)

About this article

Received

13 October 2015

Accepted

17 February 2016

Published

30 September 2016

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2016.16553

Keywords

wind turbine

spherical roller bearing

fault diagnosis

variational mode decomposition

singular value decomposition

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 51309258, 51479076).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

Rolling bearing fault diagnosis based on variational mode decomposition and weighted multidimensional feature entropy fusion

Na Lei, Feihu Huang, Chunhui Li

Research article

2023 09 08

Research on fault diagnosis method of bearing based on parameter optimization VMD and improved DBN

Yingqian Sun, Zhenzhen Jin

Research article

2022 11 30

Rolling bearing weak fault diagnosis utilizing successive variational mode decomposition with sparsity index reconstructing strategy

Lijie Jiang, Hongchao Wang, Wenliao Du

Research article

2022 05 15

The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage

Xing Yuan, Huijie Zhang, Hui Liu

X. An and H. Zeng, “Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition,” Journal of Vibroengineering, Vol. 18, No. 6, pp. 3548–3556, Sep. 2016, https://doi.org/10.21595/jve.2016.16553

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16553
UR  - https://doi.org/10.21595/jve.2016.16553
TI  - Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition
T2  - Journal of Vibroengineering
AU  - An, Xueli
AU  - Zeng, Hongtao
PY  - 2016
DA  - 2016/09/30
PB  - JVE International Ltd.
SP  - 3548-3556
IS  - 6
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{An_2016,
	doi = {10.21595/jve.2016.16553},
	url = {https://doi.org/10.21595/jve.2016.16553},
	year = 2016,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {6},
	pages = {3548--3556},
	author = {Xueli An and Hongtao Zeng},
	title = {Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. An and H. Zeng, “Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition,” Journal of Vibroengineering, vol. 18, no. 6, pp. 3548–3556, Sep. 2016, doi: 10.21595/jve.2016.16553.

Copy IEEE

Copied to clipboard!

An, Xueli, and Hongtao Zeng. “Fault Diagnosis Method for Spherical Roller Bearing of Wind Turbine Based on Variational Mode Decomposition and Singular Value Decomposition.” Journal of Vibroengineering 18, no. 6 (September 30, 2016): 3548–56. https://doi.org/10.21595/jve.2016.16553.

Copy Chicago

Copied to clipboard!

Fault diagnosis method for spherical roller bearing of wind turbine based on variational mode decomposition and singular value decomposition

Abstract

1. Introduction

2. Variational mode decomposition

3. Bearing fault diagnosis method of wind turbine based on VMD and SVD

4. Case study

5. Conclusions

References

Cited by

About this article

Related Articles