Effect of sink flow on dual-valve electro-hydraulic excitation system

Meng, Zhen; Wu, Chuan-yu; Ni, Jing

doi:10.21595/jve.2016.16589

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2016

Check for updates

Effect of sink flow on dual-valve electro-hydraulic excitation system

Zhen Meng¹

Chuan-yu Wu²

Jing Ni³

^{1, 2}Zhejiang Sci-Tech University, School of Mechanical Engineering and Automation, Hangzhou, China

³Hangzhou Dianzi University, School of Mechanical Engineering, Hangzhou, China

Corresponding Authors:

Chuan-yu Wu, Jing Ni

Cite the article Download PDF

Downloads 1342

WoS Core Citations 2

CrossRef Citations 2

Abstract

In this study, the main goal is to investigate the displacement gain characteristics of novel dual-valve Electro-Hydraulic Excitation system (EHES). Relative to conventional system, the dual-valve system can improve the amplitude range, but the range is always affected by some nonlinear factors. In order to analysis on the issue, a nonlinear mathematical model of dual-valve EHES is established based on Bernoulli and classical electro-hydraulic servo equation. Then, the results of numerical simulations by using of the MATLAB/Simulink software are compared with experimental results. Simulation and experimental results show that the sink flow mainly influences on the flow dynamic characteristics of dual-valve EHES. Because of that, dual-valve EHES only can improve 50 %-70 % of displacement within 5 to 50 Hz of excitation frequency and 45 %-80 % of displacement amplitude within 20 % to 100 % of command value.

1. Introduction

The Electro-Hydraulic Excitation system (EHES) is a key component for modern simulation test of automobile or mobile machines and the seismic fatigue test of dams or tall buildings. The system is mainly worked by the reciprocating motion of valve spool, which varies the flow in cycles (Fig. 1). However, the vibration amplitude is restricted within a narrow range due to the characteristic of valve port [1]. Therefore, the optimization of vibration performance for EHES has been the focus of both academic and industrial field.

In conventional EHES, it usually adopts slide or nozzle flapper valve to control the hydraulic cylinder or torque motor [2]. In order to improve the response characteristics of the hydraulic valve, Han et al., Zhang et al., Lian et al. and Wang et al. replaced the slide valve with rotary valve [3-6]. Liu et al. and Ruan et al. proposed a special valve structure with two degree of freedom [7, 8]. For purpose of optimizing the output waveform, a series of controller was designed by introducing Lyapunov function method, self-adjustment quantitative feedback theory, varying error controls strategy, neurodynamic optimization and other mathematical method [9-16]. For the sake of researching the vibration performance, Han et al. simulated the vibration characteristics of a new electro-hydraulic vibrator by using the AMESim software [17]. Wei et al. and Kou et al. summarized the law of pressure pulsation [18, 19]. However, the studies all above have only focused on the frequency range and stability of the excited system, and ignored the displacement amplitude range. A little paper introduced the unique advantages of multi-valve system in enhancing displacement amplitude ranges. Ren et al. proposed the offset valve [20]. Chiang et al. applied the parallel switching valve to control the vertical vibration system [21]. But they only focused on the application effect, lacking studies on the excitation mechanism. In view of this, this article will introduce a novel EHES with dual-valve in order to enhance the vibrator performance, and investigate the vibration characteristics of the system, especially in the aspect of displacement amplitude.

In the first part of the paper, a mathematical model of dual-valve EHES is presented. The system is mainly described by Bernoulli and classical flow characteristic equation. Then, the effect of sink flow on displacement gain characteristic of the system within various vibration parameters is analyzed by using the MATLAB/Simulink software. Meanwhile, the test platform is set up to validate the calculation results. The simulation and experimental data are presented and discussed in third part. Finally, the conclusions are given from a number of comparisons between the experimental and the numerical results.

2. Dual-valve EHES model

The dual-valve EHES is shown in Fig. 2, which consists of two parallel servo valves and a vibration cylinder. Similar to conventional system, the dual-valve system also relay on the cyclic flow to achieve the continuous reciprocating vibrations. For the purpose of improving the displacement amplitude, the valves must be controlled by the same exciting signal.

Fig. 1Electro-hydraulic excitation system

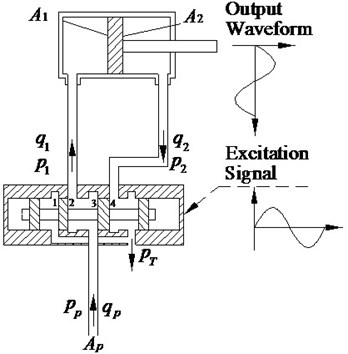
Fig. 2Dual-Valve EHES

2.1. Valve port flow

As shown in Fig. 2, the valve spool will move left when the excitation signal is positive, and the high pressure oil will flow into the left cavity of cylinder. In contrast, the high pressure oil will flow into right cavity when the signal is negative. Therefore, the flow equation of valves is:

1

\{\begin{array}{l} q_{i 1} = C_{d} ω_{i} x_{v i} \sqrt{\frac{2 (p_{p i} - p_{i 1})}{ρ}}, \\ q_{i 2} = C_{d} ω_{i} x_{v i} \sqrt{\frac{2 p_{i 2}}{ρ}}, \end{array} \begin{array}{l} x_{v i} > 0 \end{array},

2

\{\begin{array}{l} q_{i 1} = C_{d} ω_{i} x_{v i} \sqrt{\frac{2 p_{i 1}}{ρ}}, \\ q_{i 2} = C_{d} ω_{i} x_{v i} \sqrt{\frac{2 (p_{p i} - p_{i 2})}{ρ},} \end{array} \begin{array}{l} x_{v i} < 0 \end{array},

where $p_{p i}$ is the supply pressure of $i$ th valve, $p_{i 1}$ and $p_{i 2}$ is the pressure of flowing out and in $i$ th valve. $q_{i 1}$ and $q_{i 2}$ is the flow out and in $i$ th valve ( $i =$ 1, 2).

2.2. Sink flow model

As shown in Fig. 2, sink flow will appear on the tee joint when the oil flows to cylinder. According to Bernoulli’s equation:

3

\{\begin{array}{l} p_{11} + 0.5 ρ {(\frac{q_{11}}{A_{11}})}^{2} = p_{1} + 0.5 ρ {(\frac{q_{1}}{A_{1}})}^{2}, \\ p_{21} + 0.5 ρ {(\frac{q_{21}}{A_{21}})}^{2} = p_{1} + 0.5 ρ {(\frac{q_{1}}{A_{1}})}^{2}, \end{array}

4

\{\begin{array}{l} p_{12} + 0.5 ρ {(\frac{q_{12}}{A_{12}})}^{2} = p_{2} + 0.5 ρ {(\frac{q_{2}}{A_{2}})}^{2}, \\ p_{22} + 0.5 ρ {(\frac{q_{22}}{A_{22}})}^{2} = p_{2} + 0.5 ρ {(\frac{q_{2}}{A_{2}})}^{2}, \end{array}

where $p_{1}$ and $p_{2}$ is the pressure of the left and right cavity. The flow into and out of the cylinder is $q_{1}$ and $q_{2}$ . $A_{1}$ is the area of piston, and $A_{2}$ is the cross sectional area of right cavity. $A_{i 1}$ and $A_{i 2}$ are the cross sectional area of pipeline ( $i =$ 1, 2):

5

\{\begin{array}{l} q_{1} = (C_{d} ω_{1} x_{v 1} \sqrt{\frac{2 (p_{p} - p_{1})}{ρ}} + C_{d} ω_{2} x_{v 2} \sqrt{\frac{2 (p_{p} - p_{1})}{ρ}}), & x_{v 1} > 0, \\ q_{2} = (C_{d} ω_{1} x_{v 1} \sqrt{\frac{2 p_{2}}{ρ}} + C_{d} ω_{2} x_{v 2} \sqrt{\frac{2 p_{2}}{ρ}}), & x_{v 2} > 0, \end{array}

6

\{\begin{array}{l} q_{1} = (C_{d} ω_{1} x_{v 1} \sqrt{\frac{2 p_{1}}{ρ}} + C_{d} ω_{2} x_{v 2} \sqrt{\frac{2 p_{1}}{ρ}}), & x_{v 1} < 0, \\ q_{2} = (C_{d} ω_{1} x_{v 1} \sqrt{\frac{2 (p_{p} - p_{2})}{ρ}} + C_{d} ω_{2} x_{v 2} \sqrt{\frac{2 (p_{p} - p_{2})}{ρ}}), & x_{v 2} < 0 . \end{array}

The first equation of Eq. (3) multiplies by $q_{11}$ , and the second one multiplies by $q_{21}$ . Then, substituting Eq. (1) into Eq. (3) yields Eq. (5). The first equation of Eq. (4) multiplies by $q_{12}$ , and the second one multiplies by $q_{22}$ . Then, substituting Eq. (1) into Eq. (4) yields Eq. (6). Due to the connection pipe is hard and short, the energy loss can be neglected. Therefore, the sink flow equation can be expressed as follow.

2.3. Dual-valve coupling model

According to Fig. 2, the flow into and out of cylinder can be expressed by:

7

\{\begin{array}{l} q_{1} = C_{n p} (p_{1} - p_{2}) + C_{e p} p_{1} + \frac{V_{1}}{β_{e}} {\dot{p}}_{1} + {\dot{V}}_{1}, \\ q_{2} = C_{n p} (p_{1} - p_{2}) - C_{e p} p_{2} - \frac{V_{2}}{β_{e}} {\dot{p}}_{2} + {\dot{V}}_{2} . \end{array}

According Newton’s second law, the equilibrium equation of piston is given by:

8

A_{1} p_{1} - A_{2} p_{2} = m {\ddot{x}}_{p} + B_{p} {\dot{x}}_{p} + F_{L} .

Combing Eqs. (5)-(8), the dual-valve EHES are defined mathematically as follows:

9

\{\begin{array}{l} K C_{d} ω (x_{v 1} + x_{v 2}) \sqrt{(α_{1} p_{p} + α_{2} p_{L})} = \frac{L_{s} A_{1} (1 + η^{4})}{2 (1 + η^{3}) β_{e}} {\dot{p}}_{L} + A_{1} {\dot{x}}_{p}, \\ A_{1} p_{L} = m {\ddot{x}}_{p} + B_{p} {\dot{x}}_{p}, \end{array}

where:

K = \sqrt{\frac{2}{ρ (1 + η^{3})}},

α_{1} = \{\begin{array}{l} 1, & x_{v 1} > 0, x_{v 2} > 0, \\ \frac{η^{3}}{(1 + η^{2})^{2}}, & x_{v 1} < 0, x_{v 2} < 0, \end{array}

α_{2} = \{\begin{array}{l} - 1, & x_{v 1} > 0, x_{v 2} > 0, \\ \frac{1}{(1 + η^{2})^{2}}, & x_{v 1} < 0, x_{v 2} < 0 . \end{array}

3. Simulation and experiment

3.1. Simulation test

The simulations have two parts. Part I: it is mainly to investigate the effect of sink flow on characteristics of output displacement. Firstly, the characteristics of the system with sink flow are numerically calculated by using Matlab/Simulink software. Then, the results are compared with the output displacement of the model without sink flow. Part II: it is mainly to analysis the relationship between the sink flow and the exciting parameters. Firstly, it is to simulate and analysis the output displacement of dual-valve EHES with and without sink flow under various excitation frequencies. Then, the results are compared with the output displacement under various command values of valve (valve opening).

Especially, the model with and without sink flow are simulated under the same condition. The main parameters in the simulation are shown in Table 1.

Table 1Main parameter of the system

Parameter	Symbol	Value	Unit
Voltage Gain	$K_{v}$	0.1	mm/V
Valve port area of gradient	$W$	5.65	mm
Valve flow coefficient	$C_{d}$	0.6
Working pressure	$p_{p}$	6	MPa
Oil density	$ρ$	900	kg/m³
Piston diameter	$A_{1}$	60	mm²
Rod diameter	$A_{2}$	35	mm²
Cylinder stroke	$L_{s}$	100	mm
Asymmetric ratio	$Η$	0.583
Oil elastic modulus	$β_{e}$	700	MPa
Viscous damping coefficient	$B_{p}$	300	N·s/m
Total mass	$M$	10	Kg
Vibration frequency	$f$	5-50	Hz
Command value of valve	$x_{v}$	20, 40, 60, 80, 100	%

According to the equations above, the dual-valve EHES model without sink flow can be simply considered the superposition of single valve system. And, the single valve EHES can be expressed by:

10

\{\begin{array}{l} C_{d} ω x_{v} \sqrt{\frac{2 (p_{p} + λ p_{L})}{ρ (1 + η^{3})}} = \frac{L_{s} A_{1} (1 + η^{4})}{2 (1 + η^{3}) β_{e}} {\dot{p}}_{L} + A_{1} {\dot{x}}_{p}, \\ A_{1} p_{L} = m {\ddot{x}}_{p} + B_{p} {\dot{x}}_{p}, \end{array}

where, if $x_{v} >$ 0, then $λ =$ –1; $x_{v} <$ 0, then $λ =$ 1.

In order to intuitively reflect the effect of sink flow on the system, this paper introduce the bias gain, which is defined as follow:

11

g a i n_{e} = g a i n_{s} - g a i n_{d},

where the $g i a n_{s}$ is the displacement gain without sink flow. The $g i a n_{d}$ is the gain with sink flow. And the $g i a n_{s}$ can be expressed as follow:

12

g a i n_{s} = \frac{x_{p s} - x_{s}}{x_{s m}},

where $x_{p s}$ is the displacement of the system without sink flow. $x_{s}$ is the displacement of single valve model. $x_{s m}$ is the maxim value of $x_{s}$ .

The $g a i n_{d}$ can be expressed by:

13

g a i n_{d} = \frac{x_{p d} - x_{s}}{x_{s m}},

where $x_{p d}$ is the displacement of the system with sink flow.

3.2. Experimental test

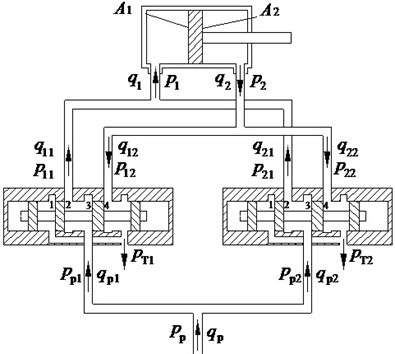
In order to verify the simulation results, the experimental tests also have two parts, and the goal of each part is the same as the simulation. As shown in the Figs. 3-4, the experimental platform of dual-valve EHES has been developed and designed, which is divided into three modules: excitation controller, vibration generator and measuring instrument. The controller sent the same signals to dual valve at the same time, which used is S7-300 PLC produced by SIMENS, and it is programmed by PCC using STEP 7 software. The generator, including servo valves and excitation cylinder, excites vibration waveform following the signals. The servo valves used are 4WSE2EM6 produced by Rexroth, which are controlled by the voltage signal. The excitation cylinder is special customized by referencing the CD 210 B63/35-100. The instrumentation is mainly measuring for vibration displacement. The measuring instrument is VIBXPERT II VIB5.325 produced by PRUFTECHNIK, and the vibration sensor is VIB 6.142R, which is mounted on the top of the piston rod by magnetic base. And the specifications of the system are summarized in Table 2.

Table 2Experimental instruments

Instrument	Model	Range	Signal
Servo valve	4WSE2EM6	25 L/min	± 10 V
Program controller	S7-300 CPU 314	–	–
A/D module	SM332	± 27648	± 10 V
FFT data collector and signal analyzer	VIB5.325	10 KHz	–
Mobile accelerometer	VIB 6.142R

To compare the simulation results, the experimental parameters are the same and are shown in Table 1.

Fig. 3EHES controlled by dual-valve

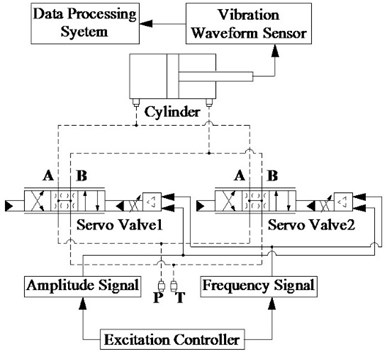
Fig. 4Experiment system

4. Results and discussion

Fig. 5 shows the amplitude gain of displacement from simulation part I. It can be seen that the gains without sink flow by numerically simulation are almost from –1 to 1. And the gains with sink flow are only from –0.52 to 0.52. It indicates that the sink flow restricts the ability of dual-valve EHES on enhancing displacement range. As can be seen from Fig. 5, the bias gains are obviously asymmetry in one period. The characteristic of asymmetry means the sink flow lead to saturated pressure appearing earlier than that of the system without sink flow when piston moving to the end of cylinder. Therefore, the sink flow mainly affects the characteristics of cavity pressure by simulation analysis.

Fig. 5Simulation results

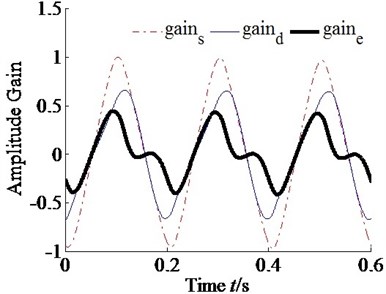
Fig. 6Experimental results

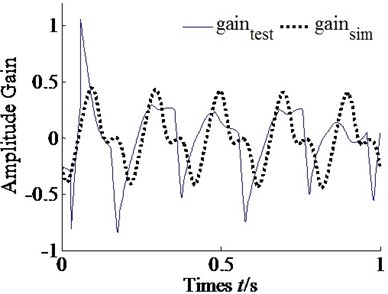
As Fig. 6 shown, the curve $g a i n_{s i m}$ represents the simulation results of bias gain. The curve $g a i n_{t e s t}$ represents the experimental results. By comparing two curves, it is shown that the experimental data have been validated the simulation results. The asymmetry characteristics of displacement gain also exist in actual system. As the curve $g a i n_{t e s t}$ shown, the positive data are more smoothly, and the negative data are more acute. It means that the sink flow characteristic more obvious on small cavity of cylinder than big. That is the smaller volume of cavity, the sink flow effect more obvious.

Therefore, based on the results of test part I, the conclusion is that the sink flow affects mainly on the pressure characteristics of cylinder, and then restricts the flow of dual-valve EHES. Thus, the dual-valve EHES cannot further enhance displacement range.

Fig. 7(a) and (b) show the bias gain of displacement under various frequencies from test part II. Fig. 8 shows the peak values of bias gain. As Fig. 7(a) and (b) shown, it can be seen that the trend of experimental data is similar to the simulation results in a certain period. The bias gain would not vanish as excitation frequency change. As Fig. 8 shown, the curve of simulation results fluctuates smoothly, but the curve of experimental data rise slowly. The peak values of bias gain are steady in general. It means the excitation frequencies have effect on bias gain, but the effect is not very significant. Thus, the effect of sink flow on displacement gain under various frequencies is not obvious. The reason is that the high frequency movement of spool induces the pressure transient on valve port. In fact, the characteristic of pressure would exhibit the displacement amplitude range of single-valve system. But it has a relatively minimal impact on sink flow.

Fig. 7Bias gain with varying frequency

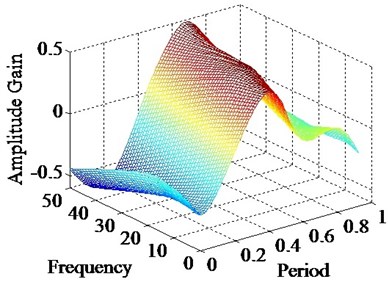
a)

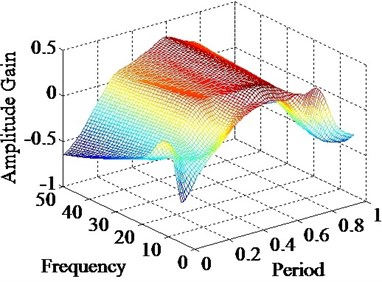
b)

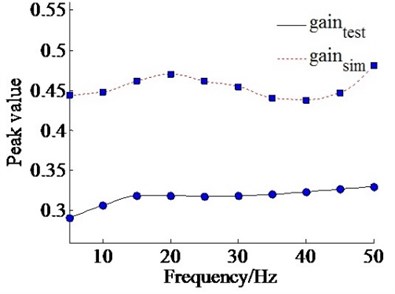
As Fig. 8 shown, the peak values of experimental data are generally smaller than simulation results, which just vary from 0.28 to 0.34. It means the mathematic model of dual-valve EHES only can explain the trend of the dynamic characteristic of bias gain under various frequencies, but not quantitative analysis of actual displacement gain. The reason is that the actual system has more nonlinear and uncertainty parameters than simulation model.

Fig. 8Peak gain with varying frequency

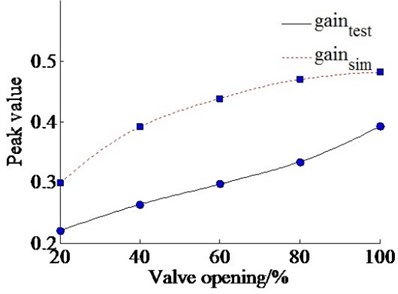
Figs. 9(a) and (b) show the bias gain under various command value of valve from test part II. Fig. 10 shows the peak values of bias gain arise with varying command value. As Fig. 9(a) and (b) shown, it can be seen that the trend of experimental data is also similar to the simulation results. The bias gain would not vanish as command value change as well. Therefore, the sink flow is the generic characteristics of dual-valve EHES. As Fig. 10 shown, the curve of simulation results rises from 0.3 to 0.46, and the curve of experimental data rises from 0.2 to 0.37. It means that the more command value, the bias gain more obvious. The reason is that the more command value of valve induces the more flow on valve port. And the characteristics of flow have a relatively obvious impact on sink flow comparing to the results under various frequencies. Otherwise, as Fig. 10 shown, the experimental data are also smaller than simulation results.

Therefore, the command values of valve mightily influence the bias gain comparing to excitation frequency. That is the characteristic of flow directly affects the sink flow; and then it further restricts the displacement gain of the dual-valve system. But the command values can promote the displacement amplitude of single-valve system increase. In a word, sink flow influence on the displacement gain of dual-valve system. But the varying excitation parameters can affect both the bias gain and the output amplitude of the system. Thus, the excitation parameters must be chosen reasonably to reduce sink flow influence and achieve a better performance on the output displacement of the dual-valve system.

Fig. 9Bias gain with varying command value

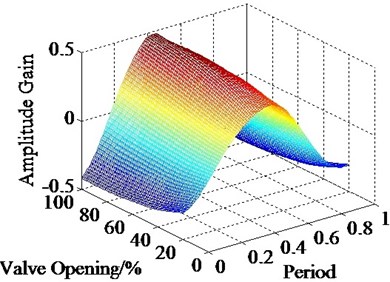
a)

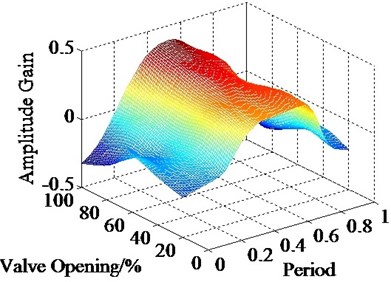
b)

Fig. 10Peak gain with varying command value

5. Conclusion

From the experimental data and simulation results, the conclusions are summarized as follows:

1) A mathematical model for studying the sink flow effect of dual-valve EHES has been presented. Considering the simulation and test results, the dual-valve EHES only can improve 50 %-80 % displacement ranges compared to the system without sink flow under pressure 6 MPa.

2) The sink flow affects mainly on the pressure characteristics of cylinder, and then restricts the ability of dual-valve EHES on enhancing displacement range.

3) The bias gain, which intuitively reflects the effect of sink flow on the system, varies from 0.29 to 0.34 when the excitation frequencies are from 5 Hz to 50 Hz, and it varies from 0.2 to 0.38 when the command value are from 20 % to 100 %.

4) The experimental results suggest that the command value have more influence on bias gain. That is the command value directly affects the sink flow, and restricts the displacement range of dual-valve EHES.

5) The excitation parameters should be properly matched to reduce sink flow influence.

References

Saton N. Frequency characteristics of electro-hydraulic vibrator. Journal of UOEH, Vol. 24, Issue 4, 2002, p. 405-412.

Publisher
Ghafari S. H., Golnaraghi F., Ismail F. Effect of localized faults on chaotic vibration of rolling element bearings. Nonlinear Dynamics, Vol. 53, 2008, p. 287-301.

Publisher
Han D., Gong G. F., Yang H. Y., et al. Waveforms analysis and optimization of new electro-hydraulic excitation technology. Journal of Central South University, Vol. 21, 2014, p. 3098-3106.

Publisher
Zhang J. Z., Guan L. Z., Li K. K. Study on high frequency hydraulic exciter based on rotary valve control. Advanced Materials Research, Vol. 490, Issue 495, 2012, p. 1441-1445.

Publisher
Lian H. Z., Kou Z. M. Characteristics analysis and development summary on hydraulic exciting ways of vibrating machine. Coal Mine Machinery, Vol. 27, Issue 11, 2007, p. 12-14.

Search CrossRef
Wang S. H., Tsung T. T., Han L. L. Hydraulic square-wave pressure generator with a specific rotating valve. Measurement, Vol. 42, 2009, p. 672-677.

Publisher
Liu Y., Gong G. F., Yang H. Y., et al. Mechanism of electro-hydraulic exciter for new tamping device. Journal of Central South University, Vol. 21, 2014, p. 511-520.

Publisher
Ruan J., Burton R. T. An electrohydraulic vibration exciter using a two-dimensional valve. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 223, 2009, p. 135-147.

Publisher
Yu J., Zhuang J., Yu D. H. State feedback integral control for a rotary direct drive servo valve using a Lyapunov function approach. ISA Transactions, Vol. 54, 2015, p. 207-217.

Publisher
Kyoung K. A., Quang T. D. Self-tuning of quantitative feedback theory for force control of an electro-hydraulic test machine. Control Engineering Practice, Vol. 17, 2009, p. 1291-1306.

Publisher
Guan G. F., Cong D. C., Han J. W., et al. Application of FRF estimator based on errors-in-variables model in multi-input multi-output vibration control system. Chinese Journal of Mechanical Engineering, Vol. 4, Issue 20, 2007, p. 101-105.

Publisher
Weng F. L., Mao W. J. Parameter-dependent vibration-attenuation controller design for electro-hydraulic actuated linear structural systems. Earthquake Engineering and Engineering Vibration, Vol. 11, 2012, p. 73-82.

Publisher
Peng Y. G., Wang J., Wei W. Model predictive control of servo motor driven constant pump hydraulic system in injection molding process based on neurodynamic optimization. Journal of Zhejiang University – Science C (Computers and Electronics), Vol. 15, Issue 2, 2014, p. 139-146.

Publisher
Jia W. A., Ruan J., Ren Y. Separate control of high frequency electro-hydraulic vibration exciter. Chinese Journal of Mechanical Engineering, Vol. 2, Issue 24, 2011, p. 293-302.

Publisher
Jarosław K., Marek S., Waldemar R. The control system for a vibration exciter. Solid State Phenomena, Vol. 198, 2013, p. 600-605.

Publisher
Marko Š., Mihael D., Niko H. Modelling of hydraulic spool-valves with specially designed metering edges. Strojniški Vestnik – Journal of Mechanical Engineering, Vol. 60, Issue 2, 2014, p. 77-83.

Publisher
Han D., Gong G. F., Liu Y. AMESim based numerical analysis for electrohydraulic exciter applied on new tamper. Applied Mechanics and Materials, Vols. 190-191, 2012, p. 11-18.

Publisher
Wei X. Y., Kou Z. M., Lu Z. R. Analysis on the pressure fluctuation law of a hydraulic exciting system with a wave-exciter. International Journal of Plant Engineering and Management, Vol. 4, Issue 16, 2011, p. 208-214.

Search CrossRef
Kou Z. M., Zhang H. X., Wu J., et al. Numerical simulation and experimental analysis of an active hydraulic excitation system based on pulsating flow. Advanced Materials Research, Vols. 295-297, 2011, p. 2216-2222.

Publisher
Ren Y., Ruan J., Jia W. A. Output waveform analysis of an electro-hydraulic vibrator controlled by the multiple valves. Chinese Journal of Mechanical Engineering, Vol. 1, Issue 27, 2014, p. 186-197.

Publisher
Chiang M. H., Lin H. T. The leveling position control of a four-axial active pneumatic isolation system using PWM-driving parallel dual-on/off valves. Applied Mechanics and Materials, Vols. 110-116, 2012, p. 3176-3183.

Publisher

Cited by

Dual-valve parallel prediction control for an electro-hydraulic servo system

Shi-jie Su | Yuan-yuan Zhu | Cun-jun Li | Wen-xian Tang | Hai-rong Wang

(2020)

Experimental Study on the Performance of Hydraulic Vibration Assisted Broaching (HVAB) Based on Piezoelectric Sensors

Zhen Meng | Jing Ni | Yu Shi | Chuan-Yu Wu | Xiang-Qi Liu

(2018)

About this article

Received

28 October 2015

Accepted

18 January 2016

Published

15 May 2016

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/jve.2016.16589

Keywords

dual-valve EHES

vibration exciter

effect of sink flow

amplitude gain

Acknowledgements

This research was supported by the National Natural Science Foundation of China (Grant No. 51375129), the 521 Talent Training Program of Zhejiang Sci-Tech University.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 08 01

Effect of excitation vibration on mechanical property and stress corrosion resistance of cast steel

Ruiying Shao, Hongjun Wang, Kunyan Lu, Juan Song

Research article

2019 03 31

Self-synchronization features of inertial vibration exciters in two-mass system

Grigory Panovko, Alexander Shokhin

Research article

2018 03 31

A more accurate dynamic model for dual-side excitation large vibrating screens

Liping Peng, Runxin Fang, Huihui Feng, Lei Zhang, Wenda Ma, Xiaodi He

Research article

2017 08 15

Double synchronization states of two exciters with horizontal asymmetric structure in a vibrating system

Lingxuan Li, Xiaozhe Chen

Z. Meng, C.- Wu, and J. Ni, “Effect of sink flow on dual-valve electro-hydraulic excitation system,” Journal of Vibroengineering, Vol. 18, No. 3, pp. 1563–1572, May 2016, https://doi.org/10.21595/jve.2016.16589

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16589
UR  - https://doi.org/10.21595/jve.2016.16589
TI  - Effect of sink flow on dual-valve electro-hydraulic excitation system
T2  - Journal of Vibroengineering
AU  - Wu, Chuan-yu
AU  - Ni, Jing
AU  - Meng, Zhen
PY  - 2016
DA  - 2016/05/15
PB  - JVE International Ltd.
SP  - 1563-1572
IS  - 3
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Wu_2016,
	doi = {10.21595/jve.2016.16589},
	url = {https://doi.org/10.21595/jve.2016.16589},
	year = 2016,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {3},
	pages = {1563--1572},
	author = {Chuan-yu Wu and Jing Ni and Zhen Meng},
	title = {Effect of sink flow on dual-valve electro-hydraulic excitation system},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]C. Wu, J. Ni, and Z. Meng, “Effect of sink flow on dual-valve electro-hydraulic excitation system,” Journal of Vibroengineering, vol. 18, no. 3, pp. 1563–1572, May 2016, doi: 10.21595/jve.2016.16589.

Copy IEEE

Copied to clipboard!

Wu, Chuan-yu, Jing Ni, and Zhen Meng. “Effect of Sink Flow on Dual-Valve Electro-Hydraulic Excitation System.” Journal of Vibroengineering 18, no. 3 (May 15, 2016): 1563–72. https://doi.org/10.21595/jve.2016.16589.

Copy Chicago

Copied to clipboard!

Effect of sink flow on dual-valve electro-hydraulic excitation system

Abstract

1. Introduction

2. Dual-valve EHES model

2.1. Valve port flow

2.2. Sink flow model

2.3. Dual-valve coupling model

3. Simulation and experiment

3.1. Simulation test

3.2. Experimental test

4. Results and discussion

5. Conclusion

References

Cited by

About this article

Related Articles